基于遗传算法和克里金的气温站网拓展设计

2020-06-06王佐鹏张颖超

科学技术与工程 2020年12期

王佐鹏,张颖超,2*,熊雄,潘霄,陈昕

(1.南京信息工程大学自动化学院，南京 210044；2.南京信息工程大学气象灾害预报预警与评估协同创新中心,南京 210044)

气温站用来提供准确的气温数据，是众多气象要素中的基础，并能对其他气象数据进行协同订正，最佳的站网可以更加准确地估算无站点位置的气温数据，所提供的信息可以用于各种领域，如农业、交通、环境学和生态学。因此最经济实用的气温站点布局是通过最少的站点数目，并能准确地预估无站点区域的气温，尽可能地降低估计误差。研究表明增加区域的站点密度可以减少估计的误差，但是更多的站点意味着更多的安装和监控成本。因此设计气温站网的目的是能够选择合适的站点数目和站点位置，以便能经济地提供准确的气象信息。

自2001年起，美国开始设计并筹建高精度气候变化的美国气候基准站网，于2008年建设完成美国本土114个站点的建设，满足未来50～100年美国国家级气候检测需求[1]。在中国，岑思弦等[2]利用旋转经验正交函数和结构函数对四川省降水场进行研究，推断出四川7个区域各自合理的布站间距；唐慧强等[3]利用结构函数结合支持向量机(SVM)等方法对长江中下游地区进行布站设计，该设计在考虑站点间距的同时利用SVM进行去除冗余站点。

近年来，统计学法、空间插值法、信息熵理论等已经被广泛应用在站网的评估和设计中。地统计空间插值法可以预估任何地点的数据[4]，其中克里金插值法是常用的空间插值法。克里金插值法是根据未知样点有限邻域内的若干已知样本点数据，在考虑了样本点的形状、大小和空间方位，与未知样点的相互空间位置关系，以及变异函数提供的结构信息之后，对未知样点进行的一种线性无偏最优估计[5]。目前，也有一些针对地统计学演变来的站点布局方法。Shaghaghian等[6]在2013第一次提出将地统计结合因子分析以及聚类技术进行雨量计布局设计；2017年，Xu等[7]通过克里金结合信息熵理论来针对雨量计的布局优化的方案。由于克里金法与其他估值法相比突出的优点是可以利用克里金方差提供估值精度，因此有勘探采样学者发现，新增勘探位置应选择克里金方差高的位置处，从而得到更多的勘探信息[8]。

根据中国气象局公布《国家地面天气站布局优化方案》，中国目前共有2 400多个国家级地面气象观测站，空间分辨率为71 km，但受制于观测要素、设备技术指标参差不齐等问题，其观测资料在中国数值预报业务中的同化应用非常有限，为此拓展国家级地面天气站网布局迫在眉睫，未来站点建在何处是亟待解决的问题。

为此，开发一种基于克里金插值法结合遗传算法的方法，利用现有站网的气象数据，寻找站点不足的区域，对该区域添加站点，最终的站网组合来满足未来站网的拓展要求。针对有多处站点不足的区域，且这些区域的局部最优之和不一定是整体最优的问题，具体来说就是添加两个及以上的站点时，不同的站点组合对未知区域的估值是不同的，所以这些局部最优的站点组合在一起，不一定就是未知区域预估最准确的的组合，如果使用彻底搜索来进行寻找，会导致计算量巨大，为引入智能寻优算法来替代彻底搜索站网组合的策略。结合地统计原理，利用分区域按比例随机选站法来分析整个区的克里金方差与站点数目之间的关系，降低离群站点带来的误差；通过现有站点与克里金方差之间的关系来确定遗传算法的目标函数的选择，以期为未来站点选址提供参考。

1 资料选取

江苏属于温带向亚热带的过渡性气候，气候温和，雨量适中，四季气候分明，是典型的东亚季风气候[9]。将江苏省58个国家级地面气象站点2016年日均温作为资料。

2 方法分析

2.1 克里金插值

克里金法是地统计学的主要内容之一，其在气象领域主要应用于日均值或更大时间尺度气象要素的空间预测与空间变异分析[10]。在众多克里金中，普通克里金(OK)是应用最广、最普遍的克里金方法之一，其公式可以定义为

(1)

式(1)中：z(x0)为未知站点的估计值；λi为已知站点的权重；z(xi)为站点的测量。权重λi通过变异函数进行求取，变异函数是用来表征随机变量的空间变异结构，是地质统计学的基础，其计算公式为

(2)

式(2)中：h为样点间隔距离;VAR为方差计算公式；z(x)与z(x+h)为区域化变量在空间位置x和x+h处的观测值。

在实际使用中，实验变异函数的计算方法为

(3)

式(3)中：γ*(h)为实验变异函数；N(h)为间隔距离为h的样本点对数；z(xi)与z(xi+h)为区域化变量z(x)在空间位置xi和xi+h处的观测值。常用的理论变异函数一般有球状、高斯和指数模型，一般根据拟合程度来选择理论变异函数,确定理论变异函数后已知站点xi对未知站点x0的权重λi可通过式(4)计算：

(4)

式(4)中：μ为拉格朗日常数；γ(xi-xj)为xi与xj之间的变异函数；γ(xj-x0)为xj与x0之间的变异函数值。

克里金方差为

(5)

作为衡量站网的评估因子，∂2(x0)可以反映站网最佳组合的性能。利用普通克里金法对研究域内其他未知区域值进行计算其克里金方差。比较克里金方差的大小，克里金方差越大表明所对应的位置上的估值越不准确。使用克里金方差旨在确定额外站点的区域，以最大限度地降低克里金方差。

2.2 遗传算法

遗传算法于1969年由Holland提出，是一种基于自然选择和生物遗传机制的随机搜索。通过模拟自然界中遗传，交叉和变异的现象，每次迭代保留一组候选解，并从中选择更好的个体[11]。通过遗传算子产生新一代候选解，并重复该过程直到满足群体适应水平。与其他启发式算法相比，遗传算法具有良好的全局搜索的能力、高效的搜索效率，使得求解参数不易陷入局部最优解，其基本流程如下。①设置最大迭代次数，设置初始种群内个体样本数目；② 计算种群中每个个体的适应度；③依据适应度选择高适应度的个体作为父母样本；④父母样本通过交叉、变异产生新的种群；⑤依次重复步骤②、③、④，直至最优解产生。

基于克里金和遗传算法开发的算法，由主要四个步骤组成(图1)：①通过现有的站点气温数据对整个区域进行空间变异性分析，确定克里金方差高值区域及其克里金估计值；②计算平均站点监测面积，确定站点数目；③通过分区域按比例随机选站法，确定目标函数；④利用遗传算法进行最佳站点选择，确定最优拓展站网布局。

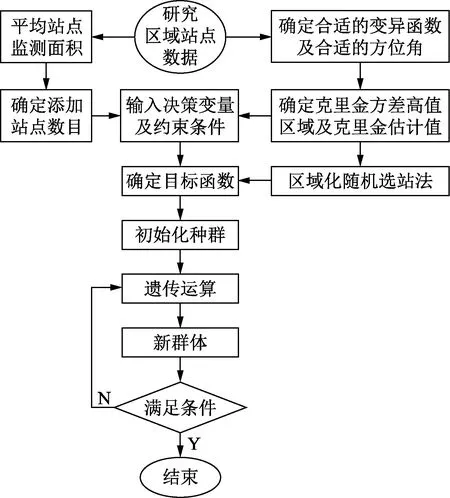
图1 站网设计流程图Fig.1 Station network design flow chart

3 实验分析

3.1 时间纬度选择

研究区域为江苏省58个国家地面气象站，站点位置信息如图2所示。

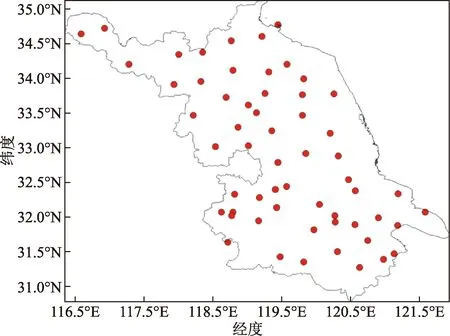
图2 站点分布Fig.2 Site distribution

研究资料的时间跨度为一年，为此选择合适的时间窗口对本研究方案也有一定的影响，所以对2016年12月31日的日均温、2016年12月的月均温、2016年下半年均温、2016年年均温这四个不同时间窗口进行克里金方差分析，研究其位置分布特征，其分布如图3所示。

图3 4个时间窗口的克里金方差分布Fig.3 The kriging variance distribution over four time periods

从图3中可以看出，选择不同时间窗口会导致克里金方差值的范围不一致，但是其位置分布情况基本一致，均呈现江苏省边界区域的克里金方差明显高于内部区域，这是因为江苏省周边区域的站点密度明显低于江苏省内部，特别是克里金方差越大的地方，站点密度越稀疏[12]，这也和前人对江苏气温插值法的研究得到的结论一致。因此时间窗口的选择对克里金方差的位置分布影响不大。时间尺度选择的越小，越能反应数据的真实情况，计算效果也最明显，所以选择江苏省2016年12月31日日均温做气温研究资料。

3.2 目标函数选取

目标函数的选择是整个设计关键，有两个克里金方差指标可以作为目标函数的选择，一个是平均克里金方差，一个是最大克里金方差，尽管这两个指标都和站点数目相关，但是各自的注重点不同，平均克里金方差在于表征一个区域的整体情况，而最大克里金方差在于表征这个区域中特殊个例。为了在最大克里金方差和平均克里金方差之中选择合适目标函数作为遗传算法的目标函数，所以就需要研究最大克里金方差和平均克里金方差分别与站点数目之间的联系。设计分区域按比例随机选站法来确定目标函数的选择，该方法既能够尽可能地降低由离群站点带来的干扰，使得算出的最大克里金方差和平均克里金方差更能准确地表征其与站点数目的关系，又可以降低计算量提高运行效率。该方法通过以下步骤来实现。

(1)利用现有的全部N个站点数据绘制研究区域的半变异函数以及各向异性曲线图，以此来选择拟合的变异函数模型和方位角进行切分研究区域。

(2)在切分后的区域按照比例法进行随机选择站点，使研究区域只有Ni(Ni≤N)个站点。

(3)重复1 000次步骤(2)，计算这1 000次的最大克里金方差的平均值、平均克里金方差的平均值作为最终的最大克里金方差Max、平均克里金方差Avg。

通过上述步骤对江苏2016年12月31日日均温进行分析。首先通过对江苏省内58个站点的日均温数据(2016年12月31日)进行半变异函数分析，以此来选择拟合的变异函数模型和方位角进行切分研究区域。块金系数Q=C0/(C0+C)，其中，C为偏基台值，C0为块金值，C0+C为基台值，块金系数可以反映空间相关性强度。当Q>0.75时，表示空间相关性很弱；当Q为0.25～0.75时，表示空间相关性中等；当Q<0.25时，表示空间相关性强烈。图4中，块金系数为

(6)

式(6)结果小于0.25，表明空间的自相关性强烈，根据克里金方差理论，以及江苏省2016年12月31日日均温与高斯模型的拟合优度r2为0.947，实验的克里金变异函数采用高斯模型。

图4 江苏省2016年12月31日日均温各向同性曲线Fig.4 Daily average isotropic curve of Jiangsu Province on December 31,2016

从图5中可以看出，气温的各向异性是不同的，从0°、45°、90°、135°四个方位来看，135°的空间相关性最好，基本呈现出与高斯模型一致的走势。因此以135°划分出来的两个区域中分别随机选择站点，最终组合起来的总站点出现不符合高斯模型的概率会低于对江苏区域整体进行随机选取站点，所以产生克里金方差更加贴近真实情况。

图5 江苏省2016年12月31日日均温各向异性曲线Fig.5 Daily average temperature anisotropy curve of Jiangsu Province on December 31,2016

因此将江苏省内全部的站点以135°线进行划分成2个区域如图6所示。所以在135°线上方有36个站点，135°线下方有22个站点。在对站点数目进行研究时，假设需要知道Ni个站点对应的最大克里金方差和平均克里金方差，其站点选取应当在135°线上方的区域选出36Ni/58个站点，135°线下方的区域选出22Ni/58个站点。由于在利用克里金插值的时候至少需要30个站点，因此对于Ni的初始值设定为30，并依次增加到58。最终结果如图7所示。

图6 135°方位角区域分割Fig.6 135° azimuth area segmentation

图7 克里金方差Fig.7 Kriging standard error

由图7可知，随着站点数目的增加最大克里金方差和平均克里金方差都在下降，但是平均克里金方差在随着站点数目的增加逐渐收敛，这表明从整体上而言，目前的站点数目已经满足对气温的监控，而最大克里金方差的下降趋势依旧明显，这表明对于个别特殊区域的监控能力弱，所以就现有站点位置而言对这些克里金方差高值区域的监控能力不足，需要对这些区域添加额外的站点，为此采用最大克里金方差作为目标函数更能反映这些特殊区域情况。所以遗传算法的目标函数选用最大克里金方差。

3.3 遗传算法参数设置

在确定目标函数后，添加站点数目可通过平均站点监控面积来确定，其公式为

(7)

式(7)中：m为克里金方差高值区域面积；M为研究区域的面积；n为站点数目。

对现有的58个站点进行克里金方差的计算并绘制在图8中。通过图8可以发现高值区域出现在江苏地图的边缘区域，将这些高于平均克里金方差，即高于0.35的区域选出来，当作克里金方差高值区域，即需要进行添加站点的候选区域。为此利用克里金插值法对这些区域进行模拟出气温数据，这样就拥有了候选区域的气温数据和位置信息。基于克里金方差的遗传寻优算法，其步骤如下。

(1)确定决策变量：决策变量就是克里金方差高于0.35的6个区域，即图8中黑色框线内选出来的区域内的站点位置。通过式(6)对这个6个区域进行站点数目确定，每个区域只要添加一个站点；最终决策变量为X1～X6各自位置信息。

(2)确立目标函数：分析可知将最大克里金方差作为目标函比较合理。克里金方差的公式为

(8)

式(8)中：x0表示需要预估的位置；μ为拉格朗日乘数；λi为每个站点的权重值；γ(x0-xi)表示每个站点到预估位置的变异函数模型值。因此最大克里金方差函数为F=max[∂2(x0)]，即目标函数。

(3)适应度数选择：确定出由目标函数值到个体适应度的转换，通过实际情况，需要评价个体适应度的最小值，即M=min(F)。

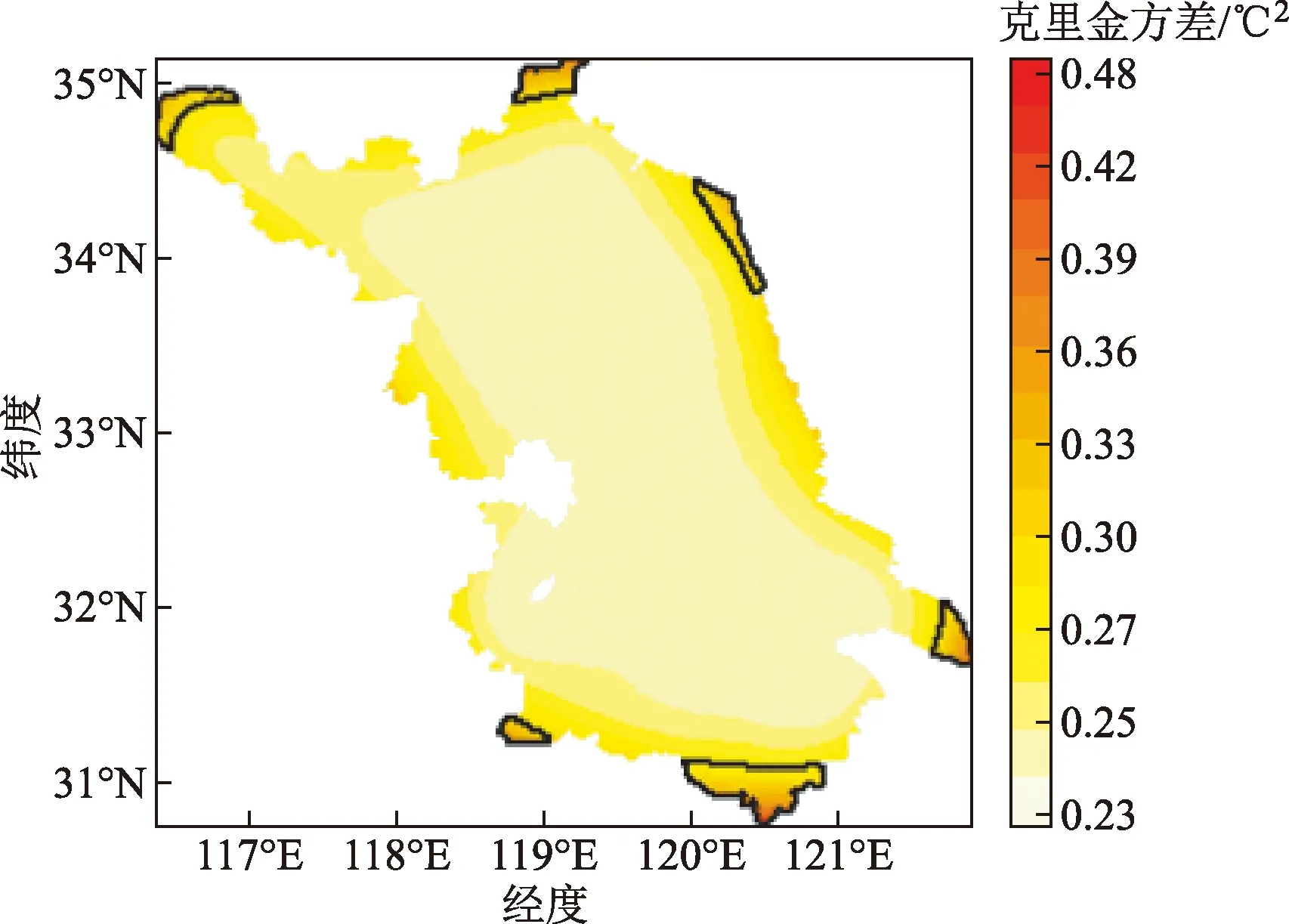
黑色框线内为候选区域图8 克里金方差及站点候选区域Fig.8 Kriging variance and site candidate area

4 对比验证

通过遗传算法自我迭代更新寻优后，最终获得了6个站点的位置，并且使该区域的最大方差降为0.331，该值远低于58个站点时的平均克里金方差。其站点位置以及添加站点后的方差如图9所示。最终这6个站点的位置信息如表1所示。

为了验证该方案的可靠性，做了四组对比试验，其中三组是在6个克里金方差高值区域随机选择6个站点位置，一组是在6个克里金方差高值区域选择6个最高克里金方差站点位置，结果如图10所示。

1～6为站点编号图9 站点位置及添加站点后克里金方差Fig.9 Site location and Kriging variance after site addition

表1 添加站点位置信息Table 1 Add site location information

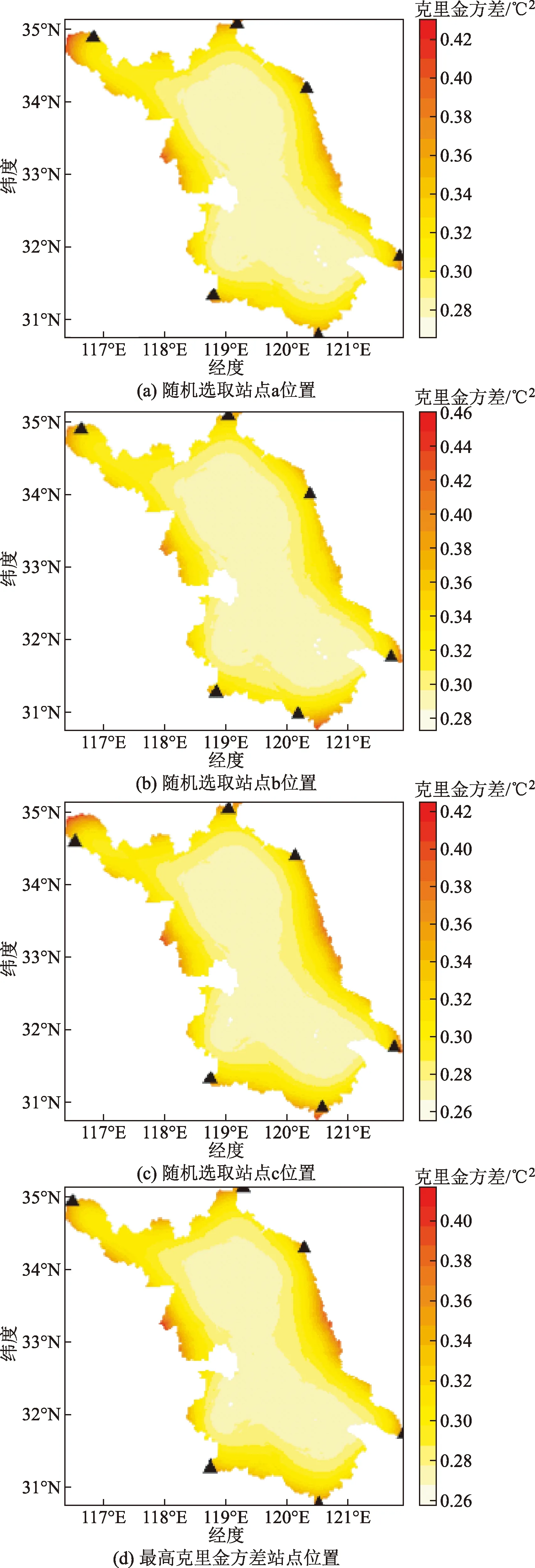
图10 对比试验Fig.10 Contrast experimen

由图10可知，四次对比试验的克里金方差的区间为(0.28，0.42)、(0.28，0.46)、(0.26，0.42)、(0.26，0.40)，而研究区域现有58个站点的克里金方差区间为(0.23，0.48)，可见随机添加6个站点确实能够降低最大克里金方差，但是不同的站点位置的组合会导致不同的克里金方差范围。通过遗传算法寻优出来的克里金方差区间为(0.231，0.331)，对比图10(d)将6个站点全部添加到克里金方差最大的位置，遗传算法寻优出来的结果更好。因此本设计在降低最大克里金方差的同时也间接地降低了整体的克里金方差，对于克里金而言，其估值的方法就是为了获取一个即无偏又使估计方差最小的值，所以能够导致更加准确的估计。