地铁隧道施工中钻爆强度对公路路基沉降的影响
2020-06-06于咏妍王稷良付重滔
于咏妍,王稷良,万 飞,付重滔
(1.交通运输部公路科学研究所,北京 100088;2.中铁十六局集团第一工程有限公司,北京 101300)
地铁隧道施工引起上覆土层的不均匀沉降,进而引发了公路路基的不均匀变形,形成了沉降槽。中国城市隧道施工过程中多用盾构法或浅埋暗挖法。因此施工对路基沉降影响的研究也多集中于此两种方法。
毛远凤等[1]研究了盾构法左右隧道先后施工引起的高速公路路面的位移;姚宣德等[2]研究了浅埋暗挖法地铁隧道施工对地表的沉降影响,提出地表控制值的建议;王仕传等[3]研究浅埋暗挖法的地下通道施工引起的沥青混凝土路面沉降及应力变化;刘泽贵[4]研究了地下通道施工对路面结构应力的影响;程兴新等[5]研究了高速公路路基沉降影响的路面破坏,并提出差异沉降控制标准。
近年来,随着青岛、大连、重庆等城市地铁的建造,钻爆法施工在这些具有“土岩组合”地质特点的城市有了较多的应用。现阶段钻爆法地铁隧道施工对周边环境影响的研究主要集中于施工对建筑物的影响或减振措施的采用。目前钻爆法地铁隧道施工对路基沉降的影响研究不足。漆泰岳等[6]研究了钻爆法地铁隧道施工对地表及建筑物沉降的影响;杨明新[7]定性阐述了钻爆法地铁隧道施工期路面坍塌原因及坍塌预防措施;于咏妍等[8]研究了爆破法地铁隧道施工期周边地下管道的力学响应;王海涛等[9]建立了钻爆法地铁隧道施工引发的地表沉降与地下管线经济损失的关系式;宋瑞城[10]研究了地铁隧道爆破施工对周边建筑物的安全影响;郑大榕[11]、薛里等[12]分别研究了南京和青岛地铁施工中爆破的控制措施;王栋等[13]通过对爆破波的衰减提出用数值模拟方法预测地铁隧道施工的爆破效应是可行的。
中国的地铁隧道的施工中,钻爆法施工的使用范围少于盾构法及浅埋暗挖法,对应的研究成果也相对较少。随着土岩组合地区地铁的修建,钻爆法的应用将不断增加。但现有钻爆法地铁隧道施工的研究主要集中在施工中对周边建筑物的影响及爆破强度的控制措施上,对钻爆法施工对公路路基影响的研究成果相对较少。在施工中爆破强度的变化对路基沉降影响较大,因此应对地铁隧道施工中爆破强度对路基沉降的影响规律进行研究,为土岩组合地区中地铁隧道施工过程中路基的沉降控制打基础。
以青岛地铁3号线的君峰路-西流庄区间(君-西区间)隧道施工为工程背景,以FLAC3D软件模拟钻爆法地铁隧道开挖。讨论地铁隧道施工过程中不同爆破强度对路基的沉降影响。
1 建模说明
1.1 计算模型
1.1.1 模型选取
选取君-西区间的K21+710断面建模分析。此区间断面采用上下台阶法施工,断面围岩为Ⅳ级。根据断面实际情况考虑合理的简化方式,在模型中地铁隧道尺寸简化为宽度6.3 m,高度6.6 m断面。模型尺寸考虑为上边界选取到地表,下边界距离隧道边缘为3倍隧道宽度处,左右边界距离隧道边缘为2.5倍隧道宽度。即隧道拱顶距离地表为 11.4 m,左右边界距离隧道约16 m,下边界距隧道20 m。模型尺寸取为高38 m,宽38 m,隧道开挖方向取为18 m,如图1所示。
模型中需要施加爆破荷载,因此模型采用自由场边界条件。隧道周边岩土体采用M-C本构关系[14]。
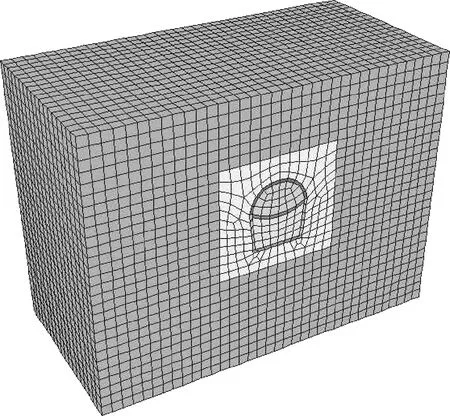
图1 计算模型图Fig.1 Calculation mode
1.1.2 边界条件
数值模拟计算过程分为静力分析和动力分析两部分。静力分析过程中,模型四周边界条件设置为水平位移约束,模型底部边界设置为固定端约束,模型上表面为地表设置自由边界条件,在重力荷载作用下进行收敛计算。动力分析过程中,将在模型中需要施加爆破荷载。如采用静力场边界,则需要模型尺寸庞大影响计算速度。因此去除静力边界条件,模型四周及底部采用自由场边界条件。
1.1.3 监测点布设
利用FLAC3D软件监测隧道断面开挖过程中,路基处x、y、z三个方向的位移变化。在隧道爆破开挖过程中,开挖区域上方路基沉降幅度变化大,远离开挖区域路基沉降变化较小。因此在进行路基沉降监测点布置时,以隧道中心线为轴,左右两端各17 m范围内,对称布设监测点。其中隧道中心线位置,及其左右两侧各1 m布设监测点,后续3~17 m范围内,每隔2 m布设一个监测点。软件监测数据与现场监测数据进行对比,以判断数值模拟中参数选择的正确性。同时比较不同工况下的路基沉降监测数据,获得钻爆法施工中路基沉降的变化规律。
1.2 材料参数
君西区间岩土层主要包含填土、黏性土、粗砂、强风化花岗岩、中风化花岗岩等。研究断面处由地质勘察所得的各层岩土体物理力学参数如表1所示。衬砌选用C30混凝土。
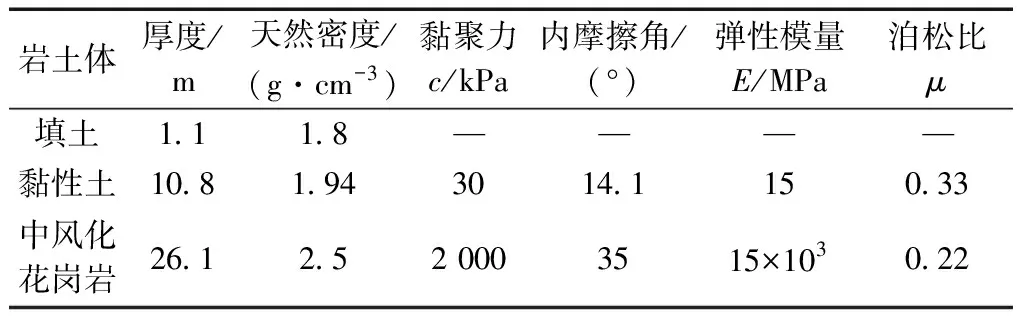
表1 数值模拟中围岩物理力学参数Table 1 Physico-mechanical parameters of soil stratum in mode
研究中不考虑锚杆、格栅钢架、及注浆小导管的受力变化。因此,根据面积等效原则进行相应简化,分别调整隧道周围岩体参数。
1.3 爆破荷载的施加
1.3.1 爆破的荷载的输入
研究中爆破荷载的主要施加方式分为施加监测波及施加模型简化波两类。监测波能更好地反映现场实际情况,但只针对于特定区间内。且在研究中将考虑不同爆破强度下路基的沉降变化,施工中实际的监测波只能针对某一特定爆破强度。因此研究不采用监测波,而选用模型简化波施加爆破荷载。
采用爆破研究中常用的三角形脉冲波进行模型中爆破荷载的施加。如图2所示,三角形脉冲波中主要组成参数包括脉冲波荷载上升时间tr、脉冲波总作用时间ts及波形峰值Pmax。在模型中,通过式(1)~式(5)的计算,确定三角形脉冲波的主要参数,以fish语言将三角形脉冲波函数输入模型中,在模型中将爆破荷载以应力的形式施加于开挖面上。

图2 三角形脉冲波Fig.2 Triangular pulse wave
三角形脉冲波荷载上升时间tr(单位:s)及总作用时间ts(单位:s)计算公式分别为[15]
(1)
(2)
式中:K为岩体的体积模量,105Pa;μ为岩体泊松比;Q为炮眼装药量,若同时起爆,即为总药量;若延时起爆,即为单端最大药量,kg;r为距离,m。
青岛地区爆破荷载施加的研究成果表明,三角形脉冲波中,可采用荷载上升时间8~12 ms,荷载总作用时间0.08~0.12 s[16]。
青岛地铁隧道施工中基于控制地表振速来保证爆破施工的安全。因此在三角形脉冲波的波形峰值确定中,将以地表振速最大值来反算脉冲波峰值。
根据萨道夫斯基公式[式(3)]、比例距离计算公式[式(4)]和荷载峰值计算公式[17][式(5)],结合青岛地区工程地质条件和振速峰值,可获得三角形脉冲波计算公式中的荷载峰值Pmax(单位:MPa)。
(3)
Z=R/Q1/3
(4)
(5)
式中:V为质点振动速度峰值,cm/s;K′为与爆破场地条件有关的衰减指数;Q为炸药量齐发爆破时取总装药量,分段起爆时取最大段装药量,kg;R为炮眼到荷载作用面的距离,取为爆破施加面到地表距离,m;α为与地质条件有关的衰减指数;Z为比例距离。
其中与爆破场地条件有关的衰减指数K′和与地质条件有关的衰减指数α取值如表2所示。

表2 爆破区K′、α值Table 2 Value of K′,α in blasting areas
1.3.2 阻尼比参数的确定
阻尼的产生主要来源于材料的内部摩擦以及可能存在的接触表面的滑动。FLAC3D在动力计算现提供了三种阻尼形式:瑞利阻尼、滞后阻尼、局部阻尼。
在阻尼形式中,瑞利阻尼由于其理论与常规动力分析方法类似,被大量研究者使用。瑞利阻尼用于动力计算中,可减弱系统的自然振动模式的振幅。相关实践证明,瑞利阻尼计算得到的加速度相应规律比较符合实际。但瑞利阻尼的不足是计算时间步较小,使动力计算时间延长。
滞后阻尼以模量衰减系数Ms来描述土体的非线性特征。与瑞利阻尼相比,它不影响动力计算的时间步。可以应用于任意的材料模型。但目前相关参考资料较少,在模型较为复杂时,不易得到满意的分析结果。因此研究不考虑滞后阻尼的使用。
局部阻尼在振动循环中通过在节点或结构单元节点上增加或减小质量的方法达到收敛,由于增加的单元质量和减小的相等,因此总体来说,系统保持质量守恒。局部阻尼系数αL的计算公式为
αL=πD
(6)
式(6)中:D为临界阻尼比,可以参考取为瑞利阻尼中的最小临界阻尼比ζmin。对于岩土材料,临界阻尼比ζmin一般为2%~5%,结构系统ζmin一般为 2%~10%。选择临界阻尼比ζmin=5%进行模型计算。
1.3.3 单元格尺寸控制
网格单元的尺寸不应大于波形最高频率对应的波长的1/8~1/10。在计算中,控制输入波的最高频率以防止波形的失真。
Δl=(1/8~1/10)λ
(7)
(8)
式中:Δl为沿着波传播方向的差分三角形网格单元的最大长度,m;λ为最短波长,即最高频率所对应的波长,m;c为纵波波速Cp和横波波速Cs中的小值。
当没有现场实测波速时,Cp、Cs计算公式为
(9)
(10)
式中:K为体积模量,GPa;G为剪切模量,GPa;ρ为岩体密度,kg/m3。考虑到君-西区间隧道穿行围岩以中风化花岗岩为主,因此在计算横波及纵波波速时选用相应的材料参数来计算。通过计算取单元格尺寸应控制在2 m以内,从而满足动荷载波形的要求。
2 爆破强度的控制
青岛地铁施工过程中,根据周围建筑物或构筑物的建造年代和重要性等因素控制振速,来保证建筑物或构筑物的安全性。由于在施工过程中,工程人员常根据地表振速峰值调整爆破用药量,因此爆破强度以振速峰值的大小进行描述。
研究所依托的青岛地铁君-西区间施工过程中,地表振速峰值控制为2.0 cm/s。在青岛地铁施工过程中,地表振速最大值常被控制在1~2 cm/s。部分施工区域,如永平路-青岛北站区间,考虑到其特殊性,控制地表振速在0.5 cm/s内。
研究中振速的取值范围将综合考虑青岛地铁施工常用控制值、相类似工程中实测值和各地区规范常用数值。
2.1 振速实测值
表3统计了多个地铁爆破工程施工过程中振速最大值。工程背景主要集中在青岛、广州、重庆、南京、深圳、武汉。振速统计值主要集中在地表处,但其中部分工程的爆破振速监测选择在建筑物的室内外地面。

表3 中国爆破开挖地铁隧道实测振速统计Table 3 Statistics on vibration speed of blasting subway tunnel in China
续表3

工程振速最大值/(cm·s-1)深圳地铁二十标区间隧道SSK4+046地表2.14武汉地铁二号地表1.94武汉地铁二号广虎区DK23+760地表2.84武汉地铁2号线地表1.9青岛胶州湾海底隧道地表1.42重庆市轨道交通一号线(大坪站-石油路站)地表1.5~2.0
由表3可知,青岛地铁隧道钻爆法开挖时,实测地表振速主要集中在1.5~2.5 cm/s。大部分地区地铁施工中,地表振速均控制在3.0 cm/s以内。部分地区振速峰值达到5.3 cm/s。
2.2 振速控制值
中国地铁爆破施工过程中,常根据施工区域周边的建筑物的使用性及安全性角度来控制振速值。《爆破安全规程》中注明保证建筑物安全运营情况下,爆破振动速度应控制在5.0 cm/s以下。根据房屋结构抗震能力建筑物安全振动速度控制在2.0~5.0 cm/s。《城市轨道交通安全保护第三方监控量测指标》控制由于打桩振动、爆破振动引起的峰值速度应控制在2.5 cm/s以下(对连续性的振动控制应按50%甚至更为严格控制)。因此结合两个标准,考虑建筑物的安全性,对比模型中的爆破振动峰值速度应控制≤ 2.5 cm/s。
而从环境角度考虑,在人口稠密的市区进行地下爆破,当爆破振速达到0.5~2.5 cm/s时,人会有不舒适感。因此,考虑人的舒适感,对比模型中爆破振动峰值速度应控制≤2.5 cm/s。
香港对于质点最大振动速度(PPV)控制值除考虑爆破点距已建成结构的距离外,还考虑爆破施工期间是否为交通高峰时期。常用爆破振速控制值为2.5~7.5 cm/s。其中考虑到周边存在的一般性建筑物和公用设施(如地下供水、排水管),爆破引起的最大振速控制在2.5 cm/s以内。
2.3 振速范围选取
综合考虑到中国地铁隧道爆破开挖过程中的振速监测值、相关规范的振速控制值,在对比模型中将选取地表振速最大值控制在 1.0~2.5 cm/s范围内。但在算例的实际计算过程中,发现当地表振速最大值达2.2 cm/s时,路基沉降最大值接近30 mm,即多地区施工中的路基沉降限值。其原因可能是,计算断面处的中风化花岗岩层与隧道拱顶距离较小。因此在对比模型中选取地表振速最大值控制在1.0~2.2 cm/s。其中标准模型将根据工程实际情况,控制振速最大值为2.0 cm/s。
3 模拟结果分析
3.1 标准模型分析
标准模型中选择振速为2 cm/s,以模拟区间的实际情况。
图3为隧道开挖完成后,隧道中轴线处及距离中轴线-4、-8 m处对应的路基的竖向、水平位移。

图3 隧道开挖完成后路基处位移Fig.3 Displacement on roadbed after tunneling
从图3可知,距离隧道中轴线0、-4、-8 m处对应的路基竖向位移峰值分别为24.17、18.66、7.69 mm。路基水平位移峰值分别为2.035×10-2、6.85、7.26 mm。随着距隧道轴线距离的增加路基水平位移有所增长,此种变化可认为施工过程中,隧道中轴线两侧的路基出现了向中间移动的现象。
因为在施工过程中主要监测路基的竖向位移,对水平位移监测的工程不多,不便通过对比监测结果与计算结果直接判定路基的水平位移计算准确性。并且通过对比发现,路基水平位移小于竖向位移,特别是位于隧道中轴线处对应的路基位移。因此不再讨论地铁隧道钻爆法施工对路基水平位移的影响。数值模拟结果将主要考虑路基的竖向位移值。
3.2 监测结果与标准模型对比
选取计算断面K21+710附近处,附近施工监测点布置示意如图4所示。从图4可知,计算断面K21+710附近布置位移监测点DC06-02~DC06-06、DC07-01~DC07-05。选取DC06竖向监测位移与数值模拟中计算位移进行对比,以判定计算模型的准确性。

图4 施工监测点布置Fig.4 Construction monitoring site
图5为标准模型计算所得路基的竖向位移与DC06监测所得的竖向位移的对比。从图5中可知,隧道中轴线处所对应的路基竖向沉降值,模型计算所得为24.17 mm,监测所得为26.33 mm。监测值略大于标准模型计算值。隧道中轴线两侧的路基沉降监测值与计算值相符程度较好。因此可认为标准模型的计算结果可靠。

图5 沉降的监测值与计算结果对比Fig 5 Comparison of monitoring and calculation results of settlement
3.3 不同爆破强度下路基位移
通过总结多地区的地铁钻爆法施工过程中振速监测值、中国相关规范设定的振速控制值,并考虑多地区对沉降限值的要求,确定地表振速峰值为1.0~2.2 cm/s。
经过计算可得到钻爆法施工中,振速在1.0~2.2 cm/s的路基横向沉降曲线,如图6所示。

图6 路基横向沉降曲线Fig.6 Horizontal settlement curve of roadbed
从图6可知,随着振速的增长,路基沉降值不断增加。振速峰值为1.0、1.4、1.8、2.0、2.2 cm/s时,路基沉降最大值分别为3.88、9.22、18.61、24.17、29.28 mm。
随着振速峰值的增加,路基沉降值增大的幅度有所提升。振速峰值从1.0 cm/s增大到1.4 cm/s过程中,沉降最大值增加5.34 mm。振速峰值从1.4 m/s增大到1.8 m/s过程中,沉降最大值增加了9.39 mm。振速峰值从1.8 cm/s增大到2.2 cm/s沉降最大值增加了10.67 mm。
从沉降数值方面可知,在振速峰值达到 2.2 cm/s 时,路基沉降最大值已接近多地区地铁施工中的路基沉降最大值控制值30 mm。
图7为不同爆破强度下路基纵向沉降曲线。由图7可知,振速峰值控制在1.0~1.8 cm/s时,路基最大竖向位移位于隧道的初始开挖面。当振速峰值达到2.0 cm/s以上时,隧道初始开挖面处的位移出现一定程度的上浮现象。并且随着振速峰值的提高,上浮程度变得更加明显。

图7 路基纵向沉降曲线Fig.7 Longitudinal settlement curve of roadbed
一些地区在地铁隧道施工过程中,利用限定路基最大斜率来确保施工安全。通过对图7所得数据进行计算可得最大斜率如表4所示。

表4 路基沉降最大斜率Table 4 Max slop ratio of roadbed settlement
从表4可知,随着振速峰值从1.0~2.2 cm/s范围内的增大,路基沉降的最大斜率增加,且斜率增长幅度增加。基于表4所得数据,得出最大斜率数值及其拟合曲线如图8所示。由图8可以看出,最大斜率呈现非线性增长。
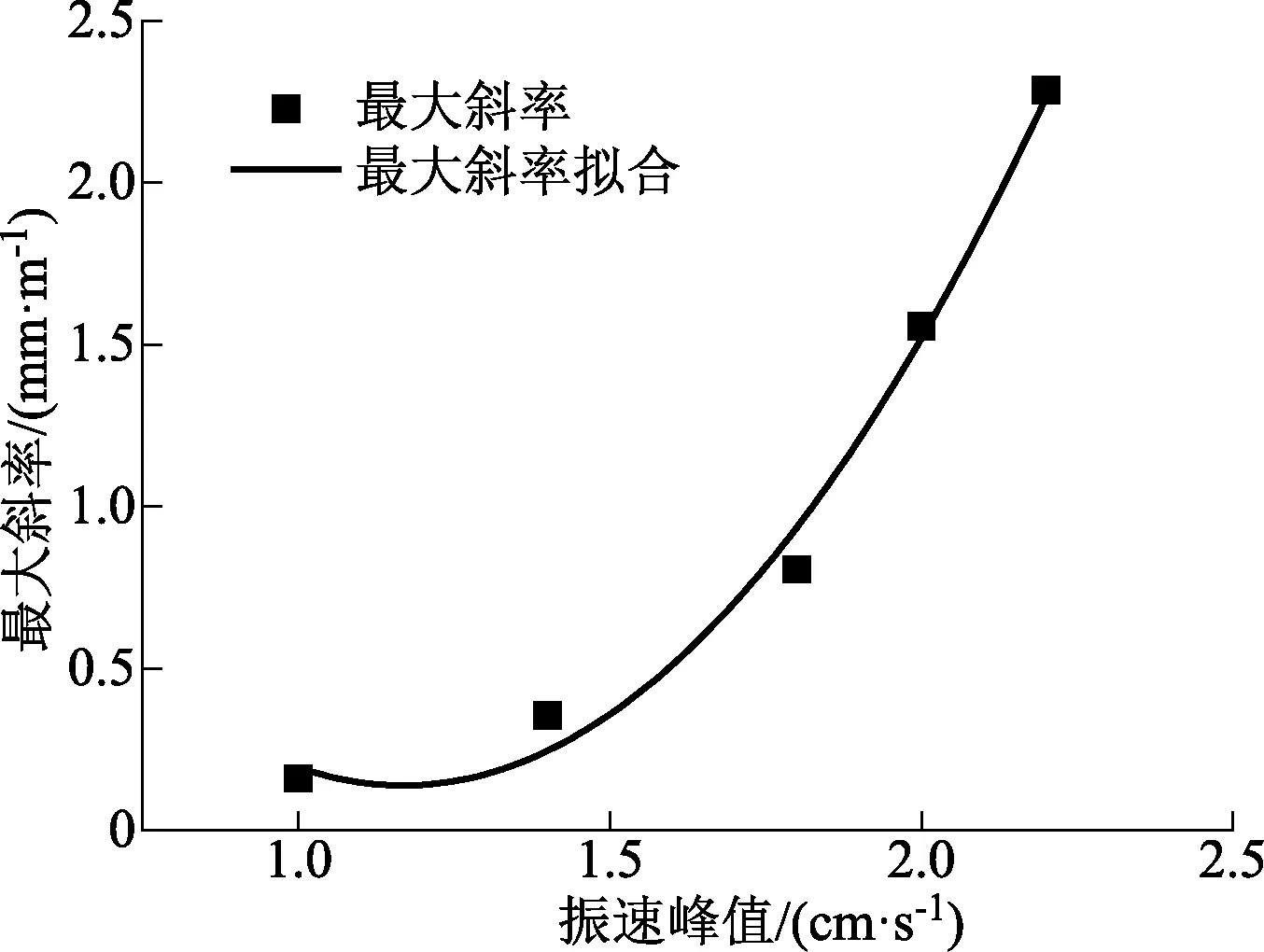
图8 最大斜率拟合Fig.8 Sloping ratio fitting of settlement
通过拟合,可得到振速峰值在1.0~2.2 cm/s时,路基沉降的最大斜率计算公式为
y=2.86-4.66x+2.00x2
(11)
式(11)中:y为路基最大竖向斜率, mm/m;x为振速峰值,m。
3.4 沉降槽分析
隧道施工中路基横向沉降曲线多符合Peck公式[式(12)][18-19 ],对计算所得路基沉降以Peck公式进行拟合。
(12)
式(12)中:S为横断面上与隧道轴线距离为x的路基沉降量;Smax为隧道中轴线处路基沉降最大值;i为沉降槽宽度系数,取沉降曲线反弯点与原点的距离;x为监测点距隧道中心线距离。
图9为计算所得的路基横向沉降槽曲线以Peck公式进行拟合。从图9可知,路基横向沉降槽曲线与Peck曲线拟合较好。可认为Peck拟合公式也可应用于土岩组合地区的隧道施工中。
由图9可知,路基沉降最大值随着振速增长而增加。但当距隧道中轴线17 m附近处,路基沉降值相差不大。
路基横向沉降槽曲线由Peck公式拟合后所得Smax及i如表5所示。
为求得钻爆法地铁隧道施工中,路基沉降曲线中重要参数的变化规律,分别研究路基沉降最大值Smax及沉降槽宽度i与振速峰值的关系。
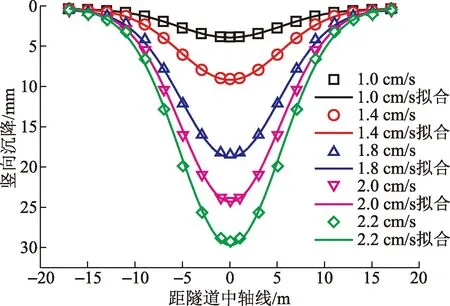
图9 路基的横向沉降槽Peck拟合Fig.9 Peck fitting of roadbed settlement

表5 拟合参数Table 5 Peck fitting parameters
图10为路基最大沉降Smax的拟合曲线。由图10可以看出,随着振速峰值的增高,路基最大沉降值Smax基本呈现线性增长。通过对路基最大沉降Smax进行拟合,得到路基最大沉降值及振速峰值的关系式。振速峰值在 1.0~2.2 cm/s时,路基沉降值最大值计算公式如式(13)所示:
y=21.9x-19.9
(13)
式(13)中:y为路基最大沉降,mm;x为振速峰值,cm/s。
从表5可知,随着振速峰值的增大,沉降槽宽度i的变化趋势并不明显。因此不再进行拟合分析。

图10 最大沉降变化趋势Fig.10 The changes of maximum settlement
4 结论
分析了钻爆法地铁隧道施工中,爆破强度对公路路基沉降的影响,并分析其沉降槽参数的变化规律。得到以下结论。
(1)随着振速峰值在1.0~2.2 cm/s增加,路基沉降不断增长。随着振速峰值的增加,路基沉降值增大的幅度有所提升。
(2)振速峰值在1.0~1.8 cm/s时,路基竖向沉降最大值位于隧道初始开挖面处,振速峰值达到2.0 cm/s后,初始开挖面处的路基竖向位移出现上浮。随着振速峰值的增大,路基竖向位移斜率不断增大,且斜率的增长速度加快。
(3)钻爆法地铁隧道开挖过程中,路基沉降曲线符合Peck公式,通过研究得到振速峰值在1.0~2.2 cm/s时,路基沉降最大值Smax的计算公式。随着振速的变化,沉降槽宽度i的变化规律并不明显。