基于信号小波预处理的继电保护仿真实验平台

于 群,毕 鹏,武传健

(1.山东科技大学电气与自动化工程学院， 青岛 266510； 2.北京交通大学电气工程学院， 北京 100044)

电力系统继电保护是电气学科的重要专业课，实践性、应用性、综合性较强[1]，教学过程中需结合实验。当前，多数高校电气专业的继电保护实验都是利用昂贵的仪器，通过设定好的故障数据来验证原理，实验教学的过程既不透明也无法灵活的模拟电力系统运行情况。由文献[2-3]提出的实验过程大部分建立在虚拟仪器或者数字仿真上，但是其难以与实际继电保护装置对接。文献[4-5]利用计算机仿真得到故障数据并且录波，但实验时必须使用有故障回放功能的继电保护测试仪。由加拿大研发的实时数字仿真系统(real time digital simulator，RTDS)作为一种高性能实时仿真平台，已经得到国际广泛认可[6-7]。RTDS虽逐渐在中国装机应用，但其价格昂贵，使用规程复杂，很多普通学校因经费不足无法购买。因此当前的继电保护实验设备无法满足普通高校教学的需要。

综合考虑动态模拟和经济实用的问题，提出一种基于MATLAB软件和高速数/模(digital/analog,D/A)转换硬件系统的继电保护教学实验平台，并运用小波理论对仿真信号进行预处理，以克服仿真算法引入的系统外误差。平台通过MATLAB强大的仿真建模以及程序控制能力，实时仿真电网正常和故障运行状态，仿真过程中可将其任一条线路电压电流通过高速数模转换模块输出，经功率放大后通入保护装置，期间获取保护装置的动作反馈信号，完成闭环测试实验[8]。学生和电气行业工作人员可以自由设置系统的参数、故障点以及故障类型，便于根据自身要求进行继电保护测试动模实验。

1 实验平台的硬件组成

1.1 实验平台的总体结构

实验平台硬件结构主要包括上位机MATLAB仿真平台、高速数模转换板卡、功率放大电路、采样前向通道、微机继电保护设备以及数字量IO模块。不同于传统继电保护实验仪器，设计的新型实验平台既包含实际物理装置实验，也拥有数字仿真功能，新型继电保护实验平台总体组成如图1所示。

UA、UB、UC、UN分别为A、B、C三相以及公共端电压；IA、IB、IC、IN分别为A、B、C三相以及公共端电流图1 实验平台硬件结构Fig.1 Hardware structure of the experimental platform

1.2 系统仿真平台

电力系统继电保护实验的仿真模型的建立是通过MATLAB/Simulink平台来实现的。Simulink是可以提供基本动态建模的软件环境，既能将具体环节的动态细节展示给使用者，又能清晰地展现各器件、系统之间的信息交换，体现各部分间的交互影响。仿真模型可依靠使用者自身仿真需求形成不同电压等级、不同运行方式的电网模型。

为使实验过程具有良好的可视化效果，仿真实验平台依据实验项目需要设计了用户界面，界面的搭建无须使用其他软件以及复杂的混合编程，通过在MATLAB图形用户界面(MATLAB GUI)中添加控件、编辑回调函数就可使实验平台用户操作界面完整清晰的展示实验项目，使用者在主界面单击不同的实验项目，可以进入不同的实验仿真模型中，进行模型和参数的设置。

1.3 数模转换模块

DA模块承接上位机软件仿真的数据结果，并转换为模拟量同步输出。转换过程通过高性能的DA板卡实现，选用Smacq公司开发的USB-5310高速模拟量输出卡。该款板卡基于USB总线，具有多路模拟信号转换通道。板卡波形输出的更新速率可以达到100 kS/s，同时该板卡的每个输出通道具有2 000字的先入先出缓存器(first input first output,FIFO)缓存，波形数据可以实现实时输出和多次重复实验。

数模转换板卡的主要特点如下。

(1)100 kS/s最大数字更新速率，可以实现100 kS/s的数据输出。

(2)支持多路模拟量同步输出。

(3)多种方式触发的实时波形输出。

(4)具有支持多种上位机编程语言调用的DLL-动态链接库，可以实现MATLAB、LABVIEW等软件对板卡的调用。

该板卡主要结构如图2所示。

图2 数模板卡主要结构Fig.2 Main structure of DA card

1.4 功率放大和信号调理电路

经高速数模转换输出的电压电流模拟量不能够带动大负载，进行实际保护装置的测试时，需要通过功率放大电路进行电压电流的放大。市场上的成套高压大电流功率放大系统大多价格昂贵，为此，采用分立式元件设计放大电路。

电压功放电路采用全对称差分输入将信号进行初步放大，中间放大级通过一对高压小功率管将输出电压放大到120 V，为使电流增大以提高功率，采用功率金属氧化物半导体场效应管(MOSFET)IRFP460，通过一对三极管驱动MOS管来增大电流，使MOS管处于甲乙类放大状态，以消除交越失真。功率放大输出MOS管的栅源极之间可加设限流保护支路，当电流过大可使栅源极信号减小，从而降低负载电流[9]。电压功率放大原理如图3所示。

Vin为输入电压；Vout为输出电压；R为电阻；D为二极管；GND为电线接地端；PNP为PNP型三极管；NPN为NPN型三极管；MOSFET为金属氧化物半导体场效应管图3 电压功率放大结构Fig.3 Voltage power amplifier structure

电流功率放大模块可以选用集成功放芯片OPA549来实现，通过多输出支路并联输出的形式可使电流放大到30 A以完成重载实验。输出信号经过电压形成回路反馈至输出端，将放大倍数稳定在一定范围。电流功率放大原理如图4所示，是2路电流并联输出。

Vf为反馈电压；Iout和Iout′为两路差分采样电流；C为电容；U1A、U2A为OPA549放大芯片；E/S为禁用和启用输出管脚；Ilim为电流输出限幅管脚；Ref为参考电位；U3A、U4A为UA741运放芯片图4 电流功率放大结构Fig.4 Current power amplifier structure

经过功率放大电路，电流和电压输出能够分别达到30 A和120 V，符合国家制定的电源发生器性能参数标准，可用于线路、变压器等测控装置的实际测试。电压电流放大电路的输出通过采样后进入DSP并与实际需求输出进行对比，保证放大的准确性和实验的安全[10]。

当保护实验现场不具备实际测试装置时，实验平台提供了以DSP28335为CPU(中央处理器)的微机保护主控板。教学实验过程中，可通过主控板进行继电保护原理以及判据的测试实验。实验时，DA输出的电压电流经由滤波电路、AD转换等，用来把模拟量转换为数字量传送到保护装置主控板CPU用于保护判据的验证。

1.5 数字量输入输出模块

为实现闭环测试实验的功能，实验平台采用多路数字量输入输出转换的形式收集开关量反馈信号。数字IO模块具有多路电平采集和转出通道，输入可达24 V。其作为继电器输出回路和上位机控制回路之间的连接器，将动作出口信号反馈至上位机。

2 实验平台的软件设计

区别于传统继电保护测试系统，新型实验平台将暂态计算、程序处理、数据格式和输出方式的控制全部交由上位机处理，下位机仅实现数据的接收和发送，随着计算机软件功能的日益丰富，以上位机为主的软硬件平台的控制模式将成为发展的新趋势。

2.1 实验平台的模型编辑

实验平台模型中的元件可从Simulink提供的元件库SimPowerSystems中直接使用，包括电源、分布式参数线路、负荷、变压器、三相故障模块、电压电流测量模块、电力系统图形用户截面Powergui等[11]。模型参数可按照实际系统算例设置，元件结构亦可根据实际选用。用户仅需要掌握软件的简单使用，便可完成电力系统仿真模型的搭建。

2.2 数据收集处理模块

平台的软件程序通过编写M函数实现，通过可视化的GUI界面展示各项软件功能。GUI操作界面使用户便捷的将运行仿真时所有的变量(时间、电压、电流)分类统计出来，使收集的各变量准确的反映电网运行时“正常-故障”的变化过程。在仿真模型中从正常运行到系统发生短路故障时的波形变化数据均以数组形式存于工作空间。根据对应电压等级、输出驱动负载种类的不同，将数据进行分类；对于不同的DA转换精度位数，也要进行相应的二进制转换。若输出的信号数组中峰值为Umax，每个数据点电压为Ui，Uo为输出电压，对应12位DA转换公式如式(1)所示：

(1)

对于不需转换为模拟量输出的数字仿真保护实验，可直接跳过数模转换步骤，另外输出前所有变量要经过小波检测。软件主程序流程如图5所示。

2.3 基于小波理论的信号重构方法

在MATLAB/Simulink中包含多种变步长数值解算方法，包括Ode45(显式四/五阶Runge-Kutta算法)、Ode23(显式二/三阶Runge-Kutta算法)、Ode23t(基于自由内插方法的梯形法)等，仿真时通过自动调整步长以适应变量的改变速度，以此来提高精度。不同仿真算法的迭代方式、仿真步长、误差限均有一定的差异，仿真算法的差异往往产生不同的数值结果。通过式(2)模拟算法的数值解差异。

(2)

式(2)中：y为函数自变量；x为关于变量y的状态变量；t为时间步长。用梯形法对式(2)两边积分，并整理为梯形面积的近似值求解：

(3)

将x(t-Δt)=0作为初始值，y的函数值从y(t-Δt)=0变化为y(t)=1，之后保持为1直到下个时间步长再次变为0。

求解t=0时刻的x(t)数值解，并且继续迭代，

(4)

(5)

x(t+2Δt)=0

(6)

不同仿真算法的解算过程中步长调整规则不同，若将y(t)变化较快的时间段由一个步长改为两个半步长，对应y(t)=0.5和y(t+Δt)=1，此时x(t)的数值解为

(7)

(8)

x(t+2Δt)=0

(9)

两种步长调整方式的部分求解结果如表1所示。可见其产生较大的数值差异，将求解结果采样后得到的仿真结果差异将更为明显，如图6所示。由图6可知，经过整时间步长采样后得到的仿真结果，在y(t)改变时产生了相异的数值解。

表1 部分求解结果Table 1 Partial solution results

图6 微分方程数值解差异Fig.6 Differences in numerical solutions of differential equations

实际进行仿真时，经常会出现由于断路器动作或是各种短路而引起的状态突变，不同的解法器在处理突变时刻的数值解时会产生较大的结果差别，给仿真实验带来影响。例如线路短路实验模型，采用双侧电源110 kV供电，线路AB和线路BC均为100 km，保护1和保护2分别安装在BC段线路和AB段线路的出口处。线路的正序阻抗Z1为0.4 Ω/km。故障示例和仿真模型如图7、图8所示。

图7中，A、B、C分别代表系统母线节点，保护1和保护2分别位于线路BC和线路AB的出口处，K点为模型故障位置。

图7 短路故障示例Fig.7 Short circuit fault example

图8 线路故障仿真模型Fig.8 Line fault simulation model

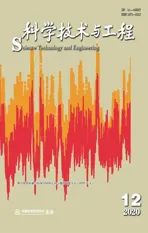
图7、图8中系统发生三相短路后A相电压如图9所示，在系统模型和参数不变的前提下，使用变阶数NDF(numerical differentiation formulas)法和梯形法求解的数值结果却产生了明显差别。

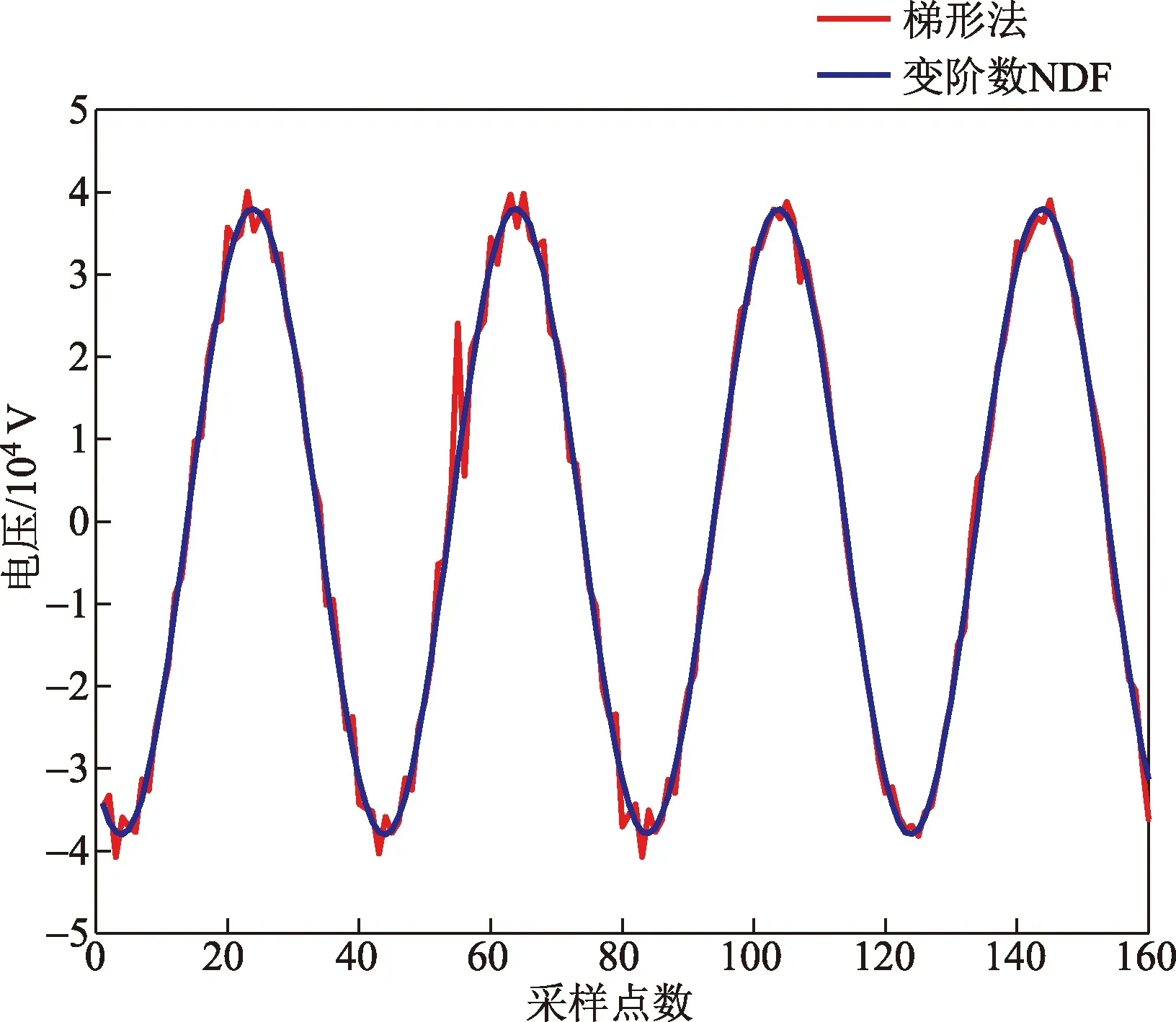
图9 线路A相电压Fig.9 A phase voltage of the line

取图9中一个工频周期计算其基波有效值，得到两种算法求解结果的50 Hz分量有效值分别为2.661×104、2.688×104V，其误差达到了1.01%，超出继电保护检测设备所要求的0.5%的误差限制。两种算法在该取样周期谐波畸变率分别为6.49%和0.85%，显然仿真结果的基波分量和各次谐波含量均出现较大差异。

建立变压器内部和外部故障仿真模型，如图10所示。

图10 变压器故障仿真模型Fig.10 Transformer fault simulation model

图9中两种算法在短路动作后的电流仿真波形如图11所示。图11中，两种算法求解的结果在网络模型改变时产生了明显的区别，图9中解算较稳定的变阶数NDF法在求解变压器模型时得到的电流波形出现了大幅值的持续振荡[12]；梯形法的表现却与之相反。可见教学实验过程中模拟量作为信号源输出时，算法间的差异造成输出信号之间的误差，干扰实验结果；较大幅值的瞬时量还会引发功放电路的过流保护截断输出，产生畸形的梯形波；长期工作在重载状态甚至会烧毁功率管，危害实验人员。所以在数字信号转为模拟量输出之前，应对信号进行检测和重构。

图11 两种算法求解的短路电流Fig.11 Short circuit current solved by two algorithms

检测的目的是为了寻找到数值突变的位置；重构则是为了尽量消除不同解法器数值结果之间的壁垒。由于不同解法器的迭代和计算过程的差异，其适用性依据求解对象的不同也具有一定差异，对于复杂多变的电力系统网络模型，难以在每次进行仿真前确定其最优解法器，而仿真时将常用的各种算法求解结果进行数值对比则会花费数倍仿真时间。因此，需要将不同解法器的数值解稳定在相应的标准，减小不同数值结果之间的误差，从而保证实验过程的高效和准确。

传统的低通滤波方法只能滤除波形中整段数据点的相应的频率范围，无法针对突变点处进行检测和处理；并且继电保护信号源需要具有一定的高次谐波输出能力(一般为2～19次)，所以低通滤波的截止频率选取较为困难。阈值去噪的方法在消除噪声干扰上的问题上效果良好，但仿真中出现的波形畸变是由解法器引入而非外界噪声干扰，该方法会将较大幅值的非源型误差视为有用信号从而失去对该点的滤波作用[13]，可见常见方法很难解决此类问题。因此，设计了基于小波理论的仿真信号检测与重构方法，利用小波算法的局部性检测优势，快速识别并且定位仿真结果中的信号奇异点，通过引入总谐波畸变率指标将高频含量较大的突变点系数进行不同处理，同时把突变点信息反馈给用户。该方法不但可消除瞬时大幅值突变量对后续模拟电路设计的影响，同时可在保留输出波形突变处暂态特征的前提下，降低不同解法器计算结果之间的各次频率分量的误差，有利于继电保护实验教学过程中对基波和谐波特征量的准确提取和计算。

小波分析作为一种新兴的数字信号处理方法，其最明显的优点是在时域和频域都有着良好的局部化性质，同时具有多分辨率分析的特点。由于其在信号处理上有着显著优势，小波分析在电力行业中的应用也越来越广泛[14]。

小波变换的定义如式(10)所示：

(10)

式(10)中：Wf(a,τ)为小波系数，是信号小波变换后的结果；ψ(t)为小波函数；a为尺度因子；τ为平移因子。重构公式为[15]

(11)

式(11)中：Cψ为小波基函数傅氏变换的条件，如果满足式(12)时，则ψ(t)为基本小波函数。

(12)

式(12)中：ψ(ω)为对应ψ(t)的像函数，ω为角频率。

选取Db5小波作为小波基函数，DbN小波拥有较好的正则性，信号重构过程比较光滑。小波变换分解的尺度根据不同信号的应用一般不同，实验平台输出重构方法的小波分解尺度一般为2～5。

对于信号突变位置的检测和重构来说，重要的一步就是利用模极大值来确定奇异点，即寻找到信号突变的位置。

∀δ>0, |x-x0|<δ

(13)

式(13)中：x为当前尺度信号的横坐标；x0为局部极值点；δ为任意实数。

当式(4)成立时，满足：

|Wjf(x)|<|Wjf(x0)|

(14)

式(14)中：|Wjf(x)|为尺度j上的模极大值；x0为小波变换对应的局部极值点，模极大值点对应的即为信号的突变点。用梯形法将一段线路的电压进行仿真计算，结果中出现许多较小数值突变信号，对波形做小波变换，如图12所示。

图12 信号小波变换结果Fig.12 Result of signal wavelet transform

图12中对原始信号S进行三尺度分解，d1、d2、d3依次为信号分解后的三层细节信号。在信号样本第32个数据点附近首次出现极大值点，由于细节信号的高频特性，原始信号高频分解系数的识别阈值Xset变得容易选取，可根据不同层次分解系数灵活整定。定位奇异点后，对于小于阈值的分解系数，可按照阈值去噪的方法将其舍去；对于高于阈值的小波系数，使用修正系数进行处理，为使重构后波形数据符合实际情况，引入总谐波畸变率指标(total harmonic distortion，THD)，根据《电磁兼容 试验和测量技术 供电系统及所连设备谐波、谐间波的测量和测量仪器导则》(GB/T 17626.7—2017)中，将THD定义为某次数下所有谐波分量方均根与基波方均根比值。

(15)

式(15)中：YH·h为h次谐波含量总和，分别取为电压和电流时，对应单位为V和A；THDγ为不大于某次特定高次谐波的总谐波畸变率，当用作继电保护实验信号源时，可取为20。系数识别阈值Xset由式(16)求得：

(16)

式(16)中：σ为信号的标准差;N为信号长度；j为对应的小波分解尺度。重构时引入修正系数α，其计算方法为

(17)

式(17)中：THDe为小波重构时的预期总谐波畸变率，取值参照各电网等级谐波标准。从第一层细节信号开始，将各层识别出的高频系数对应周期的系数经修正后再重构，达到预期THD时符合要求跳出子循环，否则继续下一层次高频信号的重构，其完整检测与处理流程如图13所示。

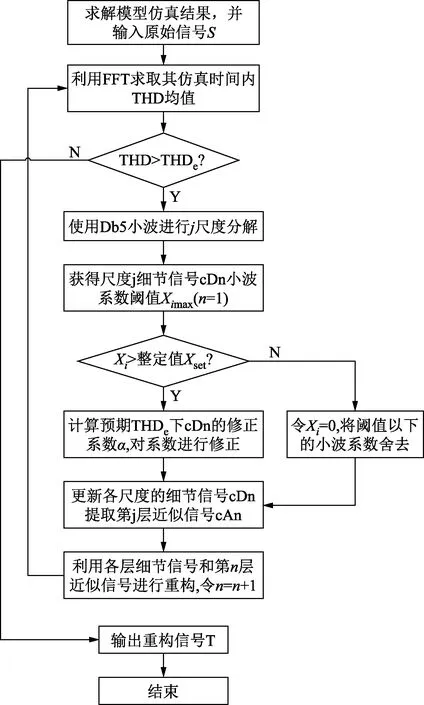
图13 信号重构流程Fig.13 Signal reconstruction process

2.4 方法对比和验证

原始信号S经过重构后，可消除不同算法在系统网络状态突变时产生的高频误差，其结果对比一般的滤波方法而言，这种方式显然更适合处理电力系统的仿真结果，结果如图14所示。

图14 三种处理方法结果对比Fig.14 Results comparison of three processing methods

图14为对原始信号采用三种方法预处理的结果，第一种方法采用低通滤波，由于继电保护设备采样时一般计及11次谐波，所以可将低通滤波截止频率设为600 Hz；第二种方法采用在信号分析领域应用广泛的小波阈值去噪，选取一维变量全局阈值进行去噪；第三种采用的处理方法。从图14可知，低通滤波效果一般，而阈值去噪方法会将数值计算的某些高频振荡视为有用信号从而无法实现降噪的目的；提出的重构方法相比以往方法降低数值计算误差效果显著。根据国标要求，取3 s内的电压总谐波畸变率平均值比较三种方法，如表2所示。

由表2可知，通过提出的小波预处理方法可有效降低谐波畸变率。将三种不同解法器仿真得到的原始电压信号S进行小波分解和重构，取某段周期重构前后的波形进行对比，如图15所示。

图15 重构前后电压波形Fig.15 Voltage waveform before and after reconstruction

图15中三种解法器重构前谐波含量具有较大差异，直接导致实验结果的不同，经重构后三种解法器求解的仿真结果之间的误差大大降低，且均符合电网实际运行时的相关要求，从而使信号输出具有了一定的标准。

将图15中三种解法器求解的数值结果重构前后的有效值和总谐波畸变率作对比，结果如表3所示。

三种解法器重构前的暂态时刻谐波含量较高，并且具有明显的差异；经重构后，解法器之间的暂态谐波之间的误差明显下降且周期有效值误差稳定在0.5%以内。取3 s内的平均电压总谐波畸变率，结果如表4所示。

表4 重构前后稳态电压谐波畸变率Table 4 Stable voltage THD before and after reconstruction

不同解法器求解结果的稳态期间谐波畸变情况经重构后明显改善，稳定在标准规定值内，且相互之间的差异显著降低。

3 继电保护教学实验算例

该实验平台输出的实时数据可以直接用于各种继电保护设备的测试，或用微机保护装置主控板直接进行教学实验。算例采用距离保护方式，通过微机保护的采样、故障判据和动作信号测试实验平台的教学实验功能。实验模型和相关参数采用图7的距离保护实验模型，相关整定值[16]如下。

保护2的第Ι段整定如式(18)所示：

(18)

式(18)中：Krel为可靠系数，一般取0.8～0.9；ZAB为线路AB段阻抗。

保护2的第Ⅱ段整定阻抗为

(19)

式(19)中：ZBC为线路BC的阻抗。

保护装置主控板的CPU选择DSP28335芯片，实验开始时电压电流模拟量经前向电路进入DSP的模数转换通道，微机保护的采样和计算采用傅里叶算法。实验结果的动作信号可由检测电路输出高低电平，经板卡IO功能读入返回计算机，完成闭环实验。

上位机模型设定故障时刻为0.100 s，类型为三相短路故障，并设置单侧电源供电时经10 Ω过渡电阻短路的情况，在未经过小波预处理的情况下输出数据；通过编程将傅里叶算法提取的电流电压有效值和相角进行计算并在上位机界面显示，得到不同短路点测量阻抗的值，如表5所示。表5对应的保护动作特性如图16所示。

表5 不同短路点的测量阻抗Table 5 Measured impedance at different short circuit points

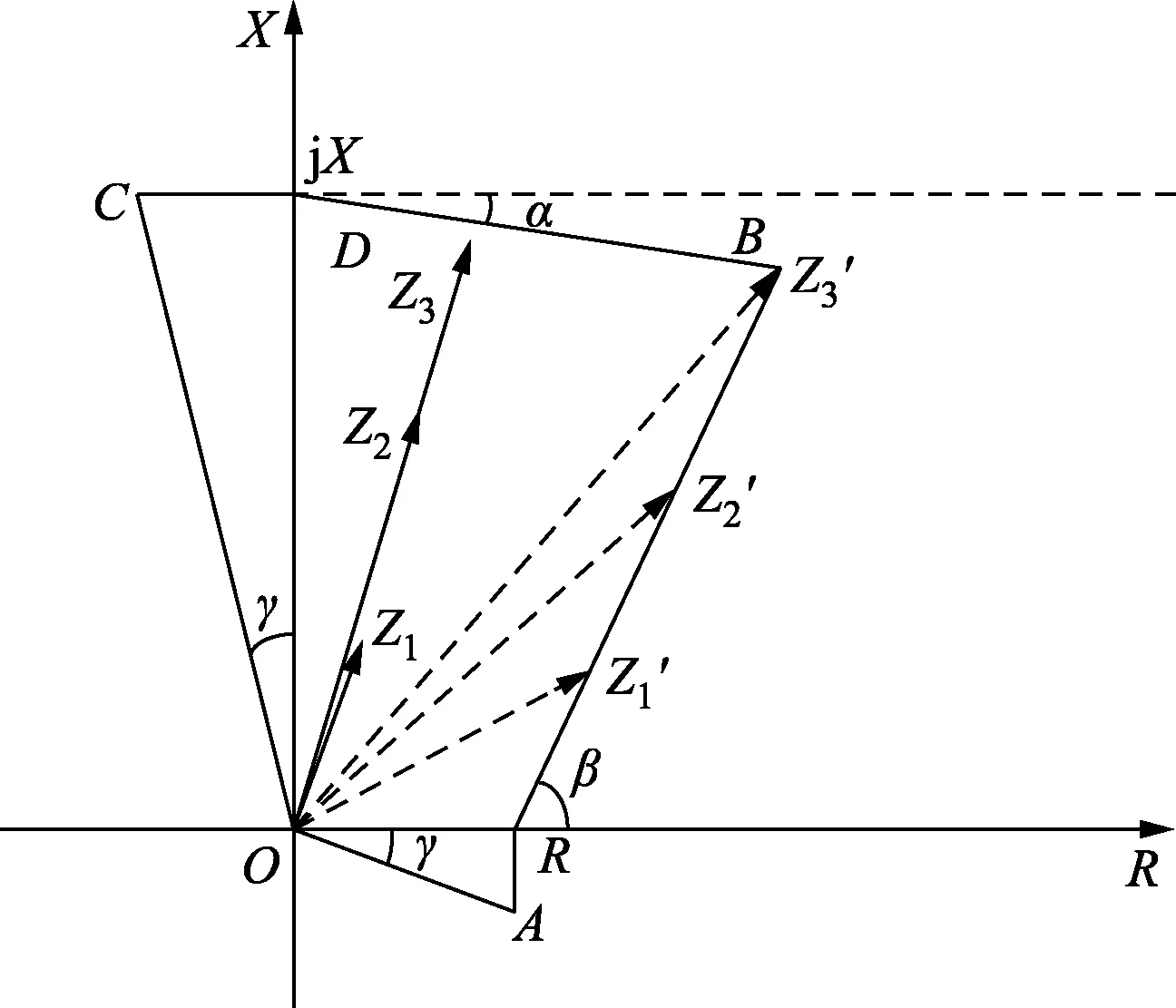
R、X分别为实数轴和虚数轴；Z为测量阻抗；A、B、C、D为保护动作范围的端点；α、 β、γ为整定边界夹角；R′和X′为未经过渡电阻短路时坐标图16 阻抗继电器的动作特性Fig.16 Performance characteristics of impedance relays

当短路故障位于保护末端时，测量阻抗落在整定区域边界处，此时若不同算法导致的数值结果误差较大时则会造成保护误动作，设置短路点距保护安装处85 km，重复多次实验。采用多种信号预处理方式进行数据预处理并测试，结果如表6所示。

表6 不同信号处理方法不正确动作次数对比Table 6 Comparison of incorrect operation times using different signal processing methods

显然，当不同的解算方法带来的数值计算误差较大时，动作区域边界的特性容易受到影响甚至产生不正确动作，但经小波预处理减小误差后得到的测量阻抗在保护范围内仍然动作，保证了实验结果的准确性。

通过实验平台可明显测得多边形特性的阻抗继电器能够承受较大过渡电阻的影响，且承受过渡电阻的能力和BR线的整定情况有关，起到继电保护教学的效果。

4 结论

针对现今继电保护实验的教学情况，结合近年来仿真实验平台的热点问题，给出了一种继电保护仿真实验平台的设计方案，并通过实际的微机继电保护装置验证了其可行性。

硬件系统利用计算机调控工业数据采集板卡，配合功放及辅助电路；软件功能的实现全部交由上位机软件处理，设计了小波循环检测与重构的信号预处理方式，保证教学实验内容的准确和实验过程的稳定高效。

与当前常用的RTDS等系统相比，的设计方案经济性强，易于实现，十分便于在电气行业的教学中使用和推广。