基于无迹粒子滤波的车辆质心侧偏角估计方法

张 征,马晓军,陈路明,刘春光

(陆军装甲兵学院陆战平台全电化技术重点实验室,北京 100072)

质心侧偏角是表征车辆运动状态的一个重要参数，准确获取质心侧偏角信息是进行车辆主动安全控制研究的基础[1-2]。对于大多数车辆，采用特定传感器直接测量质心侧偏角的成本很高，一般通过采集其他易于测量的状态参数信息对其进行间接估计[3]。

卡尔曼滤波(Kalman filter，KF)算法是一种应用较为广泛的质心侧偏角估计方法，但一些文献指出KF算法无法对非线性、非高斯噪声进行准确假定，在轮胎非线性阶段难以取得良好得估计效果[4-5]。为了更好地描述系统噪声，一些学者分别将无迹卡尔曼滤波(unscented Kalman filter，UKF)、粒子滤波(particle filter，PF)等算法应用于车辆状态参数估计系统[6]。文献[7-8]均采用UKF对四轮车辆质心侧偏角进行估计，研究结果表明UKF能够减小一部分由于模型线性化引起的误差，但UKF算法容易受到环境中的非高斯噪声干扰，影响估计效果。文献[9]运用PF算法进行车辆行驶状态参数估计，这种算法与其他滤波方法相比，能够更加准确地假定系统噪声，但PF算法存在粒子退化等问题，不利于工程应用。近年来，有学者提出了无迹粒子滤波(unscented particle filter，UPF)算法，UPF算法在PF基础上通过无迹变换(unscented transformation，UT)调整粒子分布，改善了粒子退化等问题，但UPF尚未完全扩展到分布式电驱动车辆状态参数估计系统中[10]。

轮毂驱动电动车辆作为分布式电驱动车辆的一种特殊类型，采用多个轮毂电机独立驱动，可以及时反馈驱动轮力矩、转速信号，便于在不增加额外传感器的情况下，设计合适的滤波器估测质心侧偏角[11-12]。将某型8×8轮毂电机驱动车辆作为研究对象，在双轨三自由度车辆模型的基础上，建立了车辆行驶状态参数估计方程，采集了易于测量的普通车载传感器信息和驾驶信号，设计了基于UKF算法的质心侧偏角估计器进行车辆状态参数估计。最后，利用MATLAB/Simulink和Adams进行了联合仿真实验，并开展了实车试验对估计方法的可靠性进行验证。

1 车辆动力学建模

轮毂电机驱动车辆行驶时，容易出现较频繁的加减速和转向运动，而常用的单轨二自由度模型一般难以满足车辆状态参数估计需求。为了适应研究对象复杂多变的越野机动环境，建立非线性三自由度车辆模型。所建模型如图1所示。

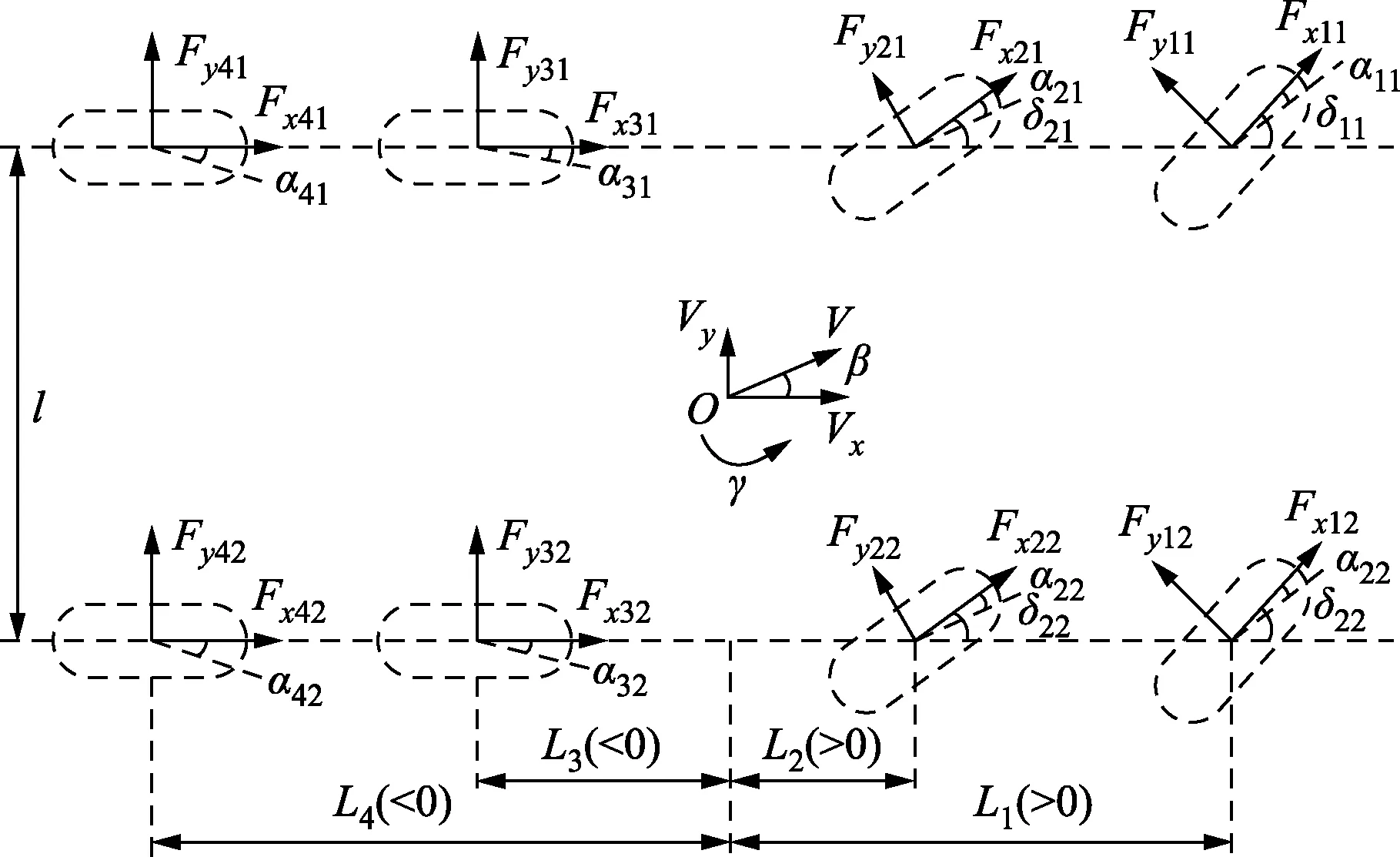
V为车辆速度；Vx和Vy分别为纵向车速和侧向车速；γ为横摆角速度；β为质心侧偏角；δij为车轮的转向角；αij为车轮的侧偏角；l为轮距；Li表示第i轴距离质心O处的距离；Fxij、Fyij分别为纵向力、侧向力(i=1，2，3，4表示第i轴；j=1，2表示左侧和右侧)图1 非线性三自由度车辆模型Fig.1 3-DOF nonlinear dynamics model of vehicle

建立车辆动力学方程：

(1)

将式(1)变化后，得到式(2)：

(2)

Fy21cos(β-δ21)+Fy22cos(β-δ22)-

Fx11sin(β-δ11)-Fx12sin(β-δ12)-

Fx21sin(β-δ21)-Fx22sin(β-δ22)+

(Fy31+Fy32+Fy41+Fy42)cosβ-

(Fx31+Fx32+Fx41+Fx42)sinβ]-γ

(3)

Fx12sinδ12)+L2(Fy21cosδ21+Fx21sinδ21+

Fy22cosδ22+Fx22sinδ22)+L3(Fy31+Fy32)+

Fx32+Fx42-Fx11cosδ11-Fx21cosδ21-Fx31-Fx41)]

(4)

轮胎纵向力Fxij计算如式(5)所示：

(5)

车辆侧向运动受到轮胎侧偏力的支配影响，因此需要构建能够反映轮毂电机驱动车辆非线性特性的轮胎模型，综合考虑建模的拟合精度和计算量，采用半经验公式的Pacejka轮胎模型，其一般形式为

Fy=Dsin(Carctan{Bα-E[Bα-arctan(Bα)]})

(6)

式(6)中：D为轮胎模型峰值系数；C为形状特性系数；B为刚度系数；E为曲率系数。

各轮侧偏角表达式为

(7)

2 质心侧偏角估计器设计

2.1 状态估计模型建立

建立车辆状态参数估计状态方程和量测方程

(8)

式(8)中：下标k和k+1分别表示k、k+1采样时刻；Xk+1和Xk分别为第k和k+1时刻状态变量；Yk+1为第k+1时刻量测变量；u为输入向量；wk、vk分别为零均值，且协方差为Q、R的过程噪声、量测噪声。

状态变量X=[βγVx]T，着重分析β的估计结果；输入向量u=[δijFxijFyij]T；量测变量Y=[axayγωij]T，其中，ωij为各车轮转速。

2.2 UPF算法设计

2.2.1 初始化滤波条件

(9)

2.2.2 递推滤波计算

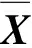
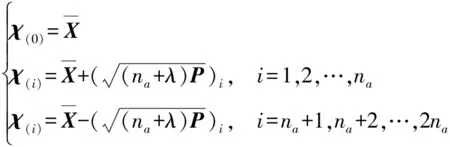
(10)

sigma点权值为

(11)

2.2.3 状态变量预测值及其误差协方差计算

对各粒子进行预测，sigma点预测值为

(12)

sigma点预测值加权后，X的预测值及其误差的协方差矩阵为

(13)

2.2.4 量测过程更新。

变换后的sigma点为

(14)

(15)

(16)

计算量测量协方差：

(17)

X与Y间的互协方差的关系可表示为

(18)

滤波增益为

Kk+1=P(X,Y)[P(X,Y)]-1

(19)

更新得:

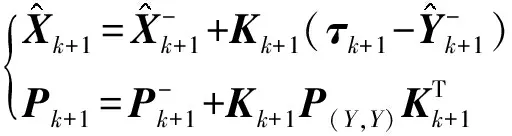
(20)

2.2.5 重要性采样

(21)

式(21)中：下标0:k-1、1:k代表第0～k-1、第1～k采样时刻。

新样本权值：

(22)

归一化得：

(23)

2.2.6 重采样判断

为了改善粒子退化情况，设定阈值Nt，并根据式(23)判断是否需要重采样

(24)

2.2.7 状态变量估计结果

UPF输出为

(25)

3 仿真结果及分析

利用MATLAB/Simulink和Adams进行联合仿真，实验工况设定为车辆在μ=0.8路面以初速度75 km/h进行蛇形行驶，实验参数取值如表1所示。

表1 车辆仿真部分参数Table 1 Parameters of vehicle simulation

为了检验UPF方法的估计效果，将UPF算法与较常用的PF算法进行对比，实验结果如图2、表2所示。

图2 高附着路面蛇形行驶工况Fig.2 Snake driving on high adhesion road

表2 蛇形工况下质心侧偏角估计误差Table 2 Estimation error of side-slip angle under snake driving

由图2可知，当路面条件较好时， PF算法和UPF算法均能对车辆质心侧偏角进行有效估计，但与UPF算法相比，PF算法的估计值与跟踪值间存在较大差异，尤其是当|β|较大时，估计误差更加明显。根据表2的估计误差统计数据可知，采用PF算法和UPF算法所产的最大误差分别为2.35×10-2、1.26×10-2rad，均方根误差分别为3.82×10-3、0.73×10-3rad，所设计的UPF算法估计精度更高。

4 实车试验

为进一步验证估计方法可靠性，基于某型8×8轮毂电机驱动车辆开展实车试验，试验设备如图3所示。设定工况为车辆在μ=0.4的路面以初速度40 km/h低速大半径转向行驶。试验结果如图3、表3所示。

根据图3、表3可知，当路面附着系数较低时，PF算法的质心侧偏角估计值和参考值的整体变化趋势相同，但当车辆侧向运动相对剧烈时，估计误差较大，最大误差达到1.38×10-2rad；UPF算法的质心侧偏角估计值能够非常准确地跟踪参考值，最大误差仅为0.62×10-2rad。另外，UPF算法和PF算法均方根误差分别为3.16×10-3、0.43×10-3rad，所以UPF算法的估计效果明显优于PF算法。

图3 低附着大半径转向行驶工况Fig.3 Large radius steering on high adhesion road

表3 低附着大半径转向工况下质心侧偏角估计误差Table 3 Estimation error of side-slip angle under large radius steering

5 结论

根据轮毂电机驱动车辆自身特点，对车辆行驶状态参数估计进行了研究，提出一种基于UPF的质心侧偏角估计方法。构建了非线性三自由度车辆模型，建立了车辆行驶状态参数估计方程，设计了关于车辆质心侧偏角的无迹粒子滤波估计器，并进行了联合仿真实验和实车试验。结果表明所提出的无迹粒子滤波估计方法在不同工况下均具有较强的适用性和鲁棒性，可以准确地估测车辆质心侧偏角。