爆破针型泄压装置力学行为模拟分析

2020-06-06蒋臧杰信志强

科学技术与工程 2020年12期

蒋臧杰,王磊,信志强

(河海大学力学与材料学院，南京 211100)

压力容器是泛指在一定的设计压力下运行的承压设备，在工作时能够承受的最大内部压力称为最高容许压力。压力容器在最高容许压力下能够安全运行，当内部压力超过其最高容许压力，压力容器的外壁有可能因为过高的压力产生过度塑性变形导致结构破坏，并造成严重的生产安全事故。安全泄压装置就是为了保证压力容器可以在最高容许压力下工作的一种安全保护装置。安全泄压装置要能够保证压力容器在正常运行状态下不泄漏，超压时泄放，防止压力容器出现超压工作状态，从而保证压力容器在工作时的安全。由于运行环境的复杂，安全泄压装置在承压设备运行时会出现各种各样的故障，如阀瓣开启过程中的颤振、阀门在临界泄放压力下出现泄漏、泄放量不足等[1-2]。安全泄压装置常用的材料为各类型结构钢，当阀门开启时，阀瓣在流体作用下会以高速冲击阀盖，即便是高强度的钢材，在阀瓣的多次冲击下依然会出现塑性变形乃至疲劳破坏。尤其是对于口径较大的阀门，阀瓣重量大。当入口压力较高时，阀瓣开启后速度逐渐增加，冲量会非常巨大。阀瓣受限制减速后，将会在极短的接触碰撞时间内对阀盖施加极大冲击力，可能直接造成阀盖的断裂破坏，阀杆与阀瓣冲出阀腔，进而造成严重后果。所以安全泄压装置在压力容器的安全工作中有着举足轻重的地位，具有非常实际的研究意义。

多年来，中外学者通过实验以及数值模拟方法对各型泄压装置进行了大量研究。郭崇志[3]通过贴应变片的方式，对安全阀的阀芯进行检测，将安全阀的参数检测集中在阀体本身的结构特性上，首次实现了安全阀的在线检测技术；丘垂育[4]通过实验研究了阀门在瞬态开启时阀瓣刚度对其性能参数的影响，指出柔性阀瓣能够提升阀门的性能参数，如提高泄放效率、提升阀瓣开启速度等相对于刚性阀瓣更具优势；Dossena等[5]通过实验方法研究了不同介质流体对阀门的性能参数、泄放系数等的影响，发现介质的比热容是最主要的影响因素；Stevenson等[6]运用Fluent软件对高压阀内流体的流动进行了可视化研究，通过对比数值模拟结果与实验结果，得出了数值模拟方法能够快速得到流场参数且数据准确的结论；梁寒雨[7]建立了安全阀的二维瞬态研究模型，通过瞬态模拟研究安全阀泄放过程中流场参数的变化，并取得一定的成果，得到了阀门入口段和密封段流场参数的变化特性。戴芳芳[8]对阀瓣和反冲盘所受的冲击力进行了研究，使用区域分解法实现了定量计算阀瓣及反冲盘的冲击力，并通过改变安全阀的结构参数如出入口直径、阀瓣尺寸等研究冲击力的影响因素。近年来，对于安全泄压装置的研究主要集中于超压泄放原理及泄压装置的性能参数的理论研究和工程应用这两方面。而随着计算机技术的发展，数值模拟方法成为理论研究的重要手段。通过泄压装置内部流场的数值模拟，研究内流场在安全泄压装置动态开启过程中的流动特性，如泄放量、开启速度、泄放系数等。因此无论是研发新型泄压装置抑或是对现有设备进行结构优化或者在线检测都离不开对泄压装置内部流场的理论或仿真分析。研究的某一型号的爆破针型泄压阀属于一种非重闭式泄压装置，该类型安全泄压装置在完成泄压动作后不会重新闭合。相较于一般弹簧式安全阀[9]和爆破片，这种爆破针型泄压阀具有显著的优势。随着中国石化工业和海洋油气的不断发展，爆破针型泄压阀在中国的应用也越来越普遍[10]。目前，美国机械工程师协会(American Society of Mechanical Engineers,ASME)锅炉及压力容器规范标准[11]已将爆破针型泄压阀列为可以采用的非重闭式泄压装置，而与之相对应的相关法规和标准均未涉及爆破针型泄压阀的设计与使用要求，如《压力容器》(GB 150—2011)[12]和《安全阀一般要求》(GB/T 12241—2005)[13]。该类型爆破针型泄压装置的国家标准还存在一定的空白，且目前未针对该种新型安全泄压装置性能参数和动态开启分析的数值模拟和试验研究。因此，通过计算流体动力学(computational fluid dynamics,CFD)数值仿真对爆破针型泄压装置的开启动态特性和性能参数以及阀盖在多次冲击循环下的疲劳分析进行的研究是十分必要的，以期通过的研究成果能够为该类型安全泄压装置的选型及结构优化提供一定指导。

1 数理模型与计算方法

有限体积法是计算流体动力学领域广泛应用的数值方法，相较于有限元和有限差分法，通过有限体积法得出的离散方程，要求因变量对任意一个控制体积都满足积分守恒，因而天然的满足整个计算区域的质量守恒定律。研究的爆破针型泄压阀具有阀门开度大，阀瓣行程长的特点，因此对其泄压过程的瞬态数值模拟需要能够实现网格的大尺度变形。阀瓣在泄放的初始阶段在流体介质作用下会产生向上运动的趋势，由于阀瓣的位移受爆破针的限制，此时爆破针会在阀瓣作用下产生微小的形变，阀瓣因此受到爆破针微小形变下产生的反力。通过CFD软件求解阀瓣在流体介质中所受流体力并结合通过用户定义函数(user-defined function，UDF)编写的爆破针的变形与反力的本构函数实现了阀瓣在流体介质和爆破针作用下的运动状态的数值模拟。爆破针型泄压阀典型结构如图1所示。

1为阀体；2为活塞式阀瓣；3为阀座；4为阀杆；5为阀盖；6为爆破针；7为针笼图1 爆破针型阀的典型结构[14]Fig.1 Typical structure of buckling pin valves[14]

爆破针型泄压阀的主要触发部件是爆破针，它是实现爆破针型泄压阀密封或泄压的关键部件。爆破针在阀门超压泄放时仅承受轴向压缩荷载，根据压杆失稳的欧拉定律[15]，当承受的轴向载荷F小于爆破针的临界载荷Fcr时，爆破针可以维持直线平衡状态。当轴向载荷F达到爆破针的临界载荷Fcr时，爆破针将会转为失稳状态，此时极小的轴向荷载增大都会导致爆破针的屈曲失稳。当爆破针发生失稳后，它就丧失了承载能力，阀瓣所受的反力会随着爆破针屈曲失效后急剧减小，如图2所示。由图2可知，极小的轴向荷载增加也会导致爆破针产生极大的弯曲变形。因此很适合作为触发泄压装置的结构。

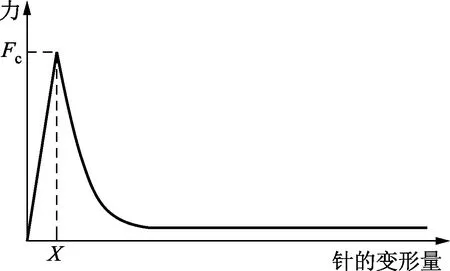
Fc为爆破针因变形产生的反力；X为爆破针的变形量图2 爆破针的支撑力与变形量的关系Fig.2 The relationship between the support force and the deformation of buckling pin

1.1 物理模型

爆破针型泄压阀属于对称结构，故选取流体计算区域取一半的流场空间建立模型，流体介质为水。模型外形尺寸与实际尺寸一致。所用爆破针的直径为3.5 mm，长度为150 mm。将阀盖从阀门结构中独立出来，建立了阀盖的疲劳损伤分析模型，以Q235碳素钢作为阀门的材料，它的屈服强度为235 MPa。阀体和阀盖的物理模型分别如图3、图4所示。

图3 爆破针型泄压阀简图Fig.3 Photograph of buckling pin valve

图4 阀盖物理模型Fig.4 Physical model of valve cover

1.2 数学模型

1.2.1 湍流模型

由于阀腔内部处于湍流状态且需要对近壁区域有较高计算精度，采用SSTk-ω(shear stress transferk-ω)模型，湍流动能k和湍流耗散率ω方程如式(1)、式(2)所示[16]。

湍流动能k：

(1)

湍流耗散率ω：

(2)

式中：ρ为流体密度；t为时间；xi、xj为位移的张量表示；ui为速度的张量表示；Gk为湍流动能；Gω为涡量方程；Γk、Γω分别表示k与ω的有效扩散项；Yk、Yω分别表示k与ω的发散项；Dω表示正交发散项；Sk、Sω为用户定义的源项。

1.2.2 动网格技术

采用动网格技术，对于任意边界移动的控制体积V对一般标量φ有守恒型方程[16]：

(3)

式(3)中：V为大小形状随时间变化的控制体积；∂V(t)是控制体积的运动边界；u为速度矢量；ug为动网格的运动速度；ρ为流体密度；A为控制体的表面积向量；Γ为耗散系数；Sφ为φ的源项。

对于阀瓣运动区域的流体计算域，采用局部网格重构的方法实现3D网格的重新划分与合并。通过用户指定网格歪斜率和尺寸阈值控制网格的局部重构。

1.2.3 阀瓣的刚体运动UDF

将阀瓣视作运动刚体，通过用户定义函数(user-defined function,UDF)模拟阀瓣在流体作用和爆破针反力作用下的运动状态。对于爆破针阀的阀瓣，其受流体力和爆破针反力的共同作用而运动，满足牛顿第二定律：

(4)

vt=vt-Δt+(F/m)Δt

(5)

式中：F为阀瓣所受合力；m为阀瓣质量；v为阀瓣运动速度；t为时间。

对于阀瓣运动区域的网格，采用扩散光顺与局部网格重构相结合的动网格技术。根据阀瓣的运动方程编写UDF程序，模拟爆破针型泄压阀动态开启的过程。通过UDF分别求解流体力与爆破针对阀瓣的反力，并以此为基础求得阀瓣所受合外力，依据牛顿第二定律计算阀瓣的加速度，从而实现对阀瓣运动状态的模拟。爆破针在阀门泄放过程中的变形量与反力的关系通过实验得到，将数据拟合为双折线函数加载到刚体运动的UDF中，即为爆破针型泄压阀的阀瓣。图5为拟合的双折线函数图像。通过编写的DEFINE_CG_MOTION宏实现阀瓣的运动状态模拟。

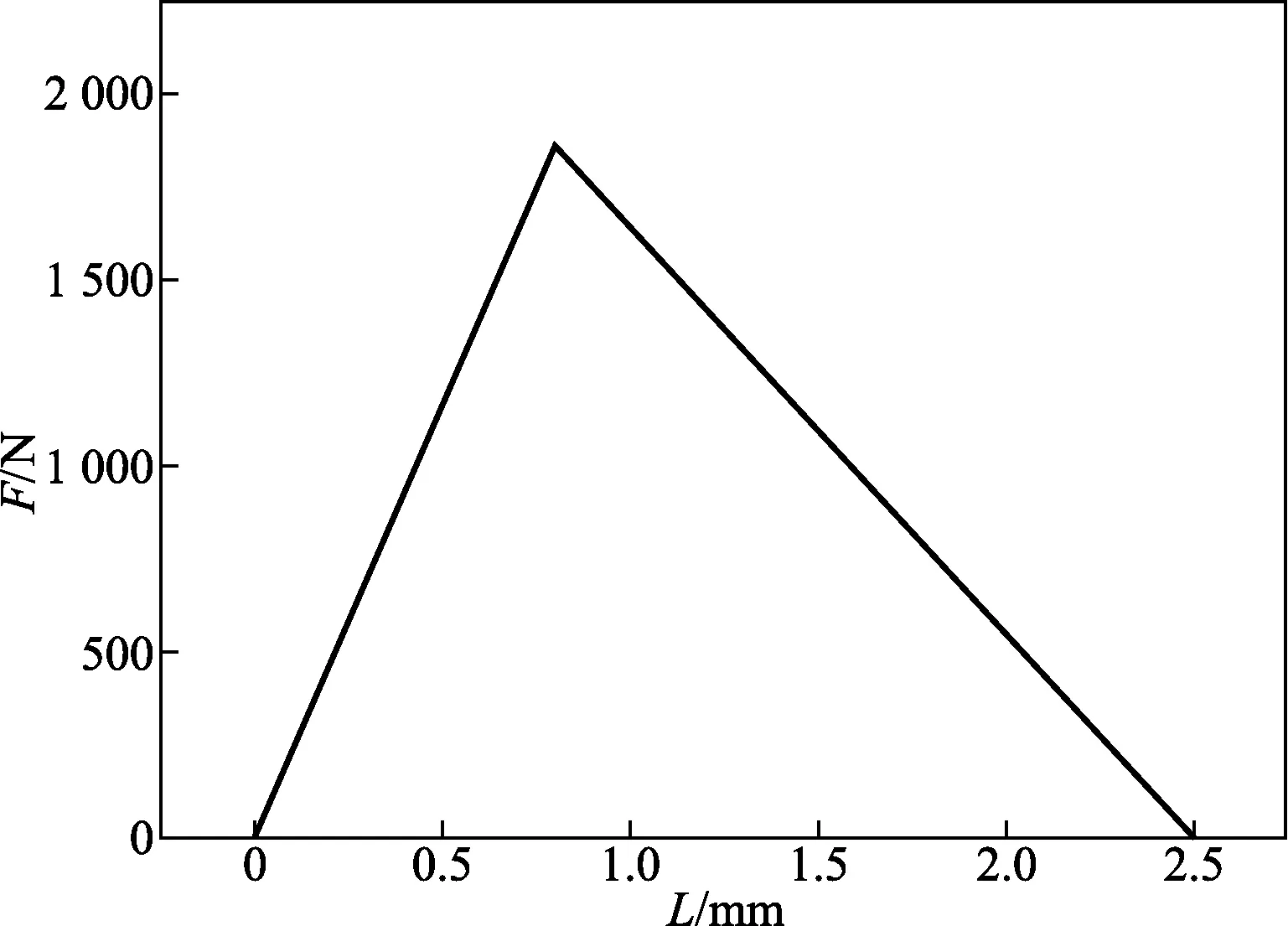
L为爆破针的变形量图5 直径3.5 mm爆破针形变与反力函数图Fig.5 Deformation and reaction function diagram of buckling pin with diameter of 3.5 mm

1.2.4 塑性理论

塑性是一种在某个给定载荷情况下材料出现永久变形的情况。大多数工程材料在所受的应力低于其比例极限时，它的应力应变曲线呈线性变化关系，当材料所受的应力低于屈服点时，表现为弹性行为，即当材料所受应力消失时，材料产生的应变也会消失。而当材料所受应力超过比例极限时，材料产生的塑性应变在应力消失后依然存在。

屈服准则是一个标量的，它可以用来表示与单轴测试的屈服应力相比较的应力状态。依据屈服准则，程序就能通过确定材料结构的应力状态来判断其是否出现塑性应变。图6为Von Mises屈服准则，是一个通用的屈服准则。

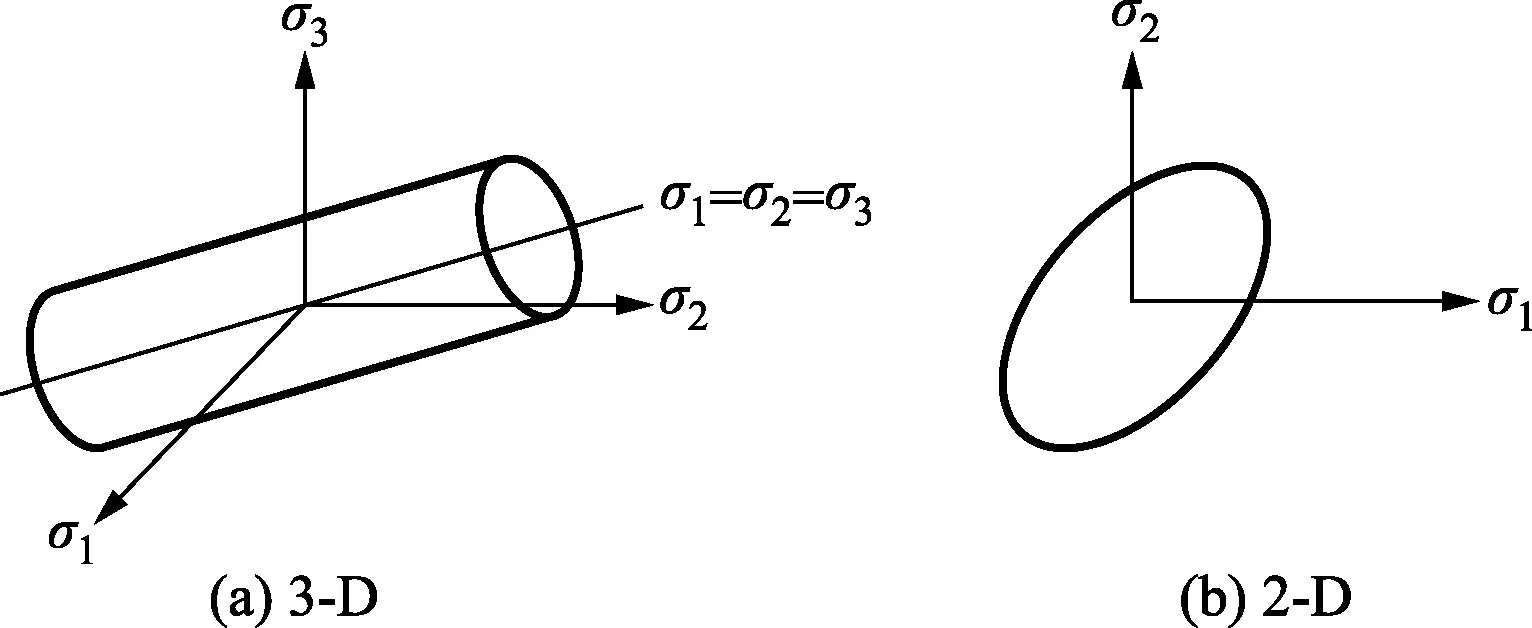
图6 主应力空间中的Mises屈服准则Fig.6 Mises yield criterion in principal stress space

在三维主应力空间中，屈服面是一个以σ1=σ2=σ3为轴的圆柱面，而在二维主应力平面中，屈服面是一个椭圆，当材料的应力状态处于屈服面内时，其表现为弹性行为，而当应力状态处于屈服面外时，则表示材料屈服，会表现塑性行为，出现不可逆的变形。流动准则描述了当材料表现塑性行为时，塑性应变的方向。强化准则描述了初始屈服准则随着塑性应变的增加是如何发展的。主要使用等向强化和随动强化这两种强化准则，如图7所示。

图7 两种强化准则的屈服面变化Fig.7 Yield surface changes of two reinforcement criteria

等向强化的屈服面对于Mises屈服准则来说，会在所有方向上均匀扩张，材料在受压方向的屈服应力等于受拉过程中的最大应力。而随动强化准则是假定屈服面的大小保持不变且仅在屈服的方向上移动，当一个方向的屈服应力升高时，其反方向的屈服应力则应该降低。采用双线性等向强化的弹塑性本构模型对阀盖在冲击作用下的应力应变和疲劳寿命进行计算分析。

1.3 网格划分与求解设置

为了提高计算效率并保障计算结果的准确性，将流体计算区域分为三个独立的部分分别划分网格，分别为入流流道、动网格区域和出流流道。动网格区域采用四面体网格进行划分，其余两个计算域采用六面体网格划分。将网格更新限定在动网格区域内以提高计算效率。三个流体计算域之间通过滑移界面即interface连接。由于在软件的流体计算中无法计算两个完全重叠的边界，并且为了能够保证阀瓣在初始状态时不会出现泄漏的情况，在阀瓣闭合时设定了一个较小的初始开高，为0.5 mm。阀盖模型按照实际尺寸建立，模型以六面体结构性网格进行划分。网格划分如图8所示。为了得到阀瓣对阀盖局部的冲击力，以流体计算结果为基础，通过动量定理[式(6)]可计算得到阀盖在受到阀瓣碰撞瞬间所受的冲击力。

Ft=mv

(6)

式(6)中：F为阀盖所受的冲击力；t为阀瓣与阀盖的冲击时间；m为阀瓣质量；v为发生碰撞时阀瓣的速度。

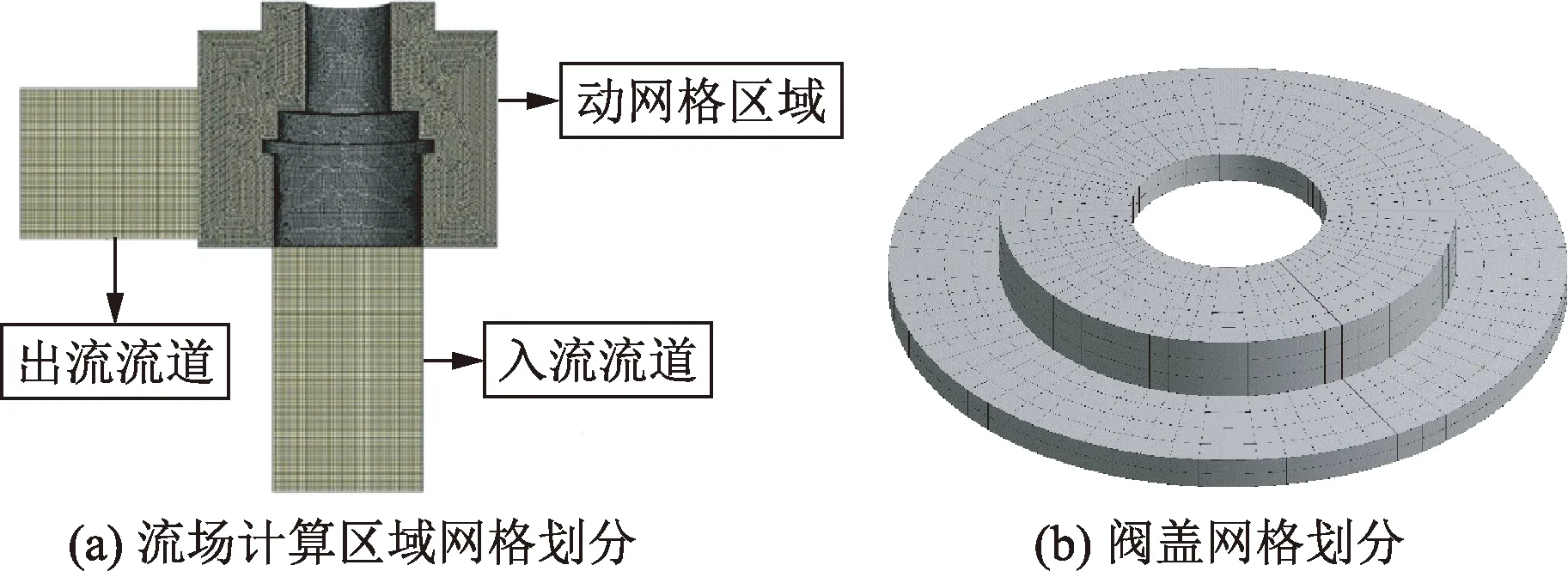
图8 流体计算区域和阀盖的网格划分Fig.8 Grid division of fluid calculation area and valve cover

流体计算区域的入口处和出口处为压力边界条件，通过改变入口边界的入口压力计算不同工况下的阀门性能参数，并将出口压力边界的初始静压设置为0。流场外侧壁面为固壁面。由于选取了 1/2 的流体计算域进行计算，因此在对称面上使用对称边界条件。在软件的动网格设置中，将阀瓣视作运动刚体并通过加载编写的刚体运动UDF来实现阀瓣的运动。将对称面和阀瓣上方的运动壁面设置为变形边界，即随着阀瓣的运动，会通过软件的网格重构功能不断更新该边界面上的网格。当完成了模型的网格划分，湍流模型选择以及边界条件设置后即可进行求解设置并进行求解。由于阀腔内部属于高湍流的状态，且动网格计算精度要求较高，使用PISO算法进行压力-速度耦合以避免SIMPLE算法中压力场偏离过大的问题[17]。阀盖的疲劳分析模型中边界条件的设置较简单，将阀盖与阀腔连接处设置为固壁面，通过改变施加在阀盖上的冲击力计算阀盖在不同工况下的应力应变分布与疲劳寿命。

2 计算结果与分析

2.1 流场参数分析

2.1.1 漩涡分布以及速度场分析

以入口压力为1.6 MPa的超压泄放情况为例，为了探究爆破针阀在超压泄放过程中阀腔结构及阀瓣运动对流场的影响，平均选取了阀瓣开启过程中的四个不同开启高度的时刻对流场参数进行分析，这四个不同开度分别对应0.6、1.5、2.5、5 ms这四个不同的时刻。

在阀瓣开启过程中，漩涡的烈度及速度场分布分别如图9、图10所示。

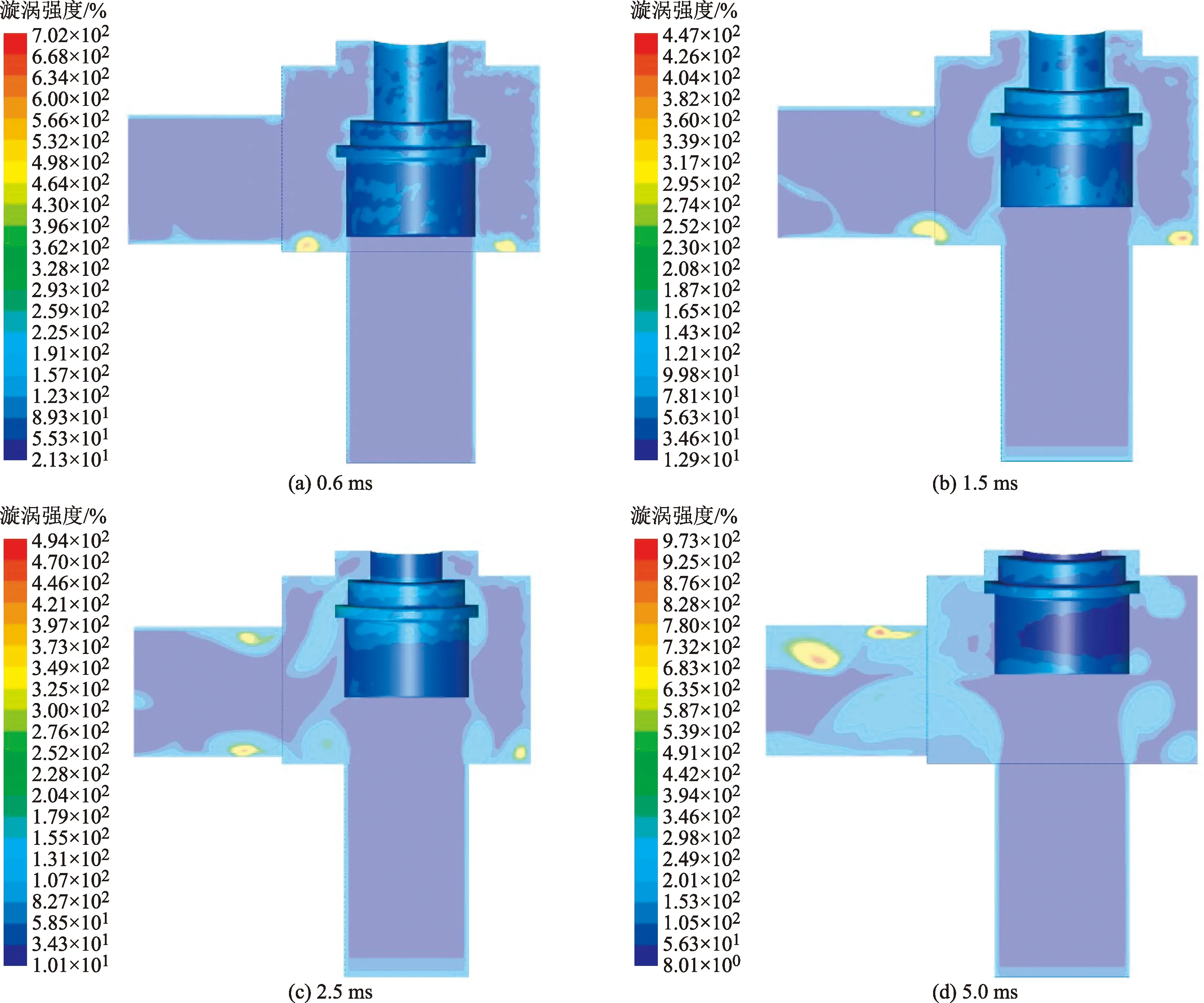
图9 进口压力1.6 MPa下不同时刻的漩涡强度Fig.9 Vortex intensity at different time under 1.6 MPa inlet pressure

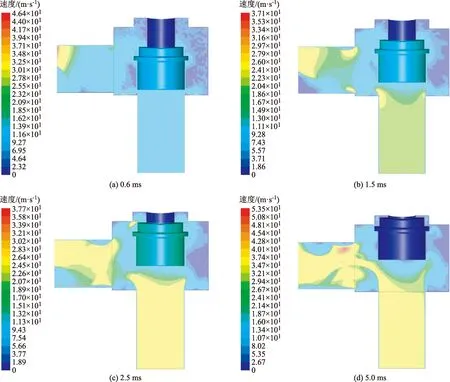
图10 进口压力1.6 MPa下不同时刻速度场云图Fig.10 Velocity field at different time under 1.6 MPa inlet pressure

当阀瓣开启瞬间，随着介质快速流入阀腔，喉部两侧开始出现漩涡并向阀门内部泄放；随着阀门开启，阀瓣向上移动，阀门内部结构凸角也会使流体产生漩涡，并随着阀瓣开启高度增加，流速加快，漩涡的强度也会逐渐增大。并且集中在出口流道上下壁面、入口流道喉部上端和阀瓣凸角处。由于阀腔内部结构的快速变化对流场的扰动极为明显，因此在整个开启过程中，流场是逐渐向高湍流发展的，且在阀瓣全启的瞬间处于极度强烈的状态，流场参数变化幅度很大；当阀瓣停止运动后，阀门结构对流场参数的影响减弱，流场参数逐渐变得平稳，达到稳定泄放。漩涡的产生主要原因是阀腔本身的内部结构以及阀瓣的运动，内部结构的突变导致了流场参数的强烈变化，说明阀门自身结构会影响流场参数，在泄放初期阶段，入口处介质流速接近0 m/s，随着阀瓣的开高增大，介质会以高速射流的状态向阀门内部运动，由于介质为水，且密封段在阀瓣开启前是无介质充填的状态，在阀门密封段出现了散射状的速度分布图像。随着阀瓣向上运动，可以明显看到阀瓣以及阀腔内部结构凸角周围介质流速较低，介质速度的突变都发生在结构突变处，这是由于结构凸角处会产生湍流漩涡，极大影响介质的流动状态使得阀腔内部速度场变化很剧烈。在泄放过程中，随着阀瓣开高不断增大，入流流速不断增大，并在出口流道上下壁面产生高速回流，对流场产生强烈扰动。对比2.5 ms时刻与 5 ms 时刻速度场可以看到，入流流速在阀瓣开启瞬间增大后几乎保持不变，当阀瓣停止运动时入流速度有明显的增大，说明介质流速主要受阀瓣运动特性的影响，可以通过结构优化的方式以降低流场的扰动来提高流体介质的泄放效率和提升阀门安全性。

2.1.2 阀门的泄放量及运动学参数分析

当然，何翔父亲的心态可能不够“端正”。据称，何翔平时爱好表演，这不是什么问题，有着各种爱好的孩子很多，家长在能力范围内培养孩子的爱好、满足孩子的兴趣，也算正常。可是，有必要通过花钱买参演的方式来培养和满足孩子的表演兴趣吗？从影楼里听来的消息，花钱买来的角色，即便“签约那天，现场负责人说只有五个名额的‘一号角色’”，稍有点儿常识的人也会知道，这种做法很不靠谱，家长未免显得太着急了。

为了探究阀门在接近临界泄放压力和超压泄放状态下的性能参数，分别对入口压力为0.1、0.2、1.2、1.6、3 MPa这5种入口边界条件下的阀门泄放进行了数值模拟，结果分析如下。

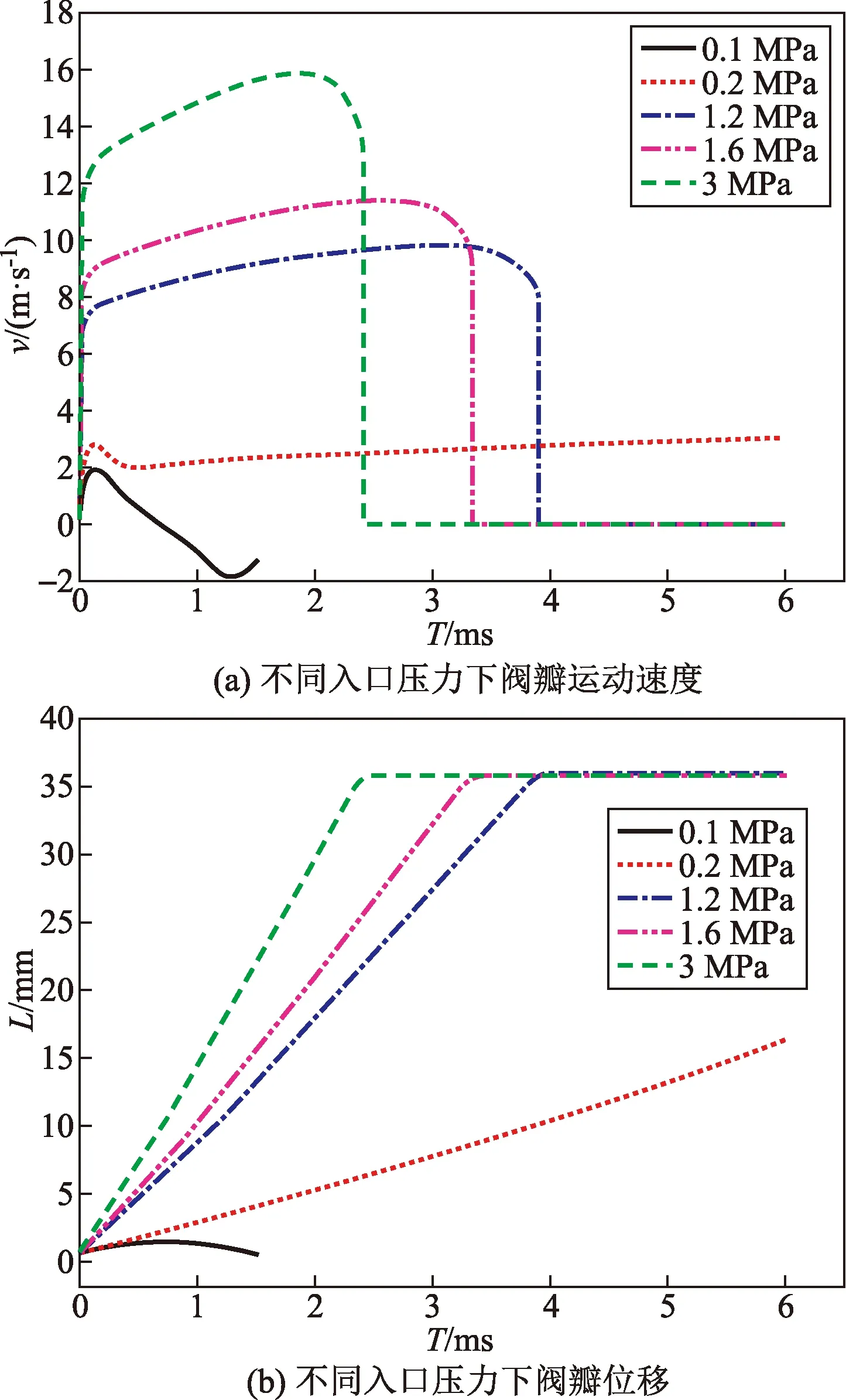
T为阀门开启过程中的时刻图11 阀瓣运动情况Fig.11 Valve clack movement

图12 进口压力1.6 MPa下入流边界处压力变化Fig.12 Pressure variation at inflow boundary under inlet pressure of 1.6 MPa

图11、图12分别为阀瓣在不同入口压力下的位移及运动速度曲线和1.6 MPa入口边界的压力变化图。阀瓣的动态特性主要受流场影响，且运动速度与进口压力正相关；随着入口压力不断增大，阀瓣运动速度增大，阀门全启的时间缩短。在0.1 MPa时，阀瓣的运动速度在0 m/s上下震荡，且位移值在达到1.36 mm后逐渐回到0，结合泄放量的变化情况可以看到阀门的泄放量出现负值，说明阀门可以视作未泄放，这也符合爆破针型泄压阀的特性，即在未达到泄放压力时可以保证密闭性。区别于普通弹簧式安全阀的阀瓣在临界压力下会出现起跳[18]从而影响密封性能的情况。在超压泄放状态下，阀瓣的运动速度在开启瞬间会突然增大，随后以一个较平稳的加速度逐渐增加，最后存在一个较短的减速阶段并突然降到0。首先，由于爆破针在在形变超过0.8 mm后即会失效变形，而此时处于超压泄放下，通过对比图12中的入口压力变化，可以看到，喉部压力会逐渐积聚，当爆破针失效后，喉部积聚的高压会使得阀瓣的加速度非常大，在短时间内速度达到一个峰值；而后随着阀瓣开高的增大，积聚的压力逐渐释放，动压的变化变得平稳，阀瓣的加速度逐渐减小，增速也逐渐放缓；直到阀瓣接近全启时，由于此时阀腔顶部流体介质受到压缩，导致静压的积聚，当阀瓣运动时动压占主导，影响阀瓣的运动特性，随着阀瓣接近阀盖，积聚的静压使得阀瓣开始减速，直到受到阀盖的限制，突然降为0。图13、图14分别为不同入口压力下入口和出口边界的泄放量及阀瓣停止瞬间前后时刻的压力场分布。

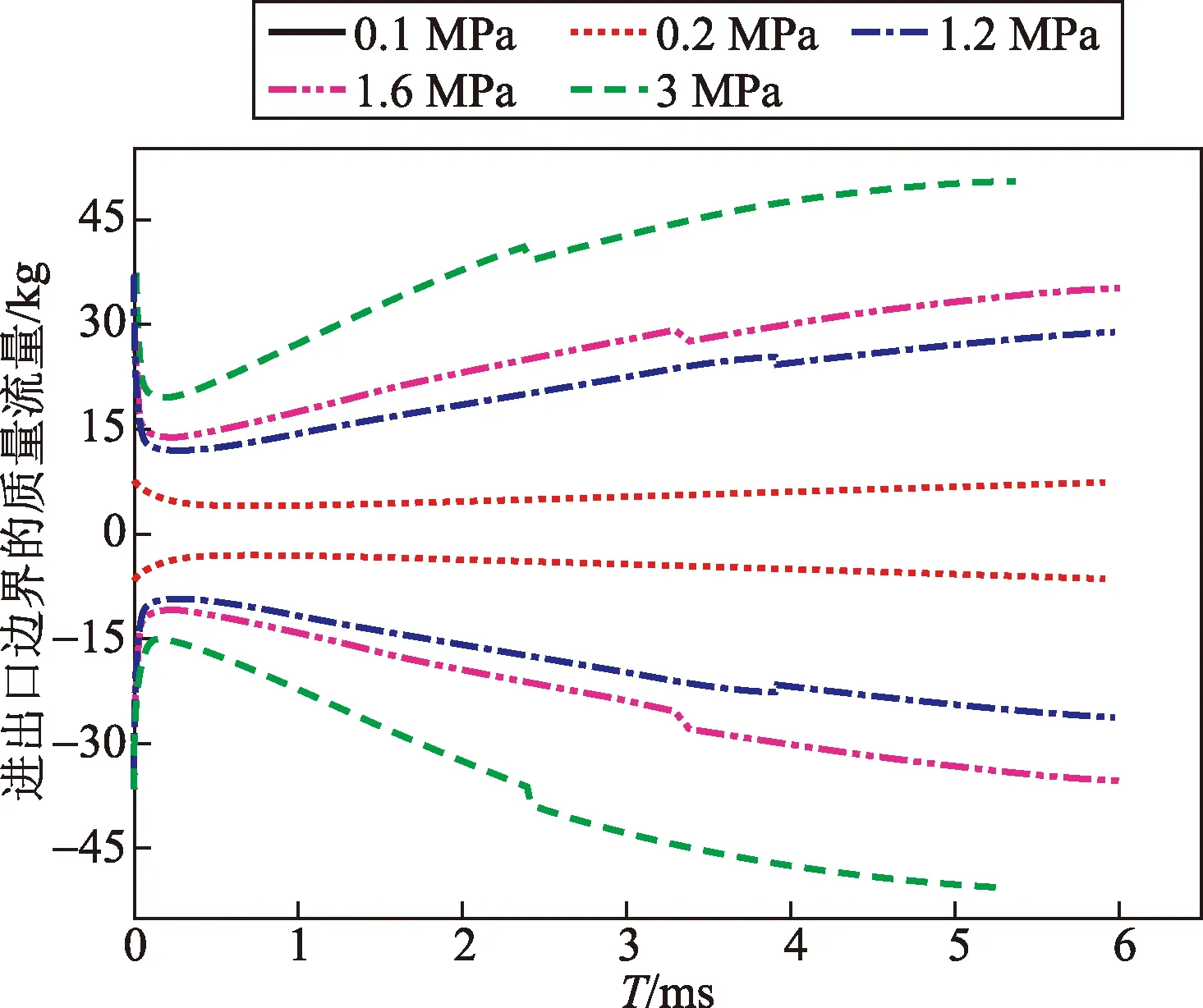
图13 不同进口压力下出入口边界质量流量Fig.13 Mass flow at entry-exit boundary under different inlet pressure

图14 阀瓣停止运动前后时刻压力场分布Fig.14 Pressure field distribution before and after valve clack stop

由于流体在阀腔出口处的法向流速与出口截面处法向量相反，所以出口处监测值为负值。0.1 MPa下，阀门入口处介质出现了回流的情况，说明此时阀瓣的开度可以视作阀门未泄放，也说明所采用的初始开高是可取的。对比阀瓣的运动速度图像可以看到，阀门的泄放量在阀瓣受到阀盖限制停止时会出现一个突变。泄放量变化曲线显示，在阀瓣停止运动前，泄放量呈现匀速增长的态势，而随着阀瓣由于阀盖的限位停止运动后，泄放量的增速会放缓并逐渐区域稳定。这说明阀腔内部结构会对阀门的泄放造成影响，且阀瓣运动状态的突变会影响阀门的泄放稳定性。阀门泄放量的突变发生在阀瓣停止运动的时刻，图14为阀瓣停止瞬间前后时刻的压力场分布对比，当阀瓣停止运动后，阀腔内部结构不再变化，流场机理主要受静压分布的影响，在阀瓣停止运动后的时刻，入流流道处的总压增大，而随着阀瓣停止运动，原本阀瓣上方积聚的静压转移至阀腔导致阀腔内部压力陡增，使得泄放量在阀瓣停止运动时出现突变。

2.2 阀盖疲劳分析

阀瓣的质量为0.783 kg，通过对流场的瞬态数值模拟得到在1.2、1.6、3 MPa这三种超压泄放状态下阀瓣与阀盖撞击前的速度分别为8.18、9.69、13.39 m/s，假设阀瓣与阀盖的冲击时间为 0.5 ms，根据式(6)，可以得到在这三种超压泄放状态下，阀盖所受冲击力分别为12 810、15 175、 20 969 N。由于爆破针型泄压阀在每次泄放完成后都需要设置新的爆破针，并重复使用的，因此单次受冲击力情况下的应力应变分析不足以满足真实的工程应用需要。所以分别将阀盖在三种超压泄放的情况下所受冲击力循环10 000次施加在阀盖上进行结构的疲劳分析。分别对三种冲击力各循环10 000次下的结构安全系数、阀盖在三种冲击力下循环下的寿命以及阀盖的疲劳敏感性进行分析。

图15 阀盖的塑性应变云图Fig.15 Plastic strain of valve cover

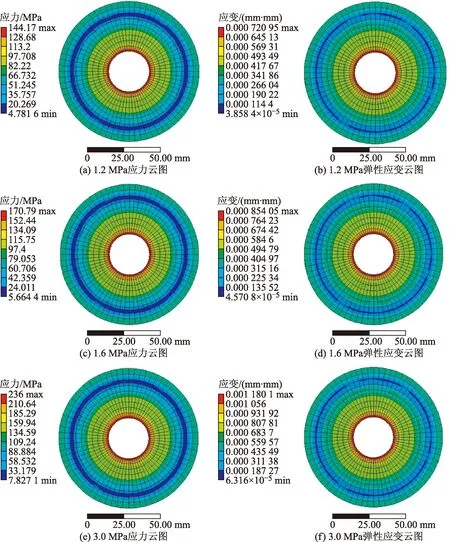
图16 阀盖的应力及弹性应变云图Fig.16 Stress and elastic strain of valve cover

图15、图16分别为阀盖在三种进口压力下受单次冲击的应力应变云图。由图15、图16可知，在三种冲击力的单次作用下，阀盖没有出现塑性应变区，说明阀盖在这三种受力情况下都没有出现塑性应变，即在单次冲击下阀门的结构是安全可靠的，且阀盖的应力应变分布是一致的，越接近阀盖中心处，应力应变越大，并且随着与阀盖中心距离的增大，应力应变都逐渐减小。而在阀盖与阀体顶部结构突变处，应力应变都出现了突然减小。因为在阀盖与阀体顶部连接处的结构在冲击力作用下基本呈轴向受拉的受力方式，而其他部分的结构受剪应力较大，轴向受拉的部分结构相对比较安全。说明在阀瓣的冲击下，阀盖整体都承受了较大的应力，而在阀盖与阀体顶部的结构突变处所受应力较小，相对较安全。而阀盖的中心处最容易出现塑性应变和损伤破坏。图17为阀盖在三种不同冲击力各循环10 000次下的结构安全系数及三种冲击力循环下的寿命。

图17 阀盖安全系数及循环寿命Fig.17 Safety factor and cycle life of valve cover

由图17可知，在三种冲击力分别循环10 000次的情况下，阀盖的最低安全系数分别为1.99、1.68、1.22，说明在假设循环10 000次的情况下，阀门可以满足工程上的安全系数要求，并且通过循环寿命的分析可以看到，在1.2 MPa的泄放下压力，阀盖在循环达到20×104次左右后达到疲劳损伤，在1.6 MPa下循环次数为12×104次左右，而在3 MPa下仅为2.6×104次左右，随着泄放压力的增大，阀盖的循环寿命会急剧减少，并且损伤部位会从阀盖的中心点位置逐渐扩散到整个阀盖上。通过分析阀盖的安全系数及循环寿命可以得到，阀盖在超压泄放的情况下可以保证结构的安全性，但随着泄放压力的增大，阀盖的循环寿命不是呈线性的减少，而是会出现循环寿命的突然减少。

同样在三种泄放压力下，对阀盖在冲击力作用下的疲劳敏感性进行分析，设置阀盖所受的最小荷载变化幅度为20%，最大荷载变化幅度为150%。图18为三种不同情况下阀盖的疲劳敏感性变化。

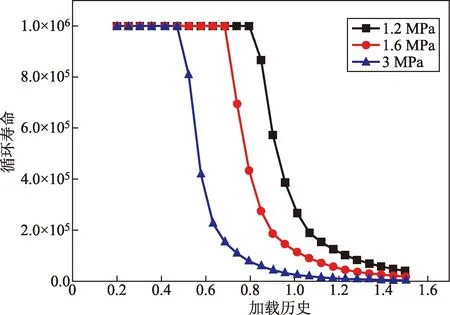
图18 三种泄放压力下阀盖的疲劳敏感性Fig.18 Fatigue sensitivity of valve cover under three relief pressures

由图18可知，3种冲击力情况下，当荷载幅值分别达到某一值后，阀盖的循环寿命会出现骤减，泄放压力1.2、1.6、3 MPa对应的循环寿命突变时的荷载幅值分别是10 119、10 319、9 855 N，这三个值非常接近，且都在10 000 N左右。说明阀盖的循环寿命在承受10 000 N左右的冲击力情况下会出现骤减。也就是说，当阀盖承受的冲击力小于10 000 N以下时可以不用考虑阀盖的疲劳损伤，此情况下阀门的结构是安全可靠的。当阀盖承受的冲击力大于10 000 N时，需要考虑阀盖在不同泄放压力下的循环寿命，对阀盖进行疲劳损伤分析以对工程应用做出可靠的疲劳分析和损伤预报。