基于非平稳信号组合分析的故障诊断方法

陈哲，胡玉其，田世庆，陆慧敏，徐立中

（1.河海大学计算机与信息学院，江苏 南京 211100；2.日本九州工业大学机械智能工学研究系，北九州 804-8550）

1 引言

振动、温度、压力等非平稳信号产生于能量转化过程中，普遍存在于工业生产各环节，对其分析和处理是工业过程控制、状态估计、故障诊断等研究的课题之一[1]。对于此类信号，传统分析方法多提取具有明确物理含义（如频谱、时频信息）的信号特征来表征设备状态信息，常用方法包括时−频域统计特征分析[2]、快速傅里叶变换[3]、小波变换[4]、时频图分析[5]、经验模式分解[6]以及信号统计学特征[7]等。该类方法有利于构建运行状态与原始信号间的因果耦合关系模型，受到了广大研究者的推崇。然而，基于此类模型驱动的技术策略的不足之处在于特征表征的冗余度大、噪声强、不同状态特征间的类间差异性不足。为了解决这一问题，多种降维技术被应用于后续处理环节，常采用的方法包括主成分分析法[8]、独立分量分析法[9]、流形学习[10]等，在一定程度上实现了冗余压缩，但是仍难以提高特征的表征能力，影响故障诊断、状态估计等应用的分类准确率。近年来，深度学习相关方法被应用于非平稳信号分析。不同于传统基于模型的信号分析方法，深度学习通过大数据驱动的学习及多层样本映射，能够提取高度抽象化且具有极强表征能力的深度表达特征，具有优越的状态辨识能力，深度置信网络[11]、稀疏自编码器[12]、去噪自编码器[13]、卷积神经网络[14-16]等模型被广泛应用于非平稳信号分析。然而，大量的研究证明，该类学习方法的不足之处在于，所提取的深度表达特征缺乏明确的物理含义，难以有效解析信号属性，特征性能常出现较大波动，稳定性和推广性均难以适应。

现有频谱、时频分析或深度学习等多类非平稳信号分析方法各具特色，在信号特征的解析性、稳定性和准确性上难以权衡。考虑到非平稳信号频谱、时频和深度表达特征各自的优缺点和互补性，本文提出了一种非平稳信号组合分析方法，能够并行提取信号的多类特征并加权融合。在以振动信号为例应用于故障诊断的实验研究表明，所提信号组合分析方法具有较好的特征表征能力，在不显著增加计算复杂度的前提下有效提高了故障诊断的准确性。同时，本文研究工作是对基于特征融合的故障诊断方法的一项探索。本文的主要创新和贡献如下。

1) 特征提取。提出了一种双流网络架构，组合分析非平稳信号的频谱、时频及深度表达特征，以实现对信号的完整描述。

2) 特征融合。提出了基于压缩−拼接−激励（SCE，squeeze-connect-excitation）的双流特征加权融合方法，以实现非平稳信号特征的统一表征。

3) 特征辨识。在故障诊断实验中，所提组合分析方法能够有效提高诊断准确性，有望满足工业条件下的应用需求。

2 相关研究

故障诊断领域的非平稳信号分析及特征提取方法主要分为基于信号处理模型和基于深度学习的技术策略。

信号处理模型能够清晰表征信号的物理属性，如时变、频谱和频谱时变属性等。例如，文献[3]利用全局谱分析方法对非平稳振动信号进行分析，综合采用包络检测方法与快速傅里叶变换方法进行信号预处理。文献[4]使用小波变换和包络谱分析，从非平稳信号中提取特征参量，并输入故障诊断系统中进行故障分类。文献[6]利用能量算子解调理论和经验模态分解方法，对轴承非平稳振动信号的特征进行提取。文献[7]提出了基于小波变换高阶统计量的非平稳信号分析及滚动轴承故障诊断方法，该方法采用小波变换的四阶统计量有效捕捉振动信号中的非平稳或奇异分量，以表征信号的奇异性。

深度学习方法能够提取高度抽象化且具有极强表征能力的深度表达特征，在信号特征辨识和分类中展现了良好的性能。例如，文献[11]借鉴深度置信网络在处理高维、非线性数据方面的性能优势，提出一种基于深度置信网络的信号分析及故障诊断方法，利用原始时域信号训练深度置信网络并完成智能诊断。文献[12]提出了一种基于深度迁移学习的故障诊断方法，采用三层稀疏自编码器对原始信号直接提取特征，应用最大差分项最小化训练数据和测试数据特征之间的差异惩罚。文献[14]提出了基于一维卷积神经网络的信号分析方法，将电机故障检测的特征提取和分类合并到单一的学习体中，有效提高了诊断效率。文献[16]直接将原始振动信号输入一维卷积神经网络进行训练，并通过自适应批量正则化计算提高变负载能力。

此外，部分研究还探索了基于级联模型的信号分析方法。例如，文献[17]将傅里叶变换与卷积神经网络模型结合，用于提取非平稳信号特征。文献[18]将多信号特征输入卷积神经网络模型，提取深度表达特征，由于多级映射过程，此类级联信号分析方法所获信号特征难以准确解析原始信号属性，且常出现“过拟合”的问题。

3 非平稳信号组合分析

如图 1 所示，本文所提出的非平稳信号组合分析方法采用双流网络框架，主要包括2 个分支流：上分支信号处理流主要完成傅里叶变换和小波包分解，用于频域和时频域的信号分析；下分支深度学习流由级联卷积神经网络（CB-CNN，cascade block convolutional neural network）组成，通过大数据驱动的多级映射过程提取深度表达特征。在多流特征融合中，本文提出基于SCE 模块的特征加权融合方法。此外，为了适应故障诊断应用的需要，后端分类器采用2 个全连接层和一个Softmax 计算层相组合的精简设计方案。

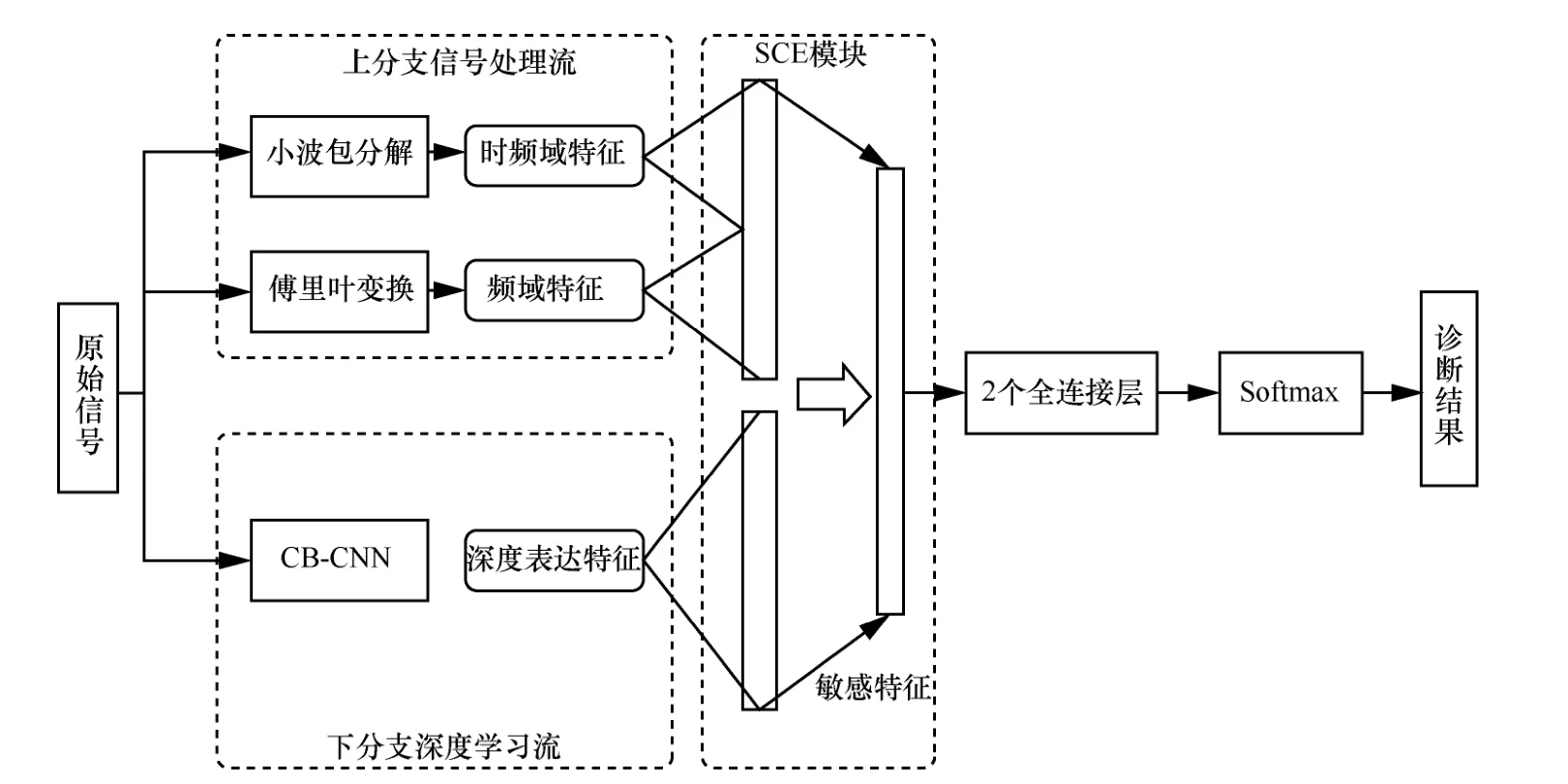
图1 非平稳信号组合分析方法框架

信息间互补性是信号组合分析可行性和合理性的基础，本文所提出的双流信号组合分析方法所提取的特征间具有明确的互补关系。在上分支，基于傅里叶变换的频谱特征能够体现信号频谱包络的全局变化特性，而小波包分解后所提取的时频特征能够体现频谱随时间变化的局部特征，二者间的融合能够从全局和局部细节上综合反映信号的频域特性。在下分支，CB-CNN 能够通过多层映射挖掘原始信号抽象化的深度表达特征，同频域和时频域特征具有明确的互补性。此外，本文的双流结构也可解释为一种联合模型驱动和数据驱动策略的并行组合分析方法，不同于以往级联式多级处理策略，本文方法能够更好地保存2 类特征本质特性并实现2 种模型的优势互补。

4 基于双流框架的特征提取

4.1 上分支信号处理流

4.1.1 小波包分解

本文采用小波包分解提取非平稳信号中的时频域特征[19]，同时对低、高频成分进行分解，以反映原始振动信号随时间变化的局部频谱特性，小波包分解过程如图2 所示。图2 中的A 和D 分别表示低频系数和高频系数，字母后的数字表示分解的层数。在此，本文选择三层小波包分解架构，共得到8 个子频带，用表示为每个子频带的重构信号，每个子频带的能量可表示为

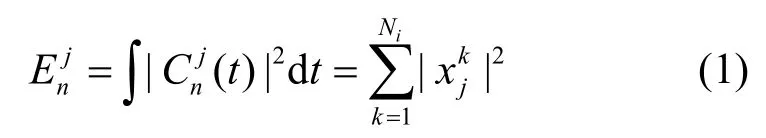
其中，n=3，j=0,1,…,7，Ni为重构信号的长度，为第j个重构信号的幅值。信号的能量均方根值可表示为

信号的能量谱特征可表示为

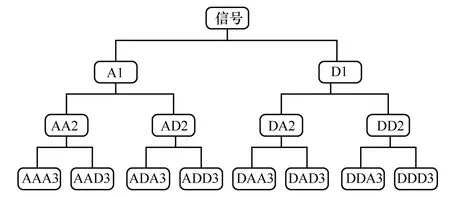
图2 小波包分解过程

4.1.2 傅里叶变换

本文采用傅里叶变换提取信号中的频谱特征。不同于时频域特征，频谱特征能够表征非平稳信号的全局频谱变化特性。对于离散的振动信号x(n)，其离散傅里叶变换可表示为

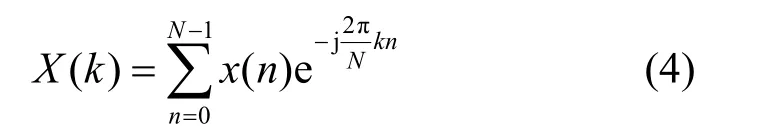
其中，k=0,1,…,N−1，N为离散序列的长度。

4.2 下分支深度学习流

本文所提双流组合分析框架的下分支由CB-CNN 构成，用于提取高度抽象化的深度表达特征。区别于上分支所提取的频谱和时频域特征，该类特征无明确的物理含义且难以解析。但得益于大数据驱动的学习过程，深度表达特征表征同设备状态间常具有强耦合相关性，有助于提高分析准确性。

下分支CB-CNN 整体架构如图3 所示。在第一层卷积计算中采用了64×1 的大尺度卷积核，通过增大感受野以更好地保存原始非平稳信号的空间及时间相关性。通过第一层卷积后经过正则化、激活层及最大池化层处理，输入后续两级级联块。

图3 CB-CNN 整体架构

级联块的详细结构如图4 所示。

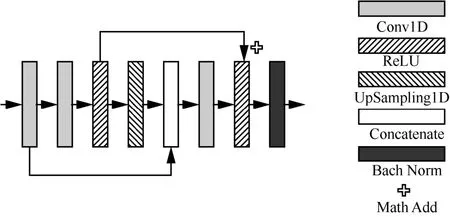
图4 级联块的详细结构

考虑到非平稳信号具有强时间相关性，会随着级联深度的增加而逐渐降低，不利于信号属性的准确表征。针对这一问题，本文设计了2 条桥接支路以保存浅层特征中的时间相关性。该级联模块由八层操作组成，包括三层卷积、两层ReLU、一层批量归一化、一层上采样和一层Concatenate 计算。其中，第一条桥接支路通过Concatenate 计算将第一层卷积结果与上采样层的输出进行连接；第二条桥接支路将前2 个激活层的输出进行融合，实现浅层特征信息传递。

4.3 基于SCE 模块的特征融合加权

在特征融合中，考虑到不同特征在表征性能上的差异，本文提出了一种基于SCE 模块的特征融合加权方法，如图5 所示。

SCE 模块包含 2 个输入，分别为下分支CB-CNN 深度学习流提取的维度为L×C1的特征矩阵和上分支信号处理流提取的1×C2的一维特征向量。本文中SCE 模块的主要流程包括 Squeeze、Connect、Extraction 和 Reweight。

1) Squeeze。采用全局平均池化操作对特征矩阵X进行压缩，以通过一维特征向量m代表二维特征矩阵X，获得全局感受野。

2) Connect。经过Squeeze 计算得到双流一维特征，采用Concatenate 操作实现多特征拼接。

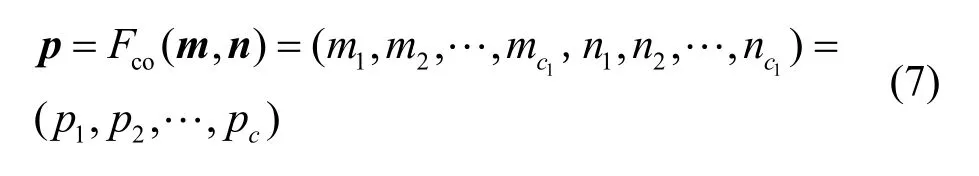
图5 SCE 模块

其中，C=C1+C2。

3) Excitation。主要通过多层次的特征降维估计特征权重q。

其中，W1和W2为学习得到的映射矩阵，δ和g为学习得到的映射函数。

4) Reweight。对特征进行加权运算，敏感特征f为

4.4 训练策略

对于所提的双流网络架构，本文设计了一种分级训练策略。考虑到上分支信号处理流采用基于模型的特征提取方法，训练过程仅需要对下分支深度学习网络参数进行优化。此时，若采用整体一次性训练的技术方案会显著增加无效的训练计算。为了解决这一问题，在第一级训练过程中对下分支的CB-CNN 进行单独训练，以生成预训练模型。第二级训练时，上下分支组合成完整网络，继续微调网络模型参数，最终实现网络整体优化。

5 故障诊断应用及实验分析

5.1 实验数据集

为了客观评价本文所提出的信号组合分析方法的性能，在故障诊断实验中进行验证和分析，采用凯斯西储大学轴承数据中心的数据集进行故障诊断实验。凯斯西储大学轴承数据中心的轴承系统平台包括3 个负载电机（1hp、2hp 和 3hp）、一个扭矩传感器和一个功率计。振动信号由加速度计以12 kHz 的采样频率采集。该数据集一共包括10 种轴承状态，分别为正常状态和9 种故障状态。故障状态包括内圈、外圈和滚动件上尺寸分别为0.007、0.014、0.021 的单点故障。对于每个负载电机，每个状态随机抽取1 000 个样本，共10 000 个样本，其中网络训练集样本为7 000 个，验证集样本为2 000个，测试集样本为1 000 个。

由于傅里叶变换和小波包分解特征具有不同的尺度，首先需要采用L2 范数归一化方法对频谱特征和时频特征进行归一化计算[20]，如式(10)所示。

5.2 参数选择和设计

本文双流网络架构主要层级的设计和参数选择如表1 所示。

表1 双流网络架构主要层级设计和参数选择

对于小波包分解，分解层数决定了时频分析的分辨率和特征的维数。本文实验首先对分解层数的选择进行优化。不同层数下小波包分解特征的分类准确率如表2 所示。从表2 中可以看到，当进行三层小波包分解时，分类准确率最高。

表2 不同层数下小波包分解特征的分类准确率

5.3 训练与微调

为了防止模型的“过拟合”和“欠学习”问题，首先对模型的收敛性进行实验验证。在本节实验中，设置训练阶段的学习率为0.01，参数微调为0.005。图6 和图7 分别为训练集和验证集的准确率曲线及损失函数曲线。可以看出，当迭代次数为10时，模型达到收敛。

图8 为测试集的混淆矩阵。其中，测试集共有1 000 个样本，共10 种状态，每个状态分别对应100个样本。从对测试集的分类结果来看，本文方法对于故障检测的结果较好，仅一例RE0.014 样本误判为RE0.021 状态。

5.4 与其他方法对比分析

5.4.1 准确率对比分析

图6 训练集和验证集准确率曲线

图7 训练集和验证集损失函数曲线

图8 测试集混淆矩阵

许多研究表明，基于深度学习的故障诊断方法在特征表征和分类正确性方面优于传统方法[21-25]。但是，深度学习网络极易陷入过拟合状态，虽然对于个别案例获得了极高的分类准确率，但仍难以取得较高的稳定性和推广性。鉴于此，本节综合选择经典的深度学习模型和浅层模型作为实验对比方法，包括SAE（stacked auto encoder）[21]、SDAE（stacked denoising auto encoder）[23]深度学习模型和Bayes[24]、支持向量机（SVM,support vector machine）[25]方法。图9 展示了10 个非冗余测试数据集上本文方法和不同经典方法的分类率，表3 为本文方法和不同经典方法的平均分类准确率对比。

图9 本文方法和不同经典方法的分类准确率

表3 本文方法和不同经典方法的平均分类准确率对比

综合分析图9 和表3 可知，本文方法明显优于传统方法，其分类准确率始终保持在99%以上。此外，SDAE 和Bayes 方法的分类准确率波动较为明显，本文方法的分类准确率稳定维持在较高水平。

为了进一步评估本文方法，选择近年来已证明较优越的深度学习方法作为对比，主要包括单分支的网络模型WDCNN[16]（deep convolutional neural network with wide first-layer kernel）和PCNN[26]（physics-based convolutional neural network），以及多分支模型MSCNN[27]（multiscale convolutional neural network ）、MC-CNN[28]（multi-scale cascade convolutional neural network）和MDI-CNN[18]（multi-dimension input convolutional neural network）。图10 展示了在10 个非冗余测试数据集上的本文方法和不同先进诊断方法的分类准确率，表4 为本文方法和不同先进诊断方法的平均测试分类率对比。

综合图9、图10、表3、表4 的结果可以看出，与其他信号分析方法相比，本文方法获得了最高的故障诊断分类率，对不同测试数据集的平均准确率达到99.85%。此外，提高网络深度是一种较为常用的提高特征表征能力的技术策略，然而，增加网络的深度常会导致过拟合问题。不同于这类技术策略，本文所提信号组合分析方法通过特征融合实现多流特征信息的互补及加权融合。与盲目地增加网络深度相比，该策略在准确性和稳定性上具有更好的表现。此外，本文方法在故障诊断中的平均测试时间为4.102 ms，实现了较高的计算效率。

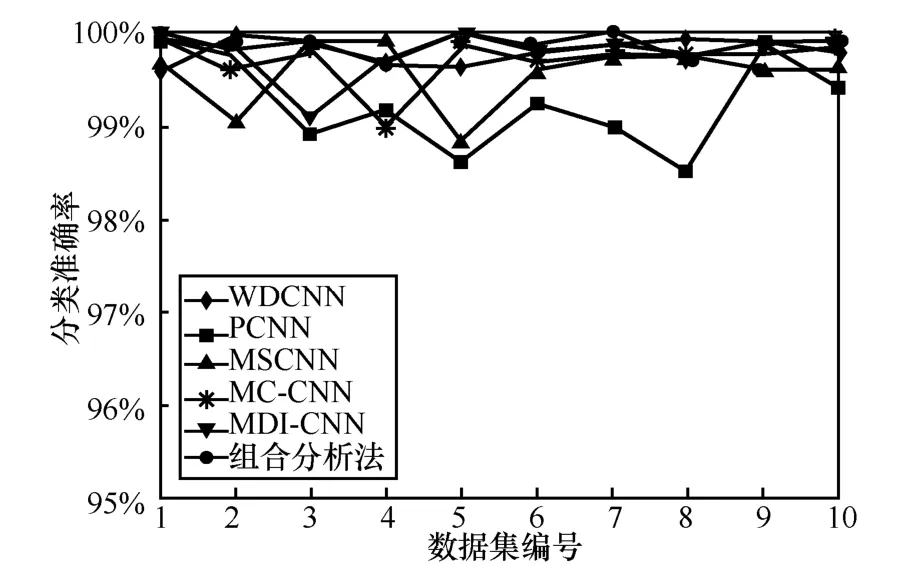
图10 本文方法和不同先进诊断方法的平均分类准确率对比

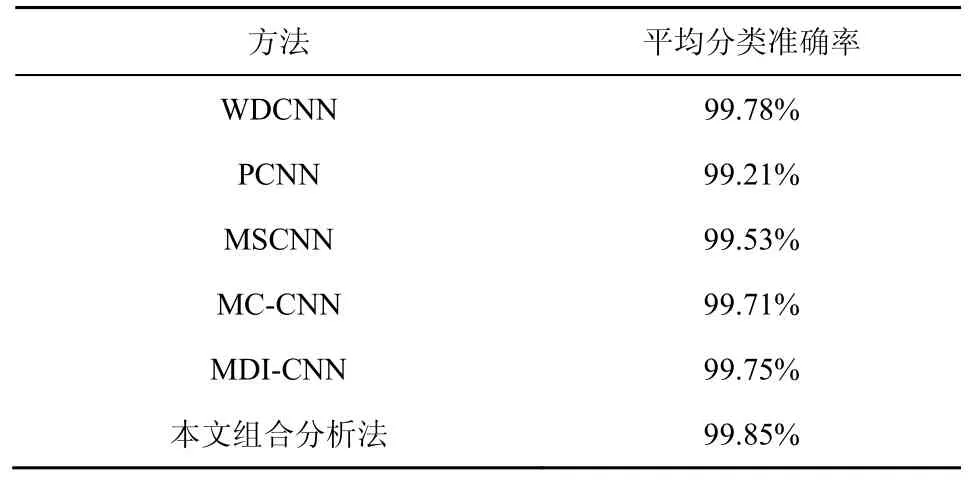
表4 本文方法和不同先进诊断方法的平均分类准确率对比

5.4.2 变噪声条件下的对比分析

为了验证本文信号组合分析方法的在不同噪声条件下适应性，本节验证其在信噪比（SNR,signal noise ratio）为−4～10 dB 条件下的分类准确率。表5 为本文方法与不同先进诊断方法抗噪性对比。可以看出，本文方法在不同信噪比条件下都获得了较高的分类准确率，仅在SNR=4 dB 时，分类准确率略低于MDI-CNN 模型。

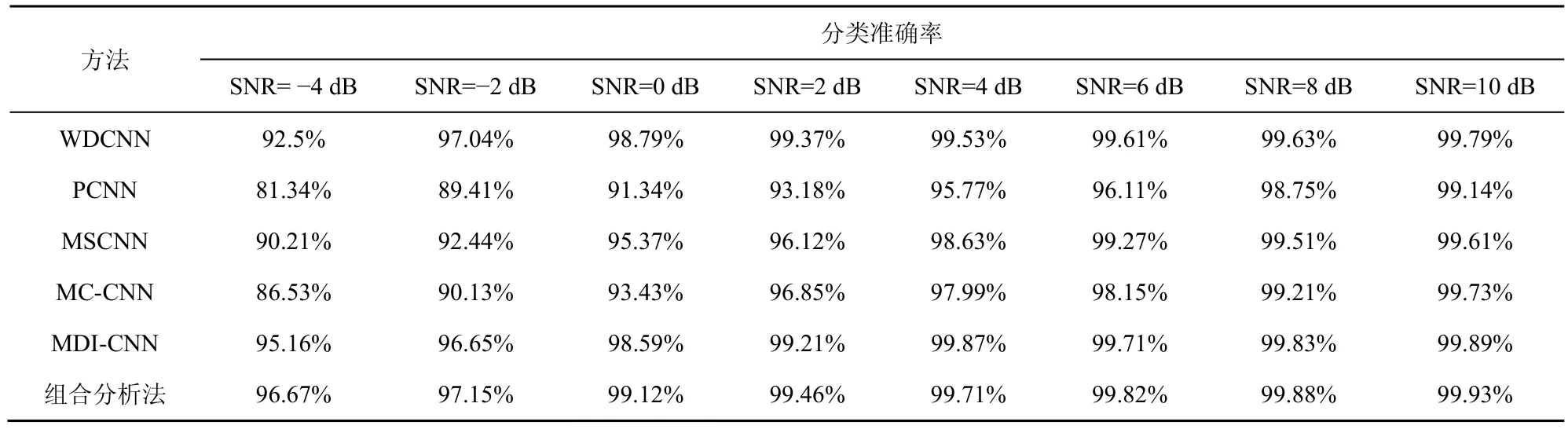
表5 本文方法与不同先进诊断方法抗噪性对比

5.4.3 变负载条件下的对比分析

在工业生产过程，仪器设备常出现负载变化，传感器信号随之变化，波动周期与相位差别显著，会严重降低特征的稳定性。

跨负载条件下的故障诊断实验（使用某一负载条件下的模型诊断另一负载条件下的故障）能够有效展示不同信号分析及故障诊断方法的稳健性和推广性。鉴于此，本文分别使用负载为 1 hp、2 hp与 3 hp 下的振动信号对双流网络模型进行训练，使用其他2 种负载条件下的信号作为测试集进行测试。表6 为变负载测试模式，图11 为本文方法与不同先进诊断方法的变负载能力对比，表7 为不同方法在不同模式下的分类准确率。

表6 变负载测试模式

从图11 和表7 中可以看到，本文方法在6 种变负载模式下均获得了较高的分类准确率，仅在模式5 下，准确率低于MDI-CNN 模型，证明了本文方法具有较好的稳健性和推广性。

6 结束语

本文提出了一种非平稳信号组合分析方法，能够综合提取频谱、时频及深度表达特征并融合，以提高对非平稳信号的表征能力。应用于故障诊断实验比较可以看到，本文所提方法能够实现较为准确和稳健的故障诊断。

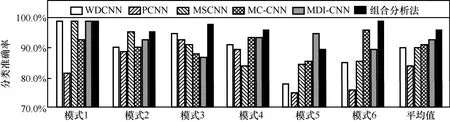
图11 本文方法与不同先进诊断方法的变负载能力对比

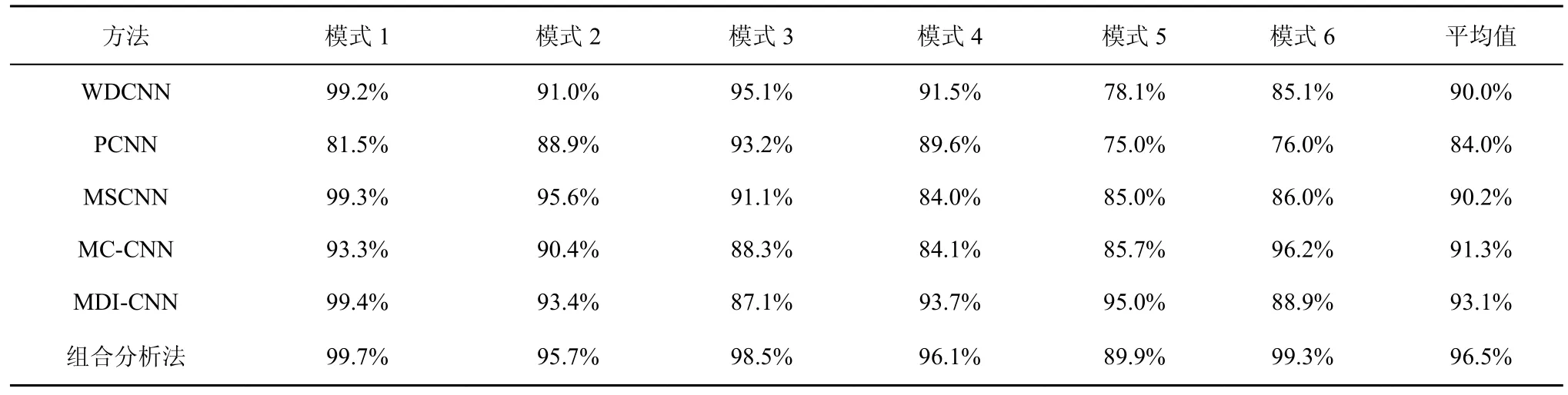
表7 不同方法在不同模式下的分类准确率

目前，多类深度学习方法在信号分析上表现出较为出色的性能，但其本质上采用完全基于数据驱动的技术策略，在实际应用中极易陷入过拟合状态，即使对于个案取得了极为优良的结果，但在方法的稳定性和推广性上仍值得商榷。此外，深度学习模型所提取的抽象化特征难以得到很好的解析，从而对未来的改进发展造成困难。与之相比，传统的信号处理方法可以提取具有物理意义的特征，这对于信号分析结果的进一步解析和研究发展尤为重要。对于故障诊断应用，多类特征间的有机融合能够有效提高诊断的准确性及稳定性，这将是未来本领域的主要发展方向之一。