基于自修正系数修匀法的网络安全态势预测

杨宏宇，张旭高

（中国民航大学计算机科学与技术学院，天津 300300）

1 引言

网络安全态势预测方法通过对网络中各种安全预警（报警）信息和关联信息的处理生成时间样本序列，通过对相关信息的进一步处理和分析获取一定时间段内的网络安全总体情况和可能变化，对及时发现网络中存在的高危态势具有积极作用。目前，灰色预测法、机器学习预测法和时间序列预测法为常见的网络安全态势预测方法[1]。

Cipriano 等[2]基于以往警报提出一种网络攻击行为预测模型。该模型将以往警报作为训练集，通过机器学习方法获得警报知识库，再根据现有警报序列预测攻击者下一步攻击行为，为实时评估网络安全态势提供参考。Xiao 等[3]提出了基于MEA-BP（mind evolution algorithm-back propagation）的网络安全态势预测方法。该方法通过对网络权重和阈值进行改进提高了安全态势的预测准确率和效率，但对以往数据的标准化不够完善。Sun[4]提出了基于复杂网络的Markov 预测模型。该模型将网络安全状况的转换关系构造成复杂网络，并利用加权马尔可夫链预测安全态势，可在一定程度上反映网络的安全状态，但面对多状态的网络，所构造出的状态转移概率矩阵规模过大。Leau 等[5]提出一种经卡尔曼滤波方程修正的网络安全态势预测模型。该模型基于层次分析法生成网络安全态势值序列，并通过灰色Verhulst-Kalman 方法动态预测网络安全态势，但局限于安全态势为单峰变化的情况。Schatz 等[6]提出一种减少不确定性的安全预测方法。该模型基于信息安全领域内具有不同程度专业知识受访者对网络安全威胁的认知语料，利用概率主题建模方法预测网络安全威胁，但受访人群的层次、经验的离散性会影响预测精度。孙卫喜等[7]提出一种网络安全态势预测方法，提高了网络安全态势预测的准确率和有效性，但所需源数据维度较多。周新卫等[8]通过灰熵关联法提取影响网络安全的主要因素，并在此基础上建立卡尔曼滤波方程，提高了安全态势预测的精度。韩晓露等[9]提出基于直觉模糊集的非线性自回归神经网络预测模型（IFS-NARX,nonlinear autoregressive neural network with exogenous inputs based on intuitionistic fuzzy set），对网络安全态势预测可靠性的提升途径做了有益的探索。

针对上述网络安全态势预测方法中存在的数据质量参差不齐以及对多峰变化的网络安全态势预测准确度降低的不足，为解决目前网络安全态势预测方法的准确性和有效性不足的问题，本文提出一种基于自修正系数修匀法的网络安全态势预测模型。

2 网络安全态势预测模型

本文提出的基于自修正系数修匀法的网络安全态势预测模型如图1 所示。其中，初始预测部分由可变域空间内的安全时间样本序列建立多重系数修匀模型以得到初始预测值；预测修正部分通过初始预测值和真实结果的偏离建立时变加权马尔可夫链，通过该模型对偏差值进行预测并修正初始预测值，最终得到网络安全态势预测结果。

模型的具体处理和分析过程设计如下。

步骤1基于熵关联度将网络警报信息转化为安全态势值非线性时间序列。

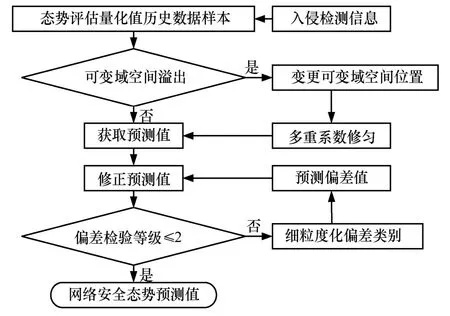
图1 网络安全态势预测模型

步骤2利用可变域空间划分网络安全态势值序列片段，每更新一个安全态势值，可变域空间即向后移动一个单位。

步骤3基于可变域空间内的安全态势序列建立多重系数修匀预测模型，并通过自适应调整静态修匀系数α以初步提高预测精度。

步骤4计算可变域空间内的安全态势预测值与实际值的偏差，将偏差划分为k个偏差区间或分区。采用时变加权马尔可夫链模型对预测值进行处理，对偏差值进行预测并对原始预测值进行二次修正。

步骤5检验偏差，若未满足阈值条件，则返回步骤4，并将偏差类别划分为k+1 个；若满足阈值条件，则按步骤1～步骤4 得到下一周期的安全态势值。

本文模型通过动态调整静态修匀系数α初步提高态势值预测精度，再通过调整偏差类别数量提高时变加权马尔可夫模型对偏差的预测精度，最终完成对安全态势预测值的自适应修正目标。

3 网络安全态势评估量化

首先，基于开源入侵检测系统获取警报信息。然后，基于熵关联度计算各量化周期内的网络安全态势值。具体方法设计如下。

各周期网络安全态势量化值依据具有最高质量值的警报确定[10]。在C个量化周期内，Zi（i=1,2,…,C）为周期i的量化值，Qi为周期i内质量值最高的警报，则（i=1,2,…,C），其中，警报发生率（AO,alarm occurance）为

Qi的警报致变程度（AM,alarm mutagenicity）为，表示Qi引发网络安全状态变更的难易程度。越低，则变更难度越大。优先级设为1、2、3，分别对应警报Qi为周期i内发生、周期i−M至周期i−1 内发生和周期i−M至周期i−1 内未发生，本文取M=2[11]。

Qi的警报负面程度（AN,alarm negativity）为ANQi，该值越小，则网络安全状态受Qi影响程度越小。优先级设为3、2、1，分别对应警报负面程度为高危、中危、低危。

网络安全态势依据评价关联度矩阵R（如表1所示）量化。令，则Y1、Y2、Y3分别对应周期i内警报质量最高的警报Qi的3 个量化指标，即警报发生率、警报致变程度及警报负面程度。表1 中rij为第i个指标关联第j个评价（i,j∈{3,2,1}）的密切程度。

表1 评价关联度矩阵R

为区分指标Y1对网络安全威胁严重程度，设定警报发生率区间oj如表2 所示，基于Y1值和警报发生率区间端点偏离距离计算当前时刻Y1和区间oj（j=3,2,1）的相关度，该相关度即为Y1对表1 内各评价的关联度。

表2 警报发生率区间oj

设Y1=y，则特定指标与每个评价之间的关联度为

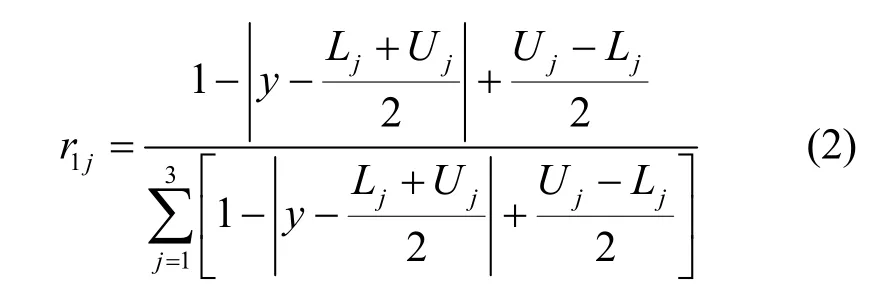
其中，Lj和Uj分别为oj的下端点和上端点，j=3,2,1。

由于指标Y2、Y3均根据优先级判定指标对网络安全威胁程度，故指标Y2、Y3对各评价的关联度设定如表3 所示。

表3 Y2、Y3 对各评价的关联度设定

表3 中，优先级越高，则指标威胁程度越大，故低优先级对评价高危、中危、低危的关联度递增，反之则递减。当指标Yi（i∈{2,3}）优先级为j时，取表3 与j同一行内的关联度作为表1 内Yi（i∈{2,3}）对应的关联度。警报各指标的绝对熵值为

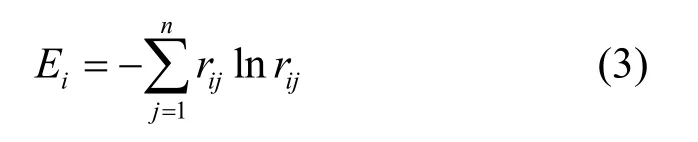
当ri1=ri2=…=rin时，Emax=lnn，则警报各指标的相对熵值为

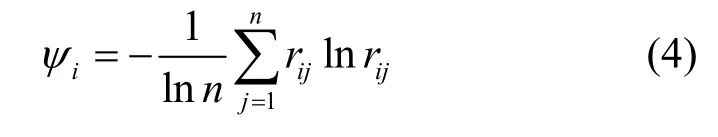
某指标相对熵值越大，则表示该指标对警报的量化值的影响越小，则以1−ψi表示对应指标的权值，即

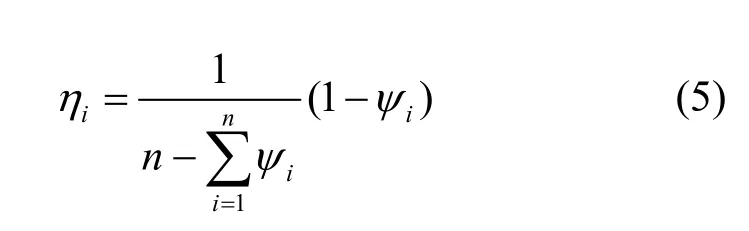
其中，ηi∈[0,1]为指标Yi的熵权系数，且η1+…+ηn=1。

各评价权值[12]为。

在第i个周期，计算得到其网络安全态势的量化结果[13]为

其中，态势放大系数ρ=10 000。态势量化值越高，则网络安全状况越差。

4 网络安全态势预测方法

通过自适应调整静态修匀系数α，使基于多重系数修匀法获取的初始预测结果精度较高。初始预测值计算步骤如下。

步骤1利用可变域空间划分以往数据时间序列片段。设W为域空间宽度，Z1,Z2,…,Zp（p为正整数）为当前网络安全态势评估量化值序列，可变域空间工作过程如下。

1) 定义当前域空间宽度内的态势值个数为l（1≤l≤p），则在该域空间内的该值的时间序列为Z1′,Z2′,…,Zl′。若l+1≤W，域空间位置固定，则计算第l+1 周期态势值，然后在域空间内输入下一个态势值。

2)若l+1>W，输入下一个态势值到以往序列中，并将域空间向后移动一个时间单位，以域空间内新态势值序列片段为对象，计算第p+1 个周期的态势值。

可变域空间的移动与取值变化如图2 所示。该机制保证多重系数修匀法所基于的时间序列长度不超过W，从而保证新的安全态势值加入以往序列后多重系数修匀法仍能正常预测，且可提高安全态势值预测的准确性与动态性。

图2 可变域空间的移动与取值变化

步骤2计算静态修匀系数。设当前网络安全态势值序列为Z1,Z2,…,Zp，域空间内态势值个数为l。若p≤W，则Z1′=Z1，Zl′=Zp；若p>W，则Z1′=Zp−W+1，Zl′=Zp。多重系数修匀法为

其中，周期t+X的安全态势量化预测结果为，预测周期提前量为X，dt、et、ft为周期t的预测系数。

其中，α∈[0,1]为静态修匀系数。

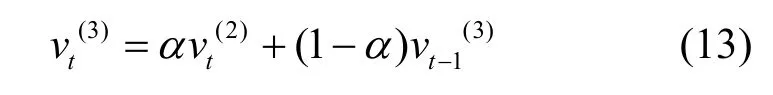
其中，Yt为周期t的真实态势值

在上述处理过程中，α的取值间接影响最终预测结果的准确性和精度。通常，当实际值序列呈水平趋势时，α∈[0.05,0.2]；当实际值序列存在波动，但长期波动较小时，α∈[0.3,0.5]；当实际值序列波动很大，呈明显的上升或下降趋势时，α∈[0.6,0.8]。α值越大，表明远期数据对预测值的影响越大。因态势实际值序列片段随可变域空间位置发生变化，本文通过最小化实际值和预测值的偏差绝对值之和求得α自适应解。α自适应解求解步骤如下。

1) 设当前可变域空间内的l个网络安全态势实际值组成向量Z′=（Z1′,Z2′,…,Zk′），静态修匀系数α初值为0。

3)设t=0,1,…,l−1，预测周期提前量X=1，由式(7)计算得到经α修匀的预测值序列Z1。

4)设预测值序列与实际值序列的偏差绝对值之和为V，则有

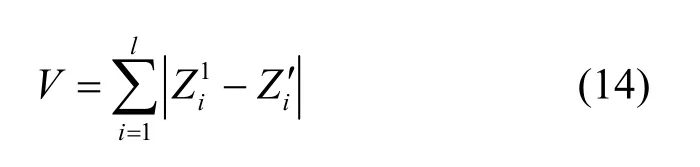
5) 循环1)～4)，若α=1，则转到步骤3；否则继续循环1)～4)。

设第j次循环后得到的偏差的绝对值为Vj，计算得到Vj最小值条件下的α值静态修匀系数自适应解为αa。

步骤3计算网络安全态势初始预测值。令t=l=p，α=αa，X=1，由式(7)～式(13)求得第p+1 个周期的安全态势值。

5 预测值的修正

通过网络安全态势预测子模块，得到可变域空间内各周期网络安全态势初始预测值。根据常识可知，该值与同域空间内的已知安全态势实际值存在偏差，且偏差大小与可变域空间内安全态势波动大小有关。本文将预测值与实际值偏差划分为若干偏差类别，并通过时变加权马尔可夫链预测偏差值。

5.1 偏差类别划分

处于不同时刻的网络所面临的漏洞、威胁将发生变化，可能出现如下的情况。

1)在短时间内网络遭受集中攻击，导致其安全态势出现较大波动，安全态势预测值与实际值偏差上、下限值距离较大。

2)网络面临常规漏洞，故其安全态势在一定时间内会较为平缓或出现较小波动，安全态势预测值与实际值偏差上、下限值距离较小。

新态势值加入以往序列引发可变域空间移动，改变可变域空间内态势值序列片段波动离散程度和最大、最小偏差距离。

设i=1,2,3,…,l，则当前域空间中的态势实际值片段为，态势预测值片段为，最小偏差值为，最大偏差值为，偏差距离为DL=DU−DL。划分偏差类别步骤如下。

步骤1划分偏差距离为k个区间，区间宽度为，区间元素为,。

步骤2设i=1,2,3,…,l，当前域空间内偏差时间序 列 为，若,，则偏差Di属于偏差类别j，j∈1,2,…,k。当Di=DU时，则可将Di划归为类别k。

步骤3若修正后的预测值不满足偏差检验等级要求，则偏差类别数k=k+1，使偏差修正细粒度化。

5.2 偏差预测方法

针对域空间内的偏差类别的样本，采用时变加权马尔可夫链模型对安全态势的偏差进行预测，具体步骤设计如下。

步骤1安全态势的偏差类别转移概率矩阵获取。假设当前安全态势的偏差类别为k个，当前时刻为x，相邻时刻偏差类别为dx−1dx，m个时刻后的偏差类别为dx+m，则有

其中，pa为偏差类别转移概率，a为时刻x−1 的偏差类别，b为时刻x的偏差类别，c为时刻x+m的偏差类别。

设k为偏差类别数，当k=3 时，转移概率矩阵为

其中，k=1,2,…,ϕ。ϕ值通过步骤3 调整，其初值由可变域空间宽度W确定，本文取。

步骤2确定偏差类别转移概率矩阵权值。首先计算dx−1dx和dx+m间的相关系数χq为

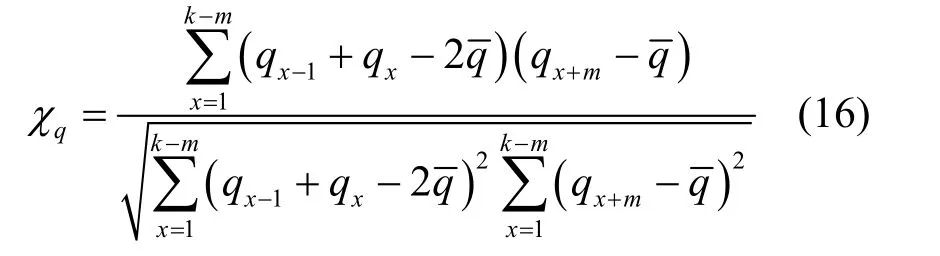
其中，qx−1、qx和qx+m分别为域空间内时刻x−1、时刻x和时刻x+m的偏差值，为域空间内偏差序列片段均值，m=1,2,…,ϕ。则m阶偏差类别转移概率矩阵权值μm为

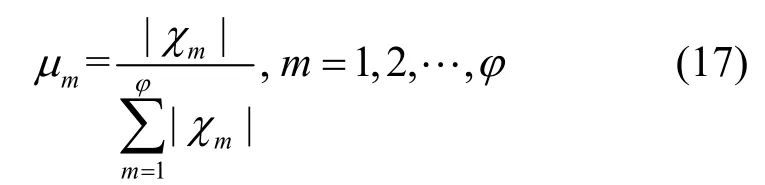
步骤3根据μϕ值调整ϕ值。当μϕ<0.05[14]时，去除对预测偏差作用较小的ϕ阶偏差类别转移概率矩阵，令ϕ=ϕ−1 并更新μϕ值，当μϕ≥0.05 时，取mmax=ϕ。

步骤4计算偏差预测值。x+1 时刻偏差值属于偏差类别c，c=1,2,…,k的概率pc(x+1)为

其中，m=1,2,…,ϕ；a,b∈{1,2,…,k}，根据m阶偏差类别转移概率矩阵Pm确定，表示由相邻偏差类别组dx−m=a、dx−m+1=b转移至偏差类别dx+1=c的概率。μm为m阶偏差类别转移概率矩阵权值，x+1时刻的安全态势预测偏差的类别概率分布向量为Pc(x+1)={p1(x+1),p2(x+1),…,pk(x+1)}。

设由各偏差区间中值组成的偏差中值向量为

则x+1 时刻偏差预测值算子为

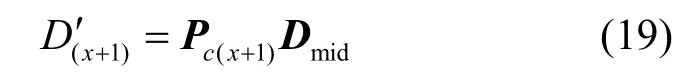
x+1 时刻预测值修正结果为

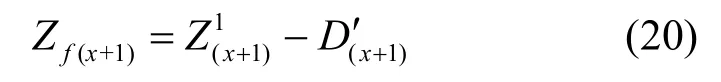
5.3 偏差检验

分析修正后的安全态势预测值与实际值的接近程度，从而判断偏差类别划分数量k是否足够。已知某域空间内的修正后的安全态势预测值序列与实际值序列如表4 所示。

表4 预测值序列与实际值序列

本文偏差检验方法介绍如下。

1) 后验差检验

残差Ri=Zi−Zf（i），i=2,3,…,l为实际值和经修正的预测值之差。当前安全态势序列片段内安全态势值方差S12为

残差序列方差S22为

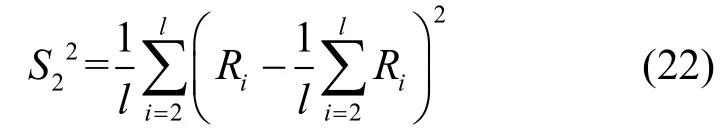
2) 小概率检验

小概率检验结果τ为

偏差检验等级如表5 所示。通过表5 判断是否需增加偏差类别划分数量。若偏差等级为1 级或2级，满足偏差等级检验要求，不需增加偏差类别数量，否则偏差类别数量为k+1。偏差等级小，表明预测的态势值结果偏差小。

6 实验与结果

6.1 实验场景

采用林肯实验室的标准数据集LL_DOS_1.0 验证本文模型的预测有效性。LL_DOS_1.0 攻击过程如下。

表5 偏差检验等级

1～70 min：攻击者安装相关攻击软件，并通过IP Sweep 扫描实验网络拓扑以寻找当前活跃主机。

70～125 min：利用Sadmind Ping 查找存在Sadmind 漏洞的主机。

126～240 min：攻击者利用Sadmind Exploit 攻击经70～125 min 锁定的3 台主机Pascal、Mill 和Locke 直至入侵各主机系统。

241～319 min：攻击者在受到入侵的3 台主机上安装DDoS 木马程序。

320 min 以后：攻击者对远程服务器发动DDoS攻击。

6.2 数据处理

在Ubuntu16.04 操作系统下，采用Tcpreplay 技术重放LL_DOS_1.0 数据分组，并在Windows10 操作系统下通过Snort 入侵检测系统针对重放流量生成告警日志。

基于第3 节网络安全态势评估量化方法生成态势实际值序列。将1～360 min 按时间间隔T=4 min 划分为90 个量化周期，各周期内的态势量化值区间为[2 800,4 000]。初始态势值序列由1～40 min 的10 个量化值组成，通过比较剩余的80个态势实际值与对应预测值拟合程度验证本文模型有效性。

以41～360 min 某40 min 时间段内的10 个安全态势值为例，说明本文模型预测过程。

某量化周期T=4 min 内的优选警报Q、警报负面程度ANQ级别、警报发生率AOQ级别和警报致变程度AMQ级别的属性如表6 所示。

表6 警报属性样例

依据式(2)及表1～表3，得到评价关联度，如表7所示。

表7 评价关联度

由式(2)～式(6)计算可得，该周期的网络安全态势量化值为Z=3 504，其他量化周期的量化过程在此不再赘述。则得到该40 min 时段内的10 个安全态势序列如表8 所示。

表8 安全态势序列

6.3 安全态势值的预测与修正

由第4 节网络安全态势预测方法获取T2～T10的安全态势预测值。设可变域空间宽度为W=10，得当前态势值序列下静态修匀系数自适应解αa=0.126，初始预测值与实际值对比如表9 所示，经计算得。

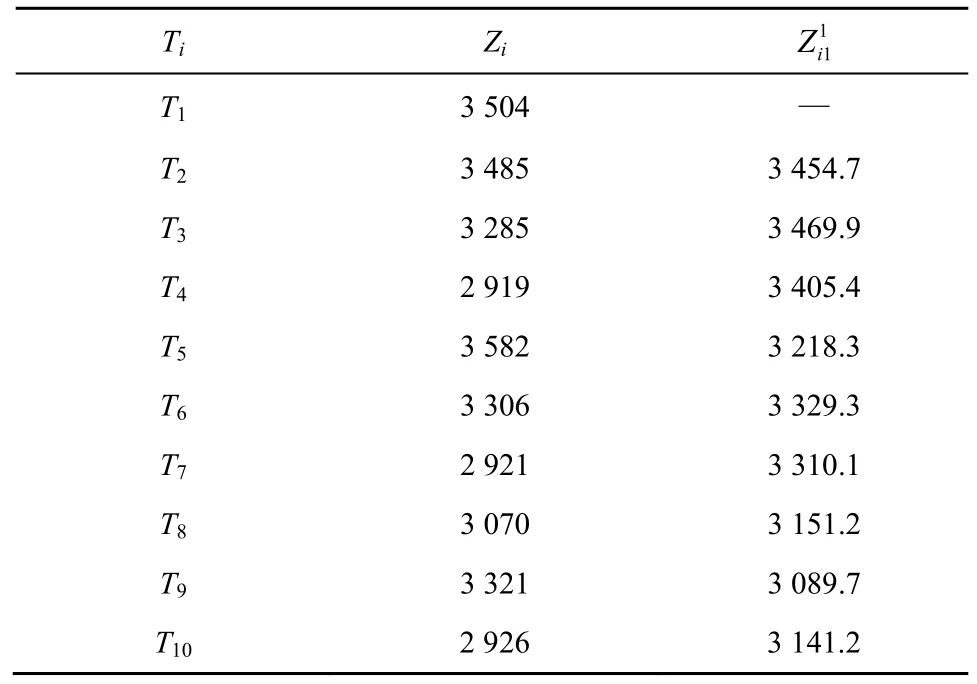
表9 初始预测值与实际值对比

T2～T10周期偏差序列如表10 所示，偏差区间[DL,DU]=[−363.7,486.4]。根据第5 节的预测值修正方法，当划分偏差类别数量k=8、ϕ=4 时，初始预测值修正后，可满足后验差检验与小概率检验条件。偏差类别区间如表11 所示。

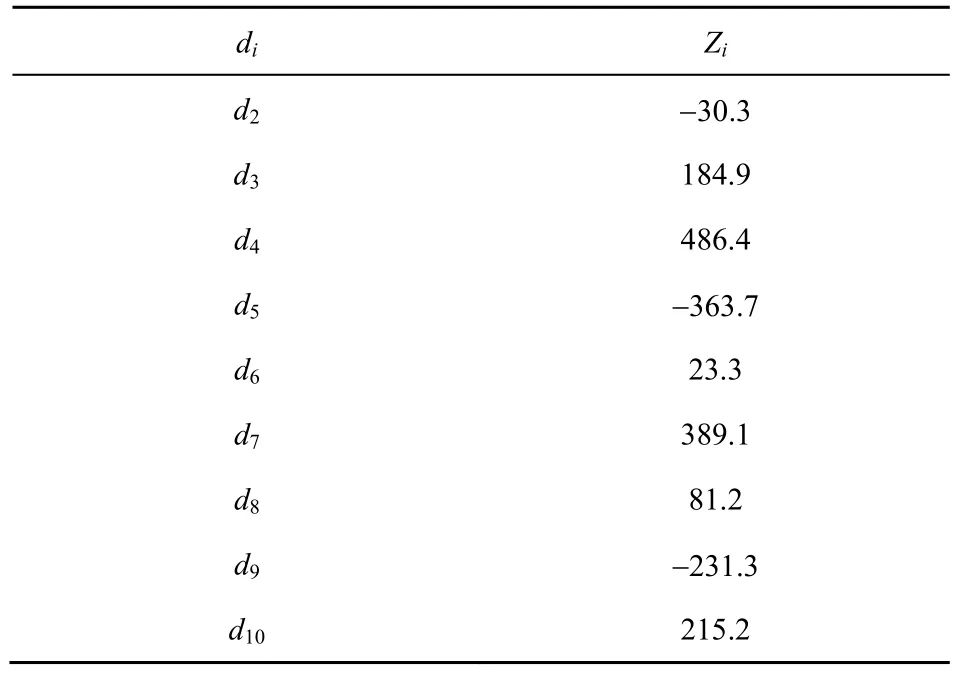
表10 偏差序列

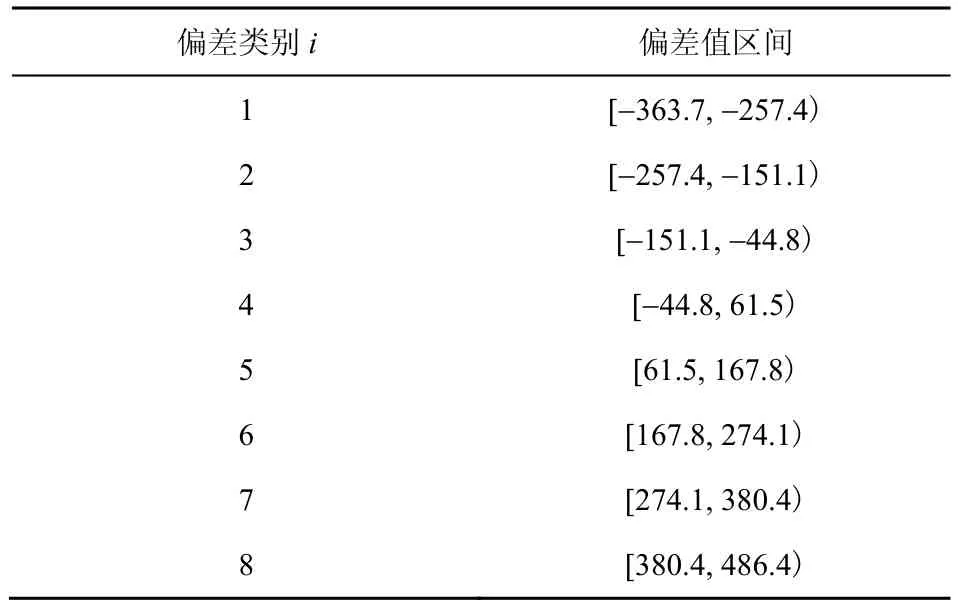
表11 偏差类别区间划分

由式(14)～式(19)计算得T2～T10修正后的安全态势预测值，其中偏差类别初始概率分布向量由在T1周期之前的10 个量化周期的安全态势值确定。安全态势预测修正值与实际值对比如表12所示。

表12 预测修正值与实际值对比

预测修正值Zf(i)序列的后验差比值θ=0.42，小概率检验结果τ=0.89。由表5 可知，该模型偏差等级为2 级，满足偏差检验条件，则T11的安全态势预测值为，与原态势序列中同周期的安全态势值Z11=2 920 的相对偏差为1.8%，表明该预测精度较高。

对于其他周期安全态势值的预测和偏差检验，重复6.2 节和6.3 节过程，共计生成80 个安全态势预测值。

6.4 最佳可变域空间宽度选取

静态修匀系数α自适应解受可变域空间内以往数据序列片段长度影响，改变初始预测精度。本文选取最佳可变域空间宽度以提高初始预测值和实际值的拟合程度。由于多重系数修匀法单次预测精度在15 个以往数据以内较高，故本文试用可变域空间宽度集合为{W|W=5,10,15}，不同域空间宽度下预测值对比如图3 所示。

图3 不同域空间宽度下预测值对比

由图3 可得，最佳可变域空间宽度为W=10，此时初始预测值精度更高。原因分析如下。

1) 当W=5 时，域空间宽度较小，以往样本数据片较短，最近样本数据的影响更加显著。

2) 当W=10 时，可变域空间宽度居中，以往样本数据段内异常波动数据和平缓波动数据的数量差距减小，远期、近期数据均衡影响安全态势预测，从而提高了初始预测值精度。

3) 当W=15 时，域空间宽度大，以往样本数据片较长，域空间内少量异常波动数据和其他平缓波动数据相比，对静态修匀系数自适应解影响作用更小，降低了态势突变处的初始预测值精度。

6.5 态势预测对比实验与分析

实验数据集为LL_DOS_1.0 数据集，分别采用本文模型、IFS-NARX 模型[9]和传统马尔可夫模型生成安全态势预测值序列，如图4 所示，安全态势预测值绝对偏差序列如图5 所示。

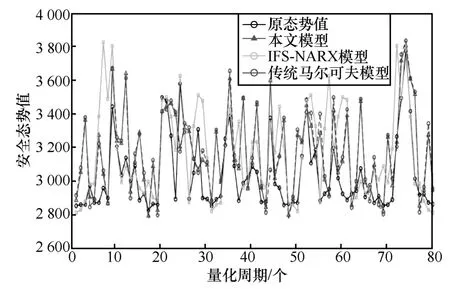
图4 安全态势预测值序列

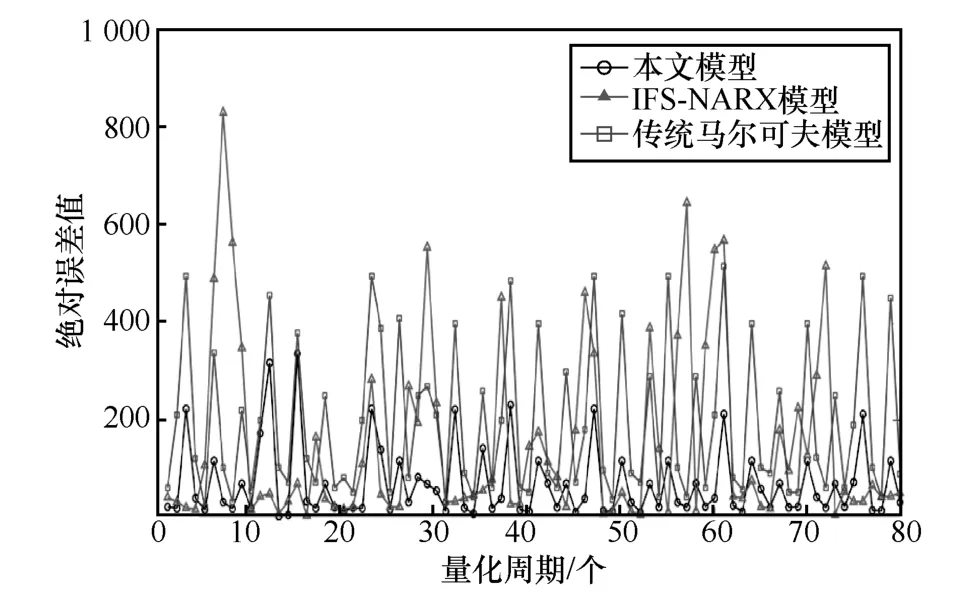
图5 安全态势预测值绝对偏差序列

从图4 和图5 可知，由本文模型获取的态势预测结果更加符合原始的网络安全态势情况，绝对偏差更小。原因分析如下。

1) 传统马尔可夫状态转移概率矩阵随以往数据增加而收敛，故传统马尔可夫模型面向较短时间序列预测效果理想，当时间序列较长时，绝对偏差增大且偏差峰值周期性出现。

2) 将警报发生率、警报致变程度和警报负面程度作为IFS-NARX 模型输入特征，非线性自回归神经网络参数由经验公式确定，该模型面向短序列预测因样本数量较少而预测精度不佳，当序列长度增加时，样本数量提高，模型预测精度提升。

3) 本文模型中，可变域空间位置随新态势值加入以往序列而发生移动，更新域空间内态势序列片段，调整静态修匀系数自适应解取值、偏差类别划分数量和偏差类别转移概率矩阵，使预测精度在不同长度时间序列下保持较高水平。

7 结束语

本文提出一种基于自修正系数修匀法的网络安全态势预测模型。通过熵关联度量化若干周期的网络安全态势值，采用可变域空间机制对按时序排列的安全态势值进行片段化处理，运用自适应多重系数修匀法初步生成安全态势预测结果，运用时变加权马尔可夫链对偏差进行预测并修正安全态势预测值。实验结果表明，本文模型预测自适应性较强，预测精度较高。下一步主要分析态势序列线性性质并将长短期记忆网络模型和动态信誉机制[15]、安全规则集合[16]相结合，以提高本文模型对态势突变处的适应性。