基于改进的免疫克隆蛙跳算法的多约束QoS 路由优化研究

卢毅，徐梦颖，周杰

（石河子大学信息科学与技术学院，新疆 石河子 832003）

1 引言

随着无线通信技术的迅速发展，无线传感器网络（WSN,wireless sensor network）已成为研究热点之一。由于其低能耗、低成本、数据存储能力强、无线通信能力强、自组织等特点，WSN 的应用领域越来越广，包括智能家居、交通、农田监测等[1]。

无线传感器网络由众多具备信号传输与计算性能的传感器节点通过自组织网络的形式构成，其主要特点是以数据为中心，且具备一定的网络规模与拓扑结构以满足感知信息的传输、处理、存储、显示、记录和控制要求[2-3]。在农业方面，WSN 主要应用于温室大棚的温湿度采集控制、节水灌溉、土壤pH 值测量、动植物种群复杂度的监测等。

服务质量（QoS,quality of service）优化是无线传感器网络单播路由优化中待解决的一项难题，该问题是一个NP 完全问题，传统的算法在优化该问题时效果并不理想[4-5]。研究人员希望有限的无线传感器网络能量能够被网络系统高效使用，使数据在链路中的传输能耗最小，同时不影响传输链路的其他指标。这也是单播路由优化问题中的一个重要任务。然而，QoS 受许多因素的影响，包括时延、链路带宽、时延抖动、分组丢失率等[6-8]。实时无线通信过程中数据的传输受到上述因素的限制，可能会影响用户的视觉体验和听觉体验[9]。无线传感器网络可以抽象为图论中的有向图，节点与节点之间存在许多链路。链路上的数据受时延、链路带宽、时延抖动、分组丢失率的影响，源节点与终端节点之间存在多条可行路径，所以优化的目的是在满足以上约束条件的前提下找到一条能量损耗最小的路径。

在过去的研究中，研究人员通过多种智能仿生算法解决和优化上述问题，例如遗传算法（GA,genetic algorithm）、蚁群优化（ACO,ant colony optimization）算法、粒子群优化（PSO,particle swarm optimization）算法等[10-12]。文献[13]提出了一种用于单播多约束优化的遗传算法，但是在算法的迭代过程中，交叉和变异步骤没有进行改进，产生的路径极可能为不可行路径，从而无法找到有效解。文献[14]提出一种蚁群优化算法进而优化带约束的服务质量路由问题，但是该算法计算复杂度较高。在无线传感器网络中，为了保证服务质量，路径要满足传输损耗最小的条件，同时保证通信质量。文献[15]提出了一种改进的萤火虫算法用于保证电力通信，该算法用于优化网络链路带宽、时延和分组丢失率，通过混沌编码提高种群的多样性，实验结果表明，该方法有效地优化了网络资源，能够找到一条满足电力通信业务的有效路由。针对多约束条件下的路由选择问题，文献[16]提出了一种新的路由选择算法，该方法在萤火虫算法的基础上结合了量子进化算法，有效解决了无线路由协议中的路由选择问题，但随着问题规模的增加，计算时间大大增加。

蛙跳算法（SFLA,shuffled frog leaping algorithm）是近年来被提出的仿生学优化算法，它具备概念简单、参数极少、计算速度快、优秀的全局搜索能力、实现简便等优点[17-19]。SFLA 自从被提出之后就受到普遍关注，现已经应用于水资源节能灌溉、电线电缆的排序等领域。SFLA 通过种群编码、种群初始化、计算适应度、子种群划分、局部搜索和全局搜索来提高求解质量。在算法操作过程中，种群被分为几个子种群，不同的子种群具有不同的信息，对每一个子种群进行局部搜索，通过子种群的进化求优化解，经过一定时间的进化和跳跃过程，最后进行全局搜索，直到收敛或者达到标准。

为了优化QoS 单播路由问题，本文建立了数学模型，路由选择需要满足传输路径上产生的时延抖动、分组丢失率、时延、链路带宽等限制条件，在此基础上找到一条数据从源节点出发到终端节点间所需能量损耗最低的路径。为了找到最优路径，本文提出了一种改进的免疫克隆蛙跳算法（IICSFLA,improved immune clonal shuffled frog leaping algorithm），该算法结合了传统蛙跳算法与免疫克隆算法的优点。对于优化复杂问题，所提算法可以加快算法收敛速度，并避免局部最优，在搜索过程中通过结合变异算子不断向最优解靠近，保证了算法的稳健性、收敛性、自适应性。在仿真实验中，将改进的免疫克隆蛙跳算法的性能与自适应遗传算法和自适应蚁群算法的性能进行了对比，仿真结果显示，所提算法有效地降低了数据在传输路径上的能耗，同时满足了其他多项约束条件。

2 系统模型

本节介绍多条件限制的QoS 单播路由优化模型。无线传感器网络的图论模型可以看作一组传感器的节点集合和节点之间的链路集合，用G(V,E)表示。用图论方法表示源节点、终端节点、多个中继节点和链路时，节点集合包括源节点v1、终端节点vn和多个中继节点v2→ …→vn−1，源节点为第1个节点，中继节点为第2～第n−1 个节点，终端节点则为第n个节点。从源节点至终端节点的链路可以表示为p(v1,vn)={v1→v2→ …→vn}。

每一段链路都由2 个节点构成，假设相邻的2 个节点序号为i和j，e={vi→v j}(i≠j)。数据在每条链路上的传输情况都受到时延抖动、分组丢失率、时延、链路带宽这4 个参数的限制。每条链路上的能量损耗为C(e)，抖动为D(e)，链路带宽为B(e)，时延抖动为D_J(e)，分组丢失率为P_L(e) 。

2.1 能量损耗模型

在2 个相邻节点i和j之间的链路上，能量损耗由传输数据能量和接收数据能量构成，则2 个相邻节点间的总能量损耗C(e) 为

其中，Cs为2 个相邻节点间的传输数据所消耗的能量，Cr为2 个相邻节点间的接收数据的能量。

当2 个相邻传感器节点之间的距离为l，传输数据量为k时，传输数据能耗为

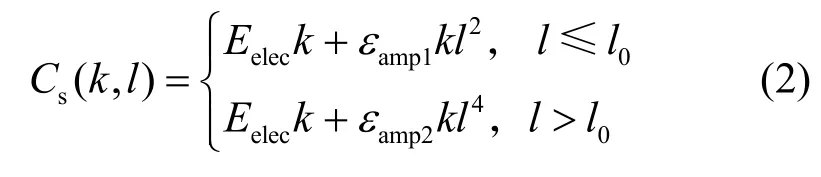
其中，l0为2 个相邻传感器节点之间的距离阈值传输数据，Eelec为电能参数，放大器能量由功率放大参数εamp1决定，路径上能量衰落由εamp2决定。本文设Eelec=50 nJ/bit，εamp1=10 nJ/(bit ⋅m2)，εamp2=0.015 nJ/(bit ⋅m4)，l0=1m。

当接收数据量为k时，需要的能量Cr(k)为

当2 个传感器节点相距0.5 m，k=1 Mbit 时，由式(3)计算可得Cr(k)=Eeleck=50 nJ/bit ×106bit=0.05 J 。

2.2 路径参数

1) 能量损耗函数

数据从节点v1传输到节点vn时，链路p(v1,vn)的能量损耗为

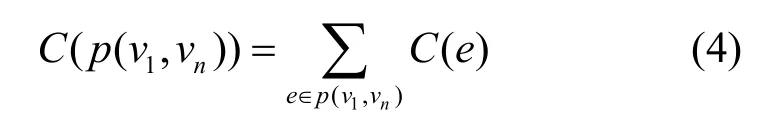
2) 时延函数

数据从节点v1到节点vn产生的总时延为

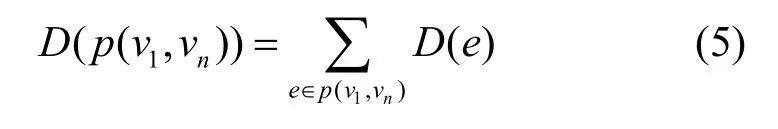
3) 链路带宽函数

数据从节点v1到节点vn产生的总链路带宽为

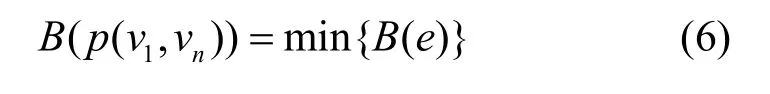
4) 时延抖动函数

数据从节点v1到节点vn产生的总时延抖动为

5) 分组丢失率函数

数据从节点v1到节点vn产生的总分组丢失率为

2.3 目标函数

在无线传感器中，多条件限制的QoS 单播路由模型可以由图模型构成。假设该图中有V个传感器节点、E条链路，则该图可以表示为G(V,E)，在相邻节点的链路上将受时延、链路带宽、分组丢失率、时延抖动、能量损耗的影响。基于这些限制条件，QoS 单播路由问题的目标函数为找到一条从源节点至终端节点数据传输所需的能量损耗最低的路径。

适应度（fitness）是依据生物对于大自然生存环境的适应程度，针对事件中所有个体呈现出的不同表现的一种监测方法。适应度函数即实际问题中的所有基本单位与其自身适应度的一一对应关系，通常情况下它是一个常量函数。用fitness 表示能量损耗对应的适应度，目标函数如式(9)所示。

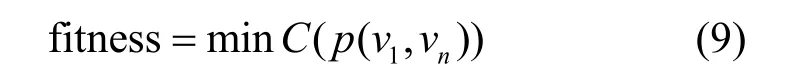
2.4 约束条件

该模型是为了找到一条能量损耗最小的最优路径，由源节点v1开始传输数据，直到终端节点vn结束数据的传输，这条路径上的各个相邻节点间的分链路需要满足以下条件。

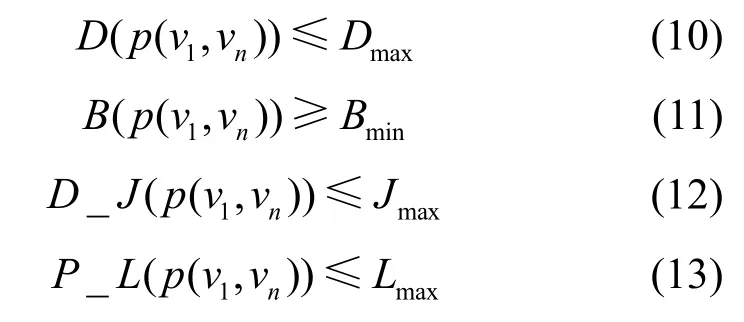
其中，Dmax为链路上所能接受的最大时延，Bmin为链路上的最小链路带宽，Jmax为链路上所能接受的最大时延抖动，Lmax为最大分组丢失率。

3 QoS 路由优化算法设计

蛙跳算法是受青蛙捕食行为的启发而提出的优化算法，该算法综合了变异算子的搜索特点，拥有较好的搜索解的能力。传统的蛙跳算法包含以下几个步骤[20-21]：种群编码、种群初始化、计算适应度、子种群划分、局部搜索、全局搜索。

针对多条件限制的QoS 单播路由优化问题，本文提出一种改进的免疫克隆蛙跳算法优化QoS 路由，该算法结合了免疫克隆算子的优点，克服了早熟收敛的缺点，维持了抗体种群的多样性。

II CSFLA 的主要思路如下。任意生成N只青蛙构成一个最初部落种群，X={X1,X2,…,Xi,…,XN}，D维空间中的第i只青蛙可以表示为Xi={xi1,xi2,…,xiD}。假设初始蛙群可分为I个子种群，每个子种群中有J只青蛙，则初始部落种群与子种群之间满足N=IJ。产生最初部落种群以后，首先把部落种群内青蛙按照规定的适应度升序排列。在QoS 路由选择优化问题中，青蛙按照从源节点到终端节点间的能量损耗由小到大排序，并且记青蛙种群中具备最低能耗的青蛙个体为Xg_min。例如，当种群FROGS 中有40 只青蛙，每只青蛙代表路由能耗时，适应度升序排列仿真内容和仿真结果如图1 所示。

由图1 可以看出，经过排序个体按照从源节点到终端节点间的能量损耗由小到大依次排序，在1号位置的青蛙能耗最小。

其次把全部青蛙种群分成子种群，记录下每个子种群中能耗最小的青蛙Xb_min和子种群中能耗最大的青蛙Xb_max。首先对子种群进行局部搜索，若改进后的青蛙较原来子种群中的青蛙更优异，那么改进后的青蛙将替代子种群中的原始青蛙。例如，在局部搜索过程中，种群中的40 只青蛙被分成4 个子种群，每个子种群10 只青蛙，则一次局部搜索的仿真结果如图2 所示。

如图2 所示，局部搜索后子种群中能耗最大的青蛙（能耗为0.734 2 J）被改进，得到的新青蛙能耗降为0.703 2 J。

如果没有任何优化，则随机选取一只新的青蛙来替代部族中原始的青蛙，反复进行上述局部搜索操作genmax次，直至完成局部搜索所有操作指令后，将经过上述操作的所有子种群内的青蛙重新组合并排列顺序，再实行全局搜索操作。如此重复操作，直至达到规定的收敛要求，从而达到全局变量最优化的目的。

3.1 种群编码

在多条件限制的QoS 路由优化问题中，数据传输的路径表示为

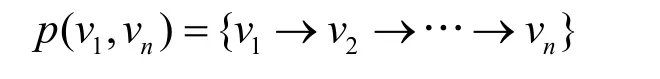
假设有n个传感器节点，节点的最大出度个数设为Smax，则每个个体的基因位长度T等于所有节点最大出度个数的对数的向上取整值，如式(14)所示。

图1 适应度升序排列仿真内容和仿真结果

图2 局部搜索仿真结果

数据由节点vi传向相邻节点vj时，(e={vi→v j}(i≠j))，两节点之间路径上的二进制编码取决于节点的出度。当某一传感器节点的出度为1 时，表示由该节点引出的链路个数为1，即可选择的路径只有一条。当传感器节点的出度为2 时，表示由该节点引出的链路个数为2，即可选择的路径有2 条，通过采用二进制编码表示路径的选择，一条路径用0 编码，则另外一条路径用1 来编码。例如，当传感器节点的出度为4 时，用2 个二进制比特位来表示路径的选择，分别是00、01、10、11。将基因位上的二进制数转换成十进制整数，然后根据该十进制整数选择链路。如果其超过了当前节点的出度的最大值，则算法取整除出度所得的余数作为链路编号。如果在个体上的所有基因位之前完成了链路选择，则剩下的基因位将忽略不计。最后将个体的二进制编码转化为由节点序号组成的路径p(v1,vn)，通过该方式生成一条路径。

3.2 种群初始化

在D维空间问题解的集合，随机产生N只青蛙（问题的解）为最初的部族，初始种群可以表示为X={X1,X2,…,X,…,XN}，第i只青蛙表示为，将青蛙种群按照数据在传输链路上产生的能量损耗的适应度排序，选取出能量损耗最低的青蛙编码为Xg_min。

3.3 计算适应度

多条件限制的QoS 单播路由选择优化问题中，在满足时延、链路带宽、分组丢失率、抖动时延条件的情况，适应度函数可通过式(9)计算，从而得出种群中每一只青蛙在数据传输过程中产生的能耗，能耗越小，说明青蛙被遗传到下一代的可能性越高。

3.4 子种群划分

将全体青蛙群体分为J个子种群，每个子种群中有I个青蛙个体，子种群按照以下规则划分：第1 只青蛙属于第1 子种群，第2 只青蛙属于第2 个子种群，第3 只青蛙属于第3 个子种群，第J+1 只青蛙放入第1 个子种群,第J+2 只青蛙放入第2 个子种群，依次类推，直至所有子种群中都有I只青蛙。记录每个子种群中能耗最小的青蛙Xb_min和能耗最大青蛙Xb_max。

3.5 局部搜索

局部搜索仅针对子种群内的青蛙进行更新。针对每个子种群，找到子种群中数据传输能耗最高的个体Xb_max，个体的更新方式如式(15)和式(16)所示。

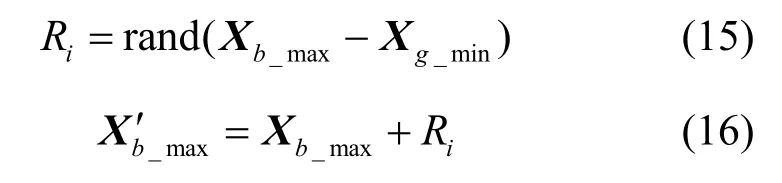
其中，rand 为0～1 的随机小数，Xb_min为子种群中能耗最小的青蛙，Xb_max为子种群中能耗最大的青蛙，Ri为青蛙的步长，每一步的步长不能超过最大步长，即−Rmax≤Ri≤Rmax。

若更新后的适应度小于子种群内的最优适应度，则用更新后的个体取代当前最差个体，若没有任何优化，则随机任意选取一个新的青蛙代替部族中原始的青蛙，反复进行上述局部搜索操作genmax次，genmax为子种群的最大迭代次数。

3.6 全局搜索

经过局部搜索后，重新计算更新后的所有青蛙个体的数据传输链路能耗，并由小到大进行排序。例如，当种群中有40 只青蛙，每只青蛙代表路由能耗时，一次全局排序的仿真结果如图3 所示，方框中数字为局部搜索新生成的青蛙能耗。

将全局能耗最低的个体设为Xg_min，该青蛙作为全局最优青蛙保存在每一代中，全局最差青蛙为Xb_max，全局搜索针对整个种群的最差适应度个体进行更新，全局更新式如式(17)和式(18)所示。

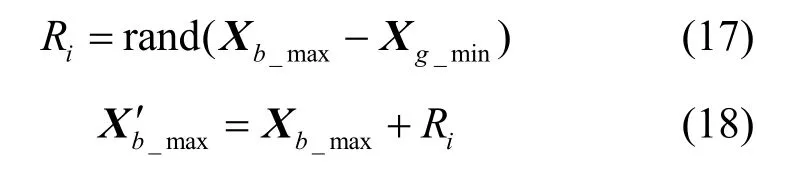
3.7 克隆免疫算子

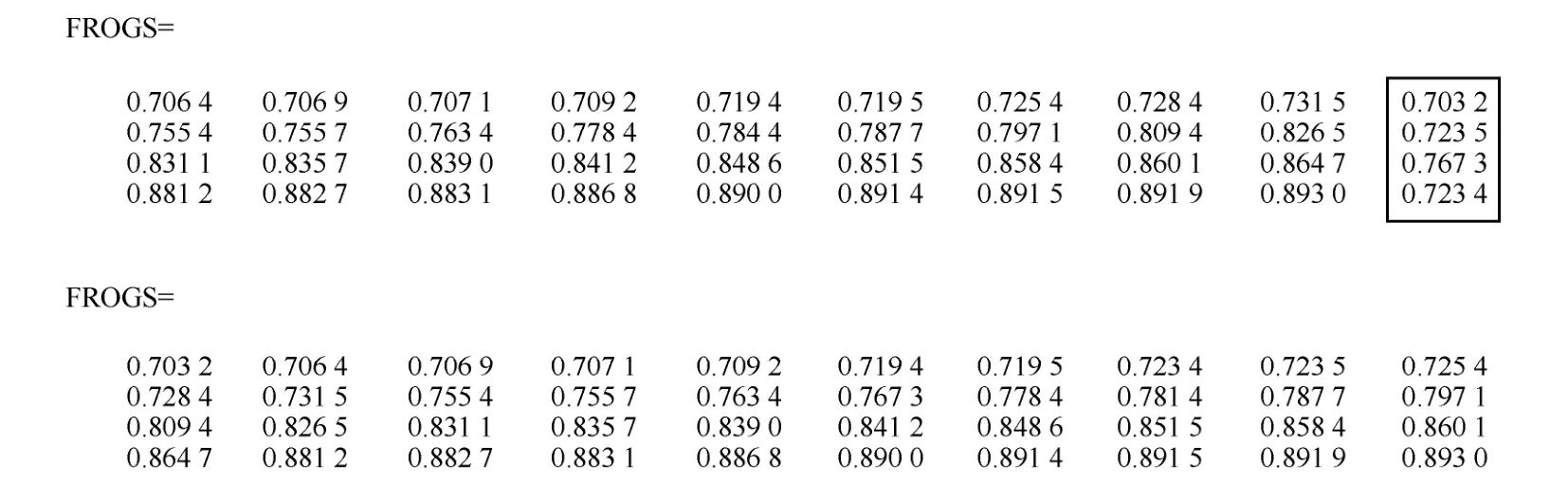
图3 全局排序仿真结果

免疫克隆算子是结合免疫生物学说与抗体克隆的优势而提出的一种新型算子。在免疫克隆算子中，一个抗体对应QoS 路由优化问题的一个可行路径，适应度对应路径上的能量损耗。该算子有效保证了种群的多样性，并保证算法有效收敛。例如，当种群中最优青蛙（能耗为0.706 4）被克隆变异10 份后，一次仿真结果如图4 所示。

由图4 可以看出，克隆变异后部分青蛙能耗低于原青蛙，而部分青蛙则高于原青蛙。

3.8 算法流程

IICSFLA 算法具体流程如下。

步骤1算法参数的初始化。初始化青蛙的种群大小N，搜寻空间的维数为D，子种群数为J，每一组子种群中包括I只青蛙(N=IJ)，每一个青蛙个体的位置变化最大值（步长）为Rmax，局部查找的次数为genmax，全局变量的迭代周期为MAXGEN。

步骤2青蛙群体的编码及初始化。随机产生一个由N只青蛙个体构成的原始部族。

步骤3将个体的二进制编码转化为由节点序号组成的路径p(v1,vn)。

步骤4计算适应度。通过式(9)计算适应度函数值，将青蛙群体按照适应度升序依次排列，选取并记录具备最低能耗的青蛙个体。

步骤5克隆种群中路径损耗最低的二进制个体，如果找到好的二进制个体，用该个体更新种群中最优个体。

步骤6子种群的产生。将N分割成J个子种群，每个子种群均包括I个个体，将子种群的个体按照适应度由小到大排序，并进行个体与子种群间的公平分配，选取并记录具备最佳适应度及具有最差适应度的青蛙个体。

步骤7子种群的进化（局部搜索）。针对子种群中选取出的最差个体，让其按照蛙跳算法规则实行局部搜索操作，新的位置改进取决于式(16)，经过计算，得出其青蛙个体的适应度。记录改进后的青蛙部族子种群中最差个体与最优个体。

步骤8子种群的重新混合（全局搜索）。将进化后的子种群中的青蛙群体进行重新组合，对新的种群集合依据其适应度升序排列，选出最优与最差个体，并对最差个体通过式(17)与式(18)进行更新。

步骤9算法结束条件。若达到最大迭代次数，结束更新蛙群，并输出最优解；否则，返回步骤3。

4 仿真与实验

仿真实验通过MATLAB 2012a 完成。假设一个区域范围内有20 个传感器节点，数据通过这些节点进行传输，数据在相邻节点间传输将会受时延、时延抖动、分组丢失率、链路带宽的影响。假设Eelec=50 nJ/bit，εamp1=10 pJ/(bit ⋅m2)，εamp2=0.0015 pJ/(bit ⋅m4)，k=1Mbit，d0=1m。设最大时延为105 ms，最小链路带宽为8 Mbit/s，最大时延抖动为36 ms，最大分组丢失率设为1%。

在仿真中，将IICSFLA 和自适应遗传算法（AGA,adaptive genetic algorithm）、自适应蚁群优化（AACO,adaptive ant colony optimization）算法进行对比，AGA 和AACO 的参数的初始设置根据经验获得，并在算法运行过程中自适应调整，3 种算法的迭代次数为100 次，参数如表1～表3 所示。

表1 IICSFLA 初始参数

表2 AGA 初始参数

表3 AACO 初始参数

在QoS 单播路由问题中，在多约束条件下找到一条从源节点到终端节点间所需能量损耗最低的路径。在优化数据传输的链路时，能量损耗作为优化目标，时延、分组丢失率、链路带宽、时延抖动只作为约束条件，且必须保持在约束条件以内。

图4 免疫克隆算子仿真结果

在传输数据之前，所有节点都处于休眠状态，此时不消耗能量，根据传感器的链路带宽、时延、分组丢失率、时延抖动的条件限制找到一条能量消耗最小的路径，并将该路径上的节点设为开启状态，此后数据的传输皆在此路径上进行。

图5～图8 分别对比了基于IICSFLA、AGA、AACO 的链路带宽、时延、时延抖动和分组丢失率。可以看出，3 种算法链路带宽皆大于最小带宽，时延均小于最大时延，时延抖动均小于最大时延抖动，分组丢失率均小于最大分组丢失率。

图5 为3 种算法的链路带宽对比。在路由过程中，链路带宽越大通信质量越好。可以看出，3 种算法迭代后的链路带宽均大于最小链路带宽8 Mbit/s，经过IICSFLA 迭代后的链路带宽为9.066 Mbit/s，AGA和AACO 迭代后的链路带宽分别为8.809 Mbit/s和8.624 Mbit/s，即经过IICSFLA 迭代后的链路带宽最大。

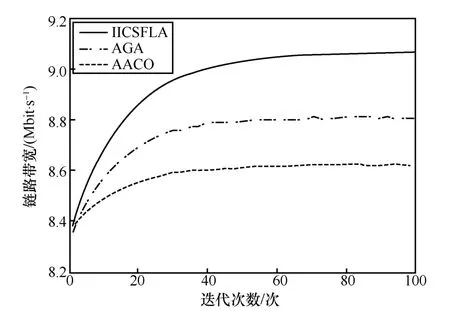
图5 链路带宽对比

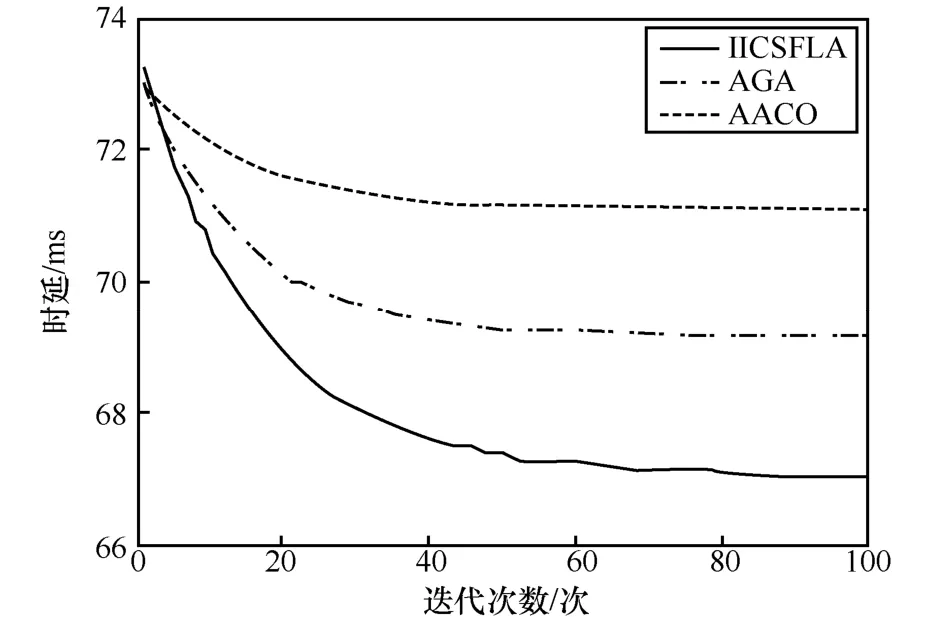
图6 时延对比

图6 为3 种算法的时延对比。在路由过程中，时延越小通信质量越好。可以看出，3 种算法迭代后的时延均小于最大时延为105 ms。IISFLA 迭代后时延最小，为67.05 ms；AGA 和AACO 迭代后时延较大，分别为69.16 ms 和71.06 ms。

图7 为3 种算法的时延抖动对比，时延抖动越小通信质量越好。3 种算法迭代后的时延抖动均小于最大时延抖动36 ms。IICSFLA、AGA、AACO迭代后的时延抖动分别为19.04 ms、21.17 ms 和23.06 ms，即IICSFLA 迭代后时延抖动最小。

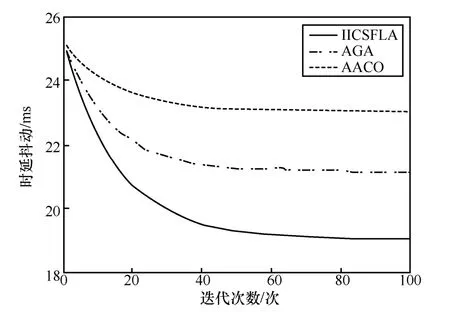
图7 时延抖动对比

图8 为3 种算法的分组丢失率对比。3 种算法迭代后的分组丢失率均小于最大分组丢失率1%。IICSFLA、AGA、AACO 迭代后的分组丢失率分别为0.230 5%、0.252 6%和0.271 1%，即IICSFLA 迭代后的分组丢失率最小。

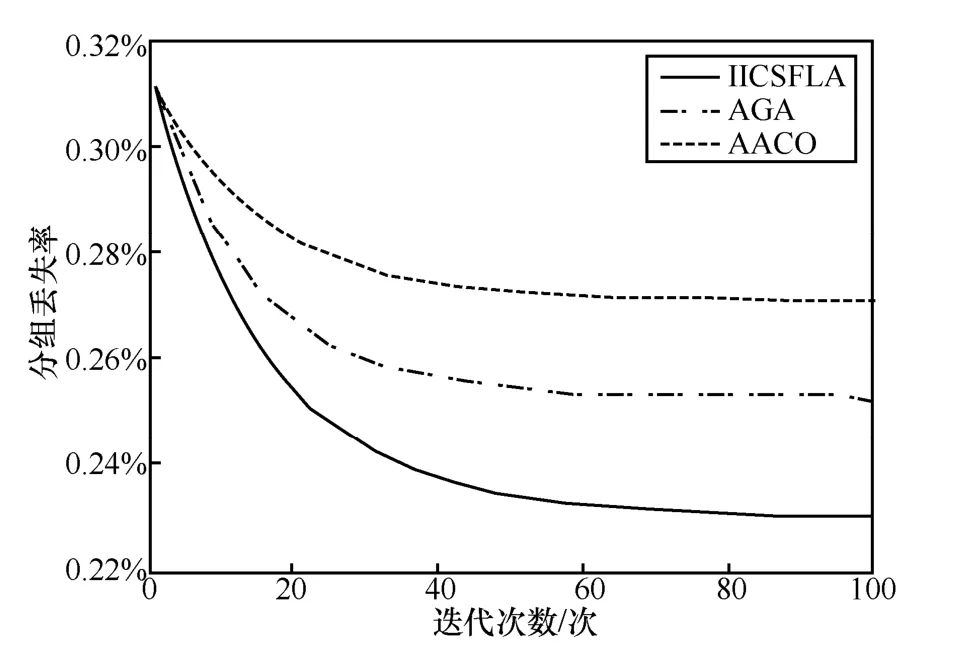
图8 分组丢失率对比

图9 为节点数量为20 时，3 种算法在迭代100次后的能耗对比。由图9 可知，当传感器节点数量为20 时，100 次迭代后IICSFLA、AGA、AACO的能耗分别为0.662 2 J、0.692 2 J 和0.716 6 J，AGA 和AACO 能耗比IICSFLA 分别高出4.53%和8.22%。由此可知，IISFLA 在加入了克隆免疫算子后，将能耗较低的青蛙个体当成记忆细胞以较大的概率保留到下一代种群中，相反，能耗较高的青蛙个体被遗传至下一代的概率较低。在时延、分组丢失率、链路带宽、时延抖动都满足条件的情况下，能够有效找到一条能耗最低的路径，体现了强稳健性，也提高了算法的收敛速度。

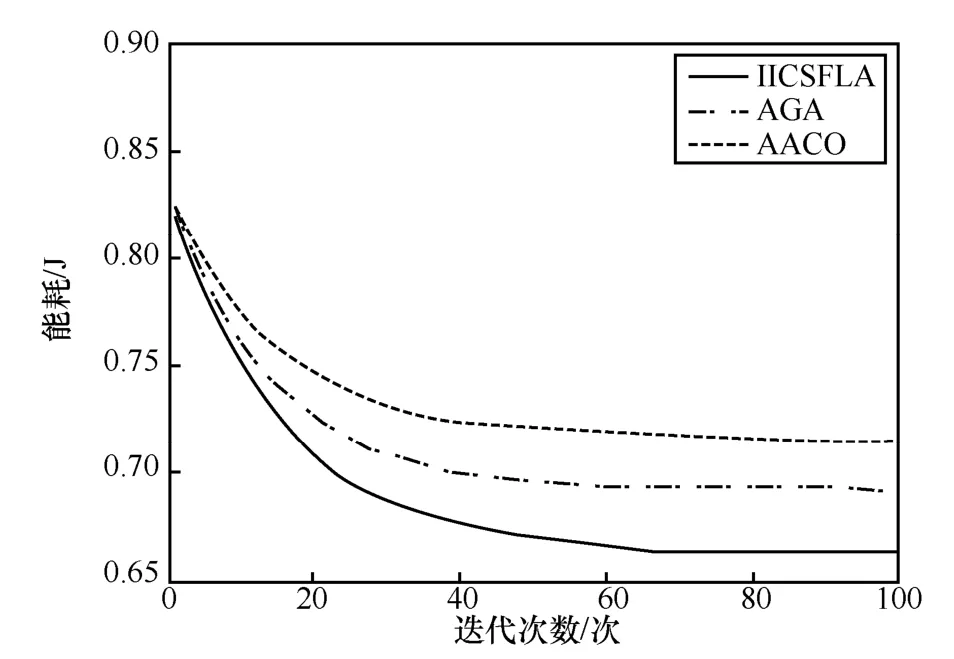
图9 节点数为20 时的能耗对比

图10 为节点数量为30 时，3 种算法在迭代100次后的能耗对比。由图10 可知，当传感器节点数量为30 时，100 次迭代后IICSFLA、AGA 和AACO的能耗分别为0.851 7 J、0.889 2 J 和0.9237 J。初始参数不变的情况下，AGA 和AACO 比IICSFLA的能耗分别高出4.40%和8.45%。

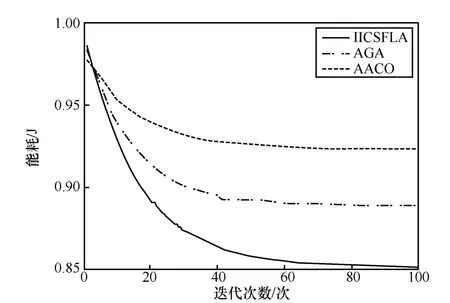
图10 节点数为30 时的能耗对比

图11 为节点数量为40 时，3 种算法在迭代100次后的能耗对比。由图11 可知，当传感器节点数量为40 时，IICSFLA、AGA、AACO 在100 次迭代后的能耗分别为1.304 J、1.370 J、1.429 J。100 次迭代后的AGA 和AACO 能耗比IICSFLA 分别高出5.06%和9.59%。

由上述仿真结果可知，混合免疫克隆算法的IICSFLA 具有更强的全局搜索能力，有效降低了路径上的能量损耗。

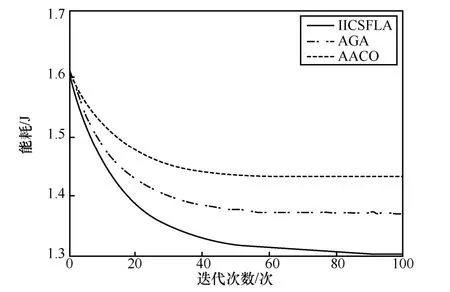
图11 节点数为40 时的能耗对比

5 结束语

针对多条件限制的QoS 路由优化问题，本文首先设计了系统模型，在时延、链路带宽、分组丢失率、时延抖动这些条件的限制下，计算数据在传输链路上的能量损耗。为了优化路由选择，提出了一种改进的免疫克隆蛙跳算法，该算法结合了传统蛙跳算法和免疫克隆算法的优点，在对IICSFLA 进化过程中，进行种群编码、种群初始化、种群划分、局部搜索、全局搜索，通过加入克隆免疫算子，将能耗较低的青蛙个体以较大的概率遗传至下一代抗体群，使进化后的SFLA 具备更加全面的全局搜索的能力。在仿真中，将所提算法与AACO与AGA 进行对比，结果显示，所提算法具有更快的收敛速度，能更有效地找到一条能耗最小的传输路径。