基于引导滤波和自适应容差的图像去雾算法
2020-06-06金仙力张威刘林峰
金仙力,张威,刘林峰
(南京邮电大学计算机学院,江苏 南京 210023)
1 引言
近年来,计算机视觉系统在智能驾驶、人脸识别、交通检测等领域已得到广泛应用。然而,雾霾天气下得到的图像往往会出现对比度下降、色彩失真、可视性下降和细节模糊等图像降质问题。图像降质对计算机视觉系统的目标识别和特征提取等后期处理过程产生了极大影响。因此,对图像进行有效的去雾具有重要的研究价值。
在雾霾天气下,受到大气中杂质分子的影响,拍摄图像存在严重的降质现象,许多细节信息丢失,这种现象在景深较大区域尤其明显。如图1(a)所示,近景处水面上的鹅虽然也变得模糊,但是相对来说可以看清,而景深处人物和树木则几乎完全被雾霾掩盖。经过对大量带雾图像的灰度直方图进行研究,如图1(b)所示,其中,纵坐标表示灰度值,横坐标表示灰度值对应的像素点的个数。相较于晴朗天气下拍摄的图像,雾霾天气拍摄的图像灰度值分布集中,这说明雾霾天气拍摄的图像的大量有效信息丢失,且图像的色彩会变得不够丰富。

图1 雾霾天气拍摄的图像及其灰度直方图
当前主流去雾算法可分为两类,一类是基于非物理模型的去雾算法,另一类是基于物理模型的去雾算法。常见的基于非物理模型的去雾算法,有全局、局部直方图均衡化算法[1]以及基于Retinex 原理[2]的去雾算法,此类基于非物理模型的去雾算法均是从带雾图像本身出发,并没有分析雾霾天气下图像出现退化的原因,因此在去雾的过程中,图像会损失大量细节信息[3],同时存在对比度降低等问题[4]。基于物理模型的去雾算法对雾霾天气图像降质的原因进行分析并建立数学模型,据此复原出无雾图像,此类方法不易出现图像信息丢失的现象,复原图像更加接近真实图像[5]。已有多种基于多幅图像的去雾算法被提出[6-8],但是这类方法需要多幅图像处在单一场景下,所以在实际应用中效果欠佳且稳健性较差。文献[9]根据无雾图像比有雾图像有较大对比度这一先验条件来完成图像去雾处理,但该方法复原出的图像的局部区域会出现过饱和问题。文献[10]假设场景物体表面遮光部分与局部透射率不相关,并以此来估计透射率。但该方法处理浓雾时通常会出现失真现象。文献[11]通过假设大气耗散函数在某区域与最大值相近来完成图像去雾,但该方法在景深突变区域去雾能力较差。文献[12]提出了基于暗通道先验的图像去雾算法,该方法效率较低且在天空等明亮区域去雾后会出现失真。此外,研究人员还提出了暗通道去雾的改进算法。文献[13]引入了一种容差机制来解决复原图像天空失真的问题,但是该方法存在非明亮区域的误补偿以及过度补偿等问题。文献[14]提出了引导滤波来解决去雾图像边缘细节保持不够充分的问题,该方法虽然提高了去雾算法的效率,但去雾后图像在天空区域仍存在失真现象。此外,文献[15]根据天空区域的像素特点对天空区域进行识别提取,调整了天空区域的透射率,该方法耗时较长,且会出现天空区域误分割的情况。文献[16]定义了双透射率水下成像模型,在拓展暗通道算法应用场景的同时增强了算法的稳健性。文献[17]基于大气散射模型和卷积神经网络,提出了AOD-Net(all-in-one dehazing network)模型,通过轻量级的卷积神经网络直接生成清晰图像。文献[18]根据McMs-CNN(multi-channel multi-scale convolutional neural network)生成暗通道中估计场景的传输率,从而实现对单幅图像的去雾。此外,一种端到端的对抗生成网络算法也被提出用于单幅图像去雾[19],该方法也是直接复原图像而不考虑透射率的计算等问题。文献[20]提出了一种可训练的卷积神经网络用于对图像进行去雾,相较于手工预处理,该方法能取得更好的效果,同时在一定程度上缓解了常规多尺度方法遇到的问题,减少了复原图像的伪影现象。文献[21]基于卷积神经网络,通过比较器完成对透射率的估计,但对环境光值的估计存在偏差。此类基于深度学习的方法往往需要大量数据的支持,且难以在不同数据的泛化性上保证效果。此外,图像去雾算法已经应用于多个实际场景中[22-23]。
针对上述问题,本文提出一种基于引导滤波和自适应容差的图像去雾算法(IDAFT,image defogging algorithm based on guided filtering and adaptive tolerance)。引导滤波器是快速的边缘保持滤波器之一,可以使输出图像与引导图像的边缘保持一致,因此其可以用于代替软抠图来降低算法的时间复杂度。自适应容差能够根据图像天空区域的大小确定不同的容差参数,解决了引导滤波不能解决的天空区域去雾后的失真问题,修正该类区域的透射率值,得到更加准确的透射率,从而复原出更加优质的去雾图像。首先,通过求取不同尺寸邻域窗口的暗通道图和透射率图,对两幅透射率图进行线性拟合,得到相对准确的透射率图。然后,利用引导滤波,将带雾图像的灰度图作为引导图像,对透射率进一步细化。此外,为了解决复原图像的天空等区域的失真问题,提出一种自适应容差机制,对这些区域的透射率进行修正,使此类区域的透射率更加准确。最后,将图像从RGB 颜色空间转换到HSV颜色空间,对图像的亮度和对比度进行补偿,最终转换到RGB 颜色模型完成图像复原。
2 暗通道算法原理
2.1 大气散射模型
大气散射模型被广泛应用于图像去雾领域[12],简化后的大气散射模型可用于描述雾霾天气图像成因,具体如式(1)所示。
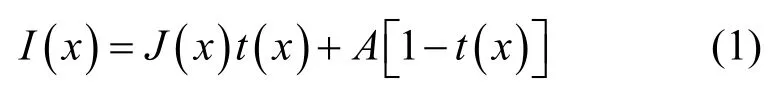
其中,I(x)和J(x)分别表示带雾图像和无雾图像;t(x)表示透射率;A表示大气光值;J(x)t(x)表示直接衰减项,可描述为光线在透射介质中的辐射和衰减;表示环境光成像,是大气散射现象的结果。基于该物理模型的图像去雾工作实际上是根据已知的带雾图像I(x)以及强力的先验知识或假设条件,得出A和t(x),进而复原出J(x)的过程。
2.2 暗通道算法原理
暗通道先验可描述为在绝大多数非天空局部区域内,某些像素总会有至少一个颜色通道具有很低的值。其数学表述为

其中,Jdark为暗通道,Ω(x)为以x像素为中心的方形邻域窗口,Jc为带雾图像J的R、G 和B 这3个颜色通道。由暗通道先验理论可知,在非天空区域Jdark一般很小,甚至趋近于0。
在假设A已知的情况下,对式(1)进行变换可得

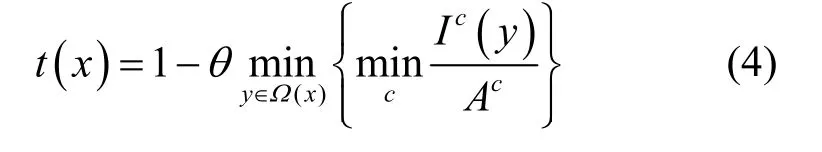
其中,θ取值范围为(0,1)。
将暗通道图中所有像素按亮度大小进行排序,选取亮度最大的前0.1%的像素点,在带雾图像中找到对应的像素点,将亮度最大的像素点取出,作为大气光值A。
根据式(1)复原出无雾图像。在图像去雾过程中,为了防止t(x)趋近于0 导致复原图像整体白场过度,为透射率设定一个下限值t0=0.1,最终得到复原图像为

2.3 暗通道算法存在的问题
暗通道算法中窗口大小的选取对结果有重要的影响,文献[12]对去雾图像进行了统一尺寸处理,然后选取固定的邻域窗口。在实际应用中,往往要处理尺寸各异的图像。一方面,如果选取的邻域窗口过大,那么窗口中出现暗通道的概率较大,但是在景深突变区,得到的暗通道和透射率图存在块效应,使复原图像存在白边缺陷。另一方面,如果选取的邻域窗口过小,则会因为较多区域不存在暗通道使复原图像出现色彩偏移。
此外,在暗通道算法中引入软抠图对透射率进行细化,虽然去雾图像白边缺陷得到了较好的解决,但是因为软抠图要涉及大型矩阵的计算,因此算法效率低下。
在天空等明亮区域中,像素点的3 个通道值都很大,不存在暗通道,此时根据式(3)计算像素点的真实透射率,且有,这就导致此类区域真实透射率大于计算所得透射率。因为透射率的错误估计,导致复原后的这些区域出现失真现象,如图2 所示。这严重影响了复原图像的视觉效果。此外,暗通道算法去雾后的复原图像还存在整体偏暗的问题。

图2 暗通道算法去雾后天空区域失真现象
3 IDAFT
本节提出一种基于引导滤波和自适应容差的图像去雾算法,首先利用双窗口拟合和引导滤波得到细化的透射率,然后利用自适应容差的方法修正天空等区域的透射率,最后基于HSV 颜色模型对图像亮度和对比度进行调整,得到最终的复原图像。
3.1 双窗口拟合优化透射率
在暗通道去雾算法中,计算暗通道图时邻域窗口大小的选取对图像去雾的效果有着重要影响。本文采用一种双窗口分别求取初始透射率,随后进行线性拟合的方法。首先分别选取15×15 和3×3 这2种尺寸大小的邻域窗口,根据式(2)分别求取2 种窗口对应的暗通道图。然后根据式(4)分别得到邻域窗口为15×15 和3×3 的透射率t15(x)和t3(x)。最后由式(6)对2 幅透射率图进行线性拟合得到透射率t(x)。
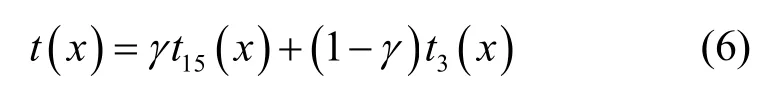
其中,γ为调节因子,本文设置γ=0.5。
未拟合和拟合后的透射率结果如图3 所示。

图3 不同情况下的透射率结果
IDAFT与暗通道先验算法求取大气光值A的方法类似,求取邻域窗口大小为15×15 的暗通道图,选取亮度最大的前0.1%的像素点,在带雾图像中找到对应的像素点。不同的是IDAFT 将这前0.1%的像素点的每个颜色通道的平均值作为大气光值A,取平均值是为了避免小面积白色非天空区域的影响,使取得的大气光值A能够更加趋近于真实值。
3.2 引导滤波细化透射率
虽然线性拟合得到的透射率相较于单一窗口的稳健性得到了提高,但是在边缘细节保持方面仍然显得不足,且算法复杂度仍然较高,为了解决此问题,IDAFT 采用引导滤波对透射率进行细化。
引导滤波假设引导图像I和输出图像q在以像素k为中心的方形窗口区域ωk内存在局部线性关系,即

由式(7)可知,q与I的梯度呈线性关系。在窗口ωk中代价函数可表示为

其中,ε为正则化参数,用于避免线性系数ak过大。ak和bk可以通过线性回归求解代价函数得到,即
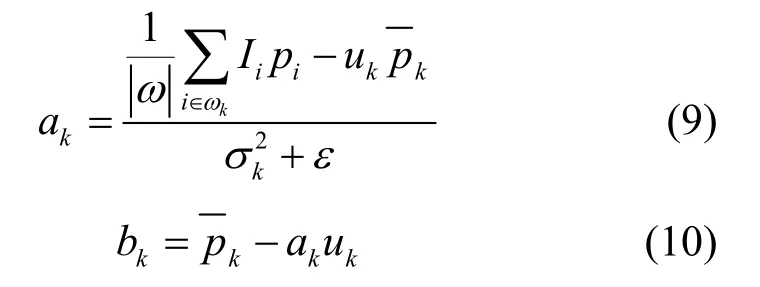
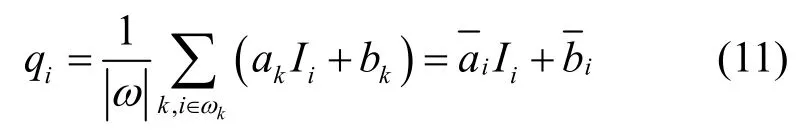
IDAFT 将带雾图像的灰度图作为引导滤波的引导图像,通过引导滤波得到细化后的图像透射率。图4 为引导滤波细化后的透射率结果。

图4 引导滤波细化后的透射率结果
3.3 针对天空区域的透射率补偿
为了解决图像去雾后天空区域出现失真的问题,在处理天空等明亮区域时,提出一种自适应容差机制,使容差参数能够根据图像包含天空等区域的大小来自适应地进行取值,这样使天空等明亮区域的透射率得到修正,而对于其他区域则保持原来的透射率。这种自适应调节机制既能够保证去雾后天空等明亮区域不会出现失真,也不会使大量非天空区域的透射率得到误补偿,从而能复原出质量更高的去雾图像。
在IDAFT 中,首先定义容差调节图为

其中,I c(x)为输入的带雾图像,α为调节因子,本文设置α=0.95。

其中,Stol为容差调节图中所有像素大于0 的元素集合,Snum为集合Stol中元素的总个数。
同时,定义容差参数为

其中,Ic(x)num表示输入图像中所有元素的个数。为容差参数设定上限,避免容差参数过大而导致非天空区域被误判为天空区域,从而减少非天空区域误补偿带来的影响。但是该上限值不宜过大,如果该值过大,则会导致大部分区域被判断为天空区域,使得到的透射率不准确,经过多次实验,当透射率取0.3 时,处理天空区域都能取得较好的效果,本文取该上限值为0.3。通过式(14),即可得到自适应的容差值K。图5 为不同场景下的带雾图像,图5(a)包含极少的天空区域,图5(b)则包含大量的天空区域。图6 为图5 中2 幅图像的容差参数K随调节因子α的变化曲线。

图5 不同场景下的带雾图像
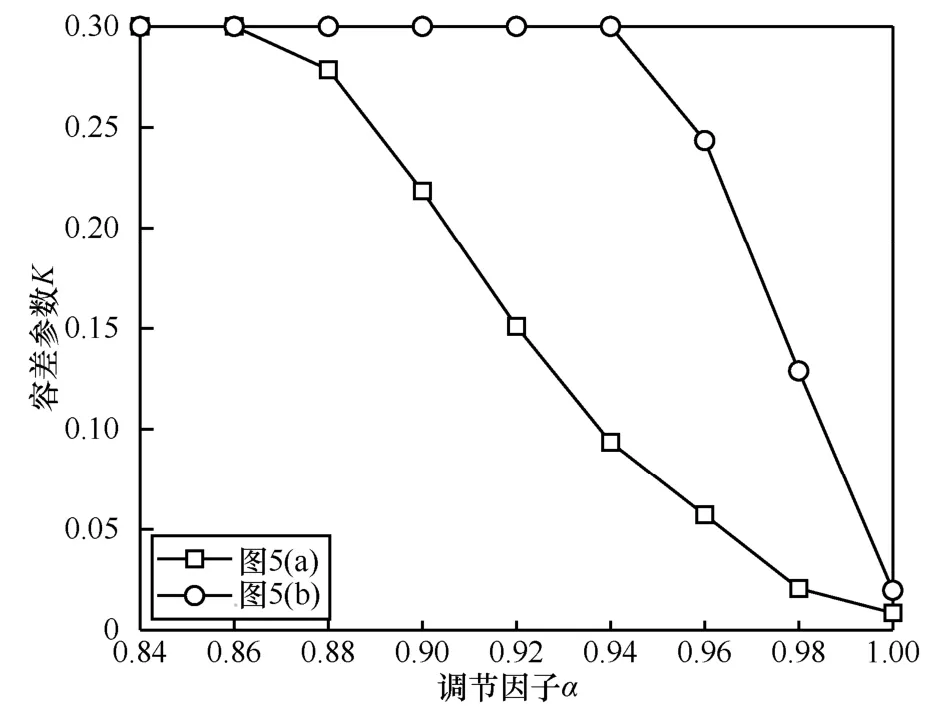
图6 容差参数K 随调节因子α 的变化曲线
引入容差机制为

根据自适应容差修正透射率,具体步骤如算法1 所示。
算法1自适应容差修正透射率
输入输入图像I,透射率t(x),大气光值A,容差调节参数α,容差参数阈值β
输出透射率t(x)


根据已经得到的大气光值、透射率图和已知的带雾图像,通过式(1)对图像进行去雾,即可得到初始复原图像。
3.4 颜色补偿
在雾霾天气下,受到空气中颗粒物对光的吸收和散射作用的影响,通常得到的图像像素点的亮度要比晴朗天气下的大。去雾后的初始复原图像整体偏暗,因此要对复原后的无雾图像进行色彩补偿。IDAFT 基于HSV 颜色模型对复原图像进行颜色补偿,流程如图7 所示。

图7 复原图像颜色补偿流程
首先,将得到的复原图像作为输入图像,将图像转换到HSV 颜色模型,对图像的S 和V 分量进行调整。然后,将调整后的图像转换到RGB颜色模型,输出图像即为颜色补偿后的最终复原图像。
4 实验结果与分析
为了验证IDAFT 的有效性,分别对若干幅雾霾天气图像进行实验,对去雾后的图像采用主观视觉评价和客观量化指标这2 种方式进行分析。实验的运行环境主要配置参数为64 位Windows10 操作系统,CPU 为Core i5-6300HQ@2.30 GHz,内存为8 GB。仿真实验的软件平台为Matlab R2018a。主要仿真参数如表1 所示。

表1 主要仿真参数
求取透射率调节参数θ是为了保留远处少部分的雾,这是因为雾的存在是人感知深度的一个基本因素[12]。θ的存在使去雾后的图像更加真实,θ越小,保留的雾就越多,通常取θ=0.95[12]。γ越大,拟合后的图像与大窗口得到的透射率图越相似;反之,与小窗口得到的透射率图越相似。γ在[0.4,0.6]范围时拟合效果较好,本文取γ=0.5。经过多次实验可知,当α在[0.93,0.96]范围时有较好的效果,本文取α=0.95。γ取值对去雾效果的影响与处理图像的尺寸有关,本文取r=60像素。ε是一个很小的数[14],ε在(0,0.01]范围时都能取得较好的实验结果,本文取ε=0.001。
4.1 主观视觉评价
分别选取不含天空区域、含较少天空区域、含较多天空区域和含大量天空区域的带雾图像进行实验,不同场景下各算法去雾效果比较如图8 所示。图8 中前三行的图像均来自He[12]主页,图8(d1)~图8(d6)和图9 来自Flickr.com 和百度图片搜索引擎,为包含大量天空区域的图像。通过仿真实验,分别对每幅图像使用文献[12]算法、文献[14]算法、文献[21]算法、文献[24]算法以及IDAFT 进行去雾处理。
通过将去雾图像与带雾图像进行比较可以看出,5 种算法都有一定的去雾效果。在不含天空区域、含较少天空区域和含较多天空区域的场景下,5 种算法都能够对图像完成有效的去雾,IDAFT 在景深突变区过渡更加自然,色彩还原度更高,在远景处能取得更好的效果。在包含较多天空区域的场景下,文献[12]算法和文献[14]算法在天空区域去雾后出现了失真现象,这种情况在包含大量天空区域的图像中尤其明显,而文献[21]算法、文献[24]算法和IDAFT 在这些区域没有出现失真现象,能够很好地对图像进行去雾,而且从图8(d)可以看出,IDAFT 复原图像整体的色彩还原度更高。此外,由图9 可以直观地看出,IDAFT 在对天空等区域的处理也能得到很好的处理效果。

图8 不同场景下各算法去雾效果比较

图9 包含大范围天空区域场景下各算法去雾效果比较
4.2 量化指标比较
为了更加全面地测试各算法的去雾效果,选取包括平均梯度、可见边的规范化梯度均值[25]、信息熵和算法运行时间作为评价指标对算法进行量化的比较。
平均梯度反映了图像的细节,平均梯度越大,表明图像的轮廓信息越清晰。
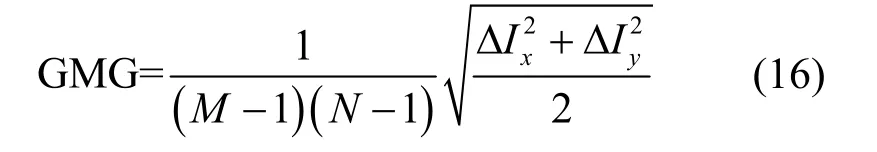
其中,M和N分别为图像的宽和高,ΔIx和ΔIy分别为水平方向的梯度和垂直方向的梯度。
可见边的规范化梯度均值反映了去雾后图像边缘对比度的变化,可见边的规范化梯度均值越大,表明图像的去雾效果越好。

其中,nr表示去雾后图像的可见边数目[25],Pi表示可见边上的像素点,ϑ r表示去雾图像所有可见边的集合,zi表示可见边的相关系数。
信息熵反映了图像的信息量,信息熵越大,表明图像包含的信息越多,去雾效果越好。
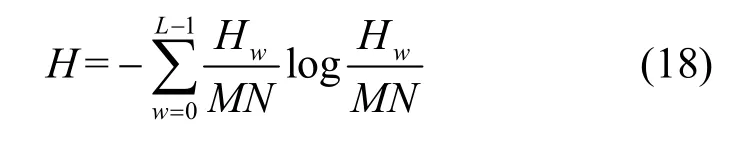
其中,M和N分别表示图像的宽和高,L表示图像的最高灰度级,Hw表示灰度级为w的像素的个数。
算法运行时间反映了算法运行所耗时间,时间越少,表明算法的效率越高,算法执行代价越低。5 种算法对不同图像的去雾能力比较如表2 所示。
从表2 中可以看出,IDAFT 的运行时间与文献[24]算法时间相近,远低于文献[12]算法,略高于文献[14]算法,且有较高的效率。这是因为文献[12]算法利用软抠图的方式优化透射率,而软抠图涉及大型拉普拉斯矩阵的运算,该矩阵的大小为去雾图像大小的平方,因此算法效率低;文献[14]算法通过引导滤波优化透射率,算法效率较高;本文同样运用引导滤波,并且对天空等区域的透射率进行了再一次细化,同时对图像色彩进行补偿,因此IDAFT 运行时间要略大于文献[14]算法。文献[21]算法因为要进行模型训练,此过程需要大量时间,远高于其他4 种算法,因此在表2 中没有记录。文献[12]算法、文献[14]算法、文献[24]算法及IDAFT运行时间随图像尺寸变化曲线如图10 所示。
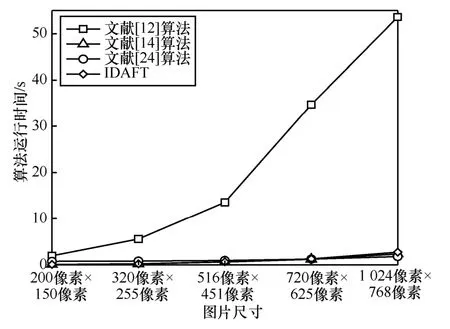
图10 4 种算法运行时间随图像尺寸变化曲线
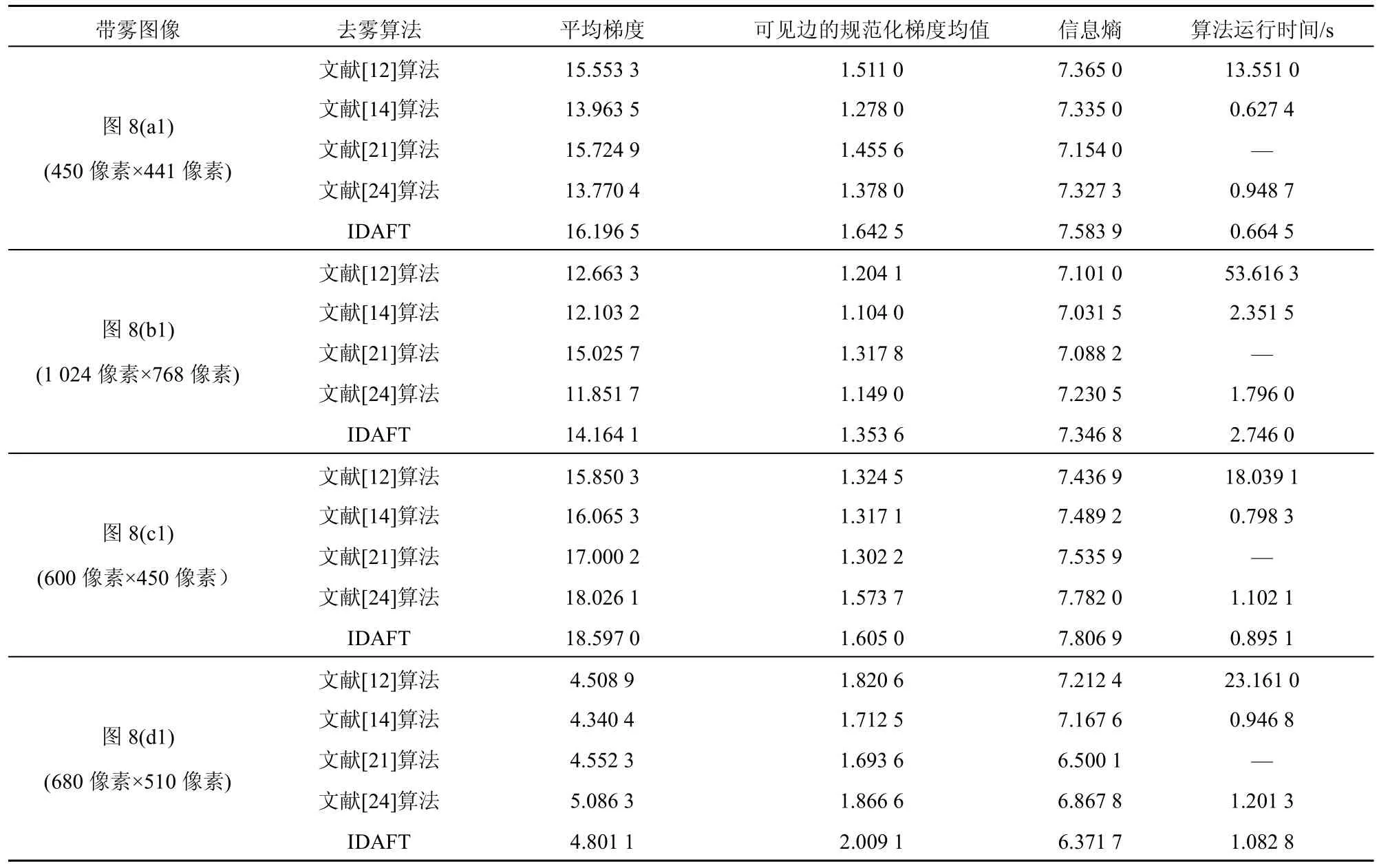
表2 5 种算法对不同图像的去雾能力比较
同时从表2 也可以看出,对于图8(a1)~图8(a6)、图8(b1)~图8(b6)和图8(c1)~图8(c6),IDAFT 在除算法运行时间外的其他各个评价指标相较于其他4种算法都有更好的表现。图8(d1)~图8(d6)中,IDAFT 的平均梯度和可见边的规范化梯度均值整体优于其他4 种算法。在信息熵方面,对于包含较多天空区域的图8(d1)~图8(d6),IDAFT 得到的图像信息熵要低于其他4 种算法,这与其他4 种算法在天空去雾后出现失真后引入了噪声有关,同时这也说明IDAFT 在针对天空区域透射率的修正是更加有效的。
为了更全面地对算法进行比较,从Flickr.com和百度等图片搜索引擎中获取包含较多天空区域的带雾图像,并与He 主页带雾图像构成图像集。然后将该图像集的图像根据包含天空区域面积的大小再均分(包含图片数量相等)为3 个图像集:不包含或者包含极少天空的图像组成图像集1,包含少量天空区域的图像组成图像集2,包含大范围天空区域的图像组成图像集3。
对3 个图像集的所有图像分别用5 种算法进行去雾处理,得到平均梯度、可见边的规范化梯度均值、信息熵这3 项量化指标各自的平均值,分别如图11~图13 所示。
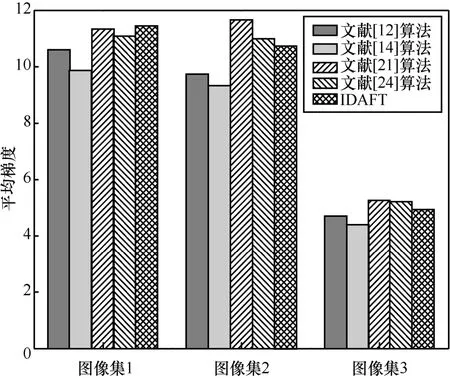
图11 平均梯度指标比较
从平均梯度指标来看,IDAFT 在图像集1 的表现优于其他4 种算法,在图像集2 和图像集3 的表现与文献[24]算法相近,低于文献[21]算法,优于其他2 种算法。从可见边的规范化梯度均值指标来看,IDAFT 除了在图像集3 的表现略差于文献[24]算法之外,相较于其他算法均有更好的表现。从信息熵指标来看,IDAFT 在图像集1 和图像集2 的整体表现优于其他4 种算法,在图像集3 得到的结果低于其他4 种算法,这与其他算法在该类区域去雾后失真引入噪声等因素有关。因此,通过实验可以证明,IDAFT 是可行且有效的。
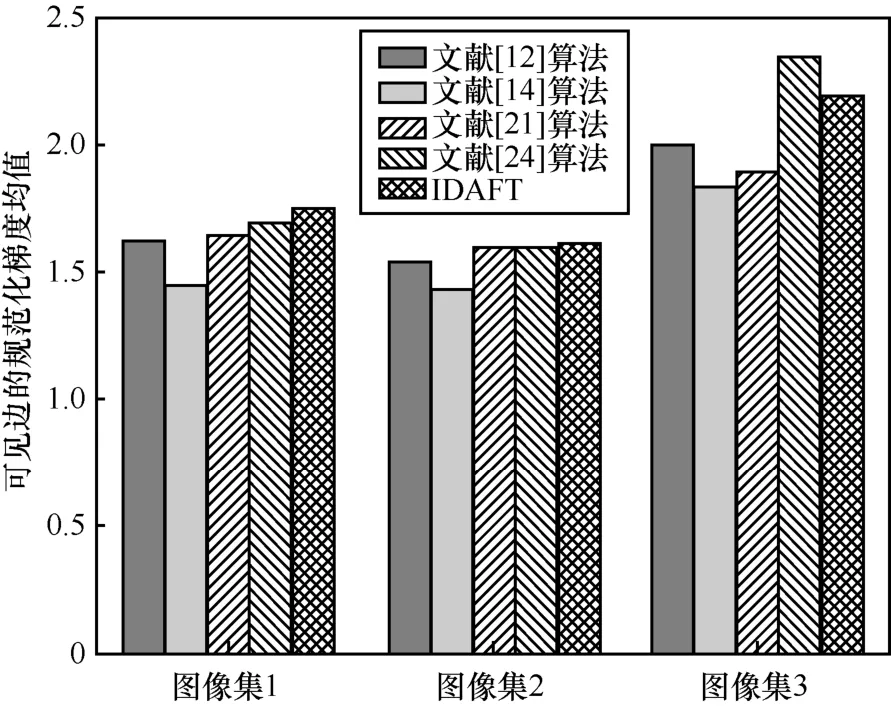
图12 可见边的规范化梯度均值指标比较

图13 信息熵指标比较
5 结束语
本文针对暗通道算法图像去雾后存在天空区域失真等问题,提出一种基于引导滤波和自适应容差机制的图像去雾算法。首先,分别计算不同尺寸窗口暗通道和透射率图,对两幅透射率图进行线性拟合,得到了更加精确的透射率。然后,将灰度图作为引导图像对透射率进行引导滤波,在解决景深突变区块效应的同时,提高了图像去雾算法的效率。特别地,通过自适应容差机制,可以对天空区域的透射率进行修正,解决了此类区域去雾后出现的失真问题。最后,基于HSV 颜色模型对去雾图像进行颜色补偿。仿真实验结果表明,IDAFT 得到的复原图像亮度更高,色彩更加鲜艳,图像的整体视觉效果更佳,对于天空和非天空区域都能够取得较好的去雾效果,在平均梯度、可见边的规范化梯度均值、信息熵量化指标也有很好的表现。
