特征算子谱表示与特征展开的研究
2020-06-06王宏禹邱天爽
王宏禹,邱天爽
(大连理工大学电子信息与电气工程学部,辽宁 大连 116024)
1 引言
在信号分析与处理研究及应用中,特征算子的谱表示与特征展开(特征分解)具有重要意义。特征算子谱表示过去主要在量子力学中用于研究原子谱表示,随着量子通信技术的迅速发展,量子信号处理理论与应用也将得到快速发展。此外,特征算子的特征展开可用于大数据处理。因此,特征算子谱表示与特征展开的研究是很有意义的。近年来,作者针对特征算子谱表示与特征展开存在的问题发表了3 篇论文,分别是研究特征微分方程的格林函数、特征谱表示及长球面波函数[1-3],虽然取得了新进展,但仍存在一些理论不清的问题。为此,本文又对其进行了深入研究,得出以下结论。1) 特征微分方程的格林函数g(x,ξ)非常重要,基于对它的研究分别给出厄尔密特微分算子谱表示与厄尔密特积分算子展开式,并给出它们为互逆的关系式。2) 厄尔密特微分算子谱表示式是无穷维的,它比诺伊曼研究法简单清楚,具有优越性。但是,斯−刘(S-L,Sturm-Louville)特征微分方程都是有限区间的,不能将其用于谱表示的具体实现中。3) 厄尔密特积分算子只能用于特征展开,不能用于谱表示,改正了文献[2]中可用于谱表示研究的不正确论述。4) 利用矩阵理论中椭球主轴研究成果及长球面波函数[4]二重正交性成果,对特征积分方程的长球面波函数的数学物理意义给出了清楚的解释。
2 特征算子谱表示
2.1 特征微分方程
在信号处理中,信号展开基函数所用的正交特殊函数均可用如式(1)所示微分算子L的特征微分方程(斯−刘微分方程)[5-6]得到,如式(2)所示。
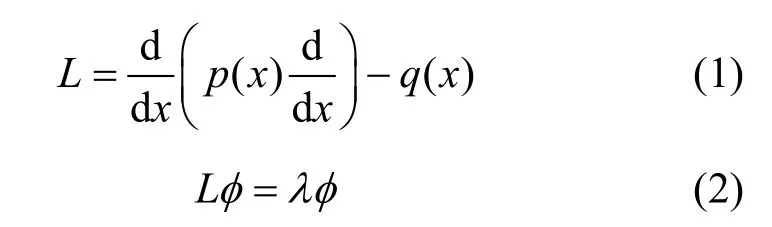
其中,p(x)和q(x)在所论区间都是连续的,且p(x) > 0;λ为特征值,由无穷个λi组成,当q(x) >0时,λi都不是负数;与λi对应的φi称为特征函数,φi是正交的;p(x)和q(x)的所论区间为[a,b],即
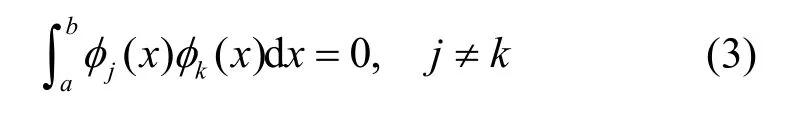
将特征值按递增顺序排列,可得到一个无限序列λ1<λ2< …<λi<…,这个序列称为特征微分方程的谱。在满足适当边界条件下,对于2 个函数f(x)与g(x),式(1)所示微分算子L满足如式(4)所示的内积关系。
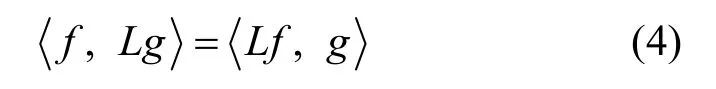
因此,式(1)所示的微分算子L是厄尔密特的。
2.2 特征微分方程的格林函数
任意函数f(x)可表示为正交的归一化特征函数φk(x)的无限展开式,如式(5)所示。
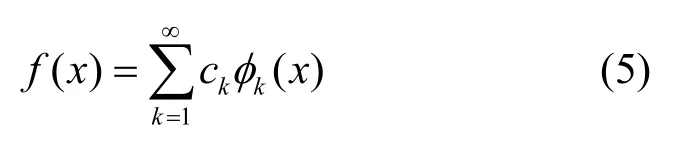
其中,ck为展开系数。若φk(x)是正交归一化的,即
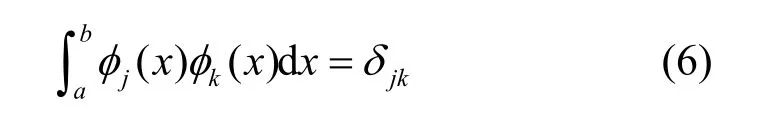
则由式(6)可得展开系数ck为
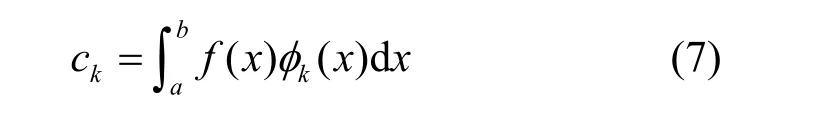
式(5)所示的f(x)可以表示为微分算子L的非齐次微分方程的解,如式(8)所示。

根据线性系统理论,u(x) 为系统的输入,f(x)为系统的输出。根据式(2)、式(4)及式(8),将g=φk代入式(4)中,得
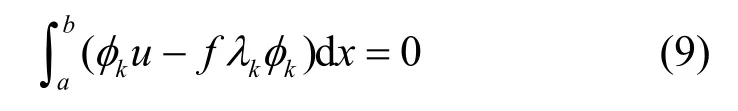
利用式(9)可得式(7)中展开系数ck的表示式,为
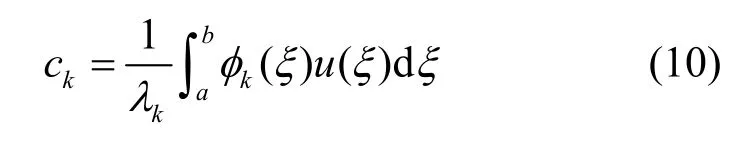
将式(10)中ck代入式(5),可得
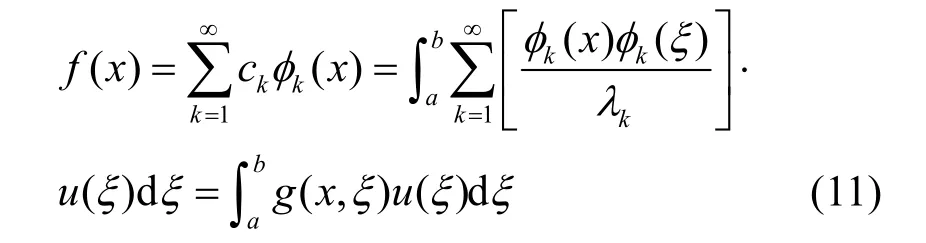
其中,
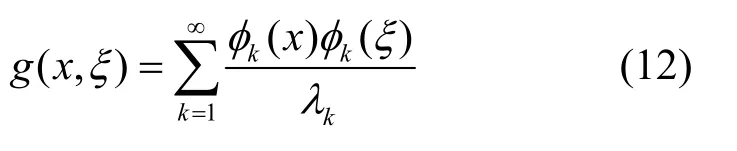
由于式(11)为输入u(ξ)与输出f(x)的积分形式,因此g(x,ξ)是与时变系数微分算子L对应的线性时变系统的格林函数[7-9]。当输入u(x)=δ(ξ−x0)时,得到输出f(x)如式(13)所示。
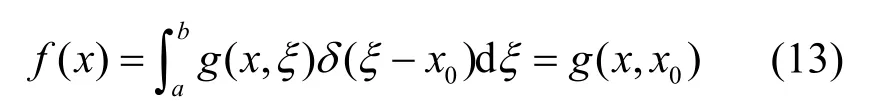
即对于线性时变系统,格林函数g(x,x0)为在x0处施加单位脉冲而在x处所得的输出f(x)。由式(8)与式(13)可得
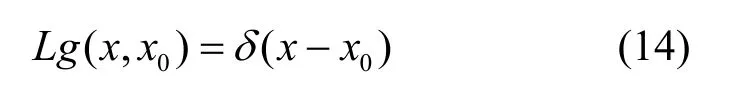
式(14)表明,厄尔密特微分算子L是其特征微分方程格林函数g(x,x0)的逆算子[10]。
2.3 特征微分算子与格林函数的关系
根据2.2 节的研究,厄尔密特微分算子L与其格林函数g(x,ξ)的关系为Lg(x,ξ)=δ(x−ξ),当ξ=x时,有

而当ξ≠x时,δ(x−ξ)=0,式(15)关系不存在。将式(6)归一化特征函数φi(x) (i=1,2,…) 的形式表示成离散和形式,即

根据式(15),当δ(x−ξ)在ξ=x时,得
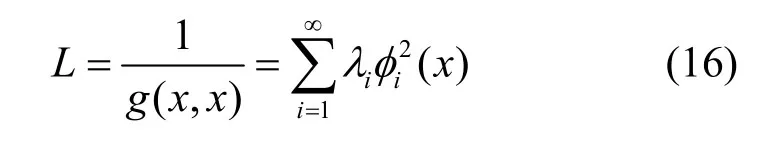
式(16)就是厄尔密特微分算子L谱表示无穷维离散和的形式。
2.4 斯−刘问题
对于2.1 节的斯−刘特征微分方程,需要加上边界条件进行研究,这种研究称为斯−刘问题。对2.1节斯−刘特征微分方程中的函数p(x)与q(x)做如下假设。设函数p(x)与q(x)及其导数在闭区间[a,b]上均连续,当a
为了后面研究的需要,本文采用加权斯−刘微分方程的边值情况说明,如表1 所示。表1 中ρ(x)=1的情况即为通常的斯−刘微分方程,有调和微分方程、勒让德微分方程及连带勒让德微分方程。
式(16)厄尔密特微分算子L谱表示没有考虑上述边界值情况的研究结果,因此,不能将表1 中闭区间研究的斯−刘问题λn与φn用于其具体实现。但式(16)的L谱表示在理论上是正确的,因此可以作为一类厄尔密特微分算子L的一种无穷维离散和谱表示。为了说明方便,将式(16)及归一化特征函数φn(x)描述如下。
厄尔密特算子L的无穷维离散和表示式为
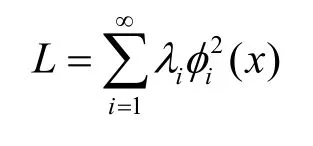
归一化特征函数离散表示式为
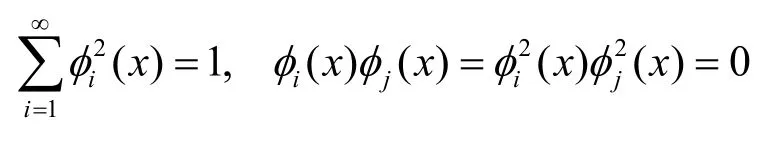
要将式(16)中L表示成积分形式,首先介绍取值的函数,其定义为
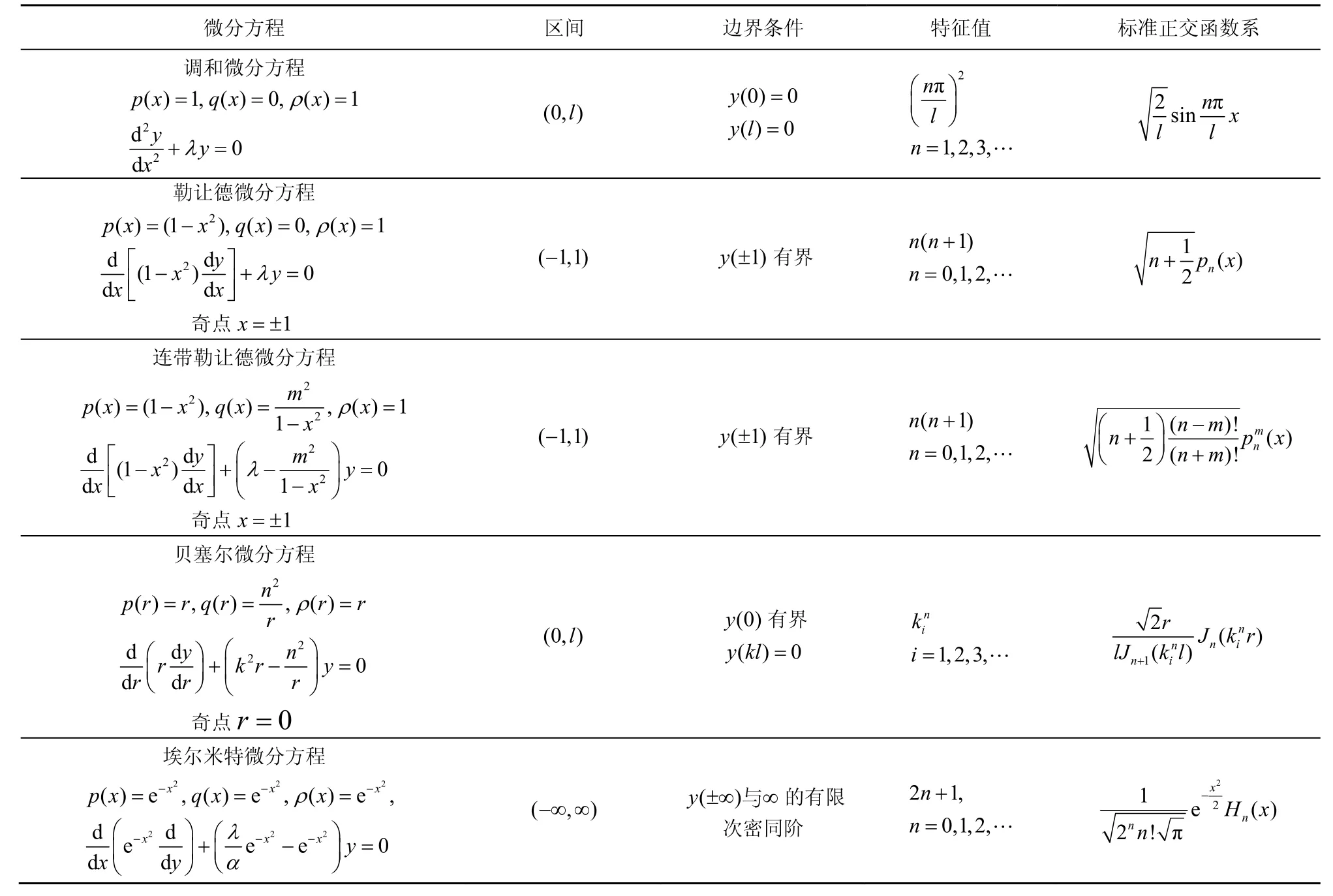
表1 加权斯−刘微分方程边值情况
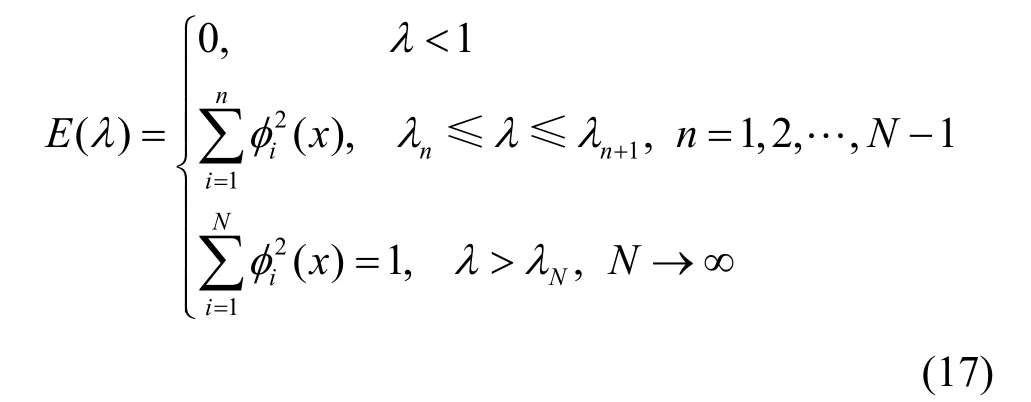
式(17)中的E(λ)示意如图1 所示。
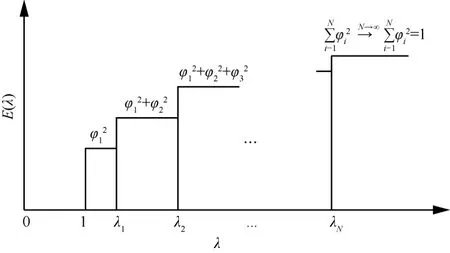
图1 E (λ)示意
由式(17)可得
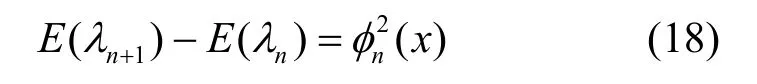
当各λi(i=1,2,…) 无限接近时,由勒贝格积分可得
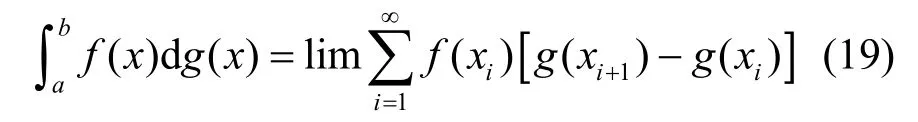
其中,lim 表示趋向非常小的划分区间[i+1,i],i=1,2,…。
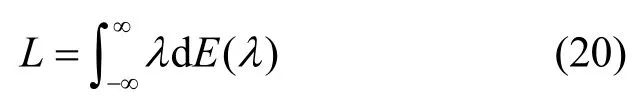
上述研究结果与诺依曼的厄尔密特算子连续谱的表示式相同,并且与之相比数学物理意义更加清晰,具有明显的优越性。
为了进一步表明式(16)谱表示理论的正确性,下面用2 个正弦谱表示理论来说明。
1) 确定性非周期信号x(t)的傅里叶积分。对x(t)的傅里叶级数展开,x(t)必须在闭区间[ −l,l]是周期的,但实际应用中的许多信号是非周期的,因此需要解决这个困难问题。有学者给出了回避在[ −l,l]闭区间周期性的要求,将l扩展成l→∞来解决,得出非周期傅里叶积分。
2) 平稳随机信号x(t)的谱分解。采用随机振幅简谐振动叠加法可得平稳随机信号x(t)的谱分解,表明x(t)是由无限个频率由小到大连续变化的随机幅度简谐振动叠加而成的[2]。
2.5 加权的斯−刘微分方程
通常的斯−刘微分方程因存在边界条件问题,只能用于有限区间研究,为此,有学者给出了加权斯−刘微分方程来解决,即

表1 中的埃尔米特微分方程属于加权的斯−刘微分方程,它的存在区间是(−∞,∞)。因此,可用于研究谱表示算子的实现。这充分表明本文研究的谱算子理论正确清晰且可实现,具有优越性。
3 特征积分算子展开
3.1 积分算子方程与特征积分方程
在数学中,积分算子方程K定义为
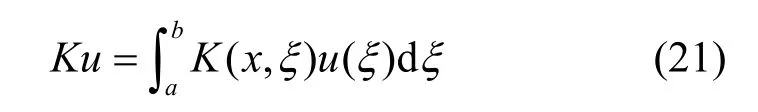
其中,K(x,ξ)为核函数。若K(x,ξ)选择如式(12)所示的特征微分方程的格林函数g(x,ξ),则,,此外,还应考虑。当输入u i(ξ)=φ i(ξ)时,由式(21)得
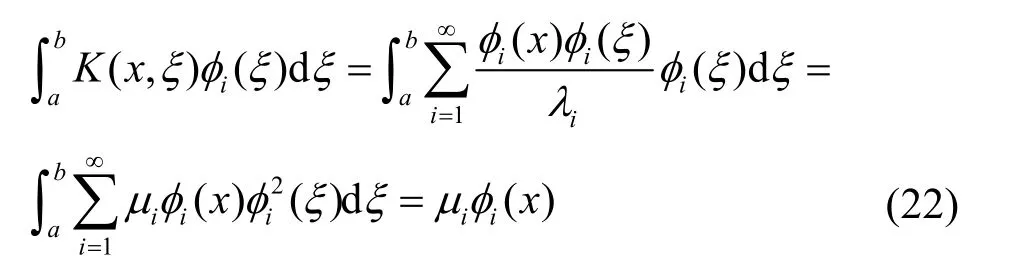
式(22)就是特征积分方程,该特征积分方程具有以下性质。
1) 特征积分方程核函数K(x,ξ)=g(x,ξ)是厄尔密特的。
2) 特征函数φi(x)是正交归一化的,即。
3) 特征值μi是实数,并满足1>μ1≥μ2≥ …。这是因为,其中,λi是递增序。
当积分算子K方程的核函数K(x,ξ)=g(x,ξ)与输入u=δ(x−ξ)时,得
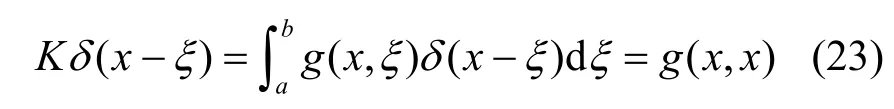
由于x≠ξ时,δ(x−ξ)=0,因此,当x=ξ时,可将δ(x−ξ)视为 1。实际上,当x=ξ时,δ(x−ξ)=∞,而,于是,积分算子K为
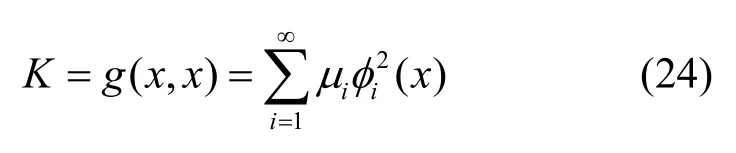
积分算子K中特征值μi是递减序,不能用于研究特征值递增序的厄尔密特微分算子L谱表示,而只能用于积分算子特征分解或特征展开的研究。
3.2 椭球的主轴
要对信号的特征算子分解的物理与几何意义有清楚的了解,有必要介绍数学矩阵特征理论中椭球的主轴。
n维球心位于原点的椭球方程为
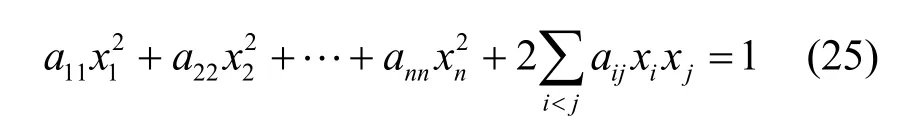
若i>j,α ij=αji,令矩阵A=(αij),i,j=1,2,…,n,A是对称矩阵,则式(25)可表示为
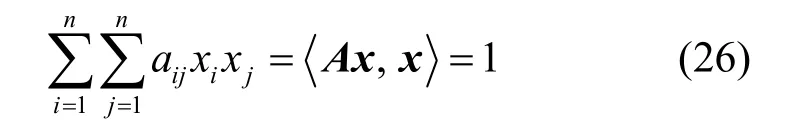
椭球的主轴是从原点起始并垂直于球上点x的矢量,对n=2 即椭圆情况,如图2 所示,它有2 个独立的主轴,且它们是相互正交的。
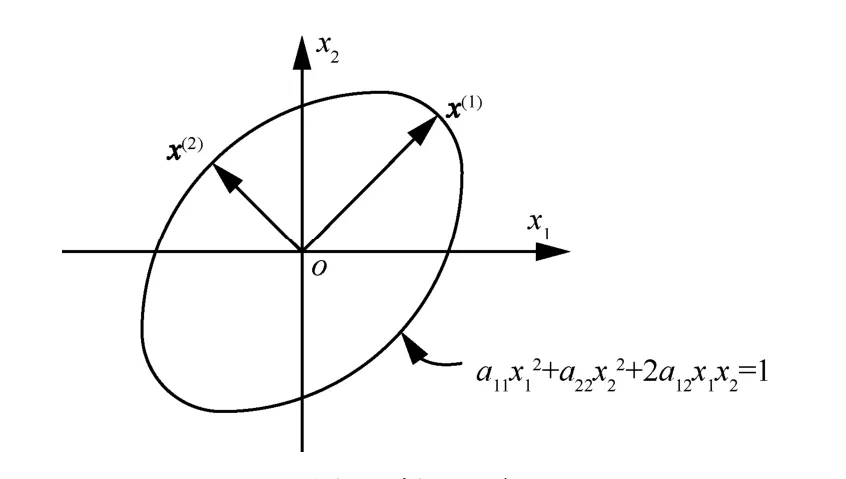
图2 椭圆示意
当n=2 时,椭圆的主轴情况可推广成n>2 时的一般情况。椭球的主轴有一重要性质,即它们是实对称矩阵A的特征矢量,对此研究描述如下。
若n维曲面Φ(x1,x2,…,xn)=C,C为常数,则有
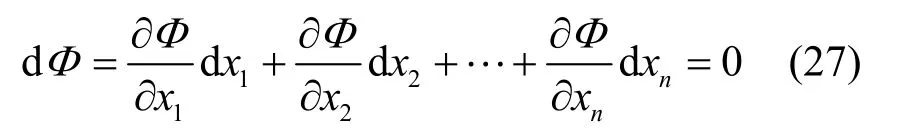
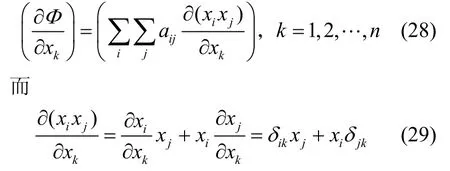
将式(29)代入式(28),并考虑aik=aki,有
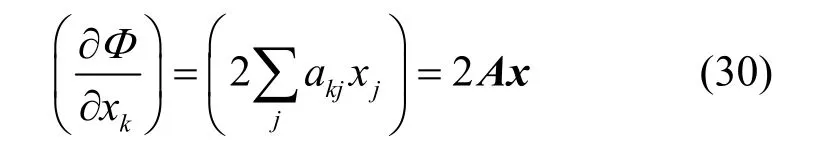
式(30)是与椭球Φ=1在点x正交的矢量,若x是椭球的主轴,则其也是在该点的正交矢量。因此,它们之间的关系为

其中,μ为实数。式(31)为矩阵A的特征方程,x为其一个特征矢量。由此证明了椭球的主轴x是矩阵A的一个特征矢量。式(31) 有内积关系,因此,椭球主轴长度是μ,主轴坐标位置是。由于必须是正数,因此特征值μ也必须是正数。
上述研究的是n维实对称特征矩阵一主轴情况,可以将其推广成无穷维实对称核函数特征积分方程情况,从而可以得出它们的各特征值与一个无穷维椭球的各主轴相对应。
3.3 长球面波函数
1) 信号分析与处理中的不确定性原理简介
信号分析与处理中的不确定性原理是信号的时宽D与频带宽B不能同时小于一最小值Cmin,即BD≥Cmin。另外,为了有效利用信号,其时宽与频带宽不能同时是无限的。这样,需要解决信号频带Ω限于与时间限于信号是什么的问题,这就是所需要研究的长球面波函数信号。
2) 长球面波函数特征积分方程表示式
对于σ−BL(σ带宽信号表示)信号φ(t)用带通Ω≥σ的理想滤波器K(t,x)进行无失真滤波,并用的矩形波时间函数进行时间范围截取,这种情况可表示为
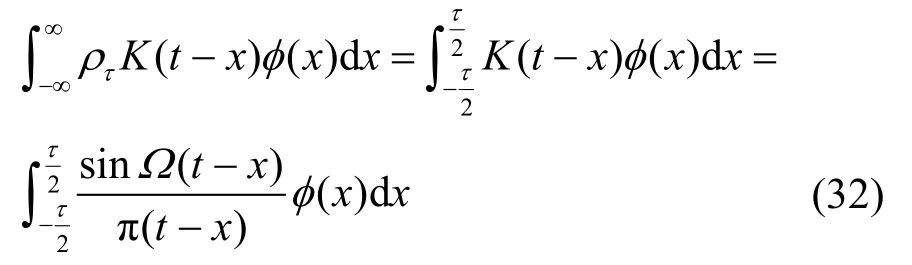
根据特征积分方程理论,核函数K(t,x)的作用是改变原来特征函数φ(x)的“长度”,而“长度”是用特征值μ表述的。这样,可将式(32)表示为
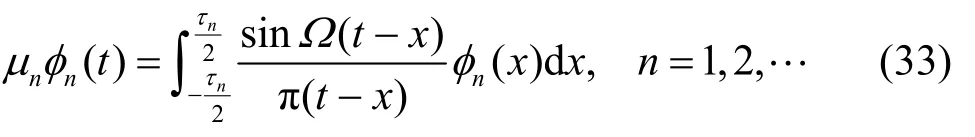
式(33)就是长球面波函数的特征积分方程表示式。
3) 长球面波函数特征积分方程的性质
①积分方程中特征值μn不是任意的,只是对某些特定值该积分方程才有解,μn是正实数,并且是递减序的,有
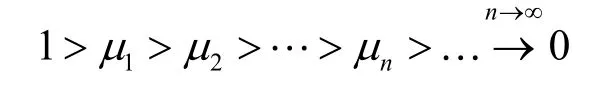
②对每一个μn,对应的特征函数φn(t)在(−∞,∞)区间内构成实正交归一化函数集,即
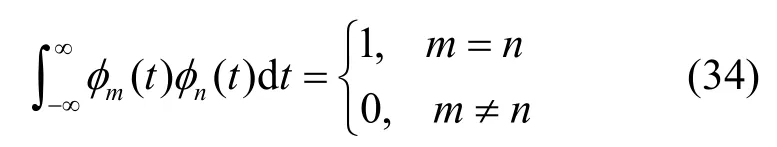
其中,m,n=1,2,…。
③任意一个带限函数(σ−BL)信号f(t)都可展成φn(t)的级数形式,即
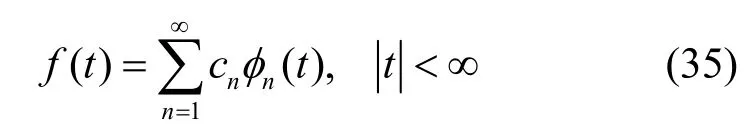
其中,
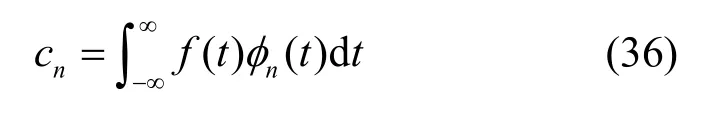
上述3 个性质是一般特征积分方程都具有的,对于长球面波函数特征积分方程,还有一重要的双重正交性质,即它在也是正交的,有
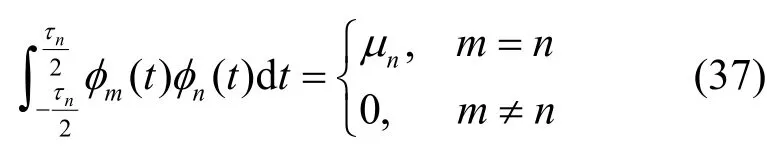
其中,m,n=1,2,…。
式(37)证明如下。对式(33)两端乘以φm(t),从−∞到∞积分,则式(33)左端有
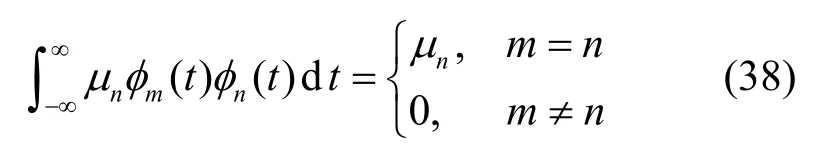
其中,m,n=1,2,…。而式(33)右端改变积分先后顺序后,有
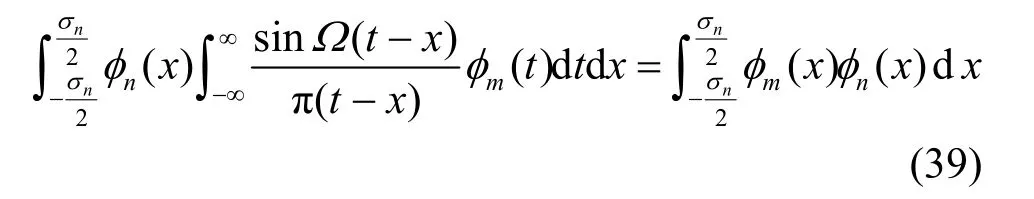
于是,由式(38)与式(39)可得
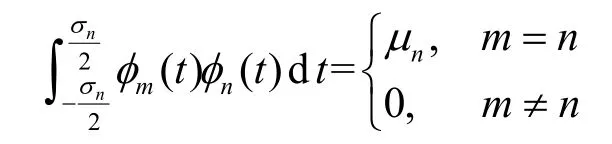
即为证明的式(33)。
4) 长球面波函数物理与几何意义
根据长球面波函数的双重正交性质,由式(33)可得
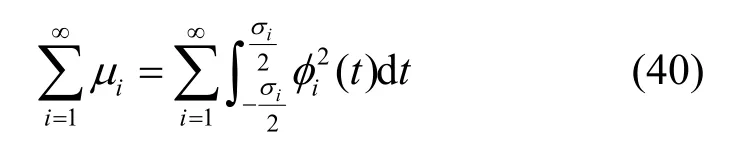
式(40)中等号右边的离散和表示式可表示为特征函数φi(t)归一集的表示式,即
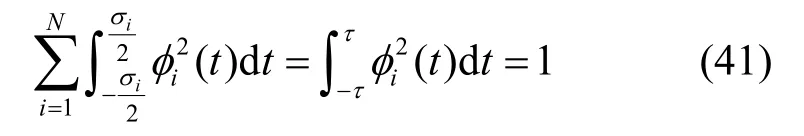
根据信号正交投影几何理论,式(40)与式(41)可表示为

根据3.2 节可知,式(42)可用来说明椭球主轴理论的几何与物理意义。显然,μi是椭球上的长度,而是μi在坐标上的坐标位置。为了方便和清楚地表示,给出i=1,2椭圆情况时的示意如图3 所示,椭圆的最长主轴为最大特征值。
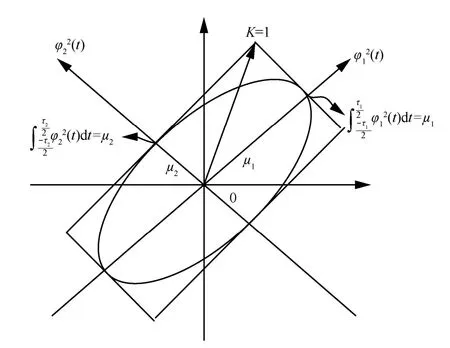
图3 长球面波函数对应的椭圆情况示意
4 分析与讨论
4.1 特征微分算子与谱表示
特征微分方程的格林函数g(x,ξ)=在本文研究中有重要意义。当线性时变系统输入为δ(x−ξ)时,g(x,ξ)为输出,与特征微分算子L的关系为
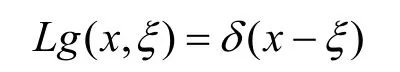
当x=ξ时,有Lg(x,x)=1,,。
4.2 厄尔密特积分因子与特征展开
对于特征积分方程,当其核函数K(x,ξ)选择为特征微分方程的格林函数时,即K(x,ξ)=g(x,ξ)=,特征值,得特征积分方程为

对特征积分算子方程,若输入为δ(x−ξ),有
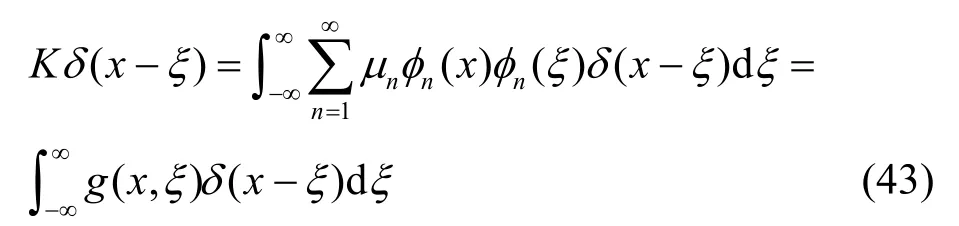
当x=ξ时,δ(x−ξ)=1,由式(43)得
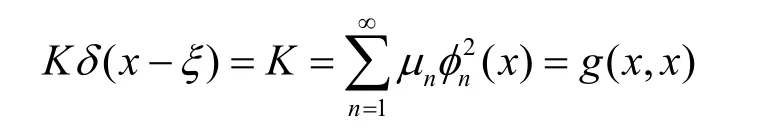
其中,1>μ1>μ2> …>μn>…为递减序,于是,厄尔密特积分算子K可用于特征展开或特征分解,而不能用于研究特征谱表示。
4.3 L 与K 的关系
特征积分算子方程的核函数K(x,ξ)为微分算子Lg(x,ξ)=δ(x−ξ)时的格林函数,因此,当x=ξ时,得L与K的关系为
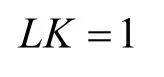
其中,有
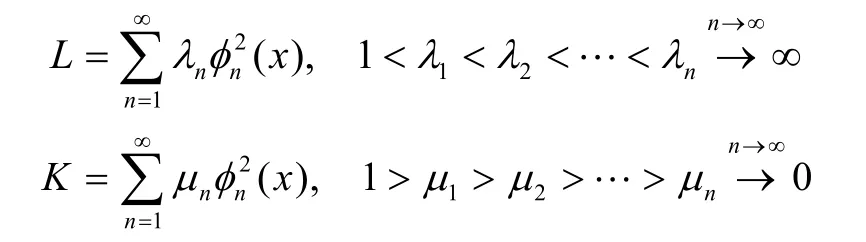
由此可得如下结论。
1)λn与μn(n=1,2,…) 的关系为,。
2)L与K的特征值序列可构成如下的一个联合排序LK=1表明L与K互为逆算子关系,即
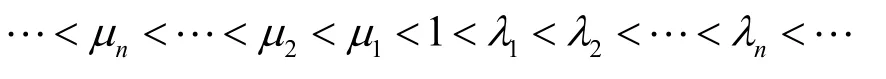
μn与λn(n=1,2,…) 序列分界点在1 处。
4.4 椭球主轴与长球面波函数
2) 长球面波函数在一般数学文献中很少见到其研究成果,但在信号分析与处理文献中却有不少研究成果,因为它是由研究信号最优波形设计得出的,并应用于信号展开、最佳窗函数设计等中,至今仍存在理论不清之处,从而影响对其函数名称的清楚理解。本文根据长球面波函数特征积分方程中双重正交性质,即,将其补充到上述椭球主轴研究中,可以得出长球面波函数φn(x)几何与物理意义如下,几何示意如图3 所示。
①特征算子K中(n=1,2,…)是椭球坐标系中的坐标轴。
② 特征值μn是与其对应坐标轴上的椭球主轴长度,最大特征值为椭球最长主轴。
③μn所在坐标轴上的坐标值(坐标位置)为。
5 结束语
针对特征算子谱表示与特征展开研究中尚存在的理论不清问题,本文进行了深入研究,得到一些有意义的理论结果。本文首先给出了特征微分方程格林函数与厄尔密特微分算子及厄尔密特积分算子的关系式,表明了厄尔密特微分算子与厄尔密特积分算子的互逆关系,并给出了厄尔密特微分算子的谱表示,指出了有限区间斯−刘特征方程不能用于无穷维谱表示的原因;然后给出了厄尔密特积分算子的特征展开,具有理论上一般性意义,并对特征积分方程的长球面波函数的数学物理意义给出了清楚解释。本文的研究结果对于进一步深化关于特征算子谱表示与特征展开理论研究具有重要意义。
