基于无意调相特性的雷达辐射源个体识别

秦鑫，黄洁，王建涛，陈世文

（信息工程大学数据与目标工程学院，河南 郑州 450001）

1 引言

特定辐射源个体识别（SEI,specific emitter identification）是指通过对接收机截获的辐射源信号进行测量、分析，并根据已有的先验信息辨识个体的过程，是电子侦察的重要环节[1]。早期雷达辐射源个体识别主要通过载频、脉宽和脉冲重复周期等常规参数进行模板匹配实现。随着雷达技术水平的提高，新体制雷达不断出现，电磁环境日益密集复杂，传统基于外部特征参数测量的方法已经难以满足快速、准确区分辐射源个体的需求[2]。雷达辐射源个体的差异是由发射机内部器件固有的非理想特性导致的，这种非理想特性对信号的影响是细微的，称为无意调制（UMOP,unintentional modulation on pulse）。在传统方法失去作用的情形下，通过分析信号的UMOP 特性以实现特定辐射源识别已成为一个重要的研究方向。

目前，已有文献的研究主要集中于从时域[3-7]、频域[8-9]、变换域[10-11]等角度分析提取能够反映UMOP 的独立稳定可测特征。文献[5]从实际工程应用出发，在中、高信噪比条件下，通过直接估计脉内瞬时相位的手段提取无意调相（UPMOP,unintentional phase modulation on pulse）特征曲线作为辐射源个体特征，采用最近邻（NN,nearest neighbor）分类算法实现个体识别，取得了较好的识别效果。但该方法仍然存在以下不足。1) 利用时域加窗平滑对UPMOP 特征曲线进行降噪处理，受噪声影响较大，当信噪比相对较低时，降噪处理后UPMOP 特征曲线仍弯折抖动明显，不利于分类器学习；2) 分类算法采用基于欧氏距离的最近邻算法，但UPMOP 特征曲线是典型的时间序列，其所有信息都包含在不同时刻的变化中，数据在时间维度上的关联性非常重要，传统基于欧氏距离的最近邻分类算法无法很好地解决这一问题。

为解决现有基于UPMOP 特性实现雷达辐射源个体识别方法的欠缺，本文提出一种基于UPMOP特性分析和长短时记忆加全卷积网络（LSTM-FCN,long short term memory fully convolutional network）的雷达辐射源个体识别算法。该算法利用贝塞尔曲线[12]光滑的特点，对UPMOP 进行贝塞尔拟合以获得平滑序列，引入深度学习技术，构建LSTM-FCN[13]模型自动提取UPMOP 序列特征进行分类识别。实验表明，本文算法能够较好地对特定辐射源进行分类识别，具有很好的工程应用前景。

2 UPMOP 特征曲线提取

2.1 相位观测模型

在不考虑脉冲压缩的情况下，双通道数字接收机被动接收到的一个雷达脉冲信号可以表示为

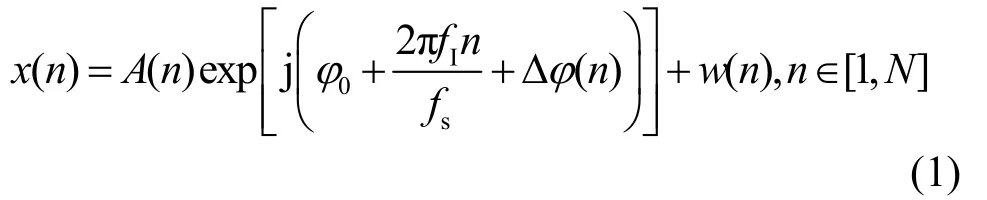
其中，A(n)为瞬时幅度函数，ϕ0为初始相位，fI为信号中心频率，fs为接收机采样频率，Δϕ(n)UPMOP，w(n)均值为0、方差为频率σ2的复高斯白噪声，N为采样点数。仅研究UPMOP 时，假定瞬时幅度恒定，可得信号相位观测模型[5]为

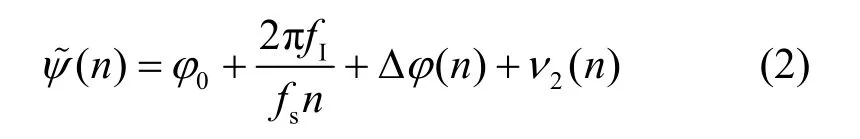
其中，ν2(n)是方差为的高斯白噪声；记，表示对(n)的直线拟合；记Δϕ(n)+ν2(n)为ρ(n)，表示UPMOP 的含噪估计。

2.2 提取流程

为从相位观测序列中提取UPMOP 特征曲线，首先需要进行去斜处理。文献[8]指出UPMOP 是一类随机噪声，均值为0，因此可利用最小二乘法拟合g(n) 来去除载频的影响。令

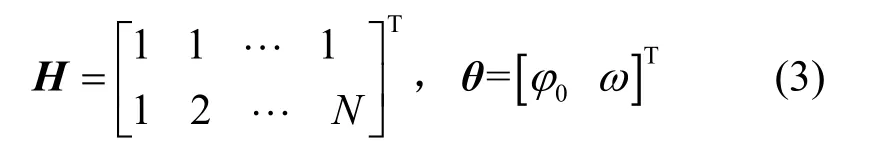
由于ρ是 UPMOP 的含噪估计，噪声造成UPMOP 特征曲线上下抖动明显，时序上变化迅速，不利于分类器学习到有效特征。为了得到UPMOP更精确的特征描述，本文采用贝塞尔曲线对UPMOP 进行平滑。贝塞尔曲线是图形学和数值分析中常用的参数曲线，它根据曲线的首末点和中间的控制点来构成曲线，d阶贝塞尔表达式为

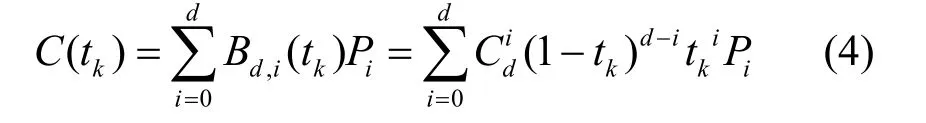
其中，tk为归一化时间参数，为d阶伯恩斯坦多项式；Pi为控制点；为二项式系数。贝塞尔曲线平滑相当于对UPMOP 含噪估计ρ=[ρ(1),ρ(2),…,ρ(N)]T进行插值拟合。将平滑贝塞尔曲线表示为C=[C(t1),C(t2),…,C(tN)]T=BN×(d+1)P(d+1)×1，平滑效果通过误差平方和进行衡量，则目标函数表示为

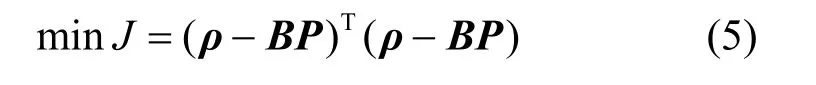
本文为了简化贝塞尔曲线的求解过程，仅将控制点作为待估计参数，并令时间参数,N，N为UPMOP 序列样点数，则式(5)可转化为线性最小二乘问题。可以解得控制点序列，平滑降噪后的UPMOP序列为。根据以上分析可知，UPMOP 特征曲线的提取流程如下。1) 对原始脉冲数据x进行相位解缠绕获得相位观测序列；2)利用最小二乘法对观测相位序列进行去斜处理，获得UPMOP 的含噪估计序列ρ；3) 进一步利用贝塞尔曲线拟合序列ρ进行平滑，获得UPMOP降噪序列。

3 识别算法

3.1 LSTM-FCN

本文利用UPMOP 特征曲线实现辐射源个体识别，实质上是一种时间序列分类问题，而时间序列分类是数据挖掘中一个重要且具有挑战性的课题。随着时间数据可用性的增加，研究人员提出了数百种方法来解决该问题，最流行和传统的方法之一是使用最近邻分类器和距离函数，如动态时间扭曲（DTW,dynamic time warping）距离函数[14]。但基于DTW 距离度量的最近邻分类算法计算复杂度高，在实际环境中的应用受限。近年来，深度学习在各种分类任务中取得了巨大成功，因此研究人员探索了将深度学习技术应用于时间序列分类问题，以便以端到端的方式从原始时间序列中学习隐式的判别特征。

文献[15]提出LSTM-FCN 等一系列模型用于解决时间序列分类问题，并在UCR 据集上验证了该模型的识别性能。LSTM[16]是一种特殊的循环神经网络（RNN,recurrent neural network），能够很好地解决长时依赖、RNN 梯度消失等问题，主要用于时间序列处理领域。与RNN 单一tanh 循环体结构不同，LSTM 是一种拥有3 个门结构的特殊网络结构，如图1 所示。

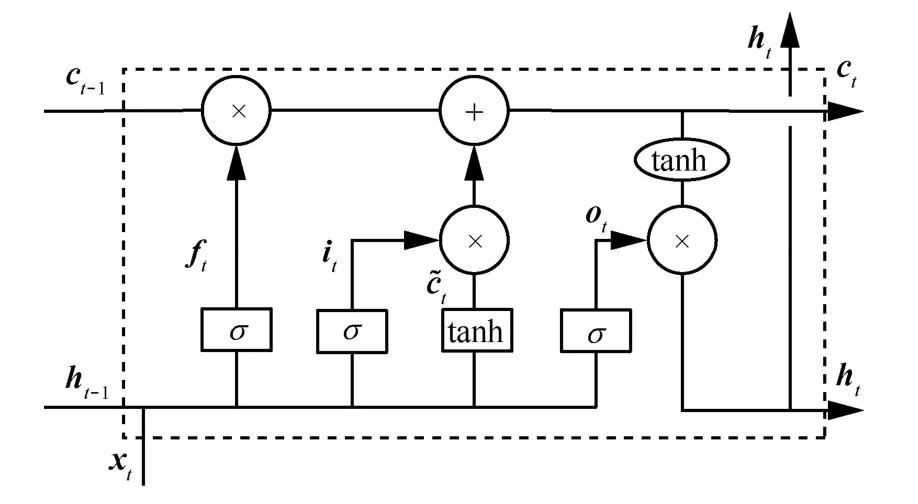
图1 LSTM 结构示意

LSTM 有2 个传输状态：细胞状态ct代表长时记忆，隐藏状态ht代表短时记忆。LSTM 的3 个门分别为遗忘门、输入门和输出门，遗忘门ft控制是否遗忘上一时刻的细胞状态ct−1，输入门it控制当前输入信息是否加入上一时刻状态生成新的细胞状态ct，输出门ot根据当前细胞状态ct控制当前时刻的隐藏层输出ht。ht−1表示上一时刻的隐藏层输出，xt表示当前时刻输入，σ表示sigmoid 激活函数，输出0～1 的数值，描述当前输入有多少信息可以通过门结构。

卷积神经网络（CNN,convolutional neural network）已成功应用于图像识别、自然语言处理等领域，研究人员开始将CNN 应用于时序分析领域。单变量时间序列使用一维卷积，也称时序卷积[17]。时序卷积与二维卷积的差别在于时序卷积的核尺寸是一个整数，表示一维卷积窗口的长度。假设时序卷积窗口长度为d，卷积核数量为K，步长为1，使用全0 填充以保持输出序列长度不变，对时间序列X进行时序卷积，输出为

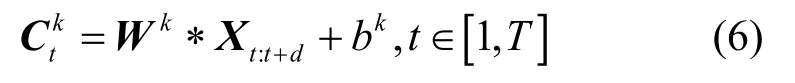
LSTM 利用网络中的循环结构挖掘样本的时序信息，每个时刻输出层的信息不仅和当前的输入有关，前一时刻的输出同样影响着该时刻的输出，具有序列建模的能力。而一维时序卷积对时间序列进行滑动加权滤波，中心时刻的输出值不仅与当前时刻输入值相关，而且与窗口内中心时刻的左右值相关，使用多个卷积核堆叠多个卷积层构成的FCN，则可以从不同层面挖掘时间序列的特征。LSTM 网络和FCN 都能较好地处理数据在时间维度上的关联性，因此，本文联合LSTM 和FCN 来自动提取UPMOP 序列的特征。

3.2 网络模型框架

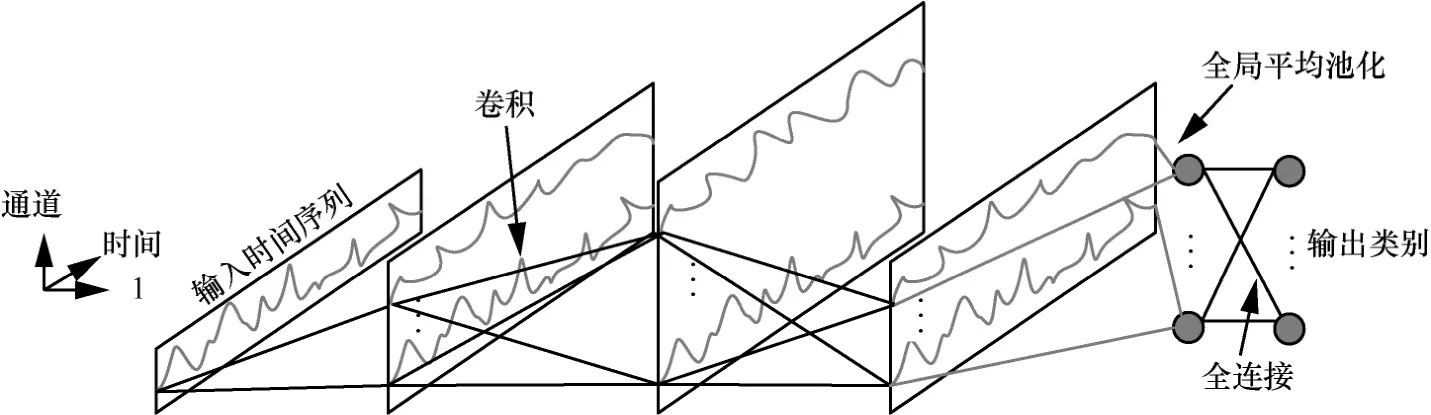
图2 FCN 结构用于时间序列分类

本文基于 Keras 搭建网络模型，图 3 为LSTM-FCN 模型结构。输入为UPMOP 特征曲线，LSTM 和FCN 分别从不同的角度提取UPMOP 序列特征；输入UPMOP 为1×N的单变量时间序列，其中N为时间采样点数，在该网络结构中FCN 将时间序列看作多个时间步长的单变量序列处理，而LSTM 将时间序列看作多变量单步长序列处理，以提高网络模型性能，因此利用Permute 层置换输入维度[15]。FCN 由3 个卷积块堆叠而成，每个块包含3 个操作，分别为时序卷积、批标准化（BN,batch normalization）和ReLU 非线性变换。卷积层卷积核数量分别为128、256、128，对应的卷积窗口长度分别为7、5、3，卷积步长均为1，并使用全0填充保持卷积后输出特征序列时间维度不变。每层做非线性变换前对激活输入值进行批标准化，以加快收敛速度，提高模型泛化能力。经过3 组卷积运算后，提取到128×N的特征矢量，然后在整个时间维度上进行全局池化，聚合产生128 个特征值，以减少模型中的参数量。LSTM 的units 参数设置为8，即输出8 个数据作为8 个特征，并利用Dropout 层使部分隐层节点失活，缓解过拟合的可能。最后将LSTM 提取的8 个特征值与FCN 提取的128 个特征值进行串联，整合为136 个节点后利用Softmax 层输出类变量的概率分布，得到分类结果。

3.3 算法流程

本文算法流程如下。

步骤1训练数据集生成。根据UPMOP 特征曲线的提取流程，提取辐射源数据库中脉冲信号的UPMOP 序列，生成有标签的训练数据集。

步骤2离线训练。构建LSTM-FCN 模型，并初始化参数设置，利用训练数据集对模型进行离线训练，当模型达到稳态后保存模型。

步骤3目标信号预处理。首先对宽带接收频段进行信号检测，然后利用分选技术对检测到的信号脉冲流进行分选，最后对分选出的脉冲信号按照UPMOP 特征曲线提取流程提取UPMOP 序列。

步骤4在线识别。用保存的LSTM-FCN 模型对预处理的目标信号的UPMOP 序列进行在线识别，得到个体识别结果。

4 实验结果与分析

4.1 特征曲线提取实验

本节通过仿真实验验证UPMOP提取流程的可行性和有效性，并比较本文贝塞尔平滑方法和文献[5]时域加窗平滑方法对UPMOP 的降噪性能。假设雷达发射脉冲的信号模型为

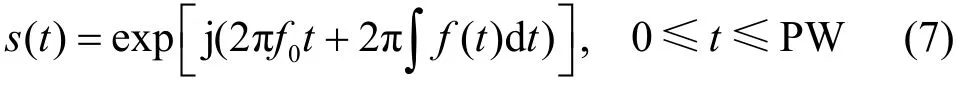
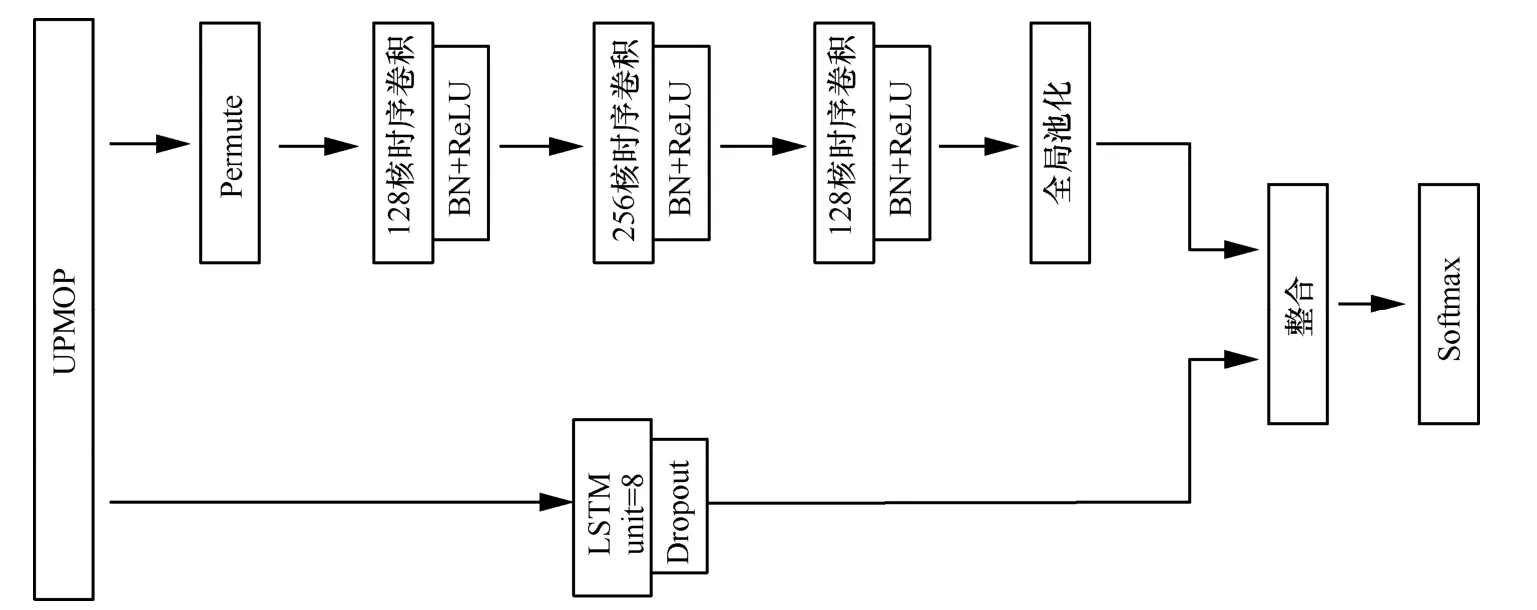
图3 LSTM-FCN 模型结构

其中，f0为信号载频，PW=0.5 μs为脉宽，f(t)=为正弦形式的脉内无调频函数，B=2 MHz 为频率调制带宽，利用相位第二项仿真UPMOP。产生数字仿真信号时，设信号经接收机下变频至中频，fI=60 MHz，fs=250 MHz，信号时间采样点数N为125。实验采用UPMOP 估计均方根误差（RMSE,root mean square error）来衡量降噪性能。

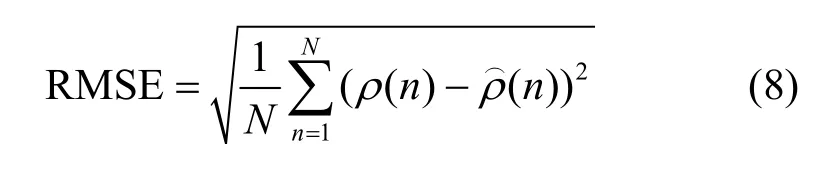
其中，ρ(n)表示时刻n提取的UPMOP 含噪估计值，表示n时刻降噪后的UPMOP 值。利用贝塞尔曲线对UPMOP 进行平滑降噪时，首先需要确定合适的贝塞尔阶数。当信噪比为25 dB 时，分别测试了1～8 阶贝塞尔降噪性能，每个阶数下均进行1 000 次蒙特卡洛仿真，统计均方根误差结果如图4(a)所示。可以看出，UPMOP 估计均方根误差随着贝塞尔阶数的增大而逐渐减小，当阶数为4 时均方根误差小于0.05 并趋于稳定，此时能够获得UPMOP 较为精确的特征描述。综合考虑降噪性能和计算复杂度，本文后续实验均采用4 阶贝塞尔对UPMOP进行平滑降噪。

对比2 种降噪方法时，令信噪比为10～45 dB，每隔5 dB 分别进行1 000 次蒙特卡洛仿真，计算不同信噪比下的均方根误差，统计结果如图4(b)所示。可以看出，信噪比越大，UPMOP 估计均方根误差越小，降噪性能越好，但在不同信噪比下，贝塞尔平滑后的估计均方根误差均低于时域加窗平滑后的误差。实验证明，本文算法能够有效提取UPMOP特征曲线，并且利用贝塞尔平滑方法能够获得UPMOP 更精确的特征描述。

4.2 仿真数据测试结果

本节通过仿真实验检验基于UPMOP 特性和LSTM-FCN 模型的个体识别方法的可行性与有效性，并与其他个体识别方法进行对比。仿真两部雷达，信号模型与式(7)相同，仅在频率调制带宽上有细微差别，B1=2 MHz，B2=B1+ΔB。利用LSTM-FCN 进行个体识别时，首先构造训练数据集对LSTM-FCN 进行离线训练以获得稳定模型，然后利用稳定模型对新的脉冲样本进行在线识别。当ΔB固定为0.3 MHz 时，在每个信噪比下两部雷达各产生10 个样本构成训练数据集；当信噪比固定为25 dB 时，在每个ΔB下两部雷达各产生80 个脉冲样本构成训练数据集。在不同信噪比及不同ΔB条件下，分别对两部雷达各1 000 个样本进行识别，统计5 种算法的平均识别正确率，结果如图5 所示。图5 中Beizer、smooth 分别表示贝塞尔平滑降噪和时域加窗平滑降噪，KNN-ED、KNN-DTW 分别表示基于欧氏距离和基于DTW 距离的最近邻识别算法，本文算法表示为Bezier-LSTM-FCN，文献[5]方法表示为smooth-KNN-ED。可以看出，贝塞尔平滑降噪法均有利于雷达辐射源个体识别，相比于时域加窗平滑降噪法能够获得更高的识别正确率；无论基于欧氏距离还是基于DTW 距离度量的最近邻识别算法性能均不如LSTM-FCN。图5(a)表明，当SNR <25 dB时，本文算法能够取得较其他方法更高的识别正确率，对噪声的稳健性更强。图5(b)表明，在相同信噪比条件下，本文算法能够更好地区分相似目标。基于以上分析可知，本文算法可行有效，并且在不同信噪比或者不同ΔB条件下本文算法识别性能更优。

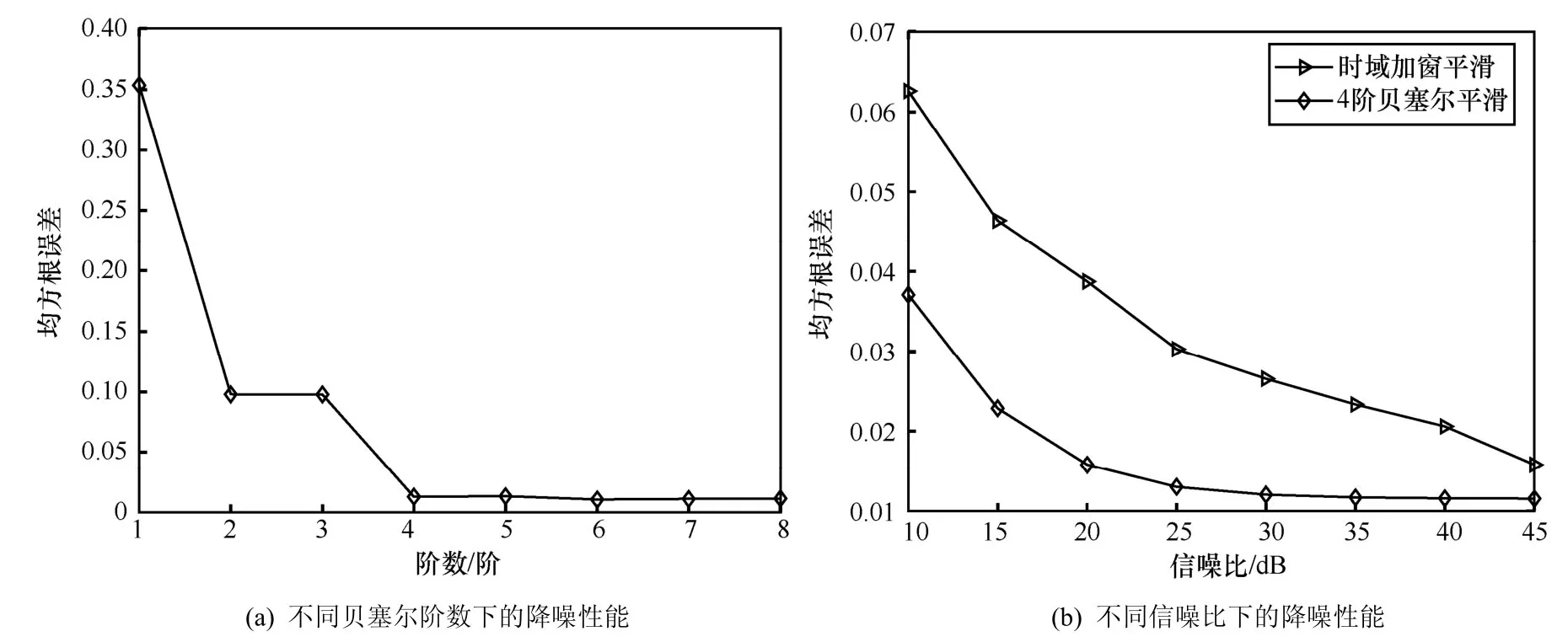
图4 降噪性能分析

图5 不同方法识别性能对比

4.3 网络参数对性能的影响

本节分别从网络结构和训练数据量2 个角度测试网络参数对识别性能的影响。首先比较LSTM-FCN、LSTM 和FCN 这3 种网络结构对个体识别性能的影响。当ΔB固定为0.3 MHz 时，在不同信噪比下两部雷达各产生10 个样本构成训练数据集，3 种网络训练稳定后分别对两部雷达各1 000个样本进行识别，结果如图6(a)所示。可以看出，LSTM-FCN 模型能够获得更高的识别正确率，识别性能优于单独使用 LSTM 或 FCN，表明LSTM-FCN 能够从不同的角度提取UPMOP 序列特征，形成更丰富的联合特征表示，特征刻画能力强，因此识别性能更优。训练数据量的大小同样对个体识别性能产生影响。在不同训练数据量下，训练获得稳定模型后分别进行个体识别实验，每次实验对两部雷达各1 000 个样本进行识别，统计平均识别正确率，实验结果如图6(b)所示。可以看出，信噪比越低，训练数据量的大小对识别正确率的影响越大；并且随着训练数据的增加，个体识别正确率也逐渐增加。但当训练数据量超过160 个样本时，在不同信噪比条件下识别正确率已趋于稳定，即在样本数量较少的情况下，本文算法仍具有优异的分类性能，对雷达辐射个体识别具有重要意义。

4.4 实测数据测试结果

图6 不同网络参数下的识别性能对比

本文实验利用信号源A、B、C 模拟雷达发射机发射信号，利用实时频谱分析仪进行信号采集，其中，信号源A、B、C 型号分别为Tektronix AWG70002A、Tektronix AWG70002B 和Agilent E8267D，实时频谱分析仪型号为 Tektronix RSA5126B。信号源A、B、C 发射脉冲脉宽均为1 μs，载频均为1 GHz，实时频谱分析仪分别采集存储每个信号源500 个脉冲进行实验，采样频率为200 MHz，信号时间采样点数N为200。采用实时频谱分析仪直接以馈线的方法进行信号采集，因此在信号传播过程中几乎没有加入新的噪声，采集的信号具有较高的信噪比。从采集的脉冲中各随机选择100 个脉冲样本，提取UPMOP特征曲线如图7 所示。可以看出，不同个体均存在UPMOP，并且UPMOP 能够体现不同个体独有属性，因此在实际工程应用中利用UPMOP 特性实现个体识别是可行的。

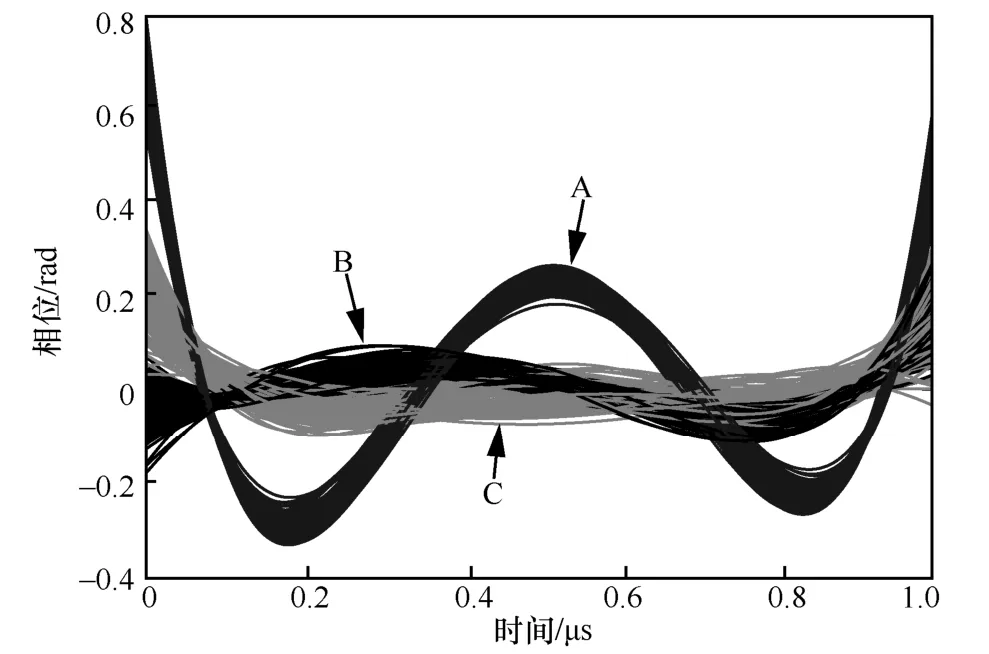
图7 3 个信号源各100 个脉冲的UPMOP 特征曲线

随机选取 3 个信号源各 80 个脉冲提取UPMOP 序列作为训练样本集，剩余1 260 个脉冲作为测试样本集，识别时分别采用基于欧氏距离的最近邻算法、基于DTW 距离的最近邻算法和本文算法LSTM-FCN。实验进行100 次，得到各算法平均识别耗时和平均识别正确率如表1 所示。从表1 中可以看出，本文算法能够取得更高的识别正确率，平均识别耗时较短。因此，综合考虑可得本文算法性能更优，具有较好的工业应用前景以及研究价值。

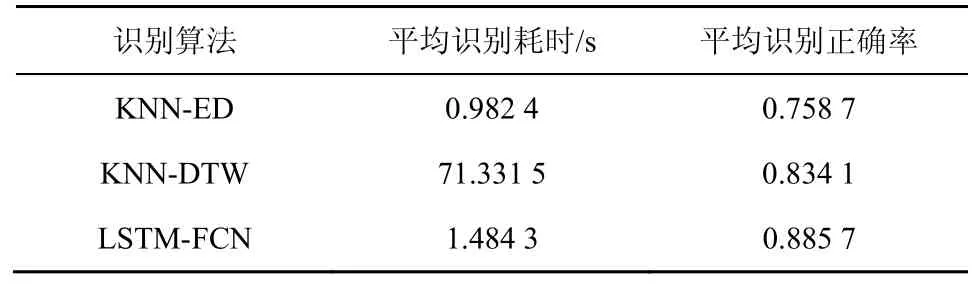
表1 不同分类算法对实测数据的分类性能比较

5 结束语

本文提出了一种新的基于UPMOP 特性的雷达辐射源个体识别算法，能够准确地识别雷达辐射源个体。该算法借助贝塞尔曲线拟合获得了UPMOP 更为精确的特征描述，引入深度学习技术，构建LSTM-FCN 模型自学习UPMOP 时间序列特征，实现了雷达辐射源个体分类识别，有效解决了传统最近邻算法在时间序列分类问题上表现不佳的问题。实验证明，本文算法对噪声和样本数量均具有较好的稳健性，运算耗时短，性能优。本文将深度学习技术引入雷达辐射源个体识别领域中，为解决雷达辐射源个体识别问题提供了新的思路。