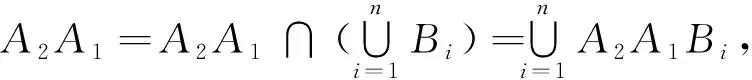全概率公式的推广及应用
2020-06-05兰瑞平
兰瑞平
(吕梁学院 数学系,山西 离石 033001)
全概率公式是概率论的一个重要公式,在概率计算的问题中有着举足轻重的作用.它化繁就简,使一些复杂事件的概率的计算简单化.但是由于其条件比较严格,在实际问题中有时难以满足,因此需要将其条件进行弱化,使之成为解决复杂事件概率计算的实用性工具;另外,将全概率公式在条件概率下进行推广,可以扩大其使用范围.
以下内容介绍全概率公式的四种推广形式,并通过具体的例子介绍其应用.首先介绍基本概念.
定义(划分)[1]设(Ω,F,P)为概率空间,若事件列Bi∈F,i=1,2,…,n满足:
(2)B1,B2,…,Bn两两互斥,即BiBj=∅ ,i≠j,i,j=1,2,…n;
则称B1,B2,…,Bn为Ω的一个划分(或分割),称B1,B2,…,Bn为完备事件组.
引理1 (全概率公式)[1]设(Ω,F,P)为概率空间,若事件列B1,B2,…,Bn是Ω的一个划分,且P(Bi)>0,i=1,2,…,n,则对∀A∈F,有
将定义与引理1合并,表述为引理1′.
引理1′(全概率公式)[1]设(Ω,F,P)为概率空间,若Bi∈F,i=1,2,…,n.满足:
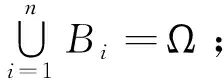
(2)BiBj=∅,i≠j,i,j=1,2,…n;
(3)P(Bi)>0,i=1,2,…,n;
则对∀A∈F,有
注:全概率公式中,对Ω进行划分的事件个数n可以是,见参考文献[2].
下面对引理1′中的条件进行不同形式的弱化,得到推广的全概率公式.
1 对条件的弱化
定理1[1,3]设(Ω,F,P)为概率空间,若∀A∈F,Bi∈F,i=1,2,…,n,满足:
(2)BiBj=∅,i≠j,i,j=1,2,…n;
(3)P(Bi)>0,i=1,2,…,n;
则有
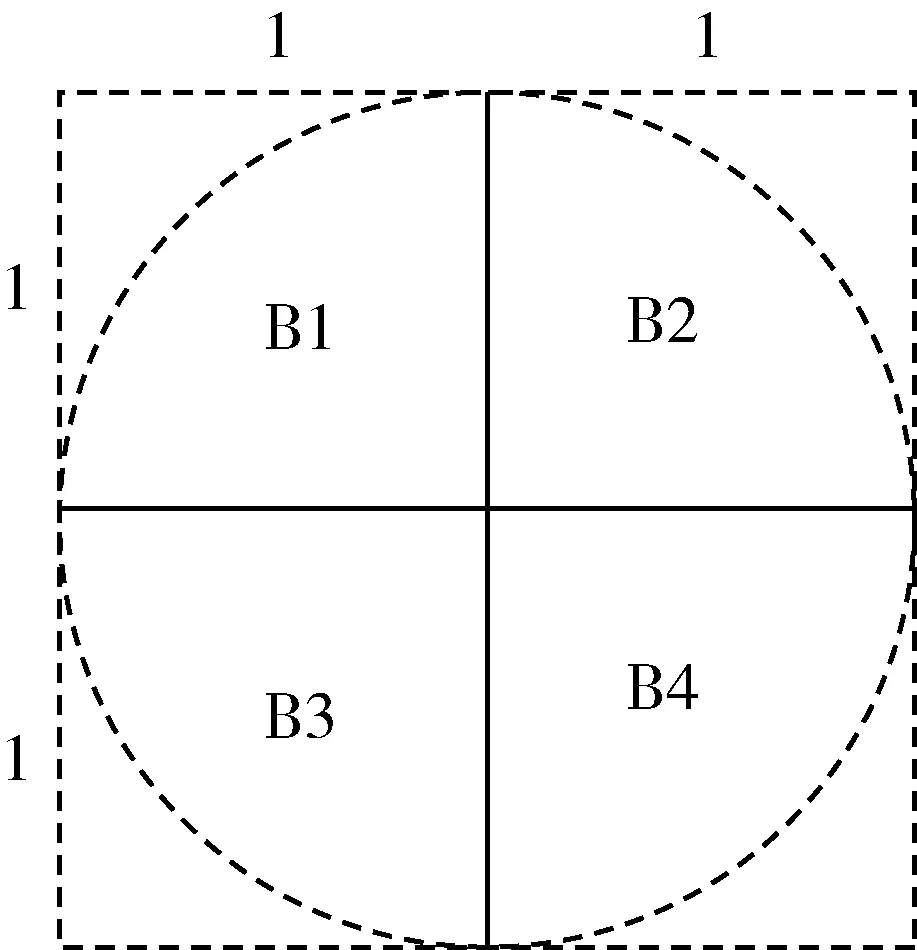
图1
例1向某平面区域内随机投点,随机点落入边长为1的小正方形区域Bi,i=1,2,3,4内的概率分别是0.1,0.2,0.2,0.3,落到大正方形区域(B1∪B2∪B3∪B4)外的概率为0.2,如图1.当随机点落入区域Bi,i=1,2,3,4时,随机点在Bi,i=1,2,3,4区域中服从均匀分布.试求平面上的随机点落入大正方形内接圆内的概率.
解:记A为事件“平面上随机点落入内接圆”,记Bi为事件“平面上随机点落入区域Bi”,i=1,2,3,4.由题意知圆的半径为1,故圆的面积为π.且
P(B1)=0.1,P(B2)=0.2,P(B3)=0.2,P(B4)=0.3,
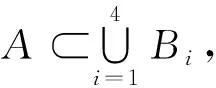
2 对条件“事件列B1,B2,…,Bn两两互斥”的弱化1
在实际问题中,有时不容易找到两两互斥的事件列,往往事件列之间的关系是相容的,但若其相容的概率为零,则可以改变全概率公式的限制条件,进而扩大其应用范围.
定理2[4]设(Ω,F,P)为概率空间,若事件列Bi∈F,i=1,2,…,n满足:
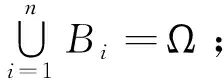
(2)P(BiBj)=0,i≠j,i,j=1,2,…n;
(3)P(Bi)>0;
则对∀A∈F,有
证明: ∀A∈F,由条件(1)知
由概率的加法公式可得
而当i≠j时有P(BiBj)=0,从而有
P(ABiBj)=0,…,P(AB1B2…Bn)=0,
所以
由定理2的条件可知,只需要P(BiBj)=0,i≠j,而未必要求B1,B2,…,Bn两两互斥,全概率公式仍然成立.
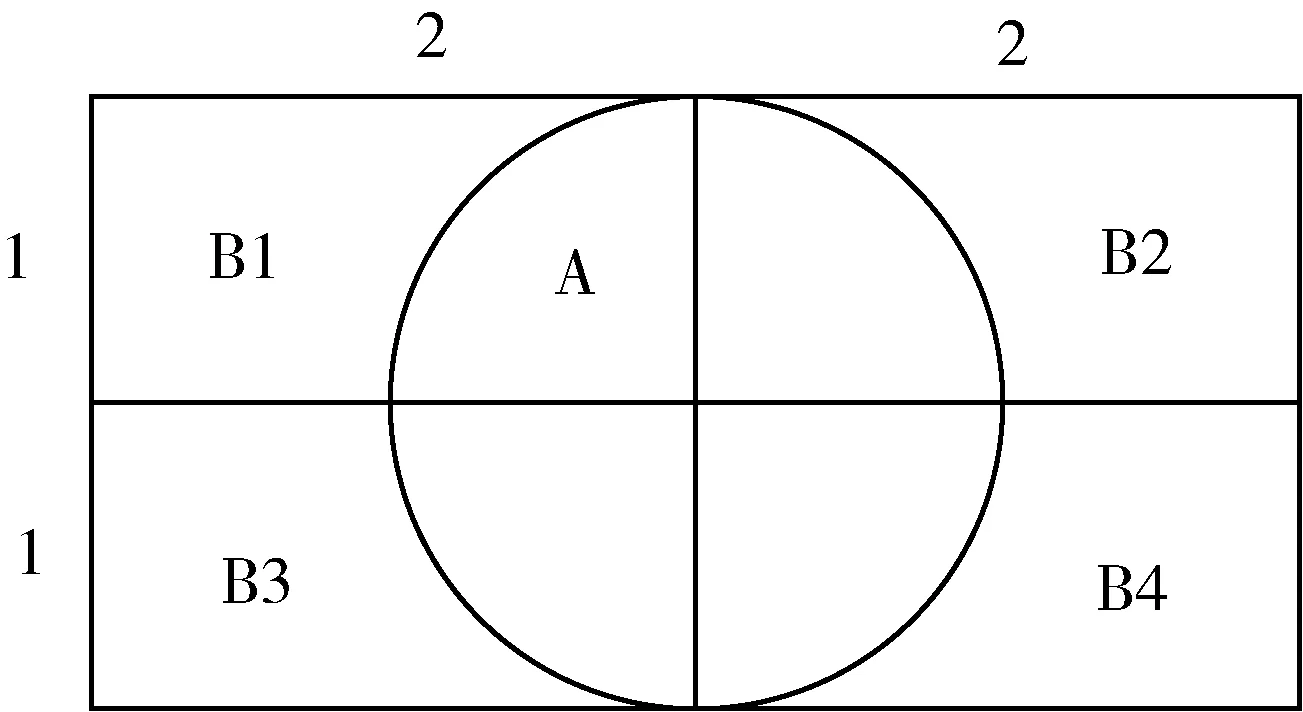
图2
例2向平面上的区域随机投点,如图2.随机点落入闭矩形区域Bi,i=1,2,3,4内的概率分别是0.2,0.3,0.2,0.3.当随机点落入区域Bi时,点在该区域中服从均匀分布.试求随机点落入圆A内的概率[4].
解:记A为事件“平面上随机点落入圆A内”,Bi为事件“平面上随机点落入区域Bi内”,i=1,2,3,4.依题意知圆的半径为1,故圆的面积为π.由于B1,B2,B3,B4都是闭矩形区域,显然BiBj≠∅,i≠j,i,j=1,2,3,4, 但是P(BiBj)=0,i≠j,i,j=1,2,3,4.依题意,有
P(B1)=0.2,P(B2)=0.3,P(B3)=0.2,P(B4)=0.3,
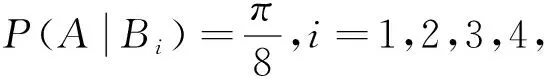
在这个问题中,由于B1,B2,B3,B4都是闭矩形区域,故其两两之间是有交集的,其交集就是图形与图形之间的交线.又由几何概型得其概率为P(BiBj)=0,i≠j,i,j=1,2,3,4,满足定理2的条件.
3 对条件“事件列B1,B2,…,Bn两两互斥”的弱化2
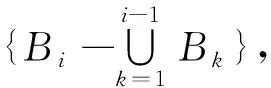
定理3[4]设(Ω,F,P)为概率空间,Bi∈F,i=1,2,…,n.如果有
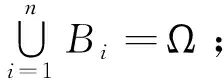
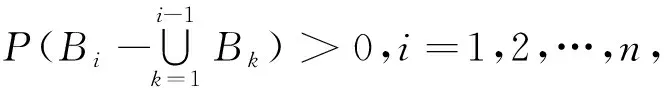
则对∀A∈F,
证明:要证明定理成立,只需要证明
先证明(i).由于
B1∪(B2-B1)=B1∪B2,(B1∪B2)∪(B3-(B2∪B1))=B1∪B2∪B3,
以此类推,可得
对于(ii),由于i≠j,不妨设i 定理1、定理2中证明的全概率公式的推广形式都有三个限制条件,而定理3中的推广形式既不需要事件列两两互斥,也不要求其概率为零.只需后一事件减去前面事件和之后的事件概率大于零即可.在一些情况下,此推广形式使用更加方便. 例3有王军、陈亮、张剑三名士兵同时向天空中同一飞行方向的目标进行射击,这几名士兵分别击中的概率是0.3,0.6,0.8.假设三人中只有一人击中,那么这一飞行目标被击落的概率是0.2;假设三人中有两人击中,那么这一飞行目标被击落的概率为0.6;假设三人均击中,那么这一飞行目标就会被击落,试求该飞行目标被击落的概率[4]. B0= “三人都未击中飞行目标”, B1-B0= “三人中只有一人击中飞行目标”, B2-B1-B0= “三人中只有两人击中飞行目标”, B3-B2-B1-B0= “三人都击中飞行目标”. 为两两互斥事件.由三人射击的独立性可得 P(B0)=0.056,P(B1-B0)=0.332, P(B2-B1-B0)=0.468,P(B3-B2-B1-B0)=0.144, 又有 P(A|B0)=0,P(A|B1-B0)=0.2 P(A|B2-B1-B0)=0.6,P(A|B3-B2-B1-B0)=1. 由定理3可得 P(A)=P(B0)P(A|B0)+P(B1-B0)P(A|(B1-B0))+P(B2-B1-B0)P(A|(B2-B1-B0))+ P(B3-B2-B1-B0)P(A|(B3-B2-B1-B0)) =0.056×0+0.332×0.2+0.468×0.6+0.144×1=0.3616. 即飞行目标被击落的概率为0.3616. 注:本题也可以直接使用定理1中的全概率公式求解. 之前的推广都是“原因直接产生结果”的模型,但有些随机事件的结果并非由原因直接导致的,而是由一系列中间变化的过程得到的,求解这类问题实际就是在条件概率下对全概率公式进行推广. 定理4[5]设(Ω,F,P)为概率空间,B1,B2,…,Bn为一个完备事件组,则对∀A1⊂Ω,∀A2⊂Ω,且P(A1Bi)>0,i=1,2,…,n,有 于是有 定理得证. 注:此定理的详细说明可参考文献[5]. 显然,当事件A1与Bi,i=1,2,…,n相互独立时,有以下推论. 推论设(Ω,F,P)为概率空间,B1,B2,…,Bn为一个完备事件组,则对∀A1⊂Ω,∀2⊂Ω,且A1与Bi,i=1,2,…,n相互独立,P(A1Bi)>0,i=1,2,…,n,有 例4某工厂为了了解车间的生产情况,从三个车间分别抽取了20,25,30个产品进行检验,其中一等品分别为4,5,8个.现随机选定一个车间的产品,并从中先后不放回地任意选取2个产品.(1) 求第一次取到的是一等品的概率.(2) 已知第一次取到的是一等品,求第二次取到的产品也是一等品的概率. 解:记Ai={第i次取到一等品},i=1,2;Bj={选取的是第j个车间},j=1,2,3. (1)由全概率公式有: P(A1)=P(B1)P(A1|B1)+P(B2)P(A1|B2)+P(B3)P(A1|B3)= (2)由题意知 P(A2|A1)=P(B1|A1)P(A2|A1B1)+P(B2|A1)P(A2|A1B2)+P(B3|A1)P(A2|A1B3)= 其实,在有关概率和随机模型的研究中,凡是涉及到用概率分析的方法,全概率公式几乎都会被使用.那么能够灵活使用全概率公式就会为解题提供很大的方便,本文通过几种推广形式进一步扩大了全概率公式的使用范围,使其真正成为我们解决问题的有效工具.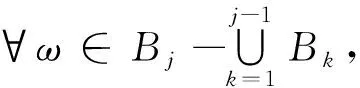
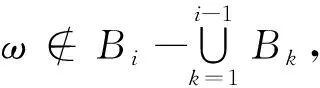
4 全概率公式在条件概率下的推广