基于分数阶微分算子的数字图像边缘检测

郭琳琴，杨 艳，马浩东

(吕梁学院 数学系，山西 离石 033001)

0 引言

图像的边缘中包含了丰富的视觉信息，在图像分割、图像特征提取、模式识别中有重要的意义，图像的边缘检测是图像处理中应用最为广泛的研究课题之一.传统的边缘检测算子多为微分算子，主要包括Rebort算子、Sobel算子等一阶微分算子和Lapllician算子、LOG算子等二阶微分算子.

近年来，分数阶微分算子被广泛应用于图像处理过程中，并逐渐成为一个研究热点.文献[1]中杨柱中等人提出一种基于0～1阶分数阶微分的Tiansi掩模算子，该算子可有效的提取图像的边缘信息且有较高的信噪比；文献[2]中王卫星等人进一步的改进了Tiansi掩模算子，使得图像的边缘检测中纹理细节得到有效增强；汪成亮等人在文献[3]中针对分数阶数阶数需要人为指定的缺陷，提出了一种自适应的算法；文献[4]中蒋伟等人为了在锐化图像边缘的同时增强纹理细节特征，结合分数阶与整数阶微积分理论，推导出了新的有理数阶微分.

本文提出的分数阶图像边缘检测模型，将能量泛函式中的导数改为分数阶导数，然后用差分格式对其进行逼近求解从而分别构造水平、垂直和对角线分数阶边缘检测微分算子，最后将这些算子合成为新的分数阶边缘检测算子.

1 相关理论

1.1 分数阶导数

分数阶导数目前有三种经典定义：Riemann-Liouville(R-L)、Capotu(C)和Grumwald-Letnikov(G-L)，其中 G-L分数阶导数定义为

(1)

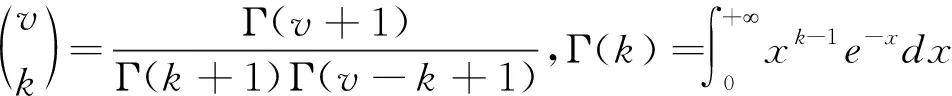
1.2 分数阶导数的差分格式

式(1)中h=1时，G-L分数阶导数可以用有限项的分数阶差分近似表示，即：

(2)

将上式推广到二维，即可得到f(x，y)的分数阶偏导数定义：

(3)

(4)

进一步可得差分近似表达式：

特别地，当v=1时，上式变为一阶微分的差分近似表达式，

当v=2时，上式变为二阶微分的差分近似表达式，

可见分数阶微分是一阶与二阶微分的推广形式.

2 基于分数阶的图像边缘检测算子

2.1 模型的建立

引入文献[5]中能量泛函式：

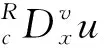
利用变分法推得的该泛函欧拉-拉格朗日方程如下：

其中，

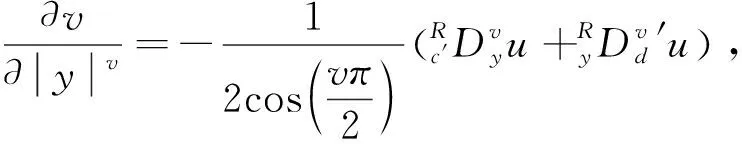
则，有如下结果

(5)

(6)

(7)

利用梯度下降法得到相应的扩散方程：

(8)

对上式离散化，有

其中，

2.2 分数阶微分算子构造

构建水平方向和逆对角线方向整数阶掩模算子，如图1.

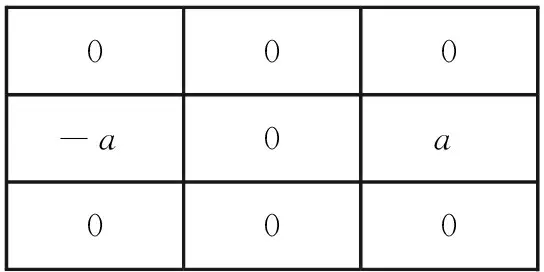
000-a0a000

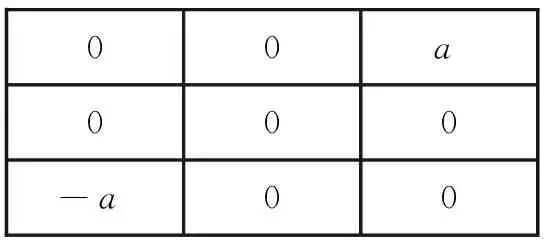
(a)水平方向整数阶算子

(b)逆对角线方向整数阶算子

图1水平方向和逆对角线方向上的整数阶算子

以图1(a)构造微分算子：a(f(x+1，y)-f(x-1，y))

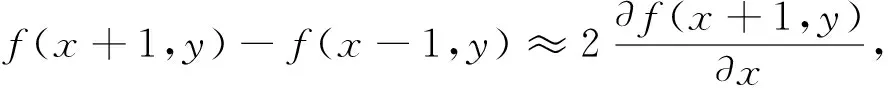
则有x轴方向分数阶微分算子如图2(a)所示，旋转对称可构造y轴方向大小为3×3的分数阶微分算子，如图2(b)所示.

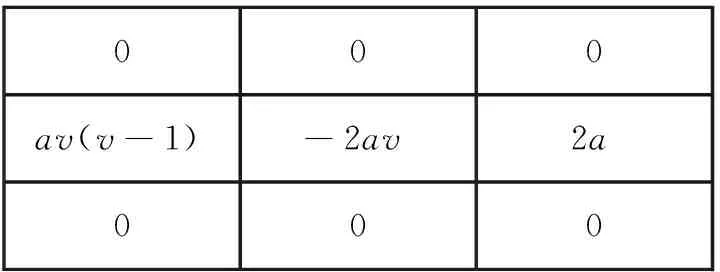
000av(v-1)-2av2a000

(a)x轴方向上的分数阶算子

(b)y轴方向上的分数阶算子

图2水平、垂直方向上的分数阶微分算子

以图1(b)构造微分算子：a(f(x+1，y-1)-f(x-1，y+1)),有G=a(f(x+1，y-1)-f(x-1，y+1))

为了使得具有对称性，做如下变形

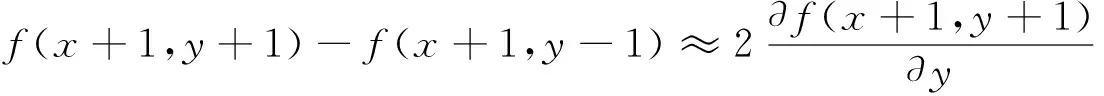
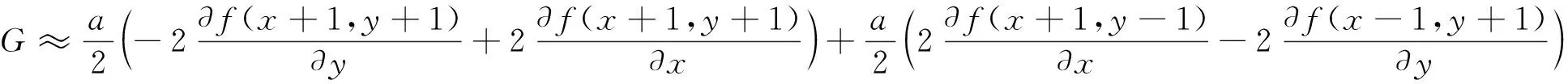
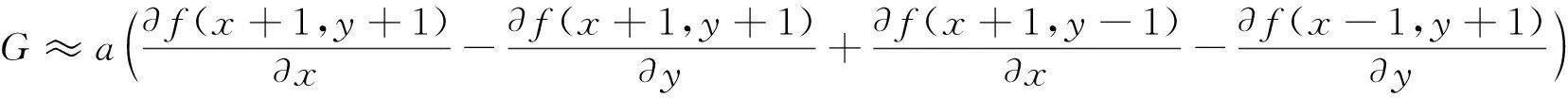
化解后可得

即可得逆对角线上分数阶算子如图3(a)，旋转对称可构造正对角线上的分数阶算子如图3(b).

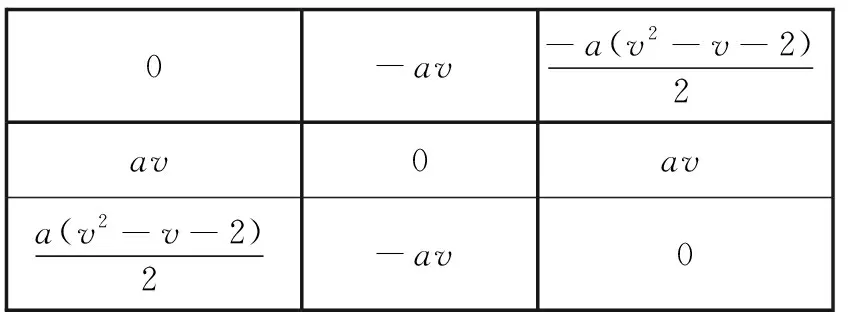
0-av-a(v2-v-2)2av0ava(v2-v-2)2-av0

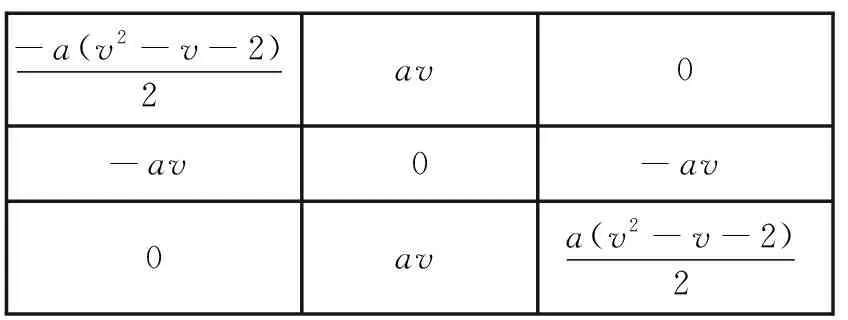
(a)逆对角线方向上的分数阶算子

(b)正对角线方向上的分数阶算子

图3不同方向上的分数阶微分算子

将所得的4个微分算子相加，即可得到3×3的分数阶微分算子w，如图4所示.

-a(v2-v-2)2-av(v-1)-a(v2-v-2)2av(v-1)02aa(v2-v-2)2-2aa(v2-v-2)2

图4分数阶微分算子w

2.3 基于分数阶微分算子的边缘检测

设g(x，y)为灰度图像函数，利用分数阶微分算子w对图像进行边缘检测的具体过程如下：

step1 对图像g(x，y)进行去噪声预处理，得到g(x，y)；

step2 选取适当的v，利用分数阶微分算子w对图像g(x，y)进行卷积运算，得到e(x，y)；

Step3 选取适当的阈值，对e(x，y)进行二值化处理，即可得到最终的边缘检测结果a；

该过程中，分数阶参数v的选择决定图像边缘检测的效果，在实际操作中需要多次实验调整.

3 实验结果

实验在MATLAB2019软件环境下选取图5(a)作为原图完成.得到不同a值和不同v值下的图像边缘检测结果，如图5和图6.

图5 不同v取值下图像边缘检测实验结果

图6 不同a取值下图像边缘检测实验结果

图5实验是在a=3时选取不同的v检测的结果，可以看出当v值从0.4开始接近于0.7时边缘检测结果逐渐变好，可以较好的检测到图像的边缘，当v值大于0.7时边缘检测结果清晰度略有下降，可见本文算法在合适的v值下的边缘结果可以保留原图像的特征，在视觉上有较好的效果.

图6实验是在v=0.7时选取不同的a值检测的结果，可以看出当a值逐渐增大时边缘信息逐渐增多，但当a选取过大时则会引起背景区域中的伪边缘较为明显的情况.

4 结束语

本文提出了一种基于分数阶偏微分方程的图像边缘检测模型，模型中将整数阶微分算子中的二阶导数变分为分数阶导数，从而构造了包含水平、垂直、正对角线、负对角线四个方向梯度的分数阶微分算子.实验仿真结果表明，该算子能较好保留图像的边缘信息和纹理细节特征，对弱纹理图像也可得到较为清晰的边缘检测结果，是一种可行的数字图像边缘检测算法模型.实验结果还表明检测过程中的参数需要多次调整，如何自适应地选取参数以保证较好的检测效果仍有待进一步讨论研究.