基于多尺度结构特征的快速异源图像匹配
2020-06-05张皓,李娜,王陆
张 皓,李 娜,王 陆
〈图像处理与仿真〉
基于多尺度结构特征的快速异源图像匹配
张 皓1,李 娜1,王 陆2
(1. 河南工学院 计算机科学与技术学院,河南 新乡 453000;2. 北京邮电大学 电子工程学院,北京 100876)
针对异源图像提出一种基于多尺度密集结构特征的快速匹配算法。算法首先利用Gabor滤波器逐像素提取图像中的结构响应,再根据主方向响应对多尺度结构特征融合,然后使用快速傅里叶变换在频域计算各特征分量图像之间的卷积,最后将卷积生成的系数矩阵求和计算出图像之间的相似性并选择相似性最大位置作为匹配结果输出。本文算法能有效适应异源图像间的非线性灰度变化和噪声干扰问题。测试使用可见光、红外、雷达图像组成的异源图像数据集对本文算法和现有算法进行测试比较,结果表明:本文算法的平均误匹配率最低,并且计算速度有明显优势。
异源图像匹配;卷积定理;快速傅里叶变换;密集特征;Gabor滤波器
0 引言
异源图像匹配是指匹配的两张图像由不同类型图像传感器获取。异源图像匹配在导航制导[1]、目标定位[2]、图像融合[3]等视觉任务中被广泛应用。由于不同传感器的成像特性不同导致图像间存在明显的辐射畸变,这使得异源图像匹配成为一项非常具有挑战性的任务。一方面,辐射畸变可能导致一幅图像中出现的视觉特征不会出现在另一张图像中,从而增加特征匹配的难度。另一方面,辐射畸变引起的非线性灰度失真,使得异源图像之间的灰度映射非常复杂,这将严重降低直接基于灰度的图像匹配算法的性能。
遥感异源图像匹配还可能遇到噪声干扰带来的挑战。噪声通常在遥感影像中不可避免的,特别是红外影像和合成孔径雷达(Synthetic Aperture Radar, SAR)影像常常包含严重的噪声。由于噪声削弱了异源图像间相同对象的灰度之间的关联性,直接基于灰度的相似性测量准则将会受到影响。此外,结构特征提取方法往往对噪声非常敏感,这会降低基于图像结构信息的图像匹配的性能。
现有的图像匹配算法往往无法有效适应异源图像间的非线性灰度畸变或图像噪声的干扰。对此,本文提出一种基于多尺度密集结构特征的快速异源图像匹配算法。本文算法是属于模板匹配算法,如图1所示。这类模板匹配算法在导航和目标定位中常常使用。匹配前,拍摄图像(作为模板图)可以根据导航信息进行矫正,消除旋转和缩放后,模板图与基准图之间主要存在平移差别。
图2给出了本文算法的流程图。算法首先利用Gabor核提取图像结构特征,以适应异源图像间的非线性灰度畸变;然后对结构特征进行多尺度融合以提升抗噪声能力,最后利用快速傅里叶变换(fast Fourier transform, FFT)实现快速匹配。

图1 基于模板的异源图像匹配
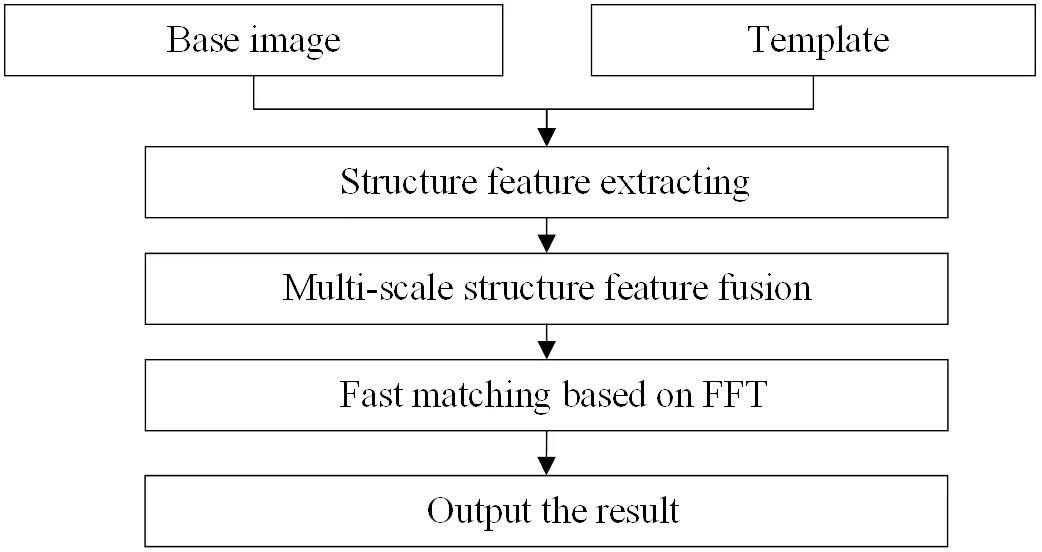
图2 本文匹配算法流程
现有异源图像匹配算法大致可以分为两类,一类通过改进差别/相似性测量准则来提高算法对非线性灰度畸变的适应能力。另一类通过提取图像结构信息来避免灰度畸变对匹配的不利影响。
改进测量准则的算法通常是假设成像条件造成的灰度畸变满足某种变换模型,若使测量准则忽略符合变换模型的灰度畸变,可以获得不受成像条件影响的相似性或差别测量方法,代表算法包括基于归一化互相关(normalized cross correlation, NCC)[4]、互信息(mutual information, MI)[5-6]和非线性调色原理(matching by tone mapping, MTM)的图像匹配算法[7]。其中,NCC是一种能够适应线性灰度畸变的测量准则。对属于单调非线性函数的灰度畸变,NCC也具有一定的适应性(因为非线性的灰度畸变往往可以看作局部线性的),并且可以采用Log-NCC提升适应能力[8]。MTM是一种能适应非单调非线性灰度畸变的图像匹配算法,但是仍然要求灰度畸变满足函数映射关系(不同灰度级不能映射到相同灰度级)。MI算法则基于信息熵的原理,它可以适应不满足函数映射关系的非线性灰度畸变,但是一些研究指出MI算法计算速度太慢,并且不适用于样本量较小的情况(即图像较小)。
仅仅改进匹配的测量准则并直接对灰度图像进行匹配,效果往往不太理想,因为这忽略了图像的纹理结构信息。鉴于此,一些匹配算法先使用密集特征描述(dense feature descriptor, DFD)提取图像中的纹理结构信息得到本征图像(intrinsic image),然后再对本征图像进行匹配。由于图像中的结构特征通常能够相对成像条件变化保持稳定并且密集特征描述一般不需要对灰度畸变的模型进行假设,基于本征图像提取的异源图像匹配算法往往在适应灰度畸变的能力上具有优势。现有的本征图像提取算法可以分为基于梯度[9-10]的和基于相位[11-12]的两类算法。基于梯度的提取算法能够适应图像对比度和照度的变化,并能有效提取适应图像的结构方向信息,但是灰度反映射(常常发生在异源图像间)会导致方向反转,影响相似评价[12]。基于相位的提取算法,能适应各种灰度畸变,但是无法准确提取图像的结构方向信息,并且可能导致混淆效应[13]。除此之外,两类提取算法都对噪声比较敏感,对于极具挑战性的异源图像匹配(如SAR图像和可见光图像之间的匹配),这两类算法往往都无法取得较高的匹配正确率。
1 多尺度结构特征提取
图像中对象的结构信息通常不因传感器类型和参数变化而改变,因此,结构可以作为异源图像间的共性特征。但是基于梯度和相位的结构特征提取算法对图像噪声的适应性不佳,很难稳定地提取结构特征。
算法首先利用Gabor滤波器逐像素提取图像中的结构响应,再根据主方向响应对多尺度结构特征融合,可以有效适应异源图像的非线性灰度畸变和图像噪声问题。
1.1 密集结构特征
Gabor滤波器可以分为奇滤波器和偶滤波器,其中奇数滤波器近似一种平滑的求导滤波器。比较常用的sobel求导算子[13-14],使用Gabor奇滤波器对图像求导具有更好的噪声适应能力。本算法使用8个方向的Gabor奇滤波器对图像求导,公式(1)给出了图像求导计算过程:
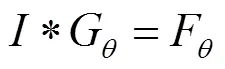
式中:是原图像;*代表卷积;是方向为的Gabor奇滤波器;是方向的导数。其中Î{0,p/8,p/4,p/2,5p/8, 3p/4,7p/8}。
求导后,图像每个像素对应一个8值的特征向量为F¢,将该特征向量取绝对值再按公式(2)进行归一化,可以消除灰度畸变对特征提取结果的影响:

1.2 多尺度结构特征融合
噪声会对基于求导的结构特征提取造成不利影响。多尺度特征融合,可以有效增强结构特征对噪声的适应能力。多尺度特征融合分为两个主要步骤。
首先对归一化结构特征按公式(3)进行均值处理,均值窗口可以选择以为中心,大小为×的窗口,即是特征尺度:
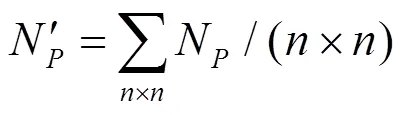
然后按公式(4)根据主方向响应强度,融合多个尺度的特征:
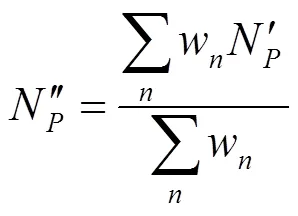
式中:w是主方向响应强度,可以按公式(5)计算:
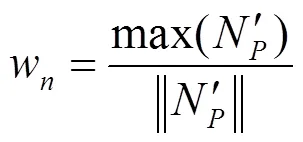
当一个方向的Gabor奇滤波器的响应明显大于其他方向时,主方向响应强度越大。
2 结构特征匹配
得到模板图像和基准图像的多尺度结构特征后,将模板图像与基准图像的每个窗口进行比较,选择相似性最大的窗口作为匹配结果。其中相似性计算是根据每个像素对应的特征向量计算,而不是图像灰度。设模板每个像素对应的特征向量为TN²,窗口每个像素对应的特征向量为WN²,则相似性按如下公式计算:
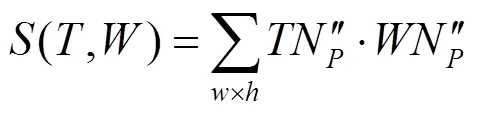
式中:模板图与窗口大小为×;×代表向量之间的点乘。
公式(6)可以按照两种过程计算,一是先计算特征向量之间的点乘再逐像素累加,二是先计算模板与窗口特征分量图之间的相关,再累加相关结果。两种计算方法的计算量都非常大。设基准图大小为×,则这两种计算方法的复杂性为:
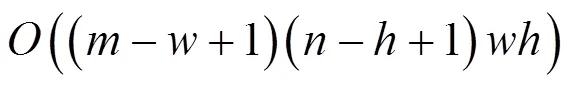
为了减少计算量,可以使用卷积定理对匹配过程进行计算优化。根据卷积定理,基准图像和模板图像之间的卷积可以通过它们在频域的乘积的反傅里叶变换得到,过程如下:
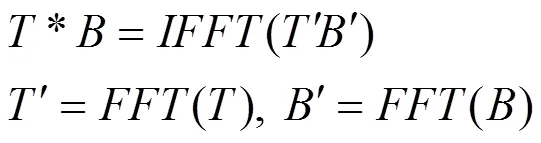
式中:*号代表卷积运算,FFT和IFFT分别代表正反快速傅里叶变换。计算基准图每个窗口与模板图像之间的相关,即是计算基准图与模板图像之间的卷积。假设基准图的特征分量图为²,模板图的特征分量图为TN²,则可以按下列公式计算8个特征分量的卷积和,即是计算模板图与基准图所有窗口的相似性:
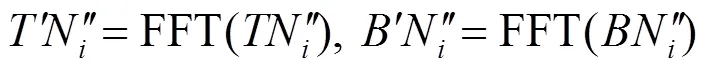
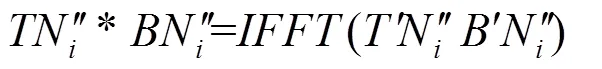
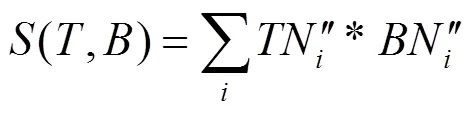
基于FFT的卷积计算的复杂性为:
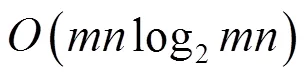
表1将空域匹配计算(按照公式(6))与频域匹配计算(按照公式(9)~(11))进行了比较。可见利用FFT优化的频域匹配能大幅提升计算速度。
3 测试比较及计算性能分析
3.1 测试比较
本文匹配算法与以下4种异源图像匹配算法进行了比较,包括:
1) PQ-HOG(histogram of orientated gradient, HOG)[10]:该方法是一种基于图像结构特征的匹配算法。该算法先逐像素提取梯度直方图,然后将HOG通过投影矩阵二值化,再利用海明(Hamming)距离计算相似性。
2) HOPC(histogram of orientated phase congruency, HOPC)[12]:该方法也是一种基于图像结构特征的匹配算法。该算法先逐像素提取相位一致性方向直方图,然后使用归一化互相关(NCC)计算相似性。
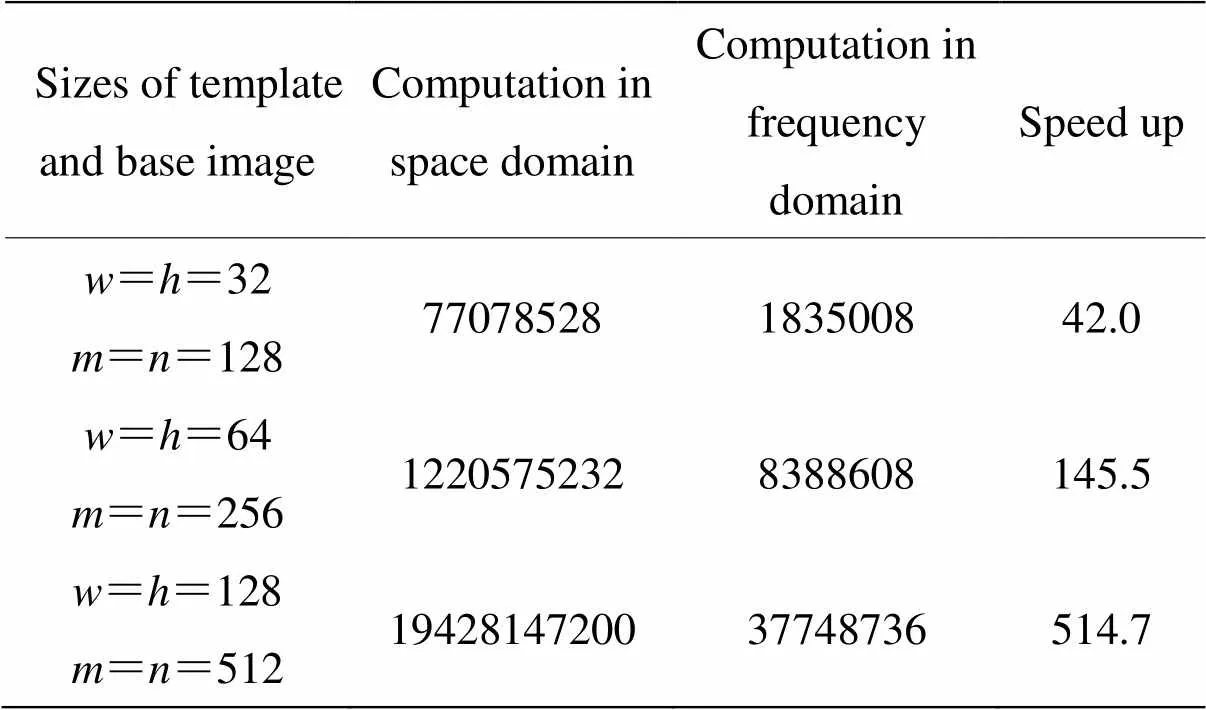
表1 比较空域匹配计算和频域匹配计算
3) MTM[4]和MI[6]:这两种方法都是直接基于图像灰度的匹配算法。MTM算法能够适应满足函数映射关系的非线性灰度畸变,MI算法能够适应满足非函数映射关系的非线性灰度畸变。
本文使用了地图、红外、可见光和SAR图像作为测试数据,图3给出了3组测试图像示例。
比较测试结果如图4(a)所示,可见随着模板图尺寸增加,算法的匹配错误率都在降低。基于特征的3种匹配算法普遍优于直接基于灰度的两种匹配算法。两种灰度算法中,MI的匹配错误率更低,平均低3.67%。3种基于特征的匹配算法中,本文算法(proposed algorithm, PA)和HOPC算法要优于PQ-HOG。HOPC在模板尺寸为32×32和64×64时,匹配错误率比本文算法低,而在模板尺寸为96×96,128×128时,匹配错误率比本文算法高。本文算法的平均误匹配率为30.45%,为5种测试算法中最低。图4(b)给出了比较算法在添加高斯噪声干扰图像上的测试结果,图5给出了对测试图像增加不同级别高斯噪声的例子。噪声图像匹配测试结果显示,随着噪声增强,算法匹配的错误率,都在增加,整体上,本文算法的匹配结果优于其它算法,说明本文算法对噪声有较好的适应能力。
本文算法可以有效实现红外、可见光、以及SAR图像之间的匹配,图6给出了本文算法的匹配结果示例。
3.2 计算性能分析
本节对PQ-HOG、HOPC、MI、MTM和本文算法的计算时间进行了测试,实验机CPU为Intel core i5-4300U 2.50GHz。表2给出了5种算法对不同尺寸模板和基准图像匹配的计算时间。其中MTM和本文算法都是通过频域卷积实现匹配。这两种算法的计算速度明显快于其他3种算法。本文算法计算速度略快于MTM,是5种算法中计算速度最快的算法。MI则是5种算法中计算速度最慢的算法。
图7给出了本文算法使用空域匹配和使用频域匹配计算时间的比较。对给定大小的搜索空间,空域匹配的计算时间随模板尺寸成指数级增长。而频域匹配的计算时间主要由基准图大小决定,因此基本不随模板尺寸变化而变化。

图3 异源图像对示例
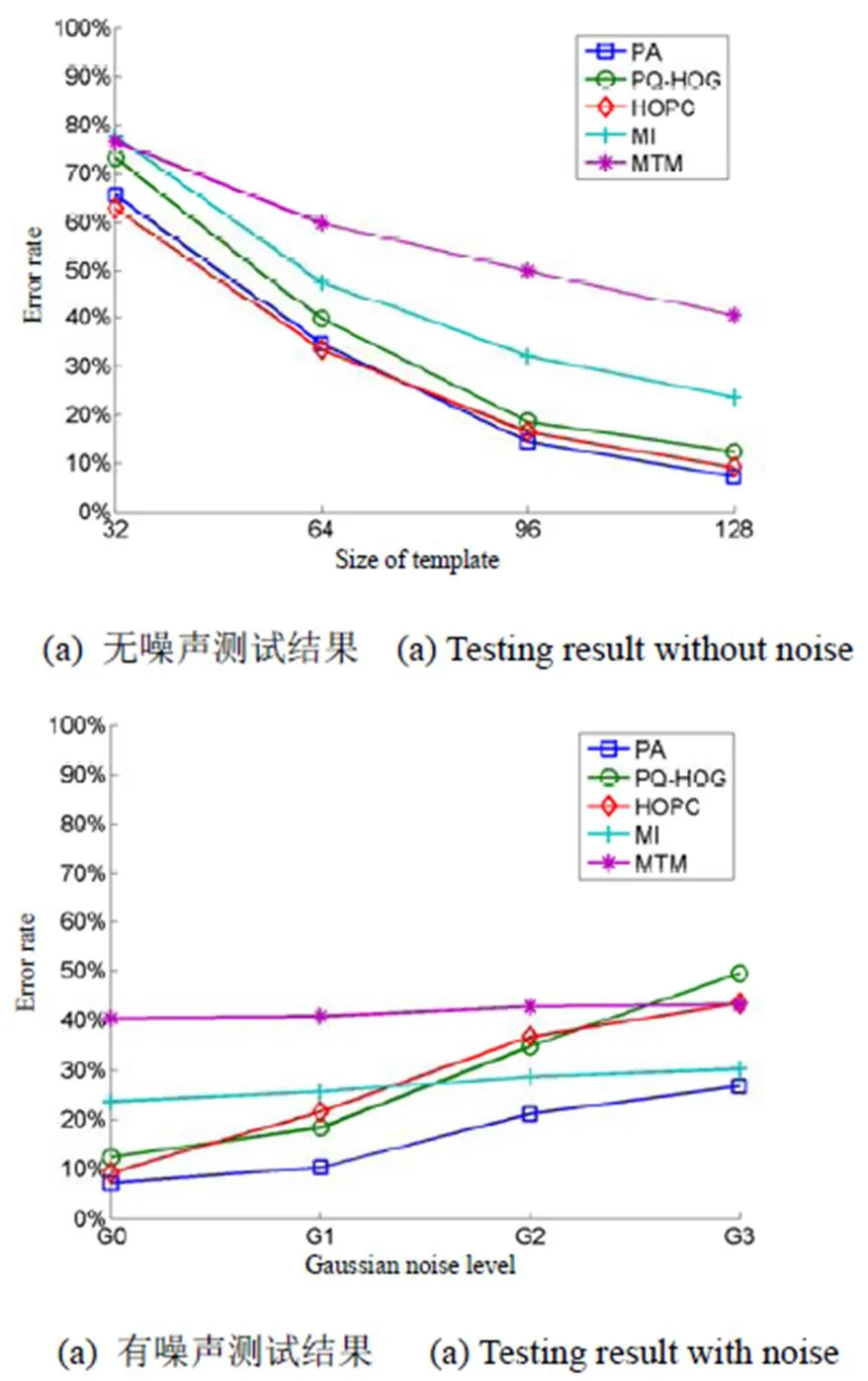
图4 异源图像匹配算法测试结果

图5 原图像和增加了噪声的图像

