利用正弦幅值时间转换的脉冲激光测距方法

黄民双，关在辉，姜 博

利用正弦幅值时间转换的脉冲激光测距方法

黄民双，关在辉，姜 博

（北京石油化工学院 光机电装备技术北京市重点实验室，北京 102617）

提出了一种利用正弦幅值时间转换的高精度脉冲激光测距方法，该方法以正弦信号作为时间基准，采用倍频和时钟分相技术，通过调节脉冲发射延时，控制回波脉冲定时点落在基准正弦波的0～p/4区间，然后对这一区间进行分段线性插值处理，将正弦幅值的变化转换为定时时间，实现高精度测距。该方法原理结构简单、容易实现。实验结果表明：在激光发射平均功率为1mW时，在无合作目标测程300m内，测距精度为±(5mm＋3ppm)。

激光测距；脉冲飞行时间；正弦基准；幅值时间转换；定时误差

0 引言

脉冲激光测距仪在工业、测绘、军事上有重要的应用[1]，它是基于脉冲飞行时间（Time of Flight，TOF）技术，TOF是指从测距仪发射的激光脉冲经目标返回探测器的传输时间，即所谓的脉冲飞行时间，TOF的测量精度直接影响测距精度。

现有脉冲激光测距仪是采用粗测和精测相结合的方法，在脉冲飞行时间内，对高频时钟周期进行计数，得到粗测值，然后再对不足一个高频时钟周期的部分进行内插处理，以获得精测值。内插精度决定了时间测量精度，传统的内插法主要有数字内插法和模拟内插法。数字内插法是利用门电路的传输延时或延时差原理，如数字延迟线法、数字锁相环法、数字游标法等，但精度受到电路器件延时分散性和电路温度漂移的影响，时间测量误差在100ps以上，对应的测距精度为15mm（当高频时钟频率为15MHz时）。模拟内插法是用恒流源对一个电容器进行充电或放电，通过测量电容上电压幅值变化来计算时间间隔，也称为幅值时间转换法，在很短的测程内理论精度可以达到几皮秒，但存在电容漏电和温度漂移的影响，在100ns时间内变化约10～30ps/℃[2]，为了解决温漂问题，通常利用CMOS技术将时间测量模块制作成集成电路[3-7]，在几微秒的测量范围内预期精度可达10ps[8]，但是这种高精度的时间测量芯片价格昂贵，特别是这种电容器充放电的方法还存在时间测量盲区，无法应用于脉冲激光测距仪中。

本文的目的是设计一种测程数百米、精度毫米级的低成本测距仪，其技术方案以正弦波为时间测量基准，利用基于共振探测定时方法[9]，通过调节脉冲发射延时，控制回波脉冲定时点落在高频时钟正弦波的0～p/4区间，然后利用这一区间进行分段线性内插处理，实现毫米级的高精度测距。

1 测距原理

1.1 技术方案

为了实现高精度远目标测距，测距系统采用粗测和精测相结合的技术方案，本文采用正弦信号作为高频时钟[10]，因为正弦波最容易在电路中产生，该时钟信号既作为控制激光脉冲发射的信号，又作为时间间隔测量基准，这比传统的采用直线[3]（由电容充放电产生）作为时间间隔测量基准的方法容易实现，并且不存在时间测量盲区问题。如图1所示，设高频时钟周期为0，脉冲发射时刻为高频时钟过零时刻star，返回的时刻为stop点，则由光在空气中的光速可计算出从测距仪到目标之间的距离为：

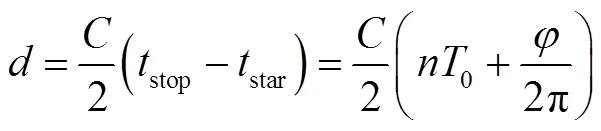
式中：0表示高频时钟的整周期个数，即粗测值，可以通过传统的脉冲计数方法测得；而相位取值范围为∈[0, 2p)，为不足一个周期的相位值，即精测值，的测量精度决定测距精度，因此本文的关键问题是如何提高相位的测量精度。

1.2 幅值时间转换

正弦波是非线性的，在最大值（p/2处）或最小值（3p/2处）附近幅值变化率很小，这就意味着在这些区域内很小的幅值变化将对应较大的相位变化。假设距离分辨率为1mm，则需要对一个正弦周期进行10000倍相位细分（设高频时钟频率为15MHz），可求出最小幅值分辨率为1.974×10－5。但是，这一微小的幅值变化是无法分辨的，因为电路中正弦波幅值噪声将远大于这个最小幅值分辨率。

为此，本文提出利用0～p/4区间这一近似线性段作为定时特征点，在这一区间正弦幅值的变化率较大，这样就避免了在p/4～p/2区间正弦幅值变化率小导致的相位细分困难。如图2所示，通常脉冲发射时刻设置在高频正弦波的0点，其回波脉冲定时点对应正弦波相位在∈[0, 2p)的范围。为了使回波脉冲定时点落在∈[0,p/4)区间，可以通过控制脉冲发射延时来实现。具体方法是：先将高频正弦波进行4倍频，然后再利用高频时钟的上升沿0点和下降沿p点进行二分相处理，这样就将高频时钟周期划分为8个分相区间，相邻分相区间为p/4（如图2）。将测量过程分为两个步骤：

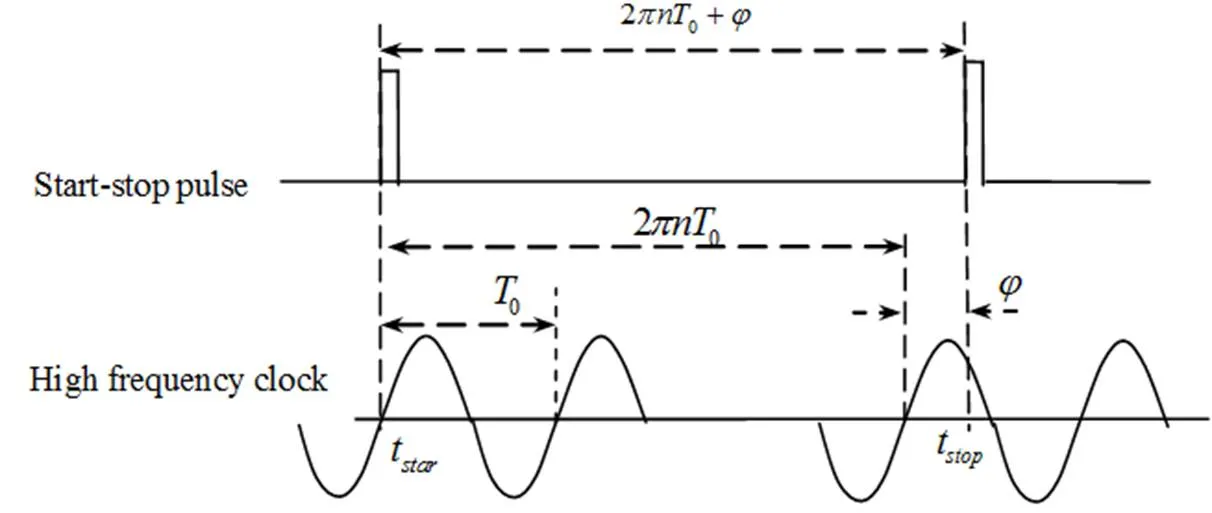
图1 利用正弦基准的激光测距原理

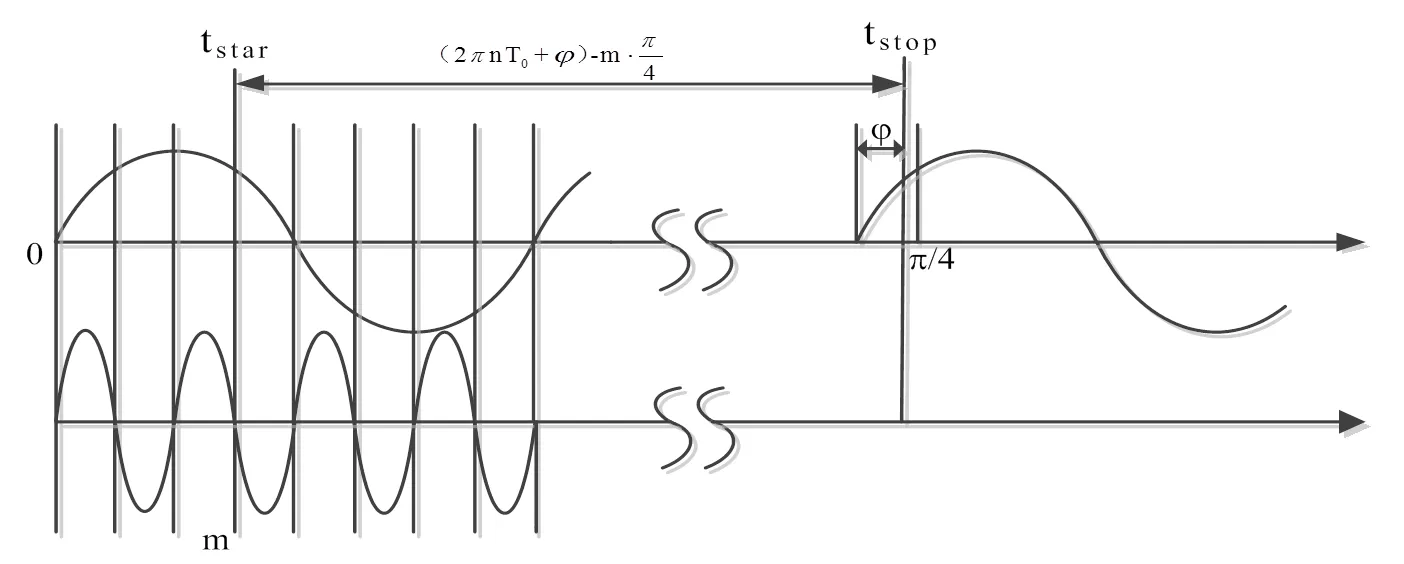
图2 利用正弦波0～p/4区间的幅值时间转换原理

1）在正弦波0点发射脉冲，估算相位所在的分相区间，确定延时区间数。

2）在延时区间点发射脉冲，其距离为：

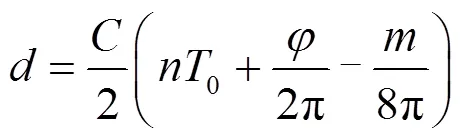
式中：∈[0,p/4)。采用倍频和分相技术会引起时间偏移（Skew）和抖动（Jitters），时间偏移为系统误差，可以用高精度测距仪来校正；而时间抖动属于随机误差，可以通过多次测量取平均来减小或消除。

1.3 测量精度的提高

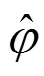
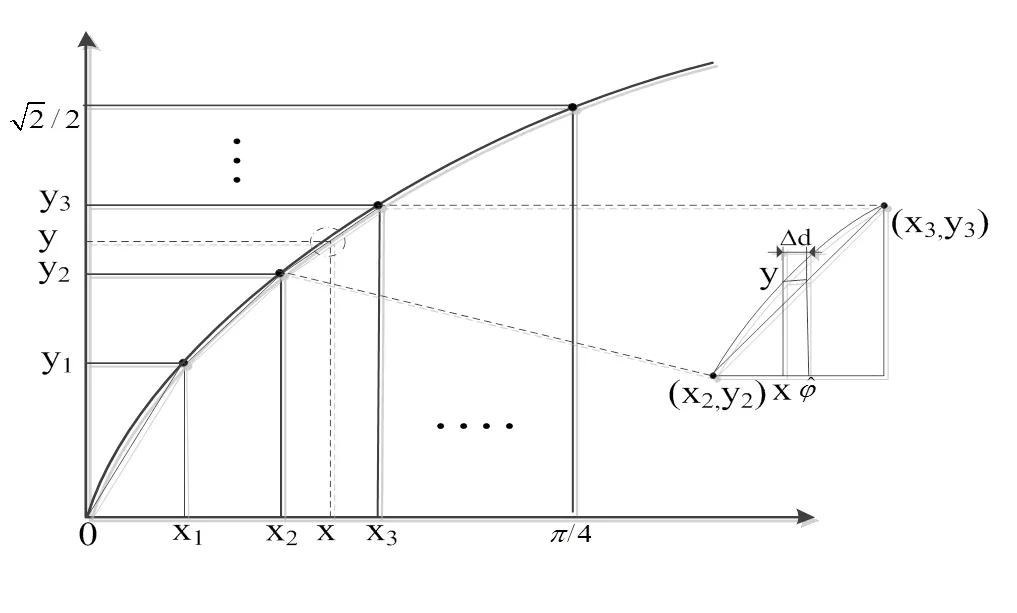
图3 分段线性内插示意图

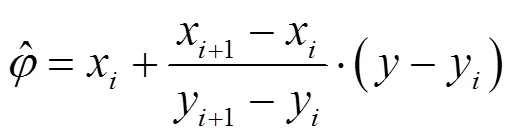
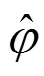
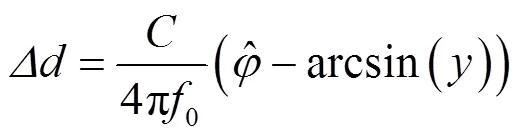
图4为分别取＝10, 20, 50时的原理误差曲线，其中横坐标为0～p/4的相位，纵坐标为线性插值误差D，图5是给出了最大原理误差Dmax随的变化关系，Dmax是指在0～p/4区间的最大线性插值误差，从图4可以看出越大，原理误差D越小，如果取＝20，则Dmax＜0.3mm，对于毫米级测距精度来说，线性插值产生的原理误差可以忽略。

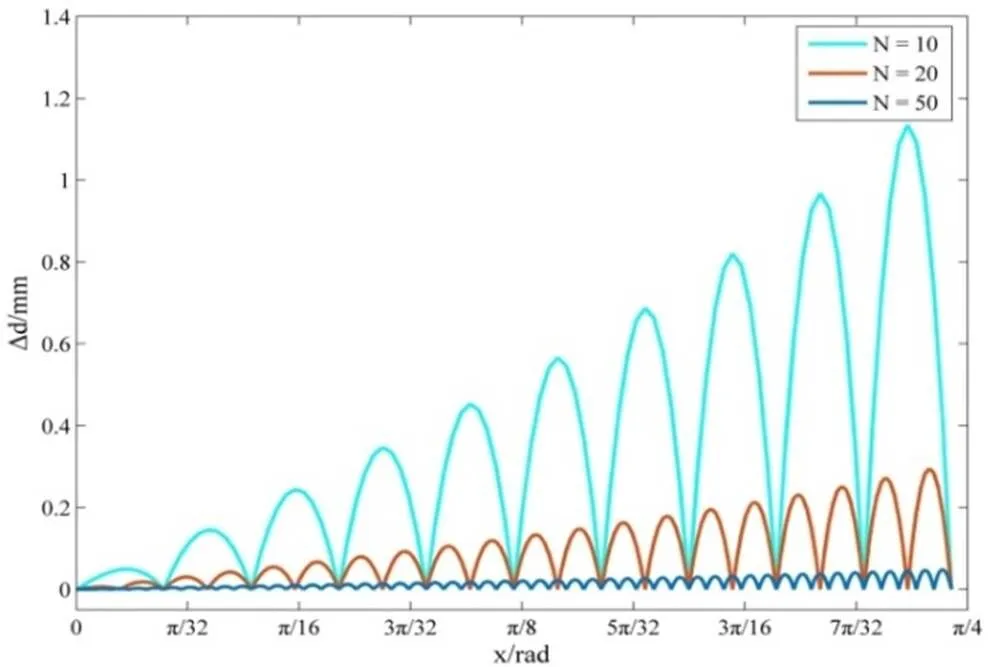
图4 在0～p/4区间线性插值原理误差

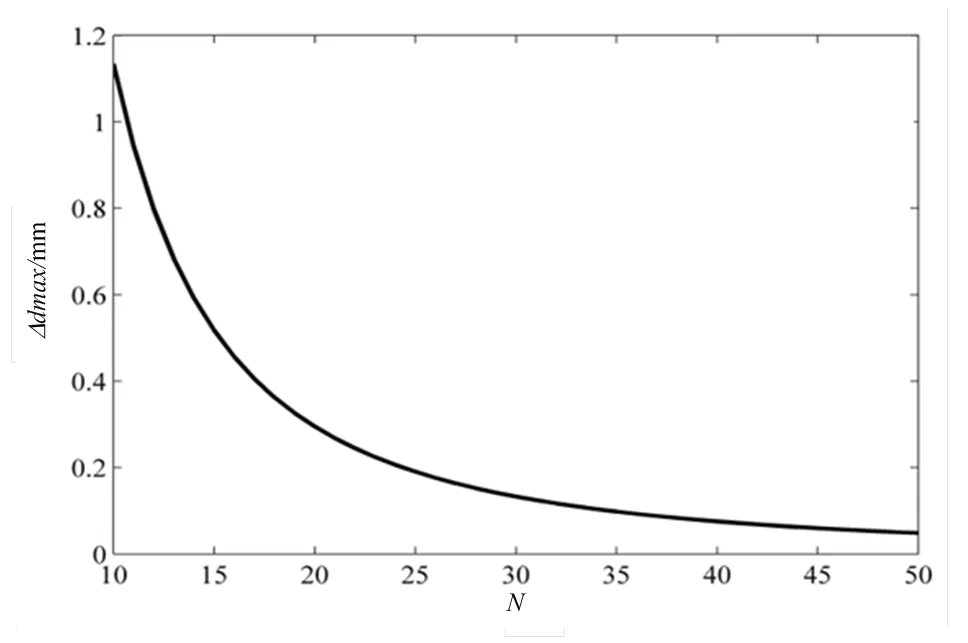
图5 最大线性插值原理误差随N变化关系

本方案中，采用共振探测定时方法基本上消除了走离误差，其残余误差可以视为均值为零的随机误差，利用多脉冲的测量结果取平均，预期可以实现毫米级的测量精度。

2 测距系统

激光测距系统框图如图6所示。测量系统主要由脉冲激光发射、光电转换、时刻鉴别、数据采集处理以及控制等部分组成。晶振选用温度补偿晶体振荡器，频率为15MHz，频率稳定度为±0.1ppm（－30℃～＋85℃）；半导体激光二极管波长为870nm，峰值功率10W，脉宽5～10ns，最高脉冲发射重复频率大于100kHz；光电探测器（Avalanche Photo Diode，APD）中心波长800nm，响应度50A/W；AD转换器为12位，最大转换速率5Msps。晶振输出信号转换为方波和正弦波，分别作为脉冲激光发射时刻控制信号和正弦基准时钟信号，脉冲激光经目标漫反射，由光电探测器APD转换为脉冲光电流，然后经时刻甄别后产生定时信号，以此定时信号触发采样器ADC采样正弦量化时钟信号，最后经单片机处理后输出距离信息。

在光路上设置了内外光路，其目的是消除由温度漂移产生的时间间隔误差，脉冲在发射通道和接收通道中传输的时间受电路温度漂移的影响是很大的，经实验测量最大可达到约26.8ns的时间漂移，相当于4m距离误差。在电路上设置一个共用的接收通道，如果分别设置内光路和外光路接收通道，由温度漂移导致的稳定偏差2mm/℃，相当于14ps/℃，如果共用一个接收通道，则稳定性提高到0.1mm/℃[11]。

设置减光板是为了控制脉冲光电流幅值的变化和消除走离误差的影响[9]，回波脉冲光强与目标物体表面几何形状、光学特性以及目标距离有关，回波光脉冲幅值最大变化范围将达到1:100000，将造成电路检测的困难，因此采用减光板控制脉冲光电流在一定的变化范围内，以满足高精度远目标测距的要求。

根据上述系统总体结构，设计出了脉冲测距的电路硬件系统和软件系统，并结合已有光学和机械等部分，最终搭建了脉冲激光测距装置系统，如图7所示，系统主要包括光路部分、硬件电路、示波器、电源、RS232通讯接口和上位机几个部分。由于光路器件对外界环境要求较高，因此都集成安装在测距头里；示波器为美国Agilent公司生产的54642A型号，带宽为500MHz，采样率为2GSa/s，

与硬件电路连接，可以随时观察回波信号的变化以及各部分电路的输出波形；硬件电路安装在测距头的上方，控制整个测距系统的工作和运行；上位机通过RS232协议接口与测距仪的硬件部分连接，完成数据的通讯和测量结果的显示。

3 实验结果

为了验证在∈[0,p/4)区间正弦幅值时间转换的可行性，将该区间分为20等分，即取＝20，图8为在固定目标距离下外光路测量误差，测量次数为100，测量误差为单发脉冲的测量值与100次测量的平均值之差。从图8可以看出，单发脉冲误差为±50mm，这表明在测量数据上叠加较强的噪声，换言之，测量数据已经被噪声严重污染。但是，从图8可以看出单发脉冲误差是随机的，因此可以利用连续多脉冲的测量结果进行平均处理来减小。假设误差分布服从均值为零、方差为2的正态分布，由于采用半导体激光二极管光源，其脉冲重复频率最高可达100kHz，在40ms测量时间内发射＝400个脉冲，预期测距精度能够提高到2/＝1mm。但是，发射电路、目标特性、探测电路等都对定时误差有贡献，这些因素产生的时间抖动还会包含未知的、可变的系统误差或周期误差[12]，另外正弦基准信号是采用简单的RC滤波器得到，电路或器件的非线性将导致正弦波发生畸变，最终也会对测距误差有贡献。

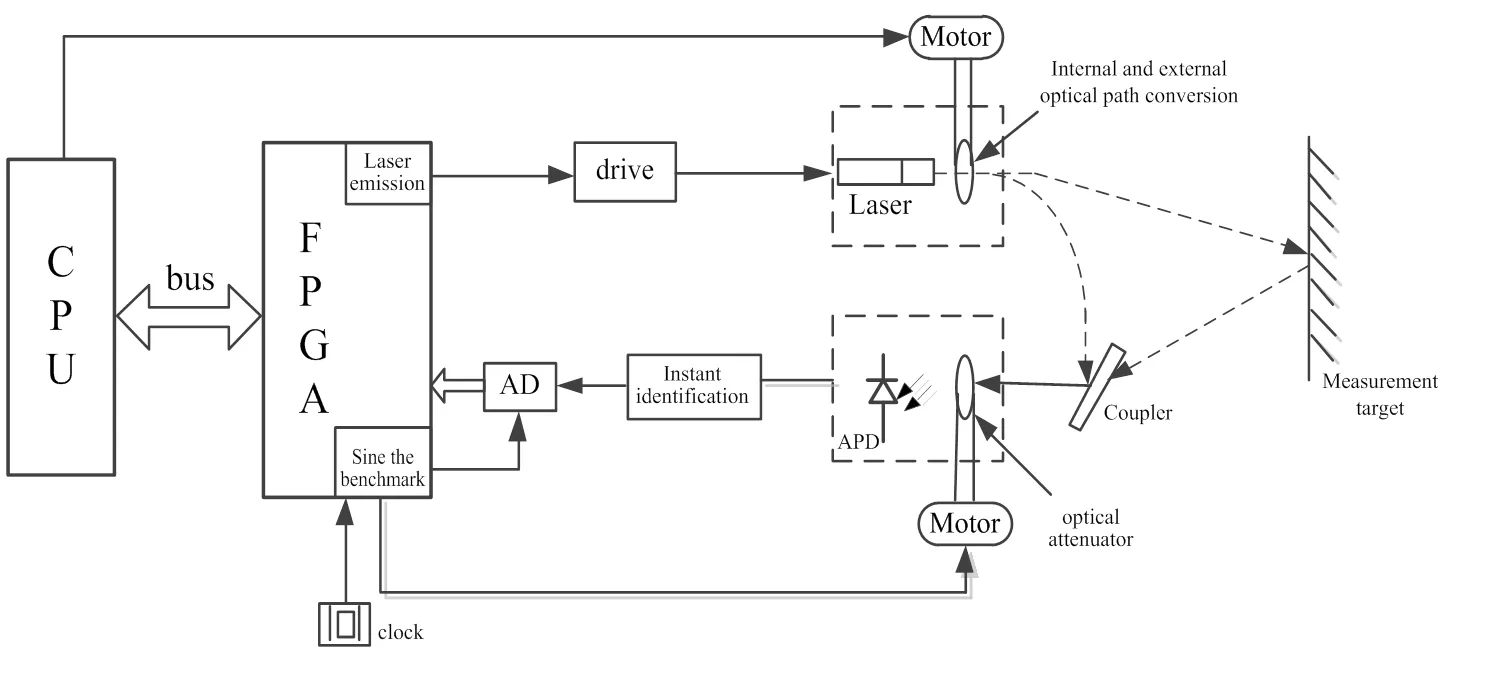
图6 激光测距系统总体框图

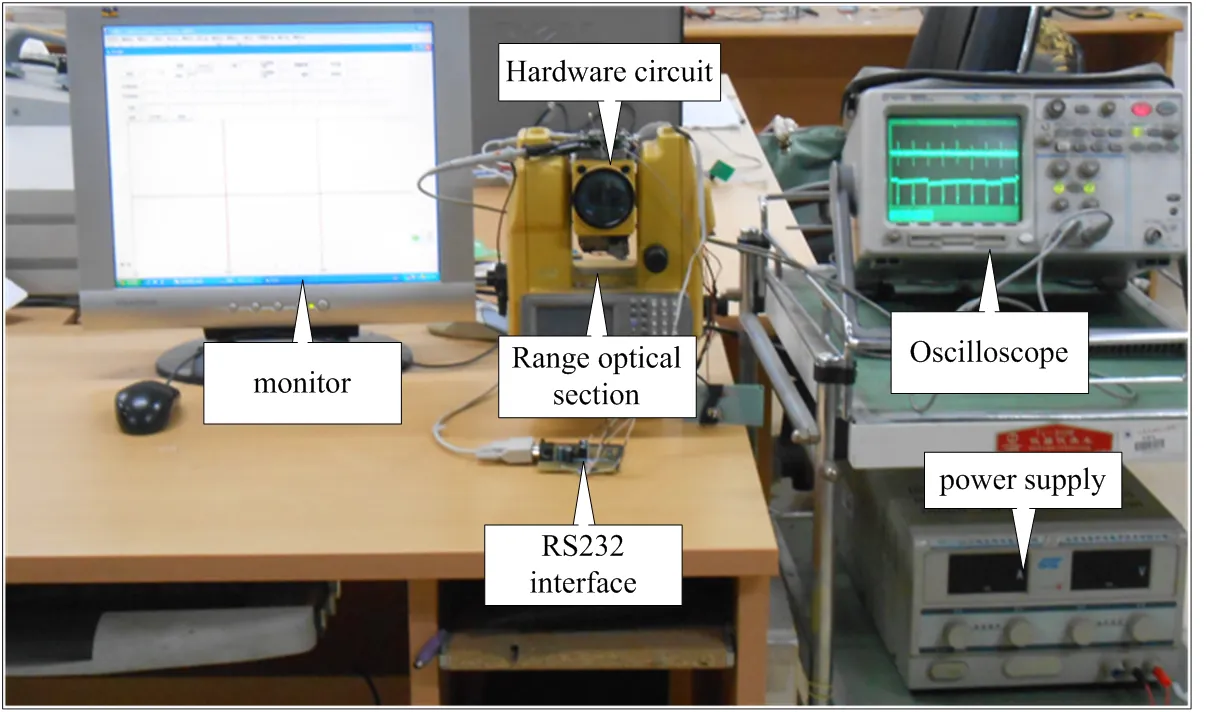
图7 测量系统实物图

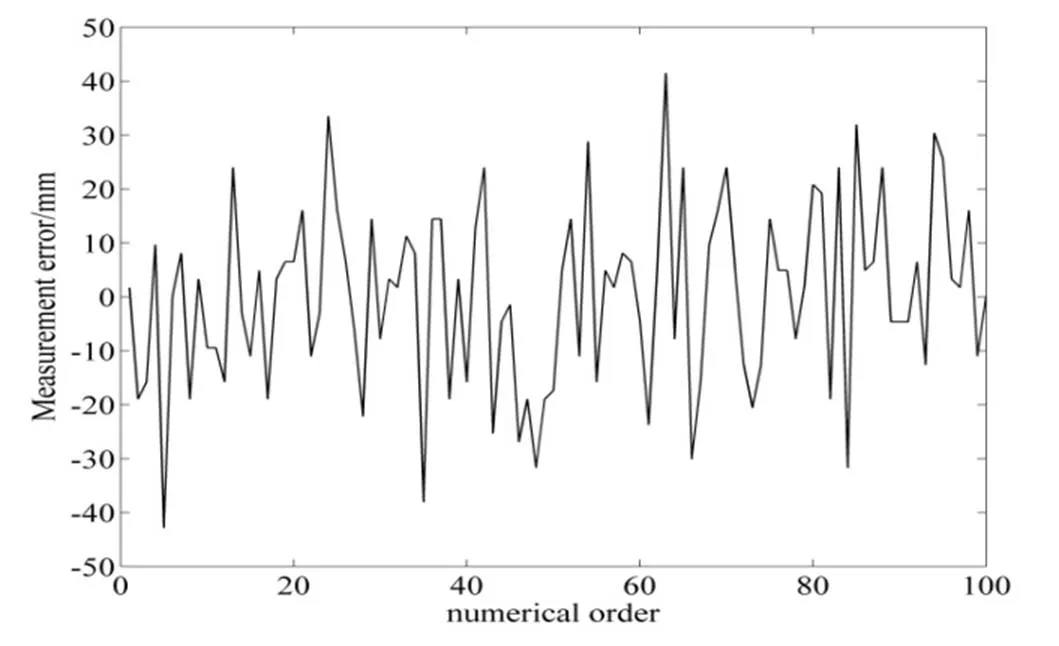
图8 固定目标距离下外光路测量误差

将研制的测距系统装配在全站仪上，与精度±(3mm＋2ppm)的测距仪进行对比测试，其测距误差如图9所示，这个误差为标准偏差，即对目标点测量10次计算标准偏差，然后以最大标准偏差作为评价指标，从图9可以看出，在无合作目标35m测程内，距离误差仅在±2.5mm内。经过测试，在300m的测程内，测距系统测距精度±(5mm＋3ppm)。说明本文所提出的脉冲激光测距技术方案是可行的。

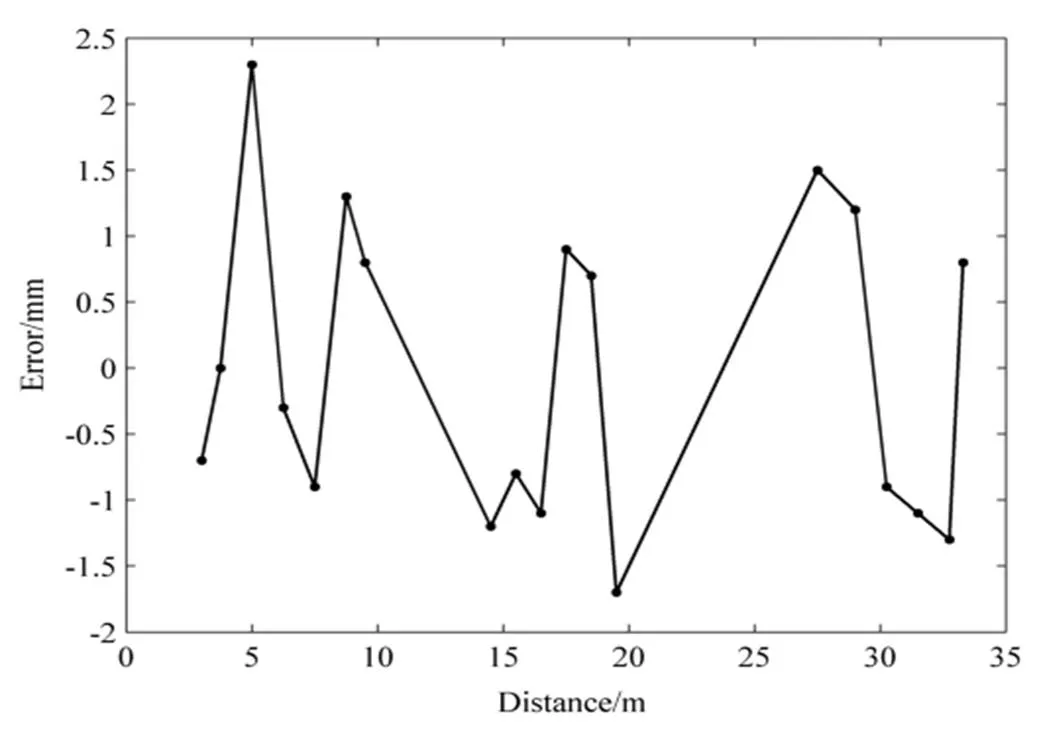
图9 在1.5～35m内不同目标距离的误差测量曲线

4 结论

本文研究一种基于正弦波幅值时间转换的高精度激光测距方法，其原理是通过控制脉冲发射延时，以0～p/4区间的值作为定时特征点，对这一区间进行分段线性插值处理，实现高精度测距，测距精度达到±(5mm＋3ppm)，可用于大型工程结构（如公路、桥梁）、建筑结构、工业现场等方面测量。该方法采用正弦信号作为量化时钟，该信号同时作为激光脉冲发射控制信号和时间间隔测量基准，与传统的利用电容充放电的幅值时间转换方法相比，电路结构简单、容易实现，并且不存在时间测量盲区问题。今后的工作需要解决定时误差影响或正弦基准信号畸变的问题，进一步提高精度。

[1] 黄民双. 单发脉冲飞行时间激光测距技术[J]. 激光与光电子学进展, 2017, 54(12): 63-69. HUANG M S. Time-of-flight laser ranging technique of single transmitted pulse[J]., 2017, 54(12): 63-69.

[2] Sasaki O, Taniguchi T, Ohska T, et al. A high resolution TDC in TKO BOX system[J]., 1988, 35(1): 342-345.

[3] Ilkka Nissinen, Juha Kostamovaara. On-Chip Voltage Reference-Based Time-to-Digital Converter for Pulsed Time-of-Flight Laser Radar Measurements[J]., 2009, 58(6): 1938-1948.

[4] Kurtti S, Kostamovaara J. An Integrated Laser Radar Receiver Channel Utilizing a Time-Domain Walk Error Compensation Scheme[J]., 2011, 60(1): 146-157.

[5] Cho H S, Kim C H, Lee S G. A High-Sensitivity and Low-Walk Error LADAR Receiver for Military Application[J]., 2014, 61(10): 3007-3015.

[6] Nissinen J, Nissinen I, Kostamovaara J. Integrated Receiver Including Both Receiver Channel and TDC for a Pulsed Time-of-Flight Laser Rangefinder With cm-Level Accuracy[J]., 2009, 44(5): 1486-1497.

[7] Maatta K, Kostamovaara J, Myllyla R. Profiling of hot surfaces by pulsed time-of-flight laser range finder techniques[J]., 1993, 32(27): 5334-5347.

[8] Jansson J, Mäntyniemi A, Kostamovaara J. A CMOS time-to-digital converter with betterthan10ps single-shot precision[J]., 2006,41(6): 1286-1296.

[9] 黄民双, 马鹏, 刘晓晨. 高频共振预探测多脉冲激光测距方法[J]. 物理学报, 2018, 67(7): 074202-1-074202-10。 HUANG M S, MA P, LIU X C. Multi-pulse laser ranging method for pre-detection with high frequency resonance[J]., 2018, 67(7): 074202-1-074202-10.

[10] 黄民双, 龙腾宇, 刘慧慧, 等. 基于正弦曲线的高精度脉冲激光测距时间间隔测量技术[J]. 中国激光, 2014, 41(8): 0808002-1-0808002-6. HUANG M S, LONG T Y, LIU H H, et al. A high-precision pulsed laser ranging time interval measurement technology based on sine curves method[J]., 2014, 41(8): 0808002-1- 0808002-6.

[11] Maatta K, Kostamovaara J. A High-Precision Time-to-Digital Converter for Pulsed Time-of-Flight Laser Radar Applications[J]., 1998, 47(2): 521-534.

[12] 黄民双, 刘晓晨, 马鹏. 脉冲飞行时间激光测距系统中周期误差补偿[J]. 红外与激光工程, 2018, 47(3): 0317004-1-0317004-5. HUANG M S, LIU X C, MA P. Periodic error compensation of pulsed time-of flight laser ranging system[J]., 2018, 47(3): 0317004-1-0317004-5.

Pulse Laser Ranging Using Sinusoidal Amplitude Time Conversion

HUANG Minshuang，GUAN Zaihui，JIANG Bo

(,,102617,)

In this study, a high-precision pulse laser ranging method, employing sinusoidal amplitude time conversion, is proposed. The method uses a sinusoidal signal as a time reference, and frequency doubling and the clock phase separation technique to control the echo pulse timing by adjusting the pulse emission delay. The signal falls within the 0-p/4 interval of the reference sine wave, and then effects piecewise linear interpolation for the given interval to convert the variation of the sinusoidal amplitude into the time required for achieving high-precision ranging. The underlying principle of the method is simple and easy to implement. The experimental results show that when the average power of laser emission is 1 mW, the range accuracy is ± (5mm + 3ppm) within 300m without a cooperation target.

laser ranging, pulse flight time, sinusoidal reference, amplitude time conversion, timing error

TN247

A

1001-8891(2020)05-0483-05

2019-08-16；

2020-05-04.

黄民双（1964-），男，博士，教授，主要从事光纤传感与智能结构、大地测量仪器等方面研究。E-mail: huangminhsuang@bipt.edu.cn。