北京地铁隧道地表横向沉降槽参数分析

吴锋波， 金 淮， 杨歧焱， 郑卫强

(1.河北地质大学勘查技术与工程学院， 河北 石家庄 050031； 2. 北京市轨道交通设计研究院有限公司， 北京 100068)

0 引言

伴随着我国城市地铁建设的迅猛发展，北京地铁已进入了网络化运营时代，大量新工程仍在积极建设中。地铁隧道工程建设一般采用矿山法或盾构法施工，其引发地层位移和上方地表的纵横向变形，横向形成“沉降槽”。地表沉降槽的研究方法主要包括经验公式法、解析计算法、模型试验法和数值模拟法等[1-7]，经验公式法是研究隧道开挖引起地表沉降的重要方法之一。

Peck 公式是预测隧道施工引发地表变形的重要经验公式[8]，具有模型简单、实用有效的特点，可以很好地指导施工。由于不同地区地质条件差异较大，经验公式具有一定的地区性[9]。M. P. O’Reilly等[10]统计了不同地层中盾构隧道的地层损失率取值范围；R. J. Mair等[11]给出了英国不同地层、不同开挖方法下隧道的地层损失率数值；S.Suwansawat等[12]研究了双线隧道开挖土体损失率与沉降槽宽度的取值。

GB 50911—2013《城市轨道交通工程监测技术规范》将Peck 公式作为土质隧道影响分区的重要依据，规定其影响范围一般包括主要影响区和次要影响区，主要影响区为隧道正上方及沉降曲线反弯点范围内，次要影响区为隧道沉降曲线反弯点至沉降曲线边缘2.5i处(i为沉降槽宽度)[13]。各地针对地铁隧道地表沉降槽的预测参数开展了相关研究，多基于一定数量的实测数据对Peck 公式的相关参数进行拟合分析。魏纲[14]统计分析了我国71 个盾构法隧道的土体损失率实测值；郭玉海[15]拟合得出了北京地铁14号线大直径土压平衡盾构的沉降槽参数；陈春来等[16]研究了双线水平平行盾构隧道施工中的土体损失；王鹏等[17]、段绍伟等[18]、蒋彪等[19]、麻凤海等[20]分别研究了武汉、长沙、长春等地的地铁隧道沉降槽参数；朱才辉等[21-22]整体分析了我国地铁沉降槽相关参数的变化规律；吴昌胜等[23]研究了我国不同直径盾构隧道的地层损失率情况；吴红博等[24]、丁智等[25]研究了双线地铁盾构隧道的地层变形特征及土体损失率取值。

相关研究取得了一定的成果，然而由于基础数据有限，沉降槽参数的统计分析结果在新建隧道工程地表变形预测方面有一定的局限性，不能准确地确定隧道工程的不同影响区域和影响范围。本文基于北京地铁丰富的沉降槽资料，针对某一城市开展全面、系统的沉降槽拟合参数的数理统计分析研究，相关成果可以很好地揭示其横向沉降槽的变形特性，以期为今后该地区或类似地层城市中隧道工程影响区域划分、影响范围确定等提供参考。

1 Peck 公式及相关预测参数

1969年美国R. B. Peck[8]借鉴采矿学中地面沉降位移的估算方法，在总结大量实测资料的基础上，提出地层损失的概念和估算隧道开挖地表沉降的方法——Peck公式，沉降槽横断面曲线图见图1。假定地层损失在整个隧道长度上均匀分布，隧道施工所产生的地表沉降横向分布近似为正态分布，则地表沉降公式为：

(1)

(2)

式(1)—(2)中：S(x)为隧道两侧横向上距隧道中心x处的地面沉降量，m；Smax为隧道中心处的最大沉降量，m；x为隧道两侧横向上距隧道中心的距离，m；i为沉降槽宽度，曲线反弯点距隧道中心的距离，m；Vl为隧道单位长度的地层损失，m3/m。

其中：

(3)

式中：H为隧道覆土厚度，m；R为隧道计算半径，m；Z0为隧道中心埋深，m；φ为隧道周围地层内摩擦角，(°)。地面沉降槽总宽度W≈2.5i。

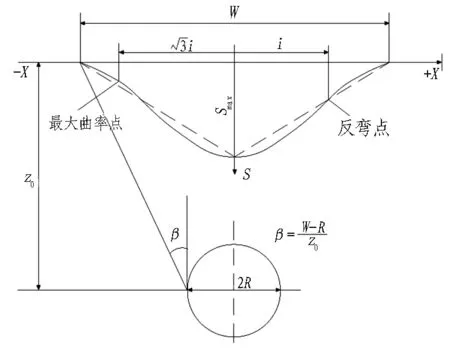
图1 沉降槽横断面曲线图

根据隧道工程地表横向变形形态和Peck公式可以看出，隧道地表横向变形数值与地层损失率Vl、沉降槽宽度i密切相关。已有研究表明，隧道地表沉降槽地层损失率Vl决定了沉降量的大小，沉降槽宽度i决定了沉降槽曲线的形状(如宽而浅或窄而深)。为更简单地描述沉降槽宽度，一般取沉降槽宽度系数k=i/Z0[9]。

以Peck公式为基础，对统计的实测数据进行线性回归，具体拟合方法见文献[26]，典型工程拟合结果见图2。

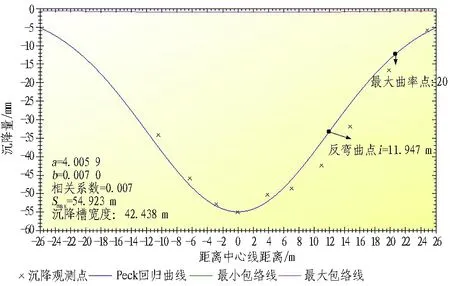
图2 典型工程拟合结果(5号线某车站)

本文主要选取地表沉降槽的最大沉降值拟合参数作为统计分析的基础数据，以合理预测隧道工程地表的最大变形和影响范围。

2 资料收集及分析

本研究采用监测单位资料收集、期刊文献整理摘录、相关书籍资料摘录等方式对我国北京地区地铁隧道工程地表横向变形资料进行全面、系统的收集，共收集到约13条地铁线路、903份隧道工程地表横向沉降槽资料。具体资料收集结果见表1和图3(图3中地铁线路加粗部分为资料包含的车站和区间)。

表1 沉降槽资料收集情况

注： 主要参考文献[27-33]。

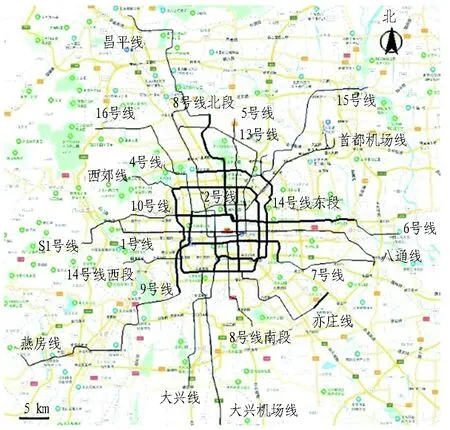
图3沉降槽资料范围示意图

Fig. 3 Scope diagram of settlement groove data

根据地铁隧道工程建设特点，将其分为车站、标准断面双线区间、大断面单线区间分别进行研究。双线区间隧道一般为左右线2条标准断面隧道，断面为马蹄形或圆形，直径在6 m左右。单线区间一般为大断面隧道，直径在10 m及以上。

根据隧道施工方法，分为盾构法和矿山法2类进行研究。根据北京地区地层特点，将隧道穿越地层分为黏性土地层(粉土、黏性土为主，一般位于城市中东部)和砂卵石地层(砂土、圆砾、卵石为主，一般位于城市中西部)2类进行研究[34-38]。

3 地铁车站地表横向变形特性

北京地铁车站的修建方法主要为矿山法，车站开挖区域内的地层主要为黏性土地层和砂卵石地层。

3.1 沉降槽最大沉降值

地表沉降槽的最大沉降值统计结果见图4。

由统计结果可知： 黏性土地层开挖的63个地表沉降槽中沉降最大值为166.60 mm，最小值为16.27 mm，平均值为79.57 mm，标准差为39.28 mm；最大沉降值分布形态近似为正态分布(图4中拟合曲线为正态分布曲线，下同)，其主要分布在40～60 mm区段；偏态系数SK=0.505，为中等右偏分布；峰态系数K=-0.665，为扁平分布。

砂卵石地层开挖的32个地表沉降槽中沉降最大值为148.14 mm，最小值为11.84 mm，平均值为61.01 mm，标准差为34.45 mm；分布形态近似为正态分布，最大沉降值主要分布在20～60 mm；偏态系数SK=0.530，为中等右偏分布；峰态系数K=-0.354，为扁平分布。

(a) 黏性土地层

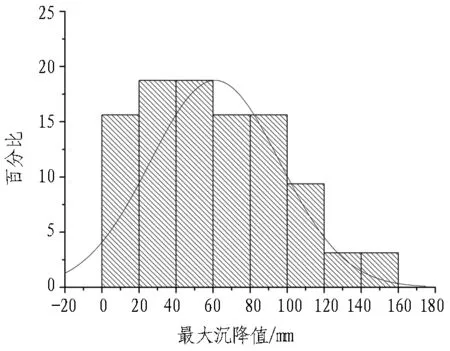
(b) 砂卵石地层

地铁车站开挖断面较大，埋深一般较浅，受地层条件影响较大，同时，对车站上方城市道路交通、地下管线也有一定影响，供水、雨污水等地下管线的渗漏引发的地层空洞致使车站上方地表变形不易控制。由于大粒径卵石的自稳性相对较好，砂卵石地层变形相对小一些。矿山法车站施工应注意地层条件和环境条件的影响，加强对地层变形的控制。

3.2 地层损失率

地表沉降槽的地层损失率统计结果见图5。

由统计结果可知： 剔除5个拟合异常值后，黏性土地层开挖的32个地表沉降槽中地层损失率数值最大值为6.90%，最小值为0.40%，平均值为1.85%，标准差为1.92%，中位数为1.00%；其分布形态近似为半正态分布，数值主要分布在0%～1.5%，约占总数量的78.1%。

砂卵石地层开挖的26个地表沉降槽中地层损失率数值最大值为3.75%，最小值为0.40%，平均值为1.41%，标准差为0.88%，中位数为1.35%；分布形态近似为正态分布，数值主要分布在1.0%～1.5%，约占总数量的50.0%；偏态系数SK=1.712，为高度右偏分布；峰态系数K=2.172，为尖峰分布;砂卵石地层具有一定的自稳性，对地层变形影响较大，隧道开挖的地层损失率数值相对较小。

(a) 黏性土地层

(b) 砂卵石地层

3.3 宽度参数

地表沉降槽的宽度参数统计结果见图6。

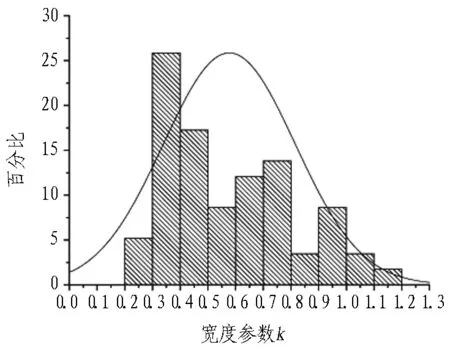
(a) 黏性土地层

(b) 砂卵石地层

由统计结果可知: 黏性土地层中开挖的58个地表沉降槽宽度参数最大值为1.18，最小值为0.22，平均值为0.58，标准差为0.24，中位数为0.54；近似为正态分布，主要分布在0.3～0.4；偏态系数SK=0.648，为中等右偏分布；峰态系数K=-0.463，为扁平分布。

砂卵石地层中开挖的30个地表沉降槽宽度参数最大值为1.00，最小值为0.46，平均值为0.67，标准差为0.14，中位数为0.63；近似为正态分布，数值主要分布在0.6～0.7；偏态系数SK=1.175，为高度右偏分布；峰态系数K=0.826，为尖峰分布。

3.4 相关性分析

地层损失率和宽度参数与隧道相对埋深(隧道中心轴线埋深/隧道直径或等效直径，下同)的相关性统计结果见图7。

(a) 地层损失率(黏性土)

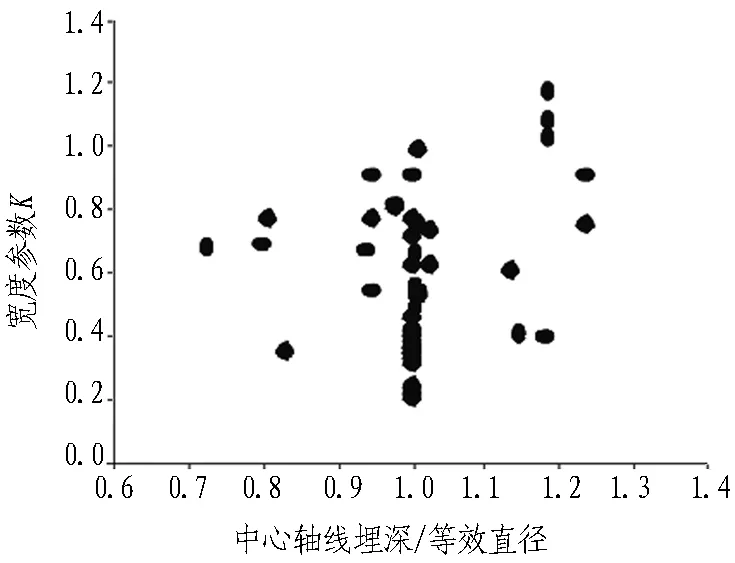
(b) 宽度参数(黏性土)

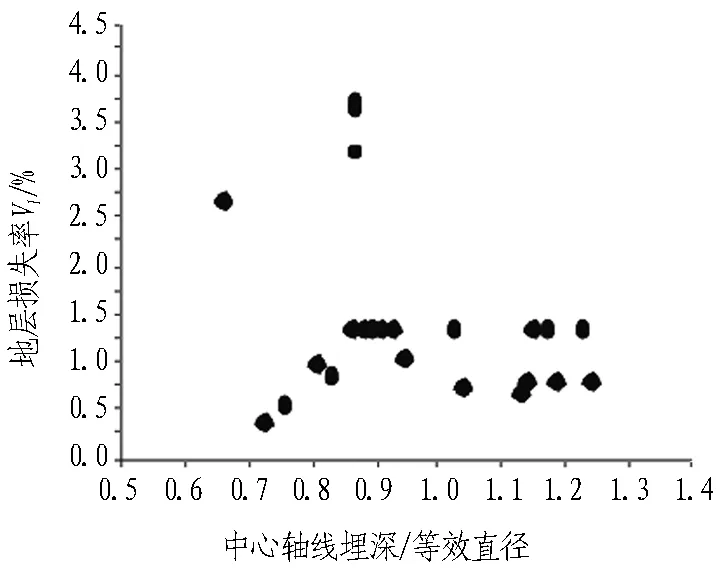
(c) 地层损失率(砂卵石)

(d) 宽度参数(砂卵石)

图7相关性分布图

Fig. 7 Relevance distribution

由统计结果可知： 隧道相对埋深的数值范围主要为0.6～1.3，黏性土地区沉降槽的地层损失率与宽度参数、砂卵石地区沉降槽的地层损失率等分布相对分散，随着隧道相对埋深的增加，没有明显的对应关系；砂卵石地区沉降槽的宽度参数随着该量纲一的量数值的增加近似有线性减小的趋势。

4 双线区间地表横向变形特性

北京地铁标准断面双线区间的修建方法主要为盾构法和矿山法，根据区间隧道开挖区域内的地层性质不同进行统计。双线隧道的沉降槽形态主要为双峰值型，沉降最大值一般出现在左右两隧道的中心轴线上方附近。左右线中心间距较大、2个沉降槽的形态较为完整时，分别进行拟合研究；左右线中心间距较小、2个沉降槽的形态不完整时，重点对变形值较大的沉降槽进行拟合研究。

4.1 盾构法施工隧道

4.1.1 沉降槽最大沉降值

地表沉降槽的最大沉降值统计结果见图8。

由统计结果可知，剔除由于涌水涌沙造成的3个地面沉降异常值，黏性土地层中盾构开挖的54个地表沉降槽中沉降最大值为32.60 mm，最小值为2.61 mm，平均值为11.39 mm，标准差为6.62 mm；近似为正态分布，主要分布在8～10 mm；偏态系数SK=1.245，为高度右偏分布；峰态系数K=1.552，为尖峰分布。

砂卵石地层中盾构法隧道的变形控制效果较好，19个地表沉降槽中沉降最大值为20.81 mm，最小值为2.99 mm，平均值为8.60 mm，标准差为4.58 mm；分布形态为多峰值分布，主要分布在4～6 mm和10～12 mm。

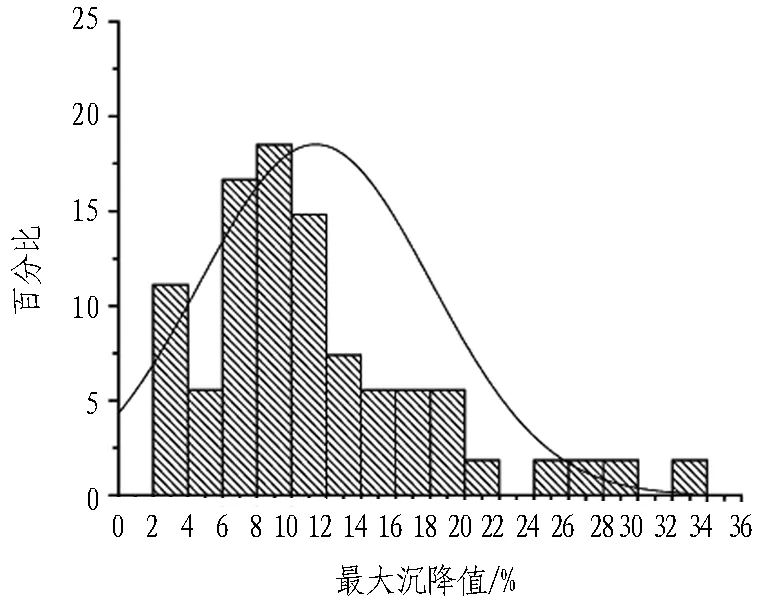
(a) 黏性土地层

(b) 砂卵石地层

4.1.2 地层损失率

地表沉降槽的地层损失率统计结果见图9。

(a) 黏性土地层

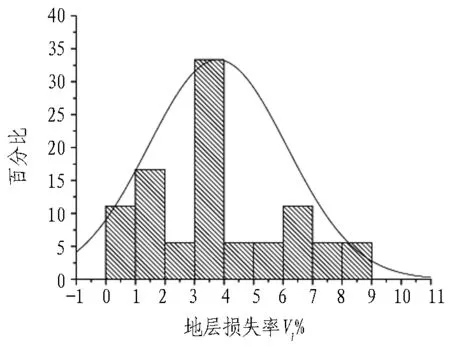
(b) 砂卵石地层

剔除7个拟合异常值后，黏性土地层盾构开挖的46个地表沉降槽中地层损失率最大值为8.40%，最小值为0.24%，平均值为3.80%，标准差为2.54%，中位数为3.73%；近似为多峰值分布，主要分布在0%～1%和3%～4%。

剔除5号线试验段的2个异常值后，砂卵石地层中盾构开挖的18个地表沉降槽地层损失率最大值为8.86%，最小值为0.51%，平均值为3.78%，标准差为2.28%，中位数为3.25%；近似为正态分布，主要分布在3%～4%;偏态系数SK=0.699，为中等右偏分布;峰态系数K=-0.158，为扁平分布。

双线盾构隧道施工过程中，先行隧道对周围地层具有扰动作用;后行隧道施工对周围地层形成二次扰动，造成地层损失率有一定的增加，出现了一些相对较大的数值，对地层损失率的整体分布形态有较大的影响。双线隧道的二次扰动效应与隧道埋深、隧道水平间距、地层特性、盾构施工参数(排土量和注浆压力等)等因素密切相关，施工过程中应予以重视，需深入开展相关研究。

4.1.3 宽度参数

地表沉降槽的宽度参数统计结果见图10。

(a) 黏性土地层

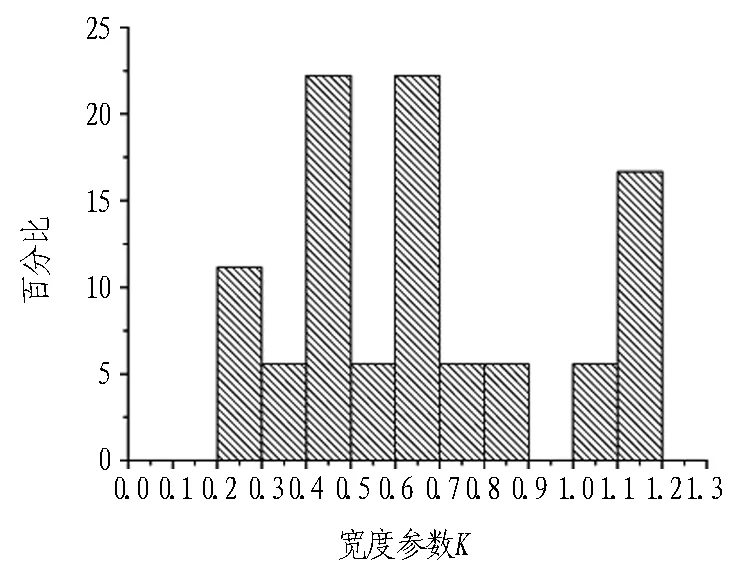
(b) 砂卵石地层

黏性土地层中盾构开挖的57个地表沉降槽宽度参数最大值为0.98，最小值为0.26，平均值为0.53，标准差为0.21，中位数为0.48；近似为正态分布，主要分布在0.3～0.4；偏态系数SK=0.880，为中等右偏分布；峰态系数K=-0.323，为扁平分布。

砂卵石地层中18个地表沉降槽宽度参数最大值为1.14，最小值为0.22，平均值为0.66，标准差为0.29，中位数为0.67；近似为多峰值分布，主要分布在0.4～0.5和0.6～0.7。

4.1.4 相关性分析

地层损失率和宽度参数与隧道相对埋深的相关性统计结果见图11。

(a) 地层损失率(黏性土)

(b) 宽度参数(黏性土)

(c) 地层损失率(砂卵石)

(d) 宽度参数(砂卵石)

图11相关性分布图

Fig. 11 Relevance distribution

黏性土地区隧道相对埋深的数值范围主要为1.5～3.8，沉降槽的地层损失率随着该量纲一的量参数的增大有近似减小的趋势,近似呈负乘幂的变化趋势；宽度参数随着该量纲一的量参数的增大没有明显的变化趋势。

砂卵石地区隧道相对埋深的数值范围主要为0.9～4.3，沉降槽的地层损失率随着该量纲一的量参数的增大有近似减小的趋势，近似呈负指数的变化趋势;宽度参数随着该参数的增大有逐渐减小然后增大的趋势,近似为二次多项式的变化趋势。

4.2 矿山法施工隧道

4.2.1 沉降槽最大沉降值

地表沉降槽的最大沉降值统计结果见图12。

剔除最终地表变形为单沉降槽的数值后，黏性土地层中矿山法开挖的59个地表沉降槽沉降最大值为43.00 mm，最小值为4.87 mm，平均值为24.55 mm，标准差为9.70 mm；近似为正态分布，主要分布在20～25 mm；偏态系数SK=-0.170，为左偏分布；峰态系数K=-0.513，为扁平分布。区间隧道局部为黏性土、砂土互层，存在潜水或承压水时，造成地表变形较大。

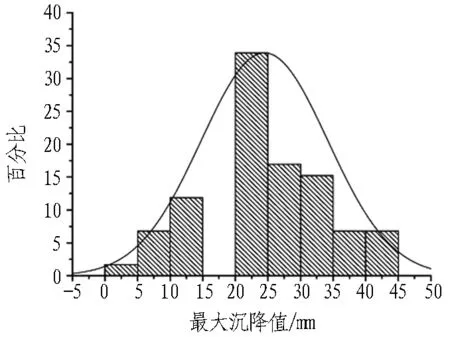
(a) 黏性土地层

(b) 砂卵石地层

砂卵石地层中58个地表沉降槽沉降最大值为32.69 mm，最小值为1.69 mm，平均值为15.49 mm，标准差为7.86 mm；近似为正态分布，主要分布在20～25 mm；偏态系数SK=0.079，峰态系数K=-0.788，为扁平分布。

4.2.2 地层损失率

地表沉降槽的地层损失率统计结果见图13。

(a) 黏性土地层

(b) 砂卵石地层

剔除拟合异常值后，黏性土地层47个地表沉降槽的地层损失率最大值为9.80%，最小值为0.90%，平均值为2.56%，标准差为2.17%，中位数为1.70%；近似为半正态分布，主要分布在1.0%～1.5%，约占总数量的34.05%。

砂卵石地层48个地表沉降槽中地层损失率最大值为9.96%，最小值为0.25%，平均值为2.66%，标准差为2.54%，中位数为1.53%；近似为正态分布，主要分布在1.0%～2.0%，约占总数量的29.17%。

黏性土与砂土的互层结构容易导致地表的较大变形，卵石地层可造成管棚施作困难、小导管注浆效果不良、注浆压力上不去等问题。地层存在空洞、上层滞水、地下管线渗漏等对地层变形控制也有很大影响。城市地层条件、环境条件对矿山法地表变形影响较大，同时，矿山法施工隧道也有一定的地层二次扰动效应问题。

4.2.3 宽度参数

地表沉降槽的宽度参数统计结果见图14。

(a) 黏性土地层

(b) 砂卵石地层

剔除拟合异常值后，黏性土地层中55个地表沉降槽的宽度参数最大值为1.16，最小值为0.23，平均值为0.49，标准差为0.21，中位数为0.43;近似为正态分布，主要分布在0.3～0.4;偏态系数SK=1.380，为高度右偏分布；峰态系数K=1.643，为尖峰分布。

砂卵石地层中69个地表沉降槽的宽度参数最大值为1.18，最小值为0.12，平均值为0.62，标准差为0.27，中位数为0.57；近似为多峰值分布，主要分布在0.4～0.5和0.8～0.9。

4.2.4 相关性分析

地层损失率和宽度参数与隧道相对埋深的相关性统计结果见图15。

黏性土地区隧道相对埋深的数值范围主要为1.2～4.3，该区段内地层损失率和宽度参数随着该参数的增大有逐渐减小然后增大的趋势，近似为二次多项式的变化趋势。

砂卵石地区隧道相对埋深的数值范围主要为1.2～3.3，该区段内地层损失率和宽度参数随着该参数的增大没有明显的变化趋势。

5 单线区间地表横向变形特性

北京地铁大断面单线区间的修建方法主要为盾构法和矿山法，单线隧道的沉降槽形态为单峰值型，沉降最大值一般出现在隧道的中心轴线上方附近。根据区间隧道开挖区域内的地层性质不同分别进行统计，统计结果见表2。

(a) 地层损失率(黏性土)

(b) 宽度参数(黏性土)

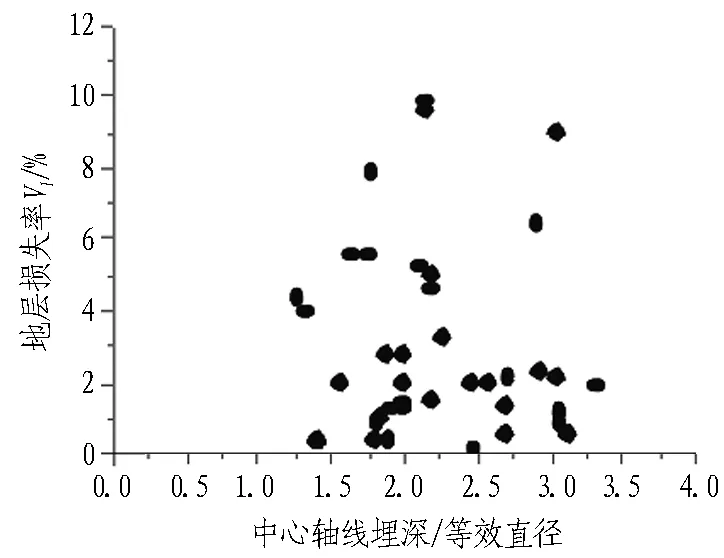
(c) 地层损失率(砂卵石)

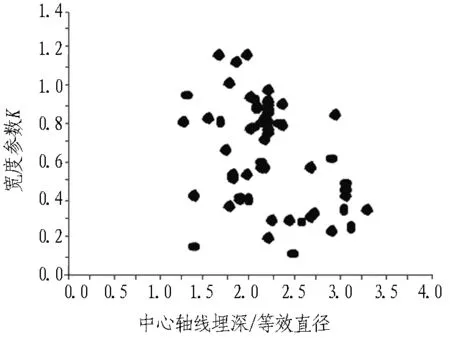
(d) 宽度参数(砂卵石)

图15 相关性分布图

由统计结果可知，北京地铁单线区间隧道的地表变形与施工方法和开挖地层密切相关，黏性土地层中采用盾构法施工的最大沉降值相对较小，平均值为21.51 mm，地层损失率和宽度参数的平均值也较小。

采用矿山法施工时，黏性土地层中隧道开挖可引起相对较大的地表沉降。受样本数量的影响，黏性土地层的地表沉降槽最大沉降值、地层损失率和宽度参数的平均值相对较小，但其标准差较大，整体数值分布较为离散。砂卵石地层较好的自稳性对减小矿山法施工对周围地层的扰动有一定的作用。

6 结论与讨论

1)根据隧道功能、地层性质、施工方法等分类研究了北京地铁隧道地表沉降槽的最大沉降值、地层损失率和宽度参数的分布形态，给出了相关统计结果及与隧道相对埋深的相关性。相关成果有助于北京地区或类似地层中地铁隧道工程的影响区、影响范围等的科学确定。

统计结果表明，矿山法车站在黏性土地层中的地层损失率平均值为1.85%，标准差为1.92%，宽度参数平均值为0.58，标准差为0.24；砂卵石地层中的地层损失率平均值为1.41%，标准差为0.88%，宽度参数平均值为0.67，标准差为0.14。

双线盾构法区间在黏性土地层中的地层损失率平均值为3.80%，标准差为2.54%，宽度参数平均值为0.53，标准差为0.21；砂卵石地层中的地层损失率平均值为3.78%，标准差为2.28%，宽度参数平均值为0.66，标准差为0.29。

双线矿山法区间在黏性土地层中的地层损失率平均值为2.56%，标准差为2.17%，宽度参数平均值为0.49，标准差为0.21；砂卵石地层中的地层损失率平均值2.66%，标准差为2.54%，宽度参数平均值为0.62，标准差为0.27。

2)城市地铁隧道施工引起的地表变形受城市环境条件、地层性质、施工方法、隧道埋深、隧道断面尺寸、双线水平间距等因素影响，应深入开展相关影响因素的研究。

3)随着我国城市地铁建设的不断开展，各地积累了大量的隧道工程地表变形资料，有必要对地表横向变形特性进行深入研究，以针对不同的城市地质条件提出适宜的地表横向沉降槽预测参数。