车轮多边形对不同结构类型轨道的动力影响分析★

郭 毅 胡 敏

(昆明铁道职业技术学院，云南 昆明 650217)

0 引言

我国高速铁路目前采用的板式无砟轨道主要有CRTSⅠ,CRTSⅡ和CRTSⅢ型3种，而对于特大型桥梁、黏土深路堑、松软土路堤或地震区域等不适于铺设无砟轨道的地段，通常采用有砟轨道[1]。车轮多边形现象广泛存在于轨道车辆车轮上，是表征车轮不圆顺的主要形式之一[2]。当动车组车轮出现多边形，高速运行时将形成强烈的高频轮轨冲击[3]。研究车轮多边形对不同类型轨道系统的动力影响，能够为动车组在线路上的适应性设计提供参考。

1 动力学模型

本文基于车辆—轨道耦合动力学理论[4]，建立了高速车辆—板式无砟轨道垂向耦合动力学模型和高速车辆—有砟轨道垂向耦合动力学模型，如图1所示。模型中，钢轨采用Timoshenko梁模型，3种板式无砟轨道在垂向上抽象为弹性基础上的叠合梁模型，仅结构和参数有所区别；有砟轨道的轨枕被视作刚体，考虑其垂向自由度，道床被离散成多个刚性质量块，考虑各块间的剪切刚度和阻尼。轮轨耦合关系均采用Hertz非线性接触理论计算[4]。

对于多边形车轮激励，国际上多采用含有1阶～N阶谐波的Fourier级数形式的位移函数来描述[4]，即:

其中，Ai为第i阶谐波的幅值；φi为相应的相位。

根据武广高铁动车组车轮多边形特征分析[3]，该线路上车轮多边形的阶次为17～20，本文选取15阶～22阶的单一车轮多边形进行计算，将其施加在1位轮对上，车辆与轨道参数见文献[5]～[7]。

2 动力学计算

2.1 速度对系统的动力影响

为分析不同速度等级下，相同车轮多边形对各类型轨道系统的动力影响，本节计算了车速为200 km/h～350 km/h时，CRTSⅠ,CRTSⅡ,CRTSⅢ型板式无砟轨道与有砟轨道的轮轨垂向力、轮重减载率、钢轨振动加速度以及扣件支反力的响应。其中，车轮多边形的阶次取为18阶，幅值取为0.05 mm，计算结果如图2所示。

从图2可以看出，当存在车轮多边形的动车组经过不同结构类型的轨道时，系统的动力响应均随着车速的增加而增加。当车速为350 km/h时，轮轨垂向力的最大值均超过《高速铁路工程动态验收技术规范》[8]规定的170 kN，但此时四种轨道的轮轨垂向力相差不大，反而是在车速为300 km/h时，差异性最为明显，CRTSⅢ型板式轨道时产生的轮轨垂向力明显较另外三种轨道大。对于轮重减载率，同样在300 km/h时CRTSⅢ型板式轨道明显较另外三种轨道大，均超过《高速铁路工程动态验收技术规范》[8]和《高速动车组整车试验规范》[9]规定的0.8，而当车速提高到350 km/h，此时轮重减载率均达到1，说明此时均发生了轮轨分离即“跳轨”。对于钢轨振动加速度，可以看出四种轨道的钢轨振动加速度相差不大，车速300 km/h时CRTSⅢ型板式轨道最大，CRTSⅡ最小，但是当车速达到350 km/h时，CRTSⅢ型板式轨道反而最小，此时CRTSⅠ型板式轨道最大。而对于扣件支反力，车速200 km/h时，四者差值较大，随着车速的提高，除CRTSⅢ型板式轨道外另外三种轨道相差不大，到350 km/h时，CRTSⅢ型板式轨道与其他三种轨道的差值缩小。

2.2 多边形阶次对系统的影响

通过上节分析可以看出，在车速300 km/h时，4种轨道所产生的轮轨垂向力等表现出较大差异，本节为分析车轮多边形的阶数对各系统的影响，计算车速设置为300 km/h，多边形阶次范围设置为15阶～22阶，幅值0.05 mm，计算结果如图3所示。

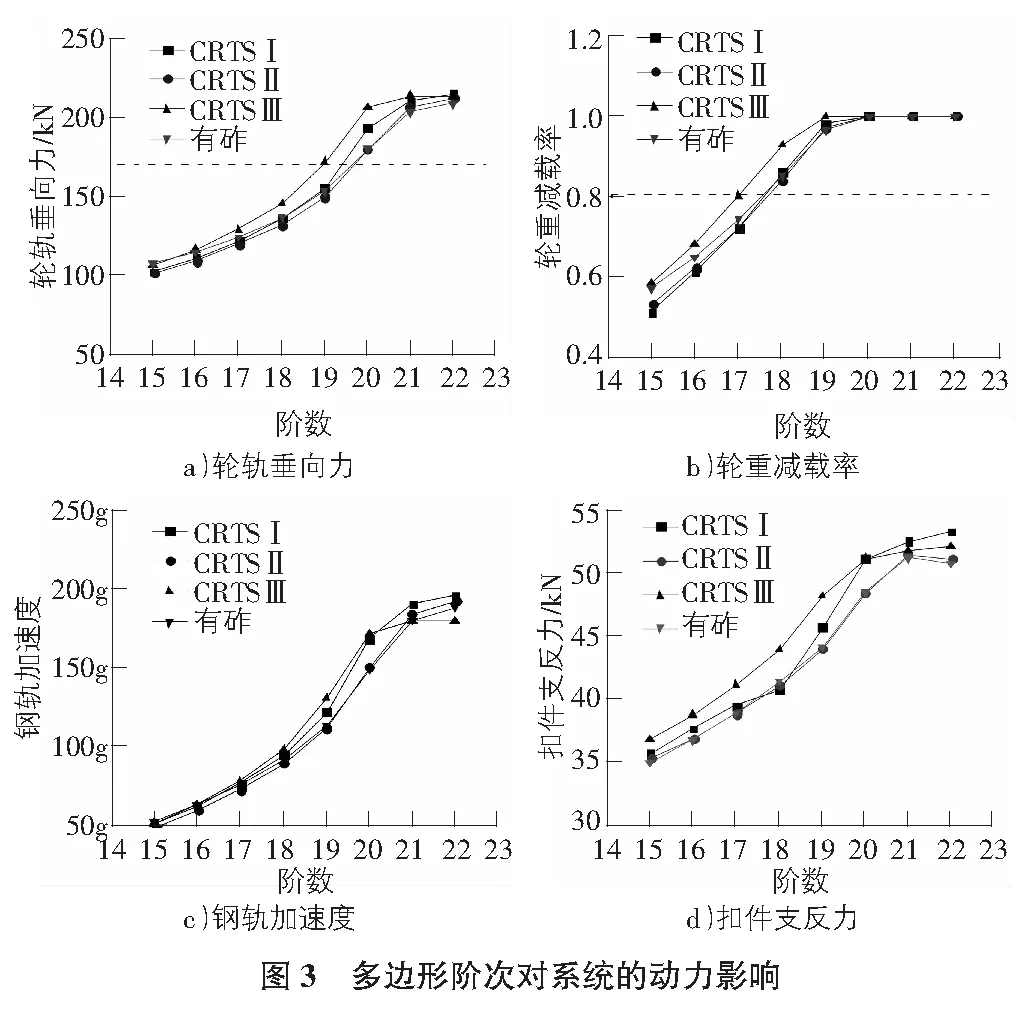
从图3可以看出，当存在高阶车轮多边形的动车组经过不同结构类型的轨道时，系统的动力响应均随着多边形阶次的增加而增加。对于轮轨垂向力，在15阶～20阶的范围内，随着阶次的增加，四者的差值逐步扩大，并且CRTSⅢ型板式轨道在19阶时达到171.97 kN，超过规范[8]规定的170 kN,而另外三种轨道产生的轮轨垂向力的最大值均小于170 kN。不过当车轮多边形的阶次增加到20阶时，4种轨 道所产生的轮轨垂向力均超过170 kN，此时CRTSⅡ型板式轨道和有砟轨道最小，而CRTSⅢ型板式轨道最大，而随着车轮多边形的阶次增加到21阶，4者轮轨垂向力的差值开始减小，到22阶时近乎相等，说明不同阶次车轮多边形对不同结构类型的轨道所产生的耦合振动是不一样的，在20阶时，最为明显。对于轮重减载率，CRTSⅢ型板式轨道在17阶时率先达到0.8，然后在19阶时达到1，即发生“跳轨”，而另外三种轨道直到阶次增加到20阶，轮重减载率才达到1。同时可以看出，在15阶～18阶范围内，CRTSⅠ型板式轨道轮重减载率最小，而在18阶～20阶范围内有砟轨道对应的轮重减载率相对较小，在整个范围内CRTSⅢ型板式轨道最大。对于钢轨振动加速度在15阶～20阶的范围内，随着阶次的增加，4种轨道的钢轨振动加速度的差值随着阶次的增加逐渐扩大，在这个范围内CRTSⅠ型和CRTSⅢ型板式轨道相对较大，另外两种轨道相对较小，而随着阶次的进一步增大，CRTSⅢ型板式轨道的钢轨振动加速度有减小的趋势，而另外三种仍然保持增大的趋势。对于扣件支反力，在15阶～20阶范围内，以CRTSⅢ型板式轨道最大，CRTSⅠ型板式轨道次之，CRTSⅡ型板式轨道和有砟轨道最小。而在20阶～22阶范围内，CRTSⅠ型板式轨道最大，CRTSⅢ型板式轨道次之，CRTSⅡ型板式轨道和有砟轨道最小。可以看出，不同阶次的车轮多边形对不同结构轨道系统的钢轨振动加速度与扣件支反力作用规律不相同，这与轨道系统的共振频率等有关。

2.3 多边形幅值对系统的影响

通过上一节的分析可以看出，当多边形阶次为20阶时，4种不同结构类型的轨道所产生的轮轨垂向力差值最大，为了进一步分析多边形幅值对不同结构类型轨道的动力影响，本节计算了车速300 km/h情况下，20阶车轮多边形对各系统的动力影响，幅值范围为0.01 mm～0.06 mm，计算结果如图4所示。

从图4可以看出，当存在高阶车轮多边形的动车组经过不同结构类型的轨道时，系统的动力响应均随着多边形幅值的增加而增加。对于轮轨垂向力来说，随着幅值的增加四种结构类型的轨道在0.05 mm时的差值最大，这与各轨道结构对冲击载荷的响应不同有关，因为此时4种轨道均发生了“跳轨”，在整个计算范围内可以看出，以CRTSⅢ型板式轨道最大，CRTSⅠ型板式轨道次之，CRTSⅡ型板式轨道和有砟轨道最小。对于轮重减载率，CRTSⅢ型板式轨道在0.04 mm时即发生“跳轨”，其值为1，另外三种轨道在0.05 mm时才发生“跳轨”，即其值为1，可以看出在整个变化范围内四种轨道对应的轮重减载率大小与轮轨垂向力一致，直到其值达到最大值1。对于钢轨振动加速度和扣件支反力的大小来说，在整个计算范围内仍然以CRTSⅢ型板式轨道最大，CRTSⅠ型板式轨道次之，CRTSⅡ型板式轨道和有砟轨道最小。

3 结语

不同结构类型轨道系统对车轮多边形的动力响应，随着车速、多边形阶次和幅值的增加而增加。四种轨道系统在车速为300 km/h，车轮多边形阶次为20阶时，动力响应所表现出来的差异较为明显，以CRTSⅢ板式轨道最为剧烈，CRTSⅠ板式轨道次之，CRTSⅡ型板式轨道和有砟轨道最小。本文以一种车型为例分析了车轮多边形对不同结构类型轨道的动力影响，但是由于各型动车组车辆结构和参数的不同，车轨耦合系统的动力响应会有所不同，要全面掌握车轮多边形对系统的动力影响，应全面开展各种类型的动车组与各种类型轨道系统的动力响应分析。