基于应力迁移法的边坡稳定性分析

李 小 敏

(浙江工业职业技术学院建筑工程学院，浙江 绍兴 312000)

1 概述

目前边坡稳定问题的分析方法比较多，流行的方法主要有极限平衡法、非连续变形分析法、有限元法、可靠度法与模糊数学法等[1-4]。这些方法在不同的工程和项目中都有应用，在长期的工程分析中积累了大量的经验，目前边坡稳定分析方法已比较成熟。2004年，徐金凯和李小勇[5]在对边坡多方面研究和分析的基础上提出了应力迁移法。该方法与本文提出的应力迁移法，在基本思想的提出和方法的推导过程上都有着本质上的区别，仅在名称上相同而已。本文在总结一般强度折减法的研究基础上，提出了基于折减的应力迁移法，对其进行了探索并验证其可行性，本文主要作了以下几方面的研究及工作：

1)本文概述了强度折减有限元法的提出和基本思想，在假定单元竖向应力保持不变以及折减前后大小主应力方向不变的条件下，给出了应力迁移法的计算公式。

2)介绍了应力迁移法在ABAQUS软件中的操作步骤。

3)通过典型算例验证了应力迁移法的正确性和适用性。

2 应力迁移法的基本思想

2.1 一般强度折减法

Zienkiewicz[6]于1975年首次提出了强度折减，很多专家和学者对这一新的概念进行了探索和研究，但基本研究思路都和提出者的思想差别不大，具体的公式如下:

(1)

令：

(2)

则：

τr=σtanφr+cr

(3)

式中：c，φ——土体实践强度指标；

φr，cr——折减的强度指标。

2.2 应力迁移法的提出

应力迁移法具有理论上的可行性并且比较符合实际情况，在有限元计算中，必须先计算坝体特别是上游坝壳料因湿化变形因素引起的等效节点力。计算引起湿化变形的等效节点力基本思路是,先假定土体湿化变形被约束，然后解除约束将等效节点力列阵施加于土体上[7,8]。

现在我们将运用于土石坝的湿化变形的处理方法运用于边坡的处理，将折减后的应力迁移到节点力上，并将节点力作用于各个节点，直至边坡破坏，这就是应力迁移法。下面进行该方法的公式推导。

2.3 应力迁移法的公式推导

2.3.1基本假定

1)假定折减前后σr不变；

2)假定折减前后大小主应力方向不变。

2.3.2由初始状态求解极限状态

由图1可以看出，应力圆①是仅考虑自重情况下的应力初始状态，这种状态下单元体尚未达到破坏状态，应力圆②则是在上述假设条件下得到的极限应力状态，相对应力分别为σ1f,σ3f。即已知σx0，σy0，τxy0求解σ1f，σ3f。经过推导可得:

(4)

(5)

2.3.3由极限状态求解折减后的状态

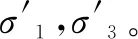
(6)

(7)

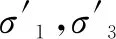
3 ABAQUS在应力迁移法中的应用

边坡模型建好后，如何采用有限元软件对应力迁移法进行分析至关重要，分析中对单元体进行应力和节点力的提取也是分析的关键，具体操作如下：

1)提取有限元模型在初始应力即自重应力下的初始应力分别为σx0,σy0,τxy0；

2)运用有限元软件或相关程序将分析的结果数据导出分别为σx0,σy0,τxy0，然后通过折减系数Fr，采用前面应力迁移法推导公式进行数据处理得出Δσx,Δσy,Δτxy；

3)对有限元模型的自重应力和模型边界条件进行去除，并对有限元模型单元体的节点位移进行约束，然后将前面折减后的数据Δσx,Δσy,Δτxy对单元进行加载，经过有限元分析可得出各个节点的节点力RF；

4)对初始的有限元模型相应的单元节点反向施加节点力RF，经过有限元分析后则应力迁移法的有限元分析完成，通过上述分析可以得出在某一特定折减系数下边坡的受力情况，然后根据相应的判断标准评价边坡的稳定性情况；

5)通过边坡稳定性的判断，确定边坡是否失稳，如果失稳则分析结束，如果没有达到失稳，则应当进一步增大折减系数，并按上述步骤再次进行分析，直至边坡失稳，这种状态下的折减系数就是所求的边坡安全系数。

4 算例分析

设有一均质边坡坡高20 m，坡比1∶1，其几何轮廓如图3所示。土料参数列于表1。

4.1 应力迁移法分析

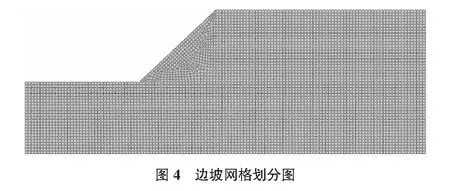
边坡的边界条件为左右边界水平支座，下部铰连接。采用四节点四边形平面应变单元，网格划分如图4所示，模型由5 404个单元组成，节点总数为5 580。计算中采用理想M-C弹塑性本构模型，不考虑剪胀，即令剪胀角ψ=0。

表1 边坡土料参数表

通过研究基于应力迁移法计算分析，各种判据的安全系数如下所示:

1)有限元计算不收敛判据。

经过应力迁移法的计算，当折减系数Fr增大到1.25时计算不收敛(此时算出的位移不是Fr=1.25时对应的位移，得到的位移值偏小)，故若以有限元计算不收敛作为失稳判据，则安全系数为FS=1.25。

2)特征点位移突变判据。

计算研究中将坡顶点A、坡中点B以及坡脚点C作为特征点，如图3所示(图中并未给出所有折减系数对应的位移点，下文相同)。各特征点与各方向位移给出的安全系数统计在表2中。由表2可知，如果以位移突变作为失稳判据，则安全系数为FS=1.23。

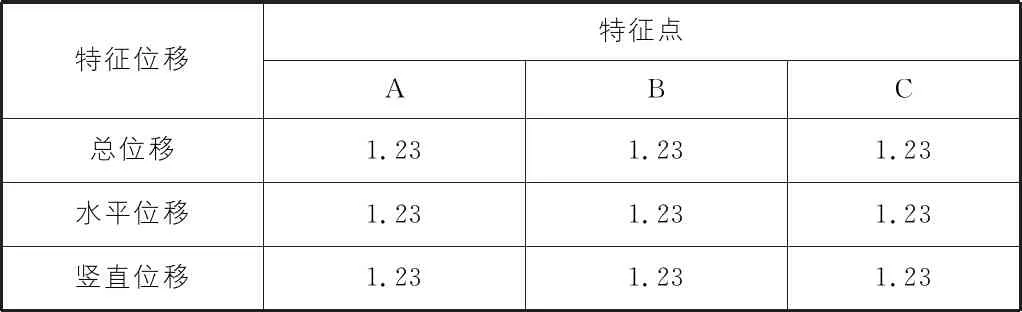
表2 特征点位移安全系数统计表

3)广义剪应变贯通判据。

若以广义剪应变贯通为失稳判据，则安全系数FS=1.23。

将上述三种判据得到的结果列于表3中。

表3 判据安全系数表

由表3可以看出，三种失稳判据得到的安全系数相近，其中位移突变判据与广义剪应变贯通判据给出了相同的结果，一旦边坡内形成了贯通的广义剪应变区，意味着某些点的位移将产生无限制的流动。随着广义剪应变区的扩大，发生位移流动的点越来越多，程序将因不能满足预设的收敛准则而终止计算。

综上，用应力迁移法进行算例边坡稳定性分析，取最小安全系数，得出的安全系数可以取为FS=1.23。为了校核应力迁移法的准确性，下面将运用极限平衡法计算算例，与应力迁移法进行对比分析。

4.2 极限平衡法分析

极限平衡法计算程序采用GEO—SLOPE公司开发的GeoStudio2004的SLOPE/W模块。计算结果如图5与表4所示。

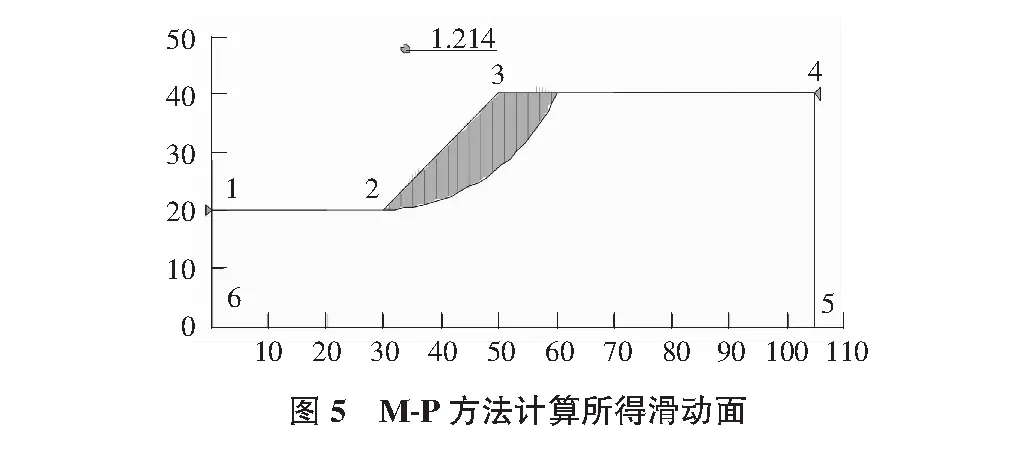
表4 各条分法安全系数统计表

4.3 各种方法对比分析

在本算例中以位移突变和广义剪应变贯通为判据得到的安全系数与极限平衡法较接近，但是用应力迁移法得到的安全系数比用极限平衡法得到的大，不过其误差较小。

综上所述，通过应力迁移法计算得出的安全系数虽然比极限平衡法得到的安全系数要大一点，但是都只有较小的误差，故应用应力迁移法对算例进行稳定分析是可行的。

5 结语

本文在推导出的应力迁移法公式的基础上，基于ABAQUS软件进行数值模拟，对边坡典型算例运用应力迁移法进行了稳定分析计算，并将计算结果分别与极限平衡法和一般强度折减法进行了对比分析，得出如下总结：

1)虽然运用应力迁移法计算出的安全系数要比极限平衡法大一些，但是其误差都是比较小，是在可以接受的范围内，故应力迁移法在边坡稳定分析中具有适用性与合理性。

2)在应力迁移法中，广义剪应变贯通在失稳判断方面和位移突变的效果基本一致，计算不收敛则比前两者作为失稳判据在安全系数上更大。

3)强度折减法对边坡所有处土体强度参数进行折减，得到贯通的等效塑性区域，通常认为是滑动带。边坡实际上常沿软弱结构面发生滑动破坏，强度折减后的应力场与位移场是虚拟的，只能得出一个大概的破坏机理，并不能准确标志滑动面，应力迁移法也是如此。