基于ANSYS有限元软件的桥梁结构拓扑优化★

白鸿宇 赵超凡 罗沪生 胡 豹 邓兴辉

(南京工程学院建筑工程学院,江苏 南京 211167)

0 引言

随着交通的逐渐进步，设计要求也是日渐提升。而对结构进行拓扑优化可以达到强度、刚度、耐久性以及稳定性的要求，使繁冗的设计更加简单，并有更高的质量。结构的拓扑优化能够使材料最简化、强度利用率最大化、经济性合理化。在结构优化中拓扑优化是较难实施的一种优化方式之一，伴随着这种挑战的是其能带来巨大的经济效益以及更加合理的土木工程结构形式。其研究思想是将结构拓扑优化问题转变为某一特定区域内寻求最佳的材料配置问题，使得结构满足一切有关平衡、应力以及位移等约束条件的情形下具有最优的性能指标[1]，通过求得结构最优的优化情况使结构桥梁工程是交通工程中重要的组成部分。而复合材料的高昂价格又使其无法大规模生产使用，使得复合材料在实际施工过程中难以成为建设过程中所使用的主要材料，因此通过使用拓扑优化分析技术对复合材料结构进行精简就显得尤为重要。

本文讲述了以碳纤维预浸料作为基础材料，以桥梁结构强度作为分析对象，通过实际案例利用ANSYS有限元软件对碳纤维复合材料的桥梁结构进行拓扑优化得出最终的优化结果。

1 结构优化的基础模型

结构的拓扑优化是一门新兴的概念化的学科，是只需设定优化结构的空间范围以及荷载与支撑边界等条件，然后再通过使用受力分析和迭代计算的方式就能自行找出最合理的结构优化模型，是一种以计算机为计算基础的结构模型优化技术。

目前拓扑优化研究较为成熟，其中基于各向同性材料的变密度法[2]已被运用到很多商用优化软件中。变密度法本质上是{0，1}[3]离散变量组合优化的问题，通过优化计算保留有利的单元，删除作用不大的单元，因而可得以下数学模型：

其中，Xi为变量，取0或1(0表示删除单元格，1表示保留单元格)；n为设计变量个数；K为总刚度阵；U为结构的位移向；F为结构所受外力向量；V为结构的体积；V*为优化后结构体积的上限值[4]。

但是由于拓扑优化设计变量很多，按{0，1}变量组合优化，易出现组合爆炸问题，因此设计中常常将设计变量松弛为连续变量，采用如下变密度法的形式：

Findρ={ρ1，ρ2，…，ρn}。

MinC={U}T[k]{U}。

s.t.[K]{u}={F}。

0≤ρmin≤pi≤1,i=1,2,…,N。

其中，ρi为离散单元的相对密度，取值在[ρmin，1]之间的连续值；N为设计变量个数；K为总刚度阵；U为结构的位移向；F为结构所受外力向量；v为结构的体积；v0为优化后结构体积的上限值;取ρmin=0.001。

拓扑优化还有基于“微结构”思想的均匀化方法、进化结构优化方法、水平集法、两相法、泡泡法[5]等等。

目前，连续体拓扑优化的研究已经较为成熟，其中基于各向同性材料的变密度法已经被应用到商用优化软件中，在这中间有一些比较著名的公司所出品的软件如美国Altair公司开发的软件Optistruct以及德国Fe-design公司开发的Tosca等[6]。

2 ANSYS有限元分析流程

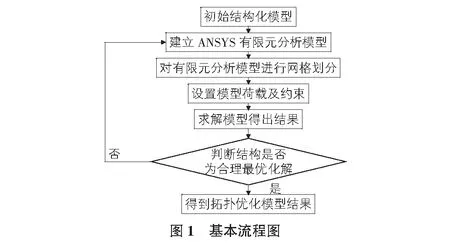
本次研究项目过程中对于ANSYS有限元分析的操作流程如下：1)根据实际案例确定所设计模型的尺寸、大小及优化方式等；2)针对受力条件和模型的用途确定设计区域，约束条件；3)根据分析类型确认结构模型网格划分的方法；4)按照给出确认的设计区域及约束条件进行设置；5)提取有限元分析结果；6)采用拓扑优化对得到的数据进行分析;7)在拓扑优化后结果基础上再设计；8)重复上述七步得到合理适用的最优化结构模型。

图1为本研究过程中有限元分析的基本流程图。

3 拓扑优化的实际案例

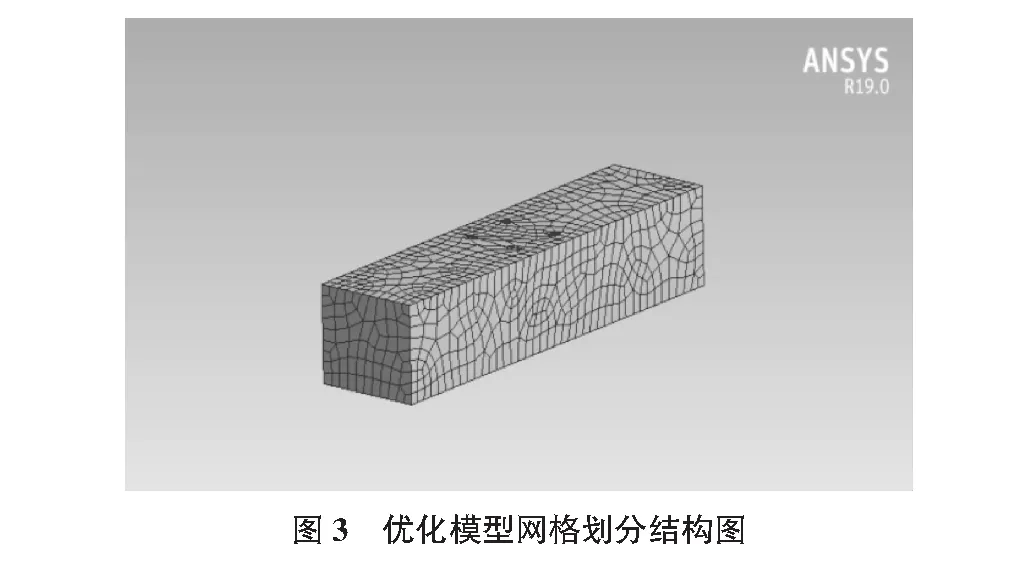
本研究实例要求桥梁的最小尺寸为长600 mm，宽100 mm。规定桥梁路面(通行面)必须是平整的且不能通透，满足“四轮小车”从桥的一头运动到另一头时桥路面不能有损[7]。为了满足弯曲加载支座的有效尺寸要求，桥梁的宽度不能超过 150 mm。桥梁的中间必须无障碍，以便加载杆和“小车”可以定位施载。桥底面不允许有任何支撑结构。桥梁竖向形变需小于25 mm，桥载荷能力P需大于14 kN。图2为平面设计条件示意图，展示了本研究实例具体的受力情况，图3为空间优化模型及网格划分结构图，是原图2模型的空间立体展示图，网格划分的目的是为了后期拓扑优化的过程中方便对单元格进行删减。

3.1 优化过程

基于给出的ANSYS有限元分析流程对上述模型结构进行有限元分析可以得出如图4所示的应力应变分布图。

通过图4可以看出应变集中处拥有较大变形，而约束附近存在不受力单元，为可优化单元，受力最严重变化最大的往往集中于结构中部，结构两侧部分区域呈现浅灰色意指受力微弱或不存在受力。通过采用拓扑优化模块对上述模型进行优化，上述结构中低受力单元格和零受力单元格被删减或削弱，在保证满足原有功能的基础上，拓扑优化得到了如图5所示的初步优化结构图。

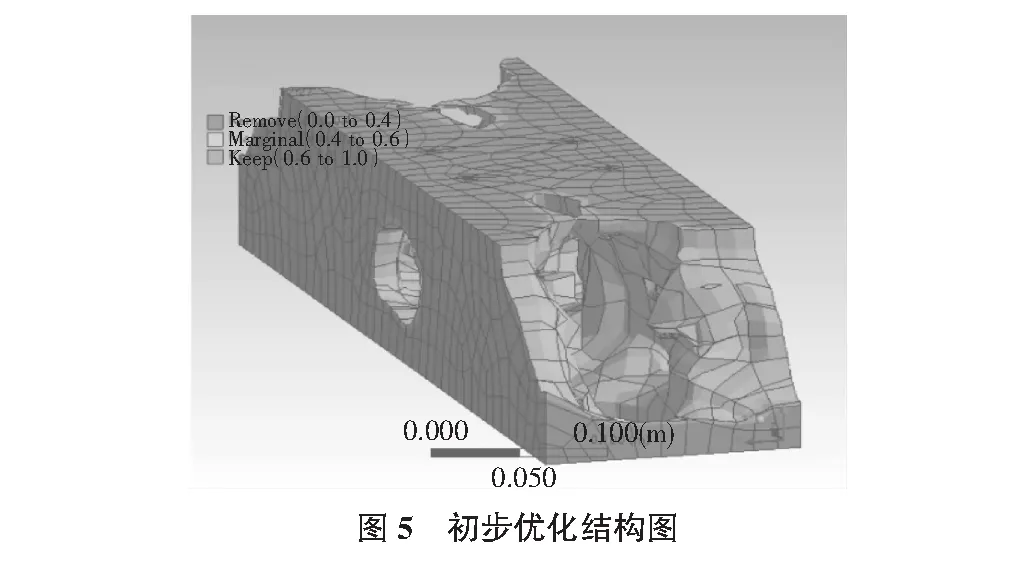
从图5中可以清晰的看出模型优化后减少了近一半的体积，中间部分受力薄弱处被挖空，两边存在的零受力单元格也都得到了削减，结构整体被优化了，但由于优化后结构不规则并不能实际应用于模型搭建和施工中，需要在此基础上二次设计再次优化，二次设计再优化的意思是指利用图5所展示的结构作为设计结构本体，在其框架上进行设计，制造出拥有平滑桥面，满足小车通行条件，同时能让桥梁结构支撑部分得到进一步优化的桥梁结构而进行的人为优化设计，再对所做的人为优化设计进行力学测试后满足形变要求、稳定性和力学性能要求即可作为桥梁设计的方案之一。以下为再优化设计的步骤。

首先将图5模型原件套入ANSYS建模框架中通过使用ANSYS自带的图模构筑软件对上述结构填补消减优化，在保证大体结构的同时使桥梁上表面更加的平滑，经过设计后得到了如图6中所示上部呈现微弧形，中部挖空的几何体。

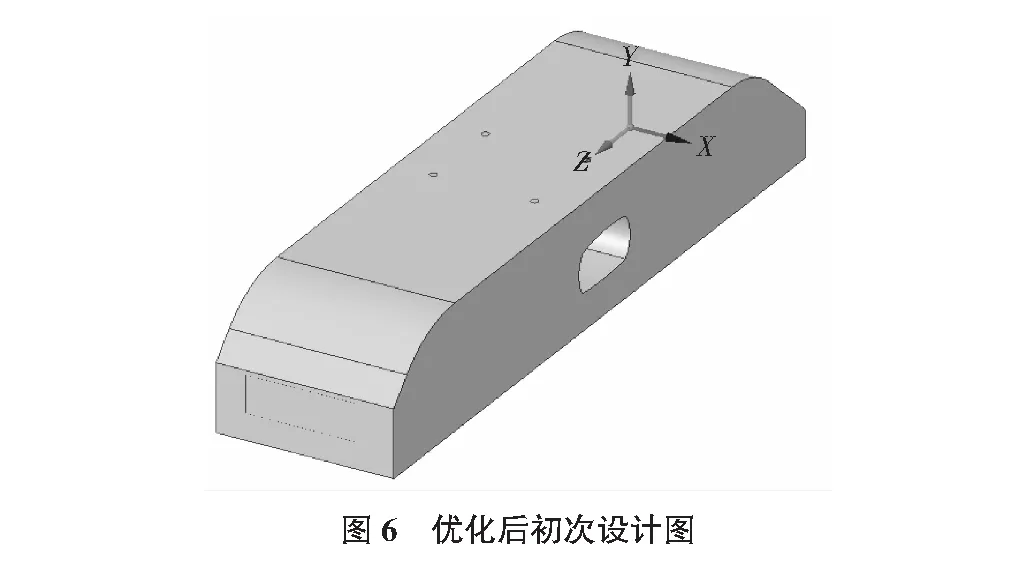
上述图6结构依然未达到结构最优解需要再次对其进行优化和设计，通过重新将该模型导入软件中对该结构进行分析设计和优化，接下来重复上述过程，以得到预期的优化结果。

图7，图8显示了在优化递进的过程，该模型结构的实际演化过程，可以看出优化结构呈现出中间挖空，两端内凹的现象，针对这一特性进行了多次优化设计最终得到了如图9所述的优化结果。

表1 优化前后体积质量变化表

综上所述拓扑优化过程中减少了原桥梁结构60%左右的体积，表1显示了桥梁优化前后尺寸的具体变化。

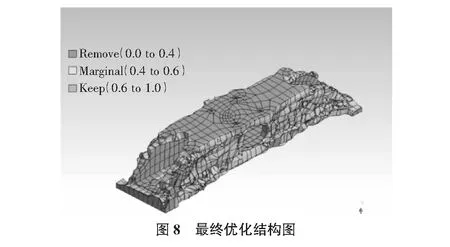
3.2 优化结果

在对优化过的结果进行多次优化设计以后可以得到上述图9所示的碳纤维复合材料桥梁，通过分析其应力应变性能可以得到如图10，图11所示的分析图。

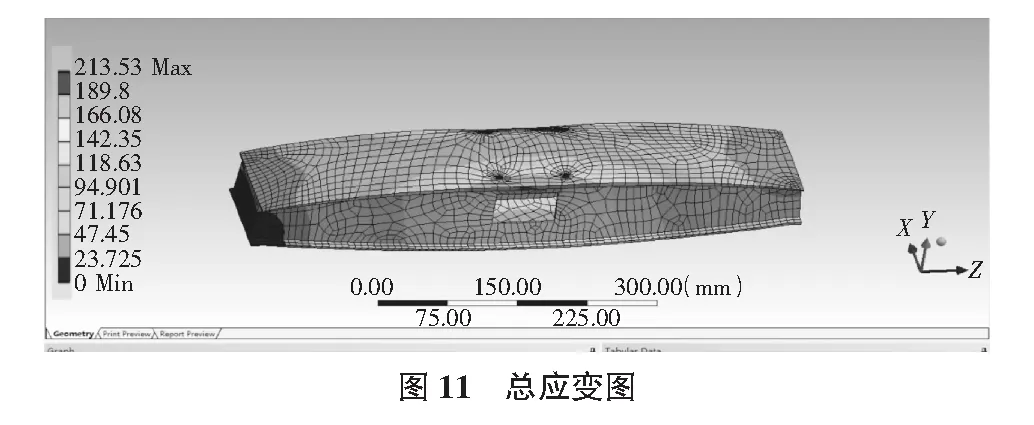
通过观察图示可以看出最终设计结构形变量远小于极限值，同时强度也满足要求，受限于材料性能4个施力点处有可能发生脆性破坏，后期通过人为设计局部加强，可以提高桥梁稳定性，同时避免此类脆性破坏发生。

4 结论与展望

本文以桥梁结构强度为最大优化目标，确定约束荷载后，通过使用商用有限元分析软件ANSYS对结构进行了分析以及拓扑优化设计，通过拓扑优化设计可以获得初步阶段的轮廓布局，之后再重复优化步骤，可以得到较为理想的结果。本文最终优化结果体积与重量为初始体积与重量的30%左右，大大削减了复合材料的用料，同时说明了复合材料作为结构构件参与桥梁建设成为了可行的方案。希望未来有限元分析软件能更加快捷便利的在各项工程方案中得到使用，在结构设计过程中，帮助工程师解决强度刚度稳定性计算和设计方面的困扰，为桥梁结构建设添砖加瓦。

注:图表来源：本文所有图表均取自ANSYS研究实验分析截图。