定性结构力学中的静定平面桁架★

高 倩 韩明岚 高丽燕

(青岛理工大学理学院，山东 青岛 266033)

目前，结构力学的教学依然是以传统的经典结构力学为主，偏重于手算,偏重于定量计算的原理和方法，计算能力小，速度慢，不能满足实际工程的需求。随着计算机的普及，求解器、有限元等结构模拟计算(在文中统称为结构力学仿真)逐渐满足了这一需求，但对庞大计算结果的正确与否还缺少判断，越来越多的专家学者和高校教师认为定性结构力学(又称为概念结构力学)可以填补这一空白[1-3]，但定性结构力学还处于探索形成阶段，本文对定性结构力学中的静定平面桁架部分做了有益的探索。教学中，定性结构力学、经典结构力学以及结构力学仿真(文中应用的是求解器)在求解静定平面桁架时，其偏重点是不一样的。

1 静定桁架在经典结构力学中的偏重点

经典结构力学偏重于手算，偏重于定量计算时的原理和方法，具体到桁架结构的教学中，主要在于结点法、截面法和平衡方程的应用，通常会让学生求解某些指定杆的内力，文献[4]就是让求解图1a)中JL，JD，CD三杆的轴力。

2 静定桁架在定性结构力学中的偏重点

定性结构力学主要用于估算，用于对定量计算结果的判断。对于静定平面桁架，应用的方法不仅仅是结点法、截面法以及平衡方程，一切可能的方法均可以利用，在内力求解上，主要是估算杆的拉压性能，比较某两根杆轴力的相对大小，确定某杆内力的范围等。下面还是以图1a)为例，详细说明如何进行静定平面桁架的定性分析。

1)确定上弦杆和下弦杆的拉压性能。图1a)中所有上弦杆均为压杆，所有下弦杆均为拉杆，因为这是一个梁式桁架，该桁架的受力可由与之对应的简支梁(如图2所示)的变形和内力来比拟，通过图2简支梁的M图可知，简支梁的变形是上压下拉，所以该桁架的上弦杆受压，下弦杆受拉。

2)估算腹杆轴力的大小，以及各上弦杆之间、各下弦杆之间轴力的相对大小。对于该桁架，其腹杆的轴力较小，主要受力杆件为弦杆，且弦杆之间的内力分布比较均匀。

这是因为当桁架的形状与合理拱轴线趋近时，桁架就类似于一个具有合理轴线的空心拱，这样的拱其弯矩和剪力都很小，而桁架中腹杆的轴力可由拱的剪力来比拟，所以腹杆的轴力随之较小，则主要受力杆为弦杆，且各上弦杆之间以及各下弦杆之间的轴力比较接近，而合理拱轴线的形状又与相应简支梁的M图成正比。比较图1a)和图2可知，桁架左半跨的形状与M图比较接近，右半跨二者差别较大，但右半跨荷载较小，所以该桁架腹杆的轴力较小，且弦杆之间内力分布比较均匀。

3)比较某两根杆轴力的相对大小，甚至利用一些特殊结点能迅速求出某些杆的实际值。

a.由桁架的特殊结点可知，结点B为“T”型结点，见图1b)，所以FNBA=FNBC，且FNBH=0；同理，结点F也为“T”型结点，FNFE=FNFG，FNFT=0。

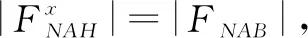
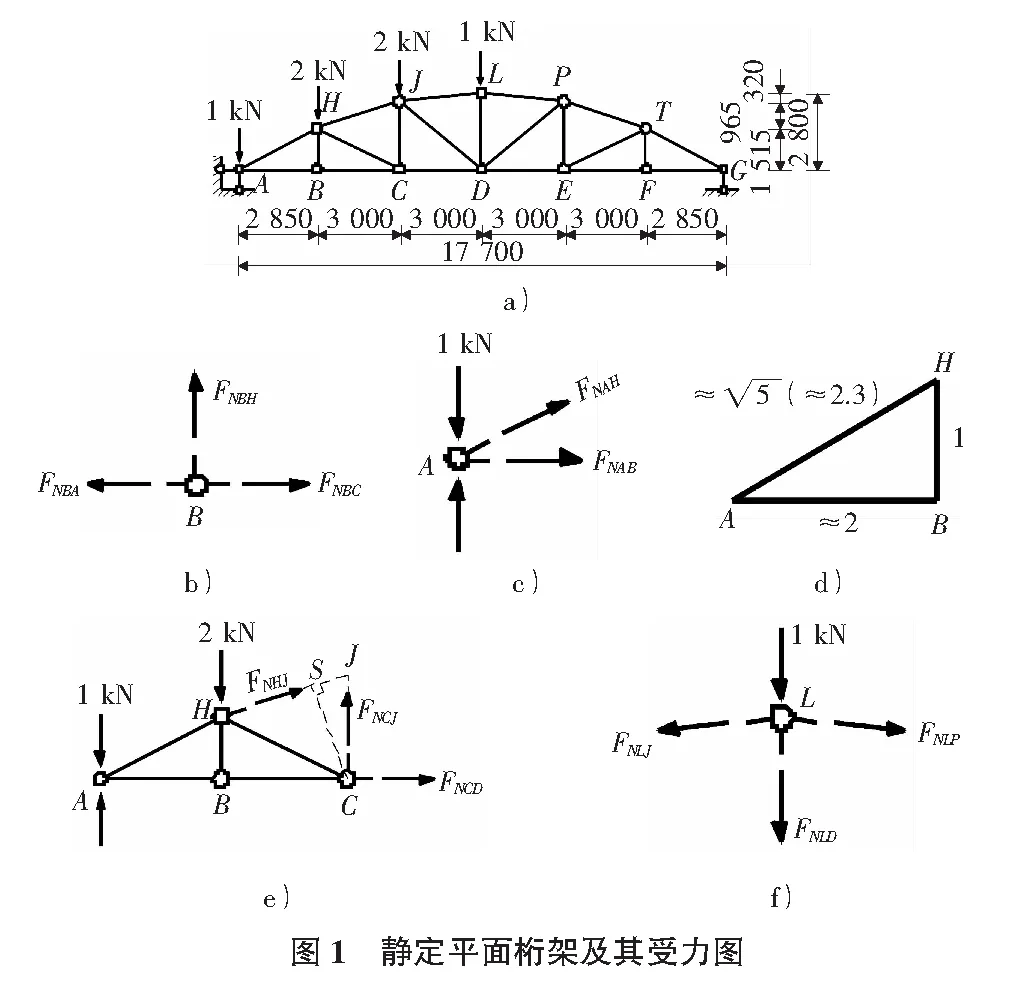
c.从图1e)的受力图可知，∑MC=0⟹FNHJ，∑MJ=0⟹FNCD，因C与J位于同一条竖直线上，所以受力图上的所有荷载和反力对这两个矩心的力矩是相同的，但FNHJ到矩心C的力臂SC比FNCD到矩心J的力臂JC略小，所以|FNHJ|>|FNCD|，同理|FNTP|>|FNED|，但都只是略大。

4)左半跨与右半跨相比，左半跨的轴力值(文中指轴力的绝对值)应高于右半跨，因为左半跨与右半跨的结构形状和尺寸均相同，但主要荷载位于左半跨，所以左半跨的内力应高一些，且该桁架的主要受力杆件为弦杆，所以这个结论主要针对上下弦杆而言。

5)利用一些简单受力图，可以快速估算出某些杆的内力范围，以此来判断仿真计算结果的可靠性。

b.图1c),图1d)分别为A点的受力图和ΔABH尺寸的大概比例，又已知FAy≈4.5 kN，从而可快速估算出|FNAB|≈(4.5-1)×2=7 kN，|FNAH|≈3.5×2.3≈8 kN，同理，可估算出|FNGF|≈1.5×2=3 kN，|FNGT|=1.5×2.3≈3.5 kN。

定性结构力学中的估算，并不是说一点儿定量计算也不做，而是指不要过于依赖“定量计算”，定量计算与定性计算的关系就类似于“树木”与“森林”的关系，教学中若是只依靠经典结构力学和结构力学仿真，容易形成“只见树木不见森林”的后果，所以在结构力学教学中，训练学生的定性求解思维是非常必要的。

3 静定桁架在结构力学仿真中的偏重点

结构力学仿真(这儿应用的是求解器)的偏重点与经典结构力学和定性结构力学均不同，其最大优势是能快速求出整个结构所有杆的内力，教学中，对于静定桁架而言，结构力学仿真可以偏重于各类相似桁架之间的对比，从而找出杆的内力与形状和尺寸之间的规律，本文对三角形桁架、抛物线形桁架、平行弦桁架、梯形桁架做了比较。

1)三角形桁架的求解器结果如图3a)所示，右半跨的结果特别有规律，腹杆内力全为零，上弦杆轴力均为-4.92 kN，下弦杆轴力均为4.70 kN，这是因为右半跨与图2中M图的形状相同，即桁架的形状与合理拱轴线重合，所以右半跨腹杆的内力均为零，且弦杆之间内力分布均匀，但左半跨的形状与合理拱轴线相差较大，从而没有这个现象。

2)图3b)所示为抛物线形桁架的内力，其腹杆内力均很小，左半跨各弦杆之间、右半跨各弦杆之间内力分布都比较均匀，因为桁架结构左半跨的形状与图2中M图相似，右半跨虽然相似度没有左半跨更好，但右半跨的荷载非常小，所以出现了这种结果，前面也已分析过。

3)平行弦桁架的求解器结果如图3c)所示，各腹杆之间、各上弦杆之间以及各下弦杆之间内力分布都很不均匀，因为平行弦桁架的形状与合理拱轴线相差最大，所以各部分的内力分布最不均匀。但该桁架弦杆轴力的最大值(绝对值)为5.21 kN，另三类桁架分别为11.68 kN,7.49 kN,6.35 kN，对比来看，该桁架的最小，原因是作为上弦的压杆与作为下弦的拉杆共同构成了一个力偶，其数值大致与图2中的M图相一致，而上下弦之间的距离关系到力臂的大小，在端部，平行弦桁架的力臂最大，所以其弦杆的轴力最小，而三角形桁架在端部的力臂最小，所以弦杆轴力最大，另两类桁架介于二者之间。

4)图3d)为梯形桁架的内力结果，介于平行弦桁架和抛物线形桁架之间，从外形上看，该梯形桁架与平行弦桁架更相似，所以各杆轴力值也与平行弦桁架更接近。

4 结语

经典结构力学、定性结构力学、结构力学仿真三者的偏重点是不一样的，但并不是孤立存在的，而是相互补充、相互解释的。经典结构力学属于手算方法，结构力学仿真则属于电算方法，手算的计算能力小，速度慢，但方法和原理清晰明了，而电算的运算能力大，计算速度也快，但结果正确与否不得而知，二者是两种极端的定量计算方法，定性计算恰好可以填补二者的空白。 定性结构力学应该在学习了经典结构力学的基本方法和原理之后再开设，在实际工作中，定性计算可用于对电算结果正确与否的判断，所以发展定性结构力学势在必行。