地铁车车头脚蹬可靠性分析及优化设计
2020-06-05傅振亮田雪艳李永华
傅振亮,李 娜,田雪艳,温 昕,李永华⋆
(1.中国中车唐山机车车辆有限公司产品研发中心,河北唐山063500;2.大连交通大学机车车辆工程学院,辽宁大连116028)
0 引言
地铁车车头脚蹬作为城轨列车重要的支撑承载部件,需承受较高的正交载荷,其可靠性是保证车头安全运行的重要指标。若采用不确定性方法对脚蹬的强度进行可靠性分析,其最大应力有一定的概率超出材料的许用应力,因此,为保证脚蹬踏板的承载能力和安全使用,对其进行强度可靠性分析是十分必要的。
目前,针对强度可靠性分析的研究很多,曹炜等[1]采用Monte Carlo方法对拉壳钩强度可靠性进行评估与分析。周新建等[2]对某1.5MW双馈式风力发电机风机主轴进行基于静强度的结构可靠性分析。蔡德咏等[3]采用可靠性与有限元相结合的方法对火箭炮发射箱箱体进行了刚强度分析及优化设计。胡登高和范迅[4]应用有限元法对液压支架进行强度、可靠性和敏感性分析。智鹏鹏[5]等对转向架构架进行结构强度可靠性分析。本文以某地铁车车头脚蹬为研究对象,选取脚蹬的最大Von.Mises应力作为结构性能响应建立极限状态方程,采用基于拉丁超立方采样的Monte-Carlo法对其进行强度可靠性分析,得到了脚蹬的最大Von.Mises应力和极限状态函数值的概率分布特征,获得了脚蹬的强度可靠度。在此基础上,采用OptiStruct结构优化技术对脚蹬进行尺寸优化,为提高脚蹬的可靠性提供了参考。
1 强度可靠性分析原理及方法
1.1 应力-强度分布干涉理论
应力-强度分布干涉模型如图1所示,s为结构应力,S为结构强度,阴影部分为s和S的干涉区,可能出现Ss的情况,此时结构将发生失效,因此即使保证安全系数大于1,s与S的概率密度还会出现干涉区,所以只用安全系数来反映结构是否安全是不够充分的,必须进行可靠性分析。已知s和S的概率密度函数可得可靠度的计算方程为

式中:f(s)为应力的概率密度函数,f(S)为强度的概率密度函数。

图1 应力-强度干涉模型
1.2 强度可靠性分析极限状态方程
根据应力-强度分布干涉理论,设x1,x2,…,xn为设计变量,则极限状态方程为

式中:[σ]为材料的许用应力;σmax为结构的最大节点等效应力。
2 脚蹬可靠性分析
2.1 脚蹬可靠性分析过程
Monte-Carlo法是对输入变量进行大量抽样,失效点落在安全区外的个数占采样总数的比率即为结构的失效概率[6]。而基于拉丁超立方采样的Monte-Carlo法将输入变量的取值范围分成n个区间,每个变量在每个区间内只能“撞击”一次,因此,不会出现采样点重叠的现象[7]。
基于Monte Carlo法脚蹬强度可靠性分析过程如图2所示,首先建立脚蹬的极限状态方程,然后根据随机输入变量的概率密度函数利用拉丁超立方法采取一定数量的样本,并对随机变量样本点进行循环分析,校验每次抽样结果是否满足极限状态方程,最后统计分析结果得到结构的失效率,进而获得脚蹬的可靠度。
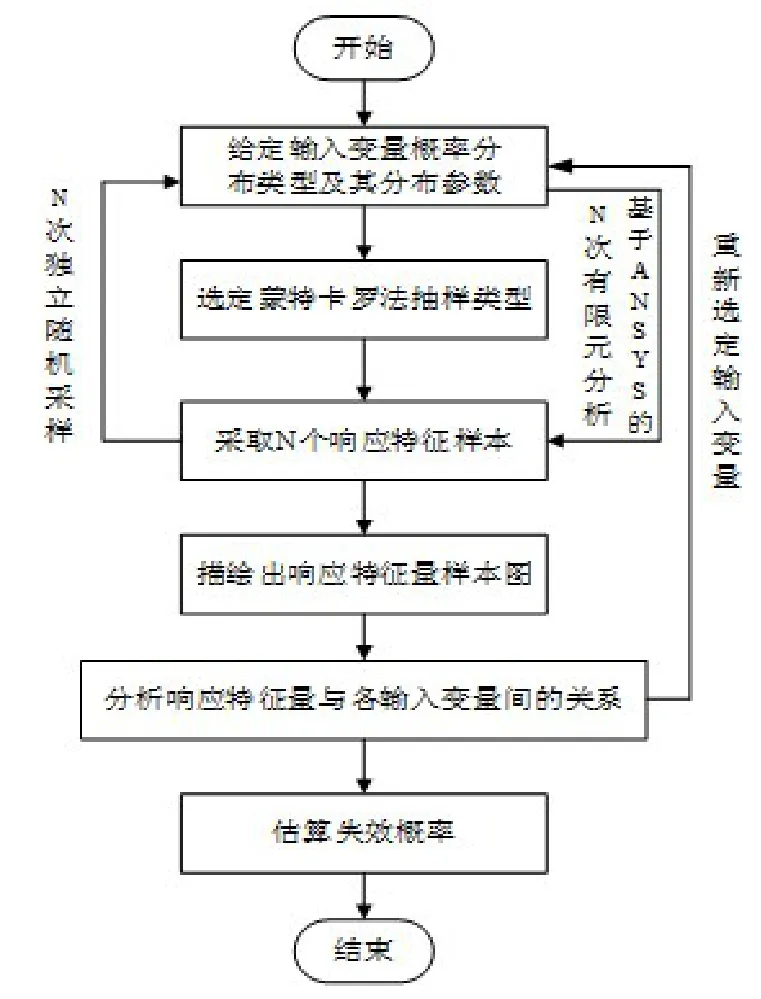
图2 脚蹬可靠性分析流程图
2.2 建立脚蹬有限元模型
根据脚蹬的承载特性,建立其有限元模型,如图3所示。脚蹬主要包括脚蹬主体、踏板、脚蹬框以及角铁,踏板由上至下分为三层,第一层踏板与脚蹬主体通过角铁螺栓相连,第二层、第三层踏板以及脚蹬框与脚蹬主体采用刚性元(rbe2)连接。脚蹬整体采用四边形壳单元模拟,单元基本大小为14mm,单元总数2 000个,节点总数2 224个。角铁所使用的材料为Q345钢,其余结构均采用Q235-B钢,弹性模量E=210GPa,泊松比v=0.274,屈服强度σs=235MPa。

图3 脚蹬的有限元模型
2.3 脚蹬的有限元分析
根据脚蹬的实际使用情况,按照IEC 61373-2010标准计算其所承受的工作载荷。对脚蹬框的上表层施加X、Y、Z方向的全位移约束,对第一层踏面螺栓刚性连接处施加X、Y、Z方向的全位移约束,如图4所示。

图4 脚蹬的工况加载
脚蹬踏板的强度校核根据工作条件共施加4个外力载荷。工况1为2kN的正交负载应用在第一层踏面的100×75区域,方向为-z,如图4所示;工况2为2kN的正交负载应用在第二层踏面的200×75区域,方向为-z;工况3为2kN的正交负载应用在第三层踏面的100×75区域,方向为-z;工况4为2kN的正交负载应用在第三层踏面的100×75区域,方向为+y。各工况下脚蹬的静强度仿真计算结果如图5所示。

图5 各工况脚蹬的等效节点应力云图
应用Von.Mises准则[8]进行脚蹬的强度校核,节点等效应力为

式中:σeq为节点等效应力;σi(i=1,2,3)为对应节点主应力。材料满足强度要求的条件是:σeq≤[σ]。
2.4 确定随机输入变量和结构功能函数
根据脚蹬的静强度计算结果,选定工况①作为强度可靠性分析时的超常载荷,以工况①的最大Von.Mises应力作为结构性能响应,设为SMAX,考虑与其相关的不确定性因素作为随机输入变量,主要包括材料属性以及结构板厚大小,见表1。

表1 随机输入变量
考虑以上不确定性因素对结构强度的影响,以脚蹬在超常载荷下的许用应力大于材料的最大Von.Mises应力为失效判据[9],根据此失效判据以及式(2)建立脚蹬的强度功能函数

式中:SMAX为超常载荷下脚蹬的最大Von.Mises应力,当Z0时脚蹬结构发生强度失效。
2.5 强度可靠性分析结果后处理
采用基于拉丁超立方采样的Monte-Carlo法对超常载荷下的脚蹬结构参数进行500次的抽样计算,得到优化前的可靠性分析结果。对于输出响应结果的评判,主要输出了极限状态函数值(Z)和脚蹬结构的最大Von.Mises应力值(SMAX)。图6为置信度为95%的Z和SMAX的历史样本抽样过程,置信区间上下限曲线表示500次抽样过程向均值曲线趋近的过程,通过观测输出变量的样本均值趋势曲线是否趋于稳定来判断抽样次数是否足够,以检验抽样次数能否满足精度的要求。
由图6可知,经过500次采样的Monte Carlo仿真循环后,极限状态函数曲线和最大Von.Mises应力曲线已逐步趋于平稳,说明500次仿真抽样已经足够,能够准确地进行脚蹬的结构可靠性计算分析。随着采样次数的增多,置信区间上下限宽度不断减小,Z的均值在2附近波动,大于0;应力均值收敛于202MPa左右,低于材料的屈服强度205MPa,最大应力处于190MPa和237MPa之间的样本频率相对较高,说明最大应力样本点落在190MPa和237MPa之间的数量较多。

图6 输出变量的样本均值趋势图

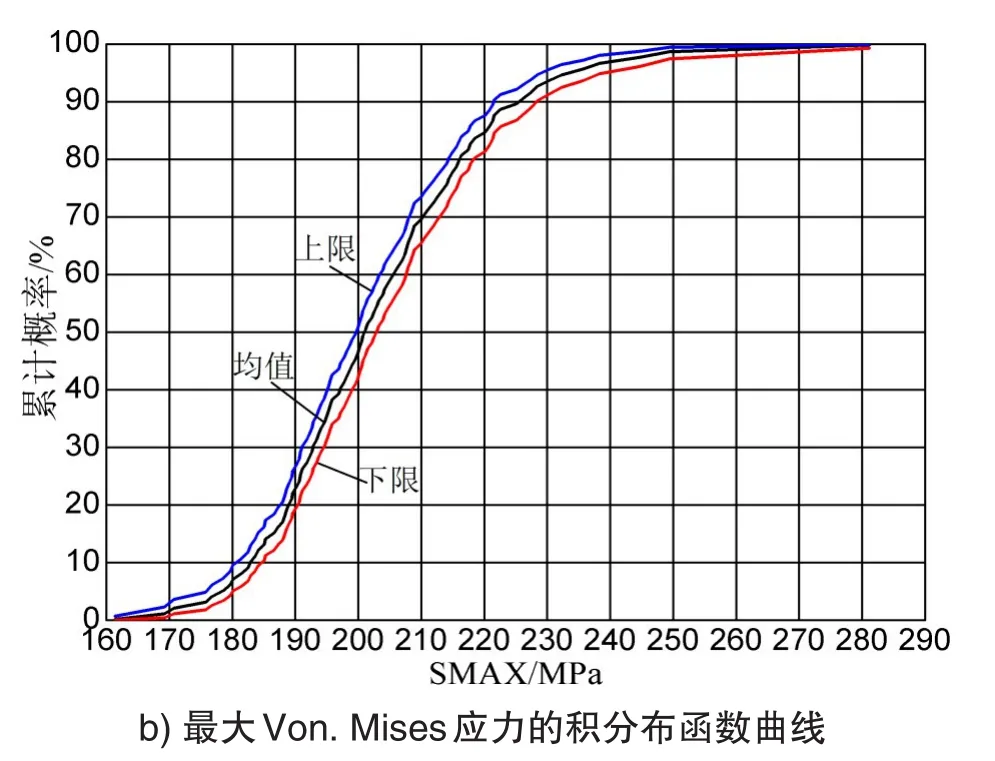
图7 输出变量的累积分布函数曲线
置信度[0 , 1]区间内,缺省值0.95,得到输出变量的累积分布函数曲线如图7所示。结合图8仿真总体功能函数Z的历史样本和可靠度结果图9可知,Z0的概率约为59.07%,即系统的可靠度为59.07%,失效概率为40.93%,失效概率较高,不满足可靠性设计要求。
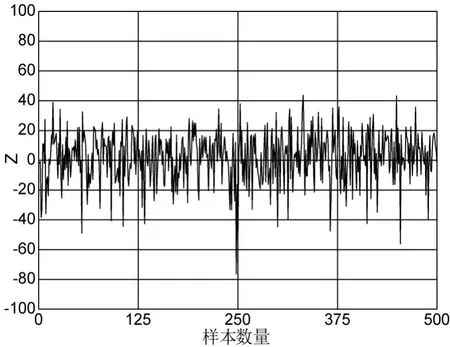
图8 Z的历史样本

图9 优化前Z>0的概率
3 脚蹬的尺寸优化
由脚蹬的强度可靠性分析结果发现其可靠性具有很大的优化空间,基于此,为了提高结构的力学性能,同时考虑轻量化也需要得到一定的保证,使用OptiStruct对脚蹬结构进行尺寸优化,以获得最佳的板厚组合。
Optistruct中,一个设计变量与其他设计变量之间的关系可以表示为[10]

式中:DDVID为该阶段最终的设计变量;C0为常量,本文取0;CMULT为常量系数,本文取1;IDVi为独立变量的标识;Ci为IDVi的系数。
选取角铁板厚、踏板板厚、脚蹬板厚以及脚蹬框的厚度共4个尺寸参数作为设计变量,以其在超常载荷工况(第①工况)下的加权柔度值最小化为目标函数,即脚蹬的总成刚度最大,以脚蹬总质量不超过优化前的质量为约束条件,建立尺寸优化数学模型

式中:Ti(i=1,2,3,4)为脚蹬各组成部件的厚度,W为加权柔度系数,本文取1,C为脚蹬在第一工况下的柔度值,M为脚蹬的质量。
经过迭代计算圆整得到尺寸优化后各板厚的最优解见表2。柔度目标函数迭代过程曲线如图10所示。

表2 尺寸优化结果

图10 尺寸优化目标函数柔度迭代曲线
对优化圆整后的脚蹬重新进行超常载荷下的静强度分析,应力分布如图11所示。尺寸优化前后脚蹬的力学性能对比见表3,圆整后的脚蹬在质量仅增加0.43kg的条件下,最大应力由优化前的200.78MPa下降到122.2MPa,减少39.1%,并且小于材料的许用应力;而最大变形量由优化前的2.45mm下降到0.76mm,减少69.1%。对优化圆整后的脚蹬结构采用基于拉丁超立方抽样的Monte-Carlo法进行500次的抽样计算得到最终的可靠度结果如图12所示,由优化前的59.07%提升到100%,优化后的脚蹬满足了可靠性设计要求,取得了较好的优化效果。
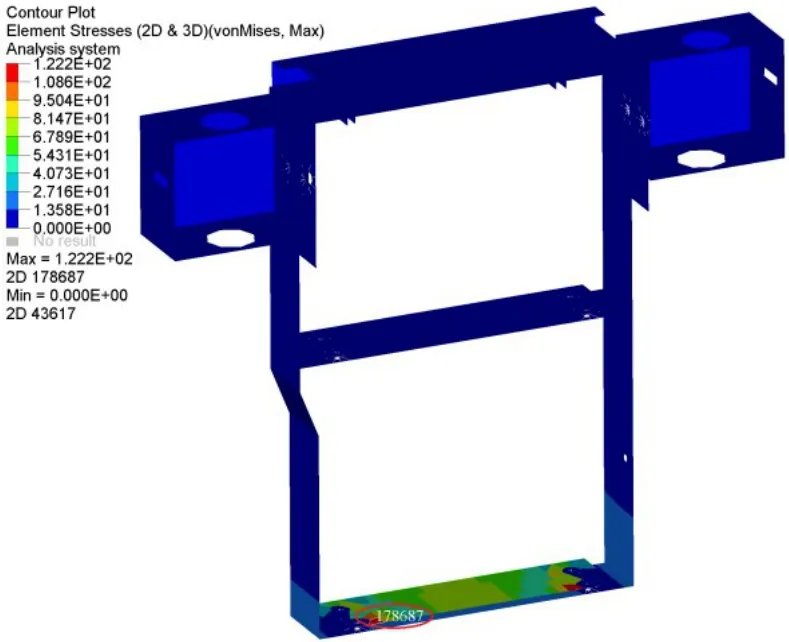
图11 优化圆整后脚蹬的应力云图

图12 优化后脚蹬结构可靠性分析结果
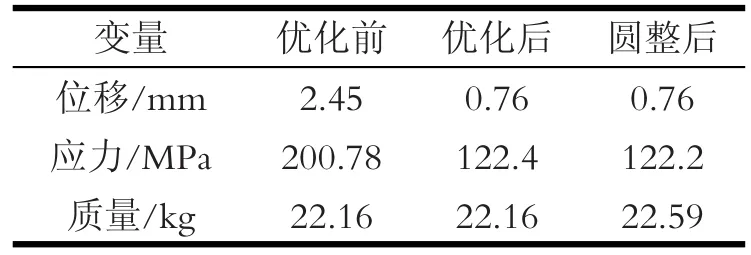
表3 优化前后对比
4 结语
①采用基于拉丁超立方采样的Monte Carlo法对某地铁车车头脚蹬进行超常载荷下的强度可靠性分析,经过500次抽样仿真分析后得到脚蹬的可靠度为59.07%,不满足可靠性设计要求。
②采用OptiStruct对脚蹬进行尺寸优化,优化圆整后的脚蹬在力学性能很大程度提高的前提下,其可靠度由优化前的59.07%提升到100%,达到较好的优化效果。
