“以题组为情境”的高三数学复习课应用——以“隐圆”为例

江苏省南通田家炳中学 易 峻

“以题组为情境”，即是把知识点、例题、技能与方法通过精心设计，变成一系列问题或题组，在发现问题、解决问题时强化和提升，从而达到课堂教学的效果。

一、问题的提出

在高三数学复习题中，一般会采用“知识回顾—题型总结—学生训练”的传统模式。这种模式对于高三的学生而言，司空见惯，难以激发学生的兴奋点，也就难以达到设计预期。造成这样结果的原因是多方面的：

首先，高三数学复习题的教学目标是基于清除学生的知识和方法盲点，同时有效地构造知识网络，进而有效灵活地运用数学思想和数学技能解决问题。而传统模式中的知识回顾和题型总结脱节，题型总结更是求全而体系化弱，无法对学生形成有效的刺激，造成了学生听听都会，应用时对不上号。

其次，美国缅因州国家训练实验室提出的学习金字塔，用量化的方式发现学生的主动学习（讨论、实践、教授他人）明显优于被动学习(听讲、阅读、视听、演示)的成果。传统复习课上的将知识、题型和练习的割裂使得学生的参与度低，演化成被动接受，不能主动建构体系并积极实践运用。

再次，基础知识点和基本技能可以看作数学核心素养的外在表现形式，在实际解题中，必须能体现数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析六大核心素养。以此促进数学知识的深刻理解和技能的提升。因此题型表面上的完整性无法深化学生自身的理解能力，对学生的数学能力的提高无实际帮助。

下面将以“隐圆”为例，探索题组为情境，融合知识点、方法和例题的可行性和功能性。

二、课堂实录

1.知识回顾环节

教师：怎么求？

学生2：存在P点在直线x-y+m=0上且满足x2+y2=4，即转化为直线与圆有公共点，从而利用d＜求解。

题组一：2.在平面直角坐标系中，圆C：x2+y2-4x=0，以及点A(-1，0)，B(1，).在圆C 上是否存在点P，使得PA2+PB2=12？若存在，求点P 的个数；若不存在，说明理由。

学生3：基于PA2+PB2=12 关系，A 为定点，P 为动点，求出P 点轨迹为x2+y2=5，进而转化为圆与圆的位置关系求解。

教师：有些数学问题，将圆隐藏在已知条件里，隐晦地考查，解题时，需要我们通过分析探索，发现这些隐藏的圆（简称隐圆）。你能归纳出常见的隐圆类型吗？

学生4：A 为定点，P 为动点，型如：PA=λPB、PA2+PB2=λ、PA÷ PB=λ。

学生5：当将隐圆的动点轨迹转化圆时，就可以使用点和圆、直线和圆、圆和圆的位置关系来解题。

在整个知识回顾环节，教师通过题给创设情境，学生在探索中归纳知识，发现隐圆的转化条件和一般解题思路，教师是组织者、参与者，但学生主体性地位和知识体系、方法体系均被强化了。

2.例题教学

题组二：1.在平面直角坐标系xOy中，设点A(1，0)，B(3，0)，C(0，a)，D(0，a+2)，若存在点P，使得PA=PB，PC=PD，则实数a 的取值范围是？

学生6：转化为直线与圆的位置关系解决。

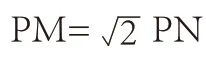
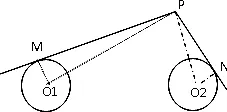
学生7：将切线长PM、P 转化P1和P2表示，再次转化为两定点、一动点问题求P 点轨迹(x-62+y2)=3。

教师：这是化归的思想。本节课通过题组一的研究，抽象出隐圆常见的三种形态，推理出转化为轨迹相交的问题，建立起点与圆、直线与圆、圆与圆位置关系的模型，结合解析几何中图形的直观性解决问题，解题过程中应注意计算能力的培养，会对数据进行分析。

3.课后练习

题组三：1.在平面直角坐标系xOy中，已知圆C：(x-a)2+(y-a+2)2=1，点A(0，2)，若圆C 上存在点M，满足MA2+MO2=10，则a 的取值范围是__。

题组三：2.在等腰ΔABC 中，已知AB=AC，B(-1，0)，AC 边的中点为D(2，0)，点A 的轨迹所包围的图形的面积等于____。

通过构造层层递进的题组，将直观向深层次推进，分解教学难点，加深学生对隐圆问题处理的一般化方法的理解，并在深化中收获成功，从而提升学生数学的核心素养。

三、思考与实践

知识是理论，运用是实践，只有理论与实践的完美融合才会成为学生学习的动力源泉。学生学习的主观性是学习进步的推动力，而主观性又必须得到教师的保护和鼓励。学生自主发现的知识点是高效且高质量的，这将成为向上蹦一蹦的基础，通过题组就夯实了这一基础，也就保护学生进一步学习的动力和能力。

数学的学习不应该是平面的，而是向着思维的纵深处去发展。题组中采用一题多变、一题多解等设计有助于学生网络化地建构数学体系，有效地克服急功近利的题海战术，进而提升学生的核心素养。