基于经纬网格的点云孔洞填补算法

李由之, 唐志荣, 刘明哲

(1.成都理工大学核技术与自动化工程学院,成都 610059；2.成都理工大学地质灾害防治与地质环境保护国家重点实验室,成都 610059)

在点云数据采集过程中,因被遮挡、表面反射、技术限制等因素影响,不可避免地出现点云数据缺失现象,从而产生不利于后续数据处理的孔洞区域,因此,必须先进行包括排除干扰数据、数据简化、目标识别、点云配准和对孔洞进行修复。该过程主要有两个难点:①怎样尽可能精确地获取孔洞边界；②怎样获取更多孔洞区域的信息,从而使修补接近原始形状。

雷敏等[1]提出使用包围盒算法对点云数据进行过分聚类,并通过中心点代替过分簇后进行基于密度的再聚类来达到简化点云数据的目的。杨飚等[2]提出先用正态分布变换(normal distributions transform,NDT)算法进行粗配准,再用迭代就近点(iterative closest point,ICP)算法进行微调和精确配准的点云配准法。此类方法或适用于孔洞修复前的识别与配准。

文献[3]提出插值法对孔洞进行填补,对于曲率变化较大或者形状较为复杂的孔洞区域。文献[4-5]通过缩短孔的边缘流动和分段法等方法进行孔洞修补。Pernot等[6]提出根据孔洞最小邻域和插入网格之间的曲率变化进行孔洞修复。文献[7-9]通过重建函数、计算传热参数、几何信息和图像信息等方法修补孔洞。

Marchandis等[10]提出以初始网格为基础,使用径向基函数计算离散参数重构初始网格实现孔洞的修复。Yumer等[11]提出基于神经网络的孔洞修补算法。Quinsat等[12]提出利用网格变形的方法来填充数字化点云中的孔。Centin等[13]提出利用泊松方程完成三角形网格无缝修补。Yang等[14]提出形状可控的点云几何模型重构算法,能够在光滑模型或具有尖锐特征的表面上修补孔洞。Zhong等[15]将空间域转化为其他域或数学模型以到达修补孔洞的目的。

Jun[16]将复杂的孔洞依据孔洞边界的三维形状分成几个简单的孔洞,然后用平面三角测量法连续地填充每个离散的简单孔洞直到整个填充完毕。Kanle等[17]针对圆形孔洞提出了基于四边形分割和约束优化的方法,对指定的圆形孔洞边界进行重新参数化,以确保相邻边界增长点在连接点上的相容性,方法简单高效且无需迭代或大规模矩阵求解。Wang等[18]对于具有阴影信息的点云模型,利用最小二乘法内插几何信息,可以同时内插几何和阴影信息。

张琦等[19]提出了一种基于改进的曲线收缩流虚拟修补点云张开孔洞的方法,利用孔洞边界点的表面法向量和切向量对孔洞进行修补。曾露露等[20]提出一种基于从运动中恢复结构的三维点云孔洞修补算法,利用光栅投影法中得到的二维相位信息来提取三维点云孔洞区域的边界点从而完成对点云孔洞的填补。文献[21]提出的轮廓提取,或许可以用以辅助解决此类问题。

为解决三维点云数据存在的复杂孔洞区域且难以搜索孔洞位置对后续处理造成影响的问题,提出一种基于经纬网格的点云修补算法。实验证明,比起传统修补方法,该算法具有更好的鲁棒性,从而更好完成对复杂孔洞的修补以便进行后续重建处理等过程。

1 点云孔洞修补

1.1 坐标转换

将给定点云A={a1,a2,…,aK},(ai={xi,yi,zi}T)转化到球坐标下：

(1)

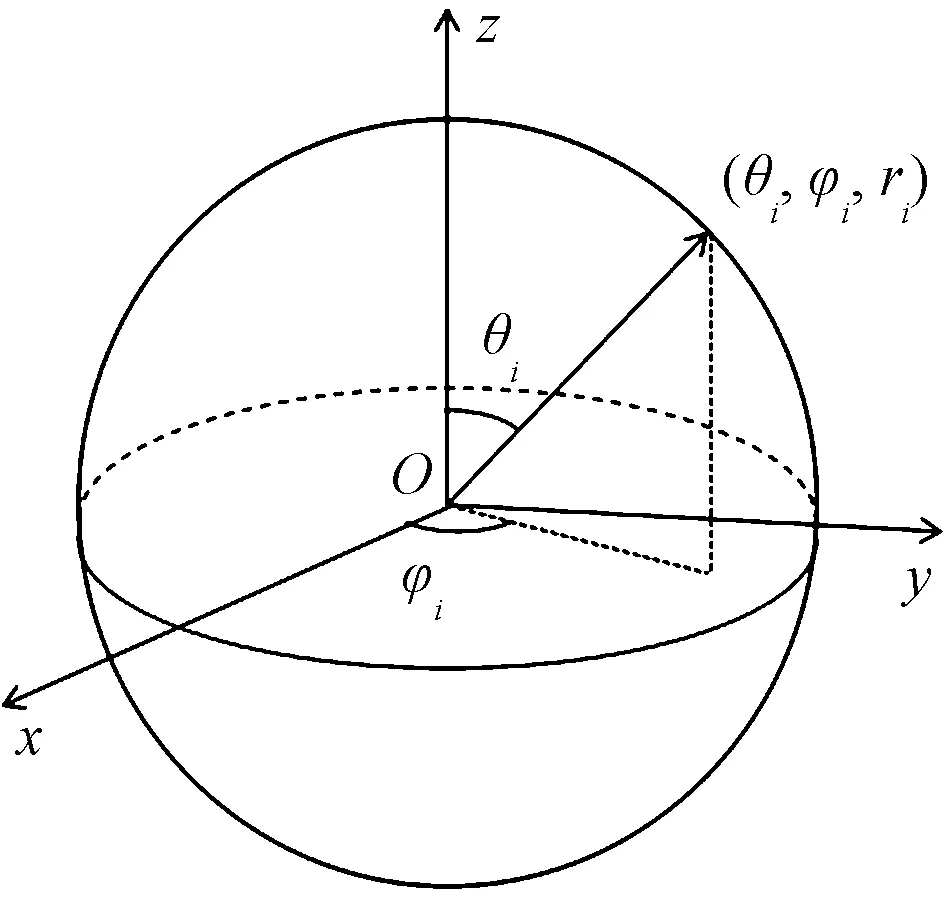
图1 三维球坐标Fig.1 3D spherical coordinates

得到球坐标点云：

Q={q1,q2,…,qK}

(2)

式(2)中：qi={θi,φi,ri}T,i=1,2,…,K表示球坐标下的点。

1.2 经纬网格区域划分和点集选择

采用经纬网对球坐标点云Q进行划分,设有M条经线,N条纬线,则可以将球体划分为

Aarea=2MN

(3)

个区域，每一块区域的角度间隔为

(4)

每一块区域可表示为

Aarea(m,n)={(mΔθ,nΔφ),[(m+1)Δθ, (n+1)Δφ]}

n=1,2,…,N-1;m=1,2,…,M-1

(5)

第(m,n)块区域点集的选取满足以下关系：

(6)

式(6)中：O表示区域(m,n)中点的数量。并得到相应球坐标下角度坐标集合：

(7)

1.3 寻找孔洞并修补

采用蒙特卡罗方法求取每块区域点的平均密度。对(m,n)区域生成一个样本数据集：

Ssample(m,n)={s1,s2,…st,…,sλ×O}

(8)

式(8)中：λ∈N+表示样本点数与原点数的比例倍数；st={θt,φt}∈R2×1。满足：

(9)

选取(m,n)区域内的阈值半径：

(10)

(11)

将Ssample(m,n)中满足：

L(t,o)≤r(m,n)

(12)

的S个点选取出来组成新样本集：

(13)

计算(m,n)区域内点的密度：

(14)

设定一个阈值ε>0,满足：

ρ(m,n)<ε

(15)

为有孔洞区域。寻找孔洞C个邻域的Sample点集如图2所示。

图2 C个邻域的样本点集Fig.2 Sample point set of C neighborhoods

组成新的样本点集：

C={c1,c2,…,cC}

(16)

并计算出邻域内样本的平均点个数和密度：

(17)

对点集C形成的复杂的空间曲面在其局部面元可以利用一个简单的二次曲面：

ri=f(θi,φi)

(18)

去逼近拟合表达;当局部面元小到一定程度甚至可以将其近似地表达成一个平面。这里采用双线性插值算法对曲面进行插值,取

(19)

式(19)中:[θn]表示不超过θn的最大整数；[φm]表示不超过φm的最大整数。首先由f(θ,φ)、f(θ+Δθ,φ)对θn插值：

f(θn,φ)=f(θ,φ)+α[f(θ+Δθ,φ)-f(θ,φ)]

(20)

然后,由f(θ,φ+Δφ)、f(θ+Δθ,φ+Δφ)对φm插值：

f(θn,φ+Δφ)=f(θ,φ+Δφ)+α[f(θ+Δθ,φ+Δφ)-f(θ,φ)]

(21)

最后,由(θn,φ)、(θn,φ+Δφ)做第三次垂直方向的插值计算：

f(θn,φm)=f(θn,φ)+β[f(θn,φ+Δφ)-f(θn,φ)]=f(θ,φ)(1-α)(1-β)+f(θ+Δθ,φ)α(1-β)+f(θ,φ+Δφ)(1-α)β+f(θ+Δθ,φ+Δφ)αβ

(22)

插值点的个数为

(23)

将插值得到的点集转化为三维坐标即可。本文算法流程如下。

经纬网格法:输入为存在孔洞的点云A；输出为对孔洞填补后的点云A。

(1)通过式(1)将点云转为球坐标Q。

(2)根据式(4)～式(5)对球坐标Q进行区域划分,根据式(7)得到每个区域内的点集。

(3)由式(8)、式(9)生成对应样本点。

(4)通过式(10)～式(15)求出孔洞区域。

(5)根据式(16)～式(23)对孔洞进行填补。

2 实验分析

采用Stanford大学提供的Bunny(31607)三维点云数据进行仿真试验。实验是在MATLAB 2017a版本、i7-6700HQ四核处理器和GTX965M下进行的。经过实验,取N=40,M=40,ε=0.1能够准确搜寻出所有孔洞位置。

2.1 孔洞修补

在实际扫描数据的过程中,由于被扫描物体的表面反光或操作不当,会造成点云表面存在孔洞的现象。为了验证本文算法对点云孔洞具有有效的填补能力,故对点云进行人工处理,扣掉一部分,再利用本文算法找出孔洞进行填补,状态如图3所示。

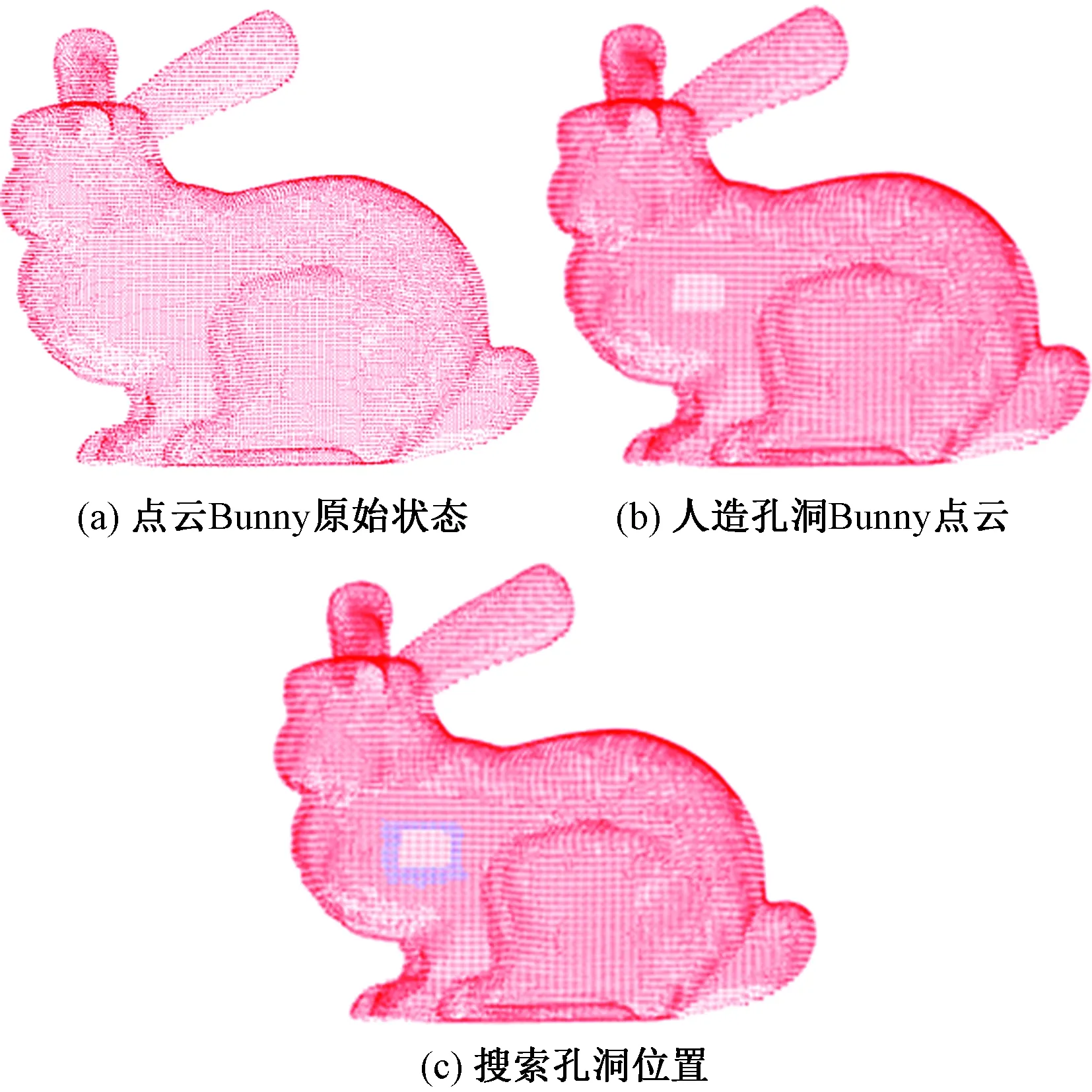
图3 点云Bunny状态Fig.3 Shows the Bunny state of the cloud

从图3可以看出,将原始Bunny点云,如图3(a)所示,经过人工处理后,扣出了一个方形的孔洞如图3(b)所示。图3(c)表明本文算法能准确地找出点云孔洞的位置,以及孔洞邻域内的点集。

2.2 效果对比

利用本文算法、文献[20]算法、文献[21]算法修补后的效果如图4所示。

图4 3种算法修补效果Fig.4 Three algorithm patching effects

将本文算法与文献[20]、文献[21]的算法填补状态和填补点数进行对比,如表1所示。

表1 不同算法区域内点数及填补时间对比

图4中不同颜色代表不同算法对孔洞的填补状态。从图4可以看出,本文算法的填补状态最好,能最大程度地填满孔洞,而文献[20]算法对孔洞的填补并不完全,文献[21]算法对孔洞填补的过多。从表1可以看出,本文算法对Bunny点云填补后的点数与原始点云数据的点数相差不大且填补时间最短,文献[20]算法虽然效率快但比源点云数据少,文献[21]算法时间最长且比源点云数据多。可见本文算法能较好地补全缺失孔洞的点数,填补的点云数据和原始形状完全贴合,并能准确地描述原始细节。

3 实物孔洞填补

为验证本文算法的实用性,利用HandySCAN 700 三维激光扫描仪获取一组实物心形点云数据,初始状态如图5所示。

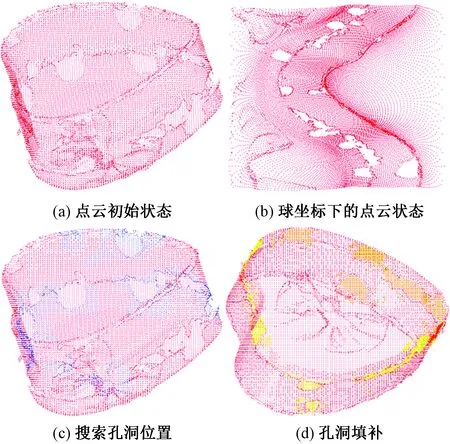
图5 心形点云状态Fig.5 The state of centroid point clouds

从图5(a)中可以看出,实际扫描出的点云数据由于物体表面反光等原因,存在许多孔洞,且分布不规则,具有随意性。利用本文算法,把直角坐标系下的点云转换成球坐标形式,如图5(b)所示,可以清晰地看出,所有的孔洞均位于同一曲面上,这样便能准确地搜索出每一个孔洞的位置,且能更为精确地提取孔洞信息,如图5(c)中蓝色部分所示(由于软件自身原因,部分区域未显示出来)。再利用插值算法对搜索到的孔洞进行填补,可以有效地对点云数据进行修补,修补结果如图5(d)中黄色部分所示。对填补前后点云的点数进行对比，如表2所示。

表2 区域内点数及填补时间

从表2可以看出填补前后,数据增加了1912个点,而算法时间只用了28 s,本文算法的修补效率也较快。

4 结论

针对三维点云数据存在孔洞区域、对后续处理造成影响的问题，提出一种基于经纬网格的点云修补算法。从实验结果可以得到，该算法能较为有效地恢复复杂物体的表面信息。比起传统修补方法，本文算法能准确提取孔洞信息，较好地补全缺失孔洞的点数，填补的点云数据和原始形状完全贴合，并能准确地描述原始细节。且用时较短，并具有更好的鲁棒性，从而更好完成对复杂孔洞的修补以便进行后续重建处理等过程。