基于朴素贝叶斯分类器的乘客出行属性分析

崔洪军, 赵 锐, 朱敏清, 李 霞

(河北工业大学土木与交通学院，天津 300401)

智能卡的广泛应用在各大城市中产生了海量的乘客出行信息数据，充分利用这些数据中的出行属性可有效地分析乘客的出行特征、规律等[1-2]。Atfred等[3]、Ma等[4]利用时空关联理论分别分析了智能卡乘客在指定车站的乘降数量及关联行程，针对北京智能卡出行者的出行时空特性规律进行了研究。Kusakabe等[5]对地铁出行乘客的智能卡数据加以研究进而得到出行者的出行规律信息。Ordóez等[6]对出行活动进行聚类，并利用分层选择模型对为期7 d的连续出行活动进行了分析。Sang等[7]、Gordon等[8]、Nassir等[9]。基于公交智能卡数据对出行目的、出行链等进行了分析。王月玥[10]、翁剑成等[11]对通勤者的出行特征属性及出行链进行了提取。呙娟[12]基于时空关联理论，结合个体出行特征对乘客的出行规律进行了一定分析。刘永鑫[13]、Weng等[14]、Liu等[15]基于智能卡数据，对乘客的出行模式进行了深入研究。

从以上成果可看出，学者多注重于从单一数据源来分析乘客的出行规律，但如将多源数据融合，研究结果将会更准确及多元化。同时，以上诸多研究侧重于对地铁乘客出行规律的推断；在出行选择繁多的今天，传统的公交出行依旧拥有很大的研究价值。在多数城市，公交出行的计费方式等与地铁存在差异，因此在智能卡数据库中会缺失部分出行属性信息。鉴于以往研究中的不足之处，基于朴素贝叶斯分类器，融合了出行调查数据及智能卡数据对公交乘客的出行目的进行推断，并基于各出行目的对出行规律进行研究。

1 研究数据描述

1.1 智能卡数据预处理

研究数据来源为石家庄市公交智能卡及公交全球定位系统(global positioning system, GPS)数据，其中智能卡基础数据为数据卡ID编号、刷卡时间、车辆号、车辆线路号等，GPS数据包括车辆终端号(车辆号)、GPS时间、经纬度数据、GPS接收时间等。由于篇幅限制，只选取研究所需数据，数据结构如表1所示。

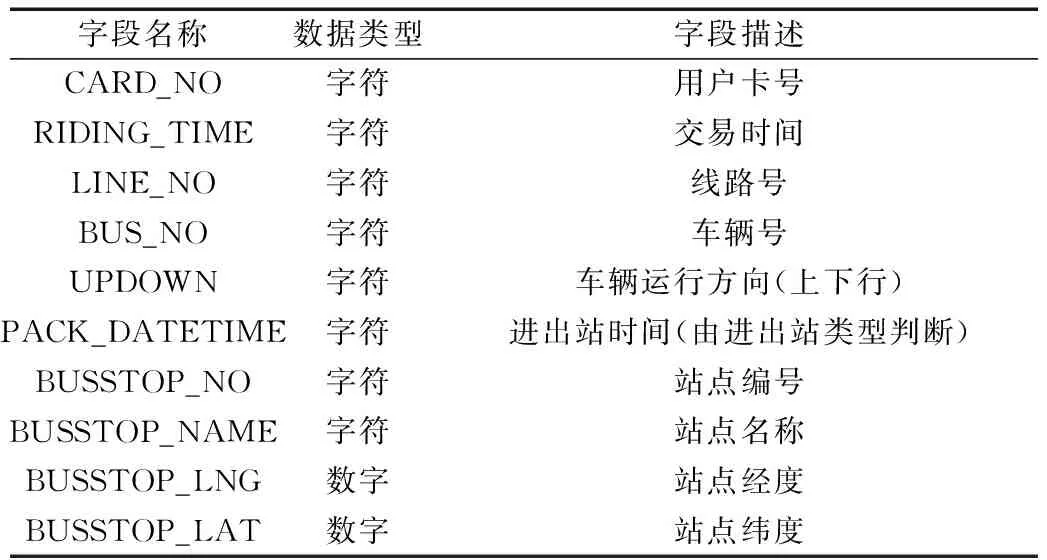
表1 智能卡数据描述

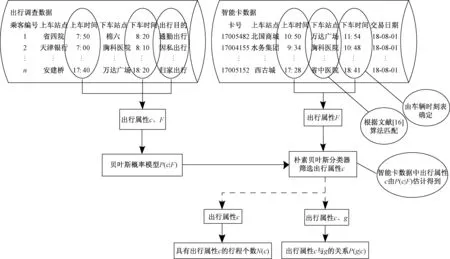
图1 数据融合算法流程Fig.1 The flow of data fusion algorithm

通过匹配智能卡刷卡时间与车载GPS进站时间可确定乘客的上车站点信息。由于石家庄公交系统采用一票制刷卡乘车原则，乘客的下车站点数据信息无法通过系统自动获得，因此选取文献[16]中的方法匹配下车站点数据，并且通过车辆时刻表确定乘客的下车时间节点。

1.2 出行调查数据

采用问卷调查的方式获取公交乘客的出行信息，调查背景为限定的一个乘降站。调查内容包括乘客出行的上下车站点、上下车时间及出行目的。出行调查数据如表2所示。

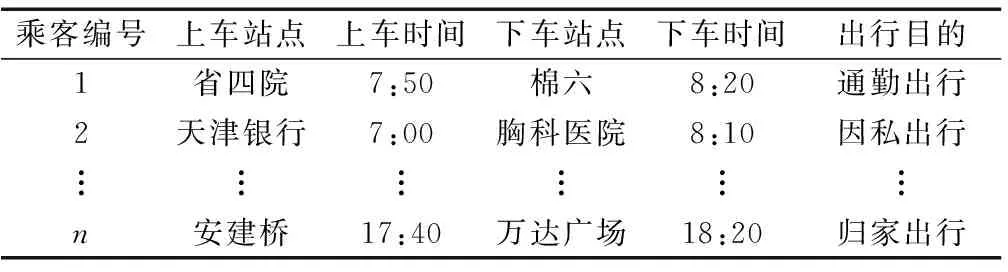
表2 出行调查数据

2 数据融合算法

2.1 方法概述

提出一种同时结合出行调查与智能卡数据的数据融合方法，依照此方法可将公交智能卡数据中缺少的乘客相关属性信息进行提取。图1所示为该方法的流程，此法核心为推断智能卡乘客的出行行为属性。乘客的出行行为属性c(如出行目的、起始地)为仅在问卷调查中得到的属性；属性F(如上车站点和上车时间)为两个数据集中均包含的出行属性，属性g为仅从智能卡数据集中获得的属性(如出行频率)。基于该方法，使计算智能卡数据集中具备属性c的出行次数成为可能；同时，也得到了无法在单个数据集中得到的属性c和g的关系。

假设从智能卡数据集中观测到的乘客出行次数同问卷调查数据集中得到的乘客出行次数具有相同的条件概率分布函数P(c|F)，此分布表示该乘客在属性F条件下产生出行属性c的概率。将概率函数P(c|F)应用到朴素贝叶斯分类器中，可将智能卡数据集中的出行属性c提取出来，基于此可得到各出行属性下的概率分布关系。同时，N(c)为具有出行属性c的出行次数，属性c和g的关系可用当c已知时g的条件概率分布P(g|c)来表示。

2.2 朴素贝叶斯概率模型

假设向量集F={f1,f2,…,fk}为一系列行为属性，F中的每个元素均代表着两个数据集中存在的一个共有属性(如上车时间、上车站点)。c为可通过问卷调查获得的智能卡数据集中缺失的属性变量。将c及集合F中的每个元素视为离散变量，基于贝叶斯定理，概率P(c|F)可表示为

(1)

式(1)中：p(c)、p(F)、p(fk|c)均为从问卷调查中获得的概率分布；p(c)、p(F)分别为出行中具备属性c和F的概率，条件概率p(fk|c)为在属性c下，具备属性fk的出行所发生的概率。

当智能卡数据集中每次行程的属性F被观测确定后，由朴素贝叶斯分类器可得到该行程的出行属性c，表达式如式(2)所示，其中，C为所有出行属性c的集合。同时，可由式(3)得到此出行属性下的行程次数，其中S为所有F取值集合。

(2)

(3)

当问卷调查数据集中的属性变量g在智能卡数据集中被计算出后，属性g与属性c的联合概率分布可由贝叶斯推理得出，即

(4)

式(4)中：ps(F,g)为从智能卡数据集中得到的具有出行属性F和g的行程占比。通过出行调查数据及智能卡数据可得到在属性c下属性g的分布条件概率：

(5)

式(5)中：ps(F)为由智能卡数据集中得到的具有属性F的出行占有率。

2.3 出行目的推测

为推测智能卡乘客的出行目的，将出行目的定义为2.2节中所述的属性c，如式(6)所示。其在出行问卷调查中的意义如下：其中通勤出行包含成人上班、学生上学出行；因私出行包括出行人以休闲、购物、探亲、访友、商务会见等为目的的出行；归家出行包括除通勤返程以外的归程出行。同时定义特征属性g为依据智能卡出行数据求得的乘客的出行频率。

c∈{通勤出行，因私出行，归家出行}

(6)

假设乘客的上车时间、出行持续时间、目的地、出行逗留时间等各出行特征参数均因出行目的而异。基于此假设，两个数据集中共有的出行属性F定义为F={faboard,fduration}，其中faboard为乘客上车刷卡时间节点，fduration为乘客出行时下车后又在同一车站刷卡上车的时间间隔时长，在研究中称此为活动持续时间。至此，由上述方法可得到智能卡数据库中缺失的乘客出行目的属性。

3 实证分析

3.1 数据准备

选取石家庄CBD中心区北国商城公交站为研究对象，周边办公写字楼、宾馆、酒店、医院、购物中心齐全，有较大的客流量；同时存在多种目的的出行需求。公交智能卡数据为2018年1月1日至2018年3月25日期间的交易数据。经筛选处理后北国商城站的可用出行数据共计199 145条，其中包含卡号10 263个，所用数据中保证了出行者至少出行一次。出行调查采取问卷调查方式，针对本文研究站点，可用问卷共计1 000份，将其随机分为两部分，其一用于推算概率分布P(c|F)，共计700份，余下300份用于检验其准确性。

3.2 概率估算结果

700份问卷样本数据结果通过式(1)的概率模型计算。概率分布结果P(c|F)由出行属性F={faboard,fduration}决定，因此，模型的准确程度取决于所选属性集合F能否合理地体现乘客的出行目的。同时，朴素贝叶斯分类器假定各元素服从有条件的独立分布，因此，P(faboard|c)与P(fduration|c)两个分布情况被分别加以计算。

表3及表4分别展示了700组问卷数据在上述两种分布情况下的计算结果。由此可看出，通勤出行多集中在早间高峰时期，同时逗留时间也远长于因私出行的逗留时间，归家出行集中在下午5时以后，符合日常规律。

3.3 算法验证

为验证本文聚类方法的准确性，笔者利用前文所述的300组包含出行属性F和c的出行调查数据来检验，通过比较推测出行目的与实际出行目的来判断由式(2)推断出的结果的准确性。图2所示为

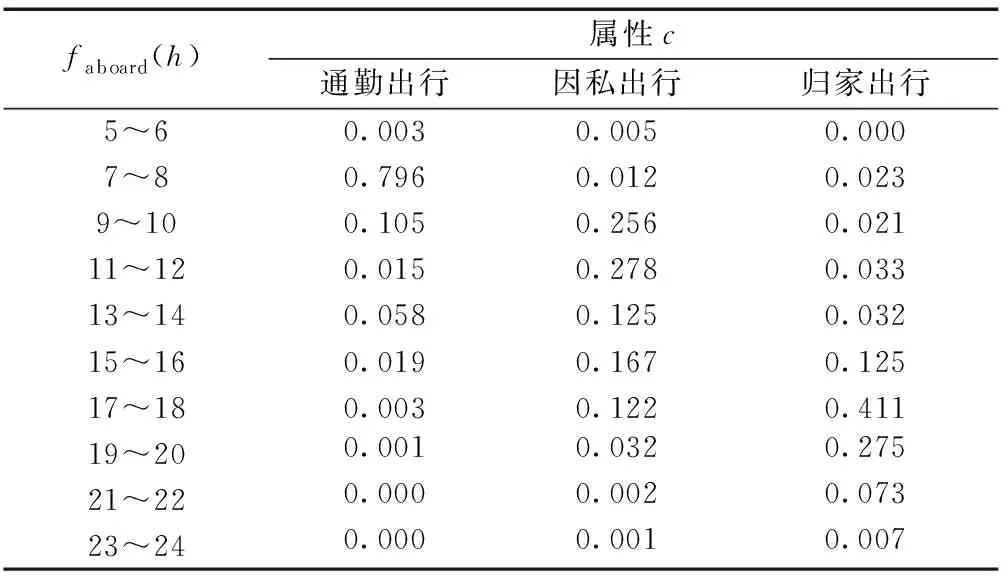
表3 北国商城站出行调查概率p(faboard|c)的分布值

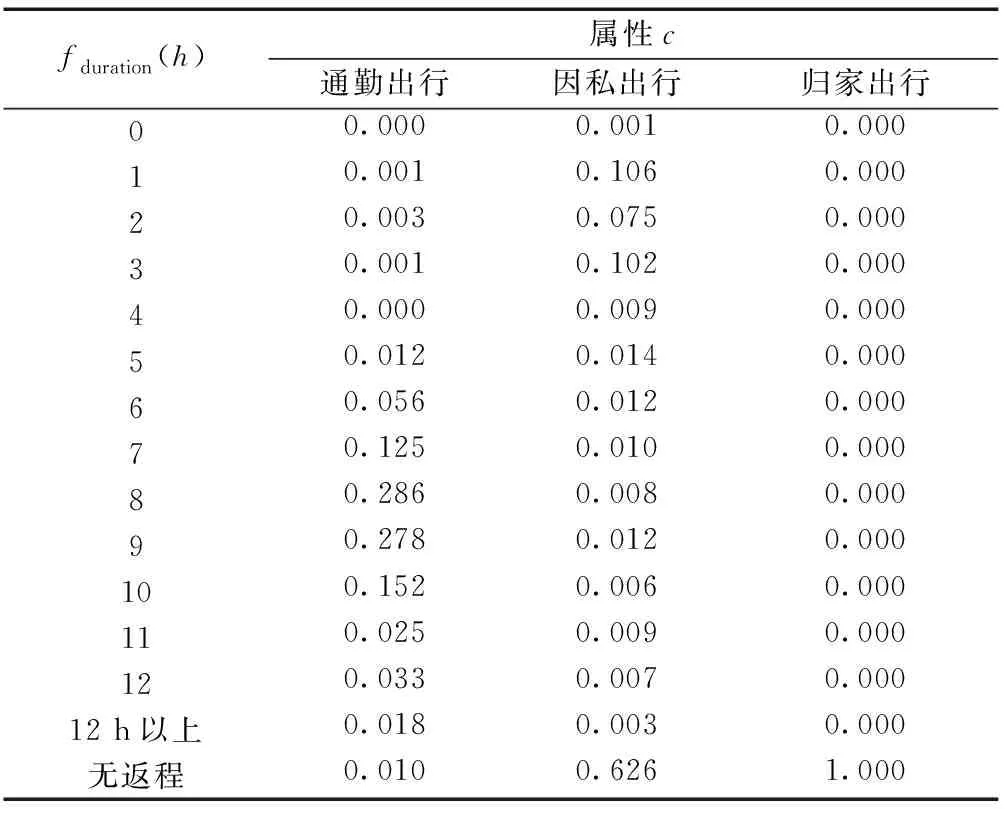
表4 北国商城站出行调查概率p(fduration|c)的分布值

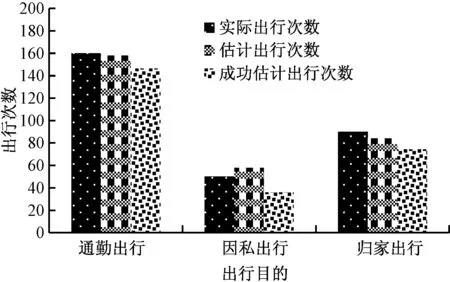
图2 北国商城站以出行目的聚类的出行次数统计Fig.2 Number of trips at Beiguoshangcheng station counted by trip purposes

由式(2)、式(3)得到的结果分布情况。其中，85.6%的出行被准确估计，通勤出行、因私出行、归家出行的准确性分别为91.5%、72.1%和82.6%。

3.4 智能卡数据分析

为了分析乘客在不同时段的出行行为变化情况，基于上述数据融合方法对智能卡数据进行分析。由式(3)统计后可得到图3所示的2018年1月1日至2018年3月25日北国商城站为期12周的乘客日出行频次变化情况。

图3 北国商城站出行量日变图Fig.3 Daily variation of travel volume at Beiguo-shangcheng station

由图3可看出：该车站工作日期间日出行量稍有波动，其中通勤出行占比最大，归家出行稍高于因私出行；但在周末及假日期间，通勤出行占比明显减少，归家出行成为主要出行目的，且稍高于因私出行；工作日与周末衔接处可见显著波动。同时，值得注意的是2月15日至2月21日春节假期期间本站的出行变化情况：此时段较前后时段相比，日出行数量显著减少，主要以归家出行为主，伴有少量因私出行及通勤出行。该站春节假期前后工作日时段通勤出行、因私出行、归家出行的日出行量均值分别为1 598、407、509次；周末时段日出行量均值分别为706、777、959次；而在春节假期期间，以上出行目的下的日出行量均值则分别为60、146、451次。

图4所示为由式(5)得到的研究时段内通勤、因私、归家各出行目的下的出行频率。图中横轴为研究时段，纵轴为该站点每周内每名乘客的出行次数，不同色块代表不同时段中每名乘客在该站点的出行次数占比情况。由图可知，乘客通勤出行平均每周4.7次，因私出行每周2.9次，归家出行每周3.4次。由图4(a)可知，在第7、8观察周(春节假期)中，每名乘客的通勤周出行次数多为3次；参考图4(b)、图4(c)可知，该时期每名乘客的因私出行次数明显上升，且多集中于5次，而归家出行次数在前半段春节假期中较平时上升明显，在后半段中则与平时相差不大。

图4 北国商城站不同出行目的下乘客出行次数周变频率Fig.4 Weekly frequency chart of passenger trips for different purposes in BeiGuo Shang Cheng STA

4 结论

提出了一种数据融合方法。此法基于朴素贝叶斯分类器，通过融合智能卡及出行调查数据，结合公交智能卡乘客出行属性F(上下车时间及活动持续时间)对出行目的加以分类。基于不同的出行目的，将乘客的出行频率加以描述，以此刻画乘客的出行行为，验证表明该法对出行目的估计的准确率为85.6%，其中通勤出行、因私出行、归家出行的准确性分别为91.5%、72.1%和82.6%。

基于不同的出行目的对所研究时段的刷卡数据进行分类。结果表明，该方法能够有效地筛选出不同出行目的下智能卡乘客的出行频率，同时可阶段性地刻画乘客的出行偏好。基于本研究选取车站，得到了2018年春节假期前后各出行目的下的出行变化规律、日出行量均值及乘客出行次数周变规律。结果可为交通规划部门提供较好的信息支撑。