基于足尺模型试验的边坡裂隙发展演化规律

2020-06-04张家铭罗易周峙CHIKHOTKINVictor袁超王少锋

中南大学学报(自然科学版) 2020年4期

张家铭，罗易，周峙，CHIKHOTKIN Victor，袁超，王少锋

(1. 中国地质大学工程学院，湖北武汉，430074；2. 安徽省交通控股集团有限公司，安徽合肥，230088)

随着长江经济带发展战略规划的实施，沿江地区高速公路建设日益增多。在安徽沿江地区高速公路建设中，灰白色裂土边坡频繁出现失稳破坏，并带来了巨大的安全隐患和经济损失。现场调查及监测结果表明，裂隙是导致区内边坡失稳破坏的根本原因，查明裂隙在边坡失稳破坏过程中的演化律，对于减轻该类特殊性岩土边坡灾害有较强的科学意义和工程价值。研究土体裂隙的试验方法主要有单元试验与现场试验。如SHORLIN等[1-16]，开展的单元试验大多利用数码照相技术等记录小尺寸重塑土样(土柱、土块或泥浆)失水开裂和湿化愈合过程，结合图像处理方法提取裂隙几何参数，研究土体裂隙发展演化规律，探讨裂隙的形成机理及影响因素。WELLS 等[17]认为现场土体受粗颗粒质量分数、结构及大气环境影响，小尺寸室内土体单元试验不能完全代表现场实际情况。据此，有学者开展了大气环境下原位土体裂隙监测试验[18-21]，在平面上采用图像处理技术提取裂隙几何参数，在剖面上开挖探槽测量裂隙深度，研究大气营力作用下土体裂隙发展演化规律。上述研究成果在一定程度上揭示了土体裂隙的发展演化规律，但单元试验中土样呈水平状态，且允许裂隙发育深度较小，难以反映存在临空面的裂土边坡在降雨-蒸发条件下坡体不同位置的裂隙在平面及深度方向的发展演化规律；现场试验虽然能反映大气营力对土体裂隙的影响，但由于外部环境及土层条件不可控，导致裂隙发展演化规律变异性较大。边坡模型试验能有效解决上述问题，同时可预先埋设传感器监测裂隙演化过程中土体内部物理参数，是研究裂隙发展演化规律的理想手段。目前，有关干湿循环作用下土质边坡模型试验逐渐增多。如王国利等[22-27]开展干湿循环作用下膨胀土边坡离心或缩尺模型试验，探究了膨胀土边坡破坏机理，试验研究成果对于揭示干湿循环条件下边坡变形破坏机理具有重要价值，但存在以下问题：1)未将裂隙作为关键因素考虑，没有系统研究模型边坡在干湿循环下裂隙平面及深度方向发展演化规律；2)研究仅局限于坡顶裂隙的平面发展演化特征；3)土体物理量(如基质吸力)对裂隙发展深度的影响不明；4)试验大多为小比尺模型试验，尺寸效应显著，且限制了裂隙在深度方向的充分发展；5)离心模型试验难以开展精确的人工模拟降雨，大多数研究采用人工喷壶洒水或直接浸水，无法模拟天然状态下雨水对边坡的打击、冲刷作用。为此，本文以现场裂土路堑边坡为原型，开展降雨-蒸发作用下足尺模型试验，测量土体表层质量含水率、基质吸力及裂隙深度，采用图像矢量化技术提取边坡不同位置土体裂隙几何参数，研究平面及深度方向裂隙发展演化规律，基于断裂力学分析裂隙类型，深化裂土边坡裂隙发展演化的认识。

1 试验设计

1.1 原型边坡

试验以安徽省沿江高速公路某灰白色裂土路堑边坡为原型，边坡高为3.2 m，坡率为1.0:1.0。边坡开挖暴露于大气环境一段时间后，坡面产生大量裂隙，如图1所示，降雨后雨水沿裂隙快速渗入边坡，导致坡体沿裂隙产生浅层破坏。

图1 现场原型边坡与坡面裂隙Fig.1 Field prototype slope and cracks in slope surface

1.2 足尺模型边坡填筑

依据原型边坡，设计模型边坡长×宽×高为6.0 m×3.0 m×2.8 m，坡率为1.0:1.0。试验所用土料取自原型边坡，土样基本物理性质如表1所示。模型边坡填土高2.8 cm，分14层填筑，每层厚20 cm，为尽可能与原型边坡土体物理力学性质保持一致，依据原型边坡天然密度(平均为1.81 g/cm3)计算每层所需填土质量，对土样翻晒、碾压打散、喷淋，按天然干密度为1.59 g/cm3，含水率为13.8%进行填筑。分层采用电动平板夯夯实，玻璃侧壁附近采用橡皮锤补夯，每层压实后采用环刀取样测试密度，若与设计值相差较大，则需翻松重新压实，同时利用温湿度探头(TDR-6A)快速检测土体体积含水率。筑坡完成后按设计坡率1.0:1.0 修坡，后静置72 h，图2所示为模型边坡。

表1 土样基本物理性质Table 1 Basic physical properties of soil samples

图2 模型边坡Fig.2 Model slope

1.3 降雨模式

模型试验的移动式降雨系统可控雨强范围为10.4～256.8 mm/h，降雨均匀系数能保持在80%以上，雨滴粒径为0.1～4.8 mm，雨滴终点速度可达2.0～2.9 m/s，降雨装置的设计及率定过程见文献[28]。

从2018-07-28T8:00—2018-08-8T19:18，试验共历时274.3 h，其中降雨10 次，降雨过程中雨强恒为15.2 mm/h。推开雨棚日晒7 次，平均日照强度为2.30～2.66 kW·h/m2，其余时间为无降雨无日晒阶段。将某次降雨经过日晒阶段后至下1次降雨开始前看作1 次降雨-蒸发过程。试验共经历5次降雨-蒸发过程。受天气影响，5次降雨-蒸发过程的降雨及日晒时间并不完全相等。降雨-日晒历程如图3所示。

1.4 观测方法及传感器布设

依托足尺模型边坡，选择坡体不同位置(坡脚、坡肩和坡顶)裂隙作为研究对象，通过定时拍照，测量裂隙深度、表层土体含水率和基质吸力等，研究模型边坡的裂隙发展演化规律。

1) 坡顶采用索尼IMX179 型USB 摄像头对指定裂隙区域按10 min 间隔进行定时拍照，摄像头经钢结构支架固定在坡顶面以上1 m；坡脚、坡肩部位采用索尼ICLE-6000L 型数码相机进行拍照，相机固定在坡脚前2 m，距地面1.5 m，为减小畸变对裂隙几何参数的影响，镜向与坡面垂直，并利用RM-VPRI 型定时器设置10 min 拍照间隔；通过图片坐标准确截取坡体不同部位面积S为3 721 cm2的裂隙观测区域，利用AutoCAD 将裂隙图像矢量化，(如图4 所示)，提取裂隙总长度L和总面积S0，按式(1)和式(2)分别计算裂隙率I和平均宽度d0。此外，图像处理过程中，对监测区域最后时刻(破坏前)的裂隙图像按5 cm间距进行划分，如图4(c)所示，在每个网格内裂隙与边界线交点的连线代表裂隙在该段的生长方向，统计裂隙生长角度的变化趋势。

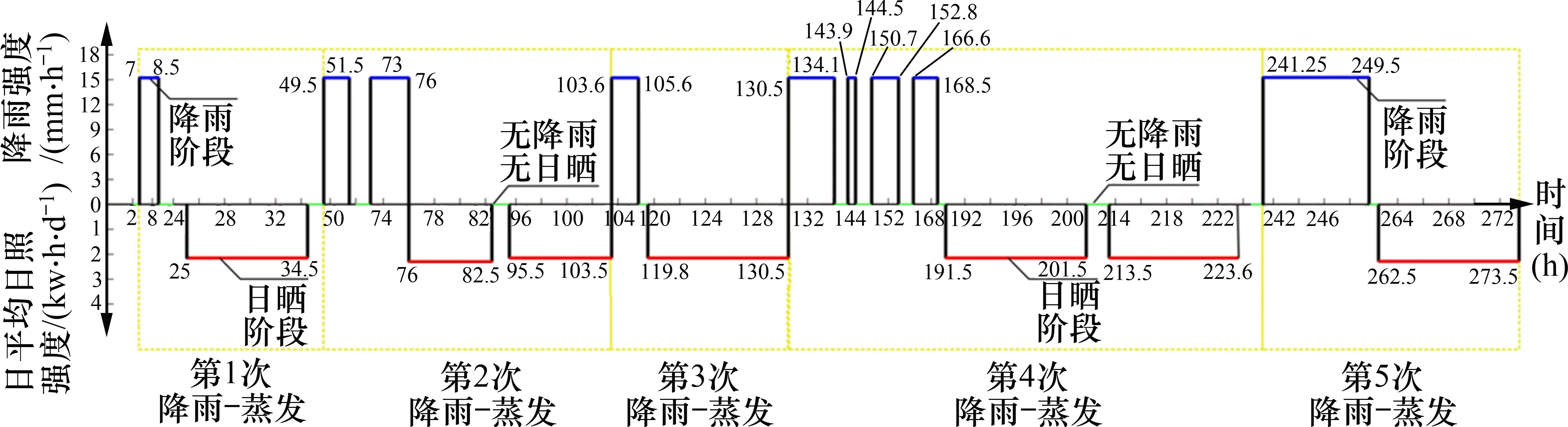
图3 降雨-蒸发历程图Fig.3 Time-history diagram of rainfall-evaporation cycles

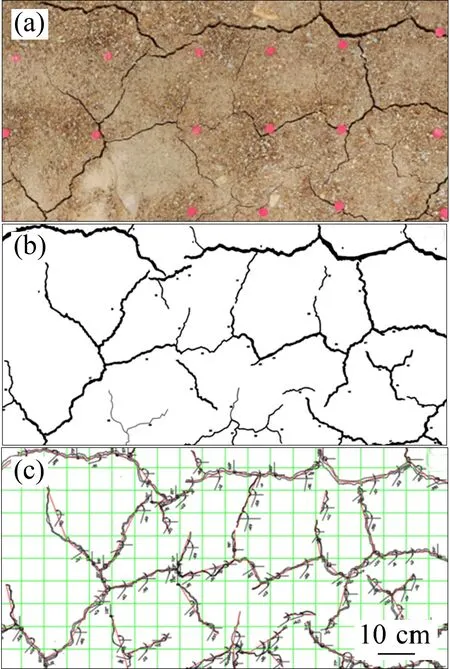
图4 坡顶裂隙图像、矢量图及生长角度测量Fig.4 Crack photo,vector picture and measurement of cracks growth angle at slope crest

2)每次降雨-蒸发阶段的降雨过程结束后，采用环刀在裂隙监测区域附近切取土样，将环刀置于不锈钢圆盒内，称取总初始质量后将其置于裂隙监测区域附近，放置前在圆盒底部用塑料薄膜与土体相隔，以避免底部沾染土体，试验过程中，每隔20 min称取1次总质量，前后质量差即为水分蒸发质量，用于换算蒸发量。

3)为跟踪监测裂隙发展演化过程中表层土体质量含水率变化规律，无降雨阶段在不同时刻钻取监测区域附近表层2～5 cm 深度土样，采用烘干法测量含水率；此外，选用2个MPS-2型土壤水势传感器(量程0～-500 kPa)分别埋设于坡顶裂隙监测区域表层以下10 cm 和20 cm 处，并在监测区域附近采用TEN 系列土壤水分张力计(量程0～100 kPa)监测30 cm 和40 cm 深度处土体的基质吸力。传感器布设位置如图5所示。

4)采用专用柔性软尺测量裂隙深度，单条裂隙深度取其长度方向上6个测点平均值，某一监测区域内裂隙深度取该区内主裂隙深度。

2 试验结果

试验共经历5 次降雨-蒸发过程，边坡不同位置裂隙率在试验过程中的变化曲线如图6所示，由图6可知：在整个试验过程中坡顶监测区域未发生破坏，具有完整的裂隙率曲线，坡脚、坡肩监测区域分别在第2 次和第4 次降雨-蒸发过程中发生破坏，裂隙监测结果终止于破坏前。

2.1 裂隙平面发展演化规律及影响因素

2.1.1 含水率与裂隙率

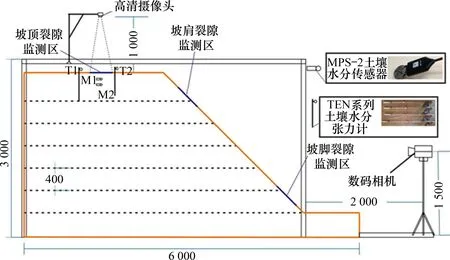
图5 图像采集设备及传感器布设示意图Fig.5 Layout of image acquisition device and sensor

图6 边坡不同部位的裂隙率变化曲线Fig.6 Variation curves of crack rate in different positions of the model slope

图7所示为不同部位表层土首次雨后干燥期间2018-07-28T16:00—2018-07-30T9:00含水率与裂隙率的变化曲线。由图7可知：坡脚、坡肩及坡顶的含水率变化趋势较一致，但坡脚含水率比坡肩和坡顶的大，这与坡脚密度大、蒸发率低及降雨期间径流积水有关；裂隙率曲线表明干燥过程中坡肩裂隙最发育，坡顶次之，坡脚最少，其中坡顶和坡脚变化趋势一致，坡顶与坡肩的含水率曲线较接近，但二者变化趋势明显不同。这是由于坡肩在雨后开裂过程中，不仅受蒸发收缩产生的张拉应力控制，而且还受下方土体单元容重增加后施加的拖曳力控制。因此，在降雨后4～18 h，在拖曳力与蒸发干缩共同作用下，坡肩裂隙率明显高于坡脚和坡顶裂隙率；随后进入日晒阶段，蒸发强度大幅增加，裂隙率陡增。日晒阶段结束后，坡肩裂隙发展重新回到受拖曳力控制的状态，由于下方土体单元容重减小，该阶段的斜率比最初受拖曳力控制时的斜率低，但仍大于仅受蒸发干缩作用控制的坡脚和坡顶裂隙的斜率。

图7 裂隙率与含水率时程变化曲线Fig.7 Time history curve of crack rate and water content

图8所示为裂隙率与含水率的变化规律。由图8可见：相同含水率条件下，坡肩裂隙率最大，其次为坡顶、坡脚；裂隙率与含水率呈负相关，坡脚、坡顶呈良好的线性关系，且坡顶裂隙率随含水率衰减速度快于坡脚；坡肩受下方土单元拖曳力影响，其整体裂隙率与含水率的线性拟合度较低，但当蒸发强度较大时，含水率与裂隙率仍具有良好的线性关系。

2.1.2 降雨蒸发次数与裂隙平面几何参数

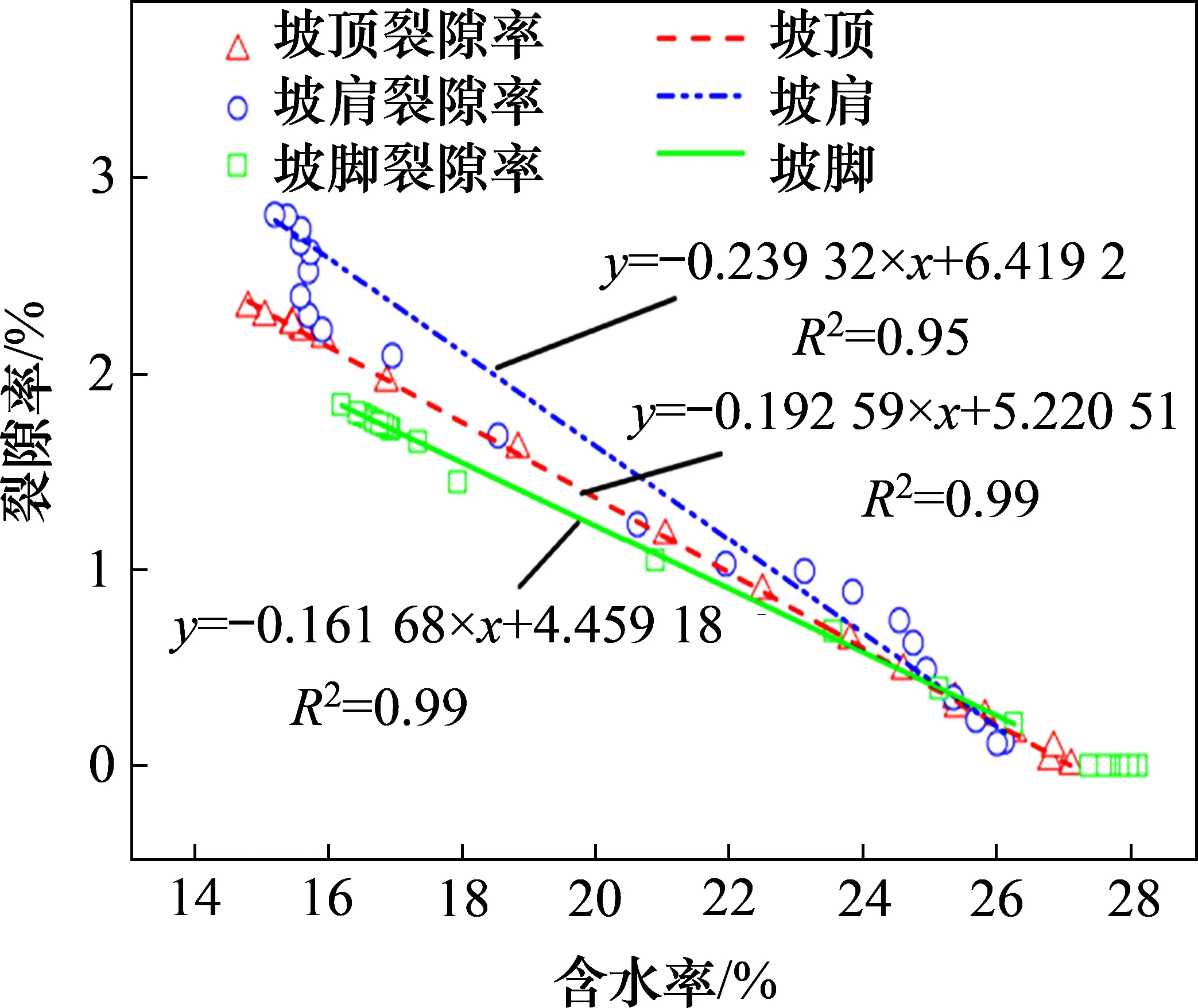
图8 裂隙率随含水率的变化规律Fig.8 Variation law of crack rate with water content

裂隙平面几何参数随降雨-蒸发次数的变化规律如图9 所示。由图9 可见：前3 次裂隙总长度与裂隙率变化趋势一致，起伏较大，裂隙平均宽度波动较小，在整个降雨-蒸发过程中基本呈增加趋势。后2 次降雨-蒸发阶段裂隙总长度趋于稳定，裂隙率随平均宽度增大而增加。上述结果表明在降雨-蒸发次数较少时，裂隙发育主要体现在裂隙长度上，随降雨-蒸发次数增加，切割土块的裂隙平面结构已基本成型，蒸发时水分主要从已发育的裂隙域中散失，被切割土块(土体基质域)结构致密，水分散失缓慢，难以产生新生裂隙，因此，该阶段裂隙发育主要表现在裂隙宽度上。前3次裂隙长度波动较大可能主要与平面裂隙结构未完全发育成型、受蒸降比(蒸发量/降雨量)影响较大有关。

在坡肩监测区域未发生滑塌之前，裂隙率坡肩最大，坡脚最小；裂隙总长度坡顶最大，坡肩次之；裂隙平均宽度坡肩最大，坡脚最小。试验结果表明：土体裂隙发育受含水率影响，而含水率受降雨-蒸发控制。

图10所示为降雨-蒸发过程中蒸降比变化直方图，图11所示为表层含水率随降雨-蒸发次数变化曲线。由图10和图11可知：坡脚在试验过程中蒸降比最小，含水率最高，因而裂隙发育程度低。坡肩部位裂隙受下方土体单元拖曳力影响，其宽度较仅受蒸发干缩作用的坡顶裂隙的宽度偏大。因此，即使坡肩蒸降比小于坡顶，含水率大于坡顶，其裂隙率及平均宽度变化曲线仍在坡顶之上。

2.1.3 裂隙平面几何演化特征

按图4(c)所示的方法对坡脚、坡肩及坡顶多处区域的裂隙最终发育状态进行处理，得到图12 所示的裂隙生长角度统计直方图。图12(b)中近平行走向(边坡走向，下同)表示生长角度为0°～45°及135°～180°裂隙，近垂直走向表示生长角度为45～135°裂隙。

由图12 可见：坡脚以发育近垂直走向裂隙为主，坡肩以发育近平行走向裂隙为主，坡顶2种方向裂隙发育程度基本均等而表现出网状形态。产生上述现象的原因主要是坡面裂隙在降雨-蒸发过程中会受到土单元拖曳力与推力的影响，处于坡面中部、坡肩及坡顶前缘位置的土体更容易发育与边坡走向平行的裂隙，而坡脚受上方土体单元推力难以发育平行边坡走向裂隙，土体储备的拉应力势能倾向于垂直于推力方向释放，因此，易发育与走向大角度相交的裂隙，坡顶中后缘受临空面影响较小裂隙呈网状发育，如图13所示。

2.2 裂隙深度发展演化规律及影响因素

2.2.1 基质吸力与裂隙深度

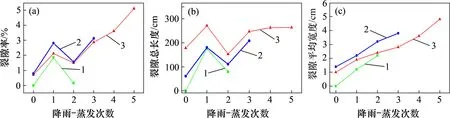
图9 裂隙平面几何参数随降雨-蒸发次数变化规律Fig.9 Variation law of plane geometric parameters of cracks with rainfall-evaporation cycles

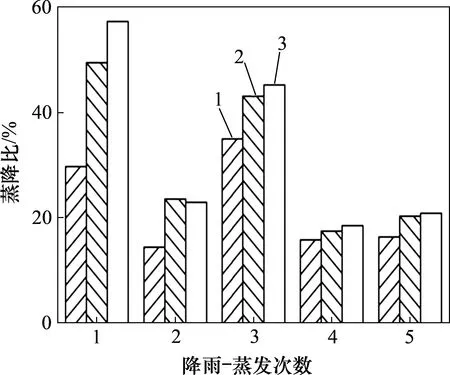
图10 降雨-蒸发过程中蒸降比变化直方图Fig.10 Histogram of evaporation/rainfall ratio versus rainfall-evaporation cycles

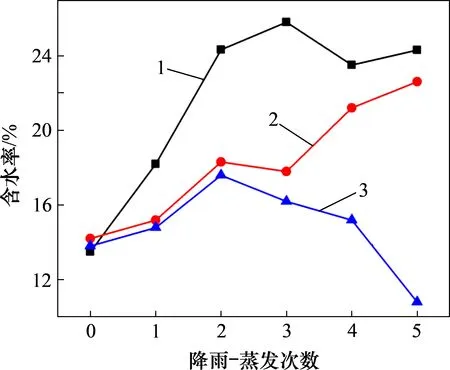
图11 表层含水率随降雨-蒸发次数变化曲线Fig.11 Variation curves of surface soil water content with rainfall-evaporation cycles

第4 次降雨-蒸发过程结束后，柔性尺可测得的裂隙平均深度为30.1 cm，经过第5次降雨-蒸发过程后深度发展至43.2 cm。图14所示为33.05 h内2018-07-28T10:15—2018-08-8T19:24不同深度基质吸力与裂隙深度的时程变化曲线。由图14可见：降雨开始前各测点处基质吸力由上至下分别为50.4，43.2，38.1 及20.3 kPa。降雨后，10，20 和30 cm 测点处基质吸力在1.5 h 内依次迅速降低至0，40 cm 测点由于裂隙尚未发展至此，其基质吸力在雨后4 h才降至0 kPa。降雨完成后，测区大量裂隙闭合，可测深度减小至0 cm；日晒蒸发过程前期，原裂隙迅速张开，陡增至降雨前深度，各测点处基质吸力增速较缓，在日照强度最大阶段2018-08-8T8:00—2018-08-8T16:30，10，20 和30 cm测点处因裂隙导致蒸发面增加，蒸发速率增大，基质吸力依次进入陡增阶段，40 cm测点处并未出现明显增长，该阶段裂隙向深处发展需要进一步撕裂完整土体，因此，其增长速率明显降低。日晒蒸发过程末期，40 cm测点处出现陡增，裂隙平均深度测量值表明此时裂隙已扩展至40 cm测点处附近，裂隙加速该区土体水分蒸发，由此引起测点处基质吸力快速增加。

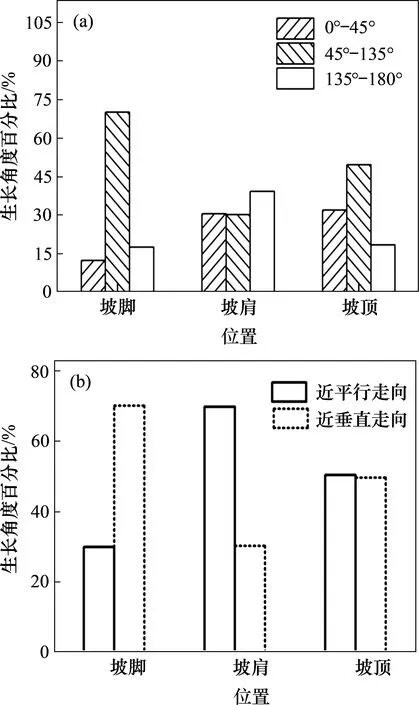
图12 裂隙生长角度统计直方图Fig.12 Statistical histogram of cracks growth angle

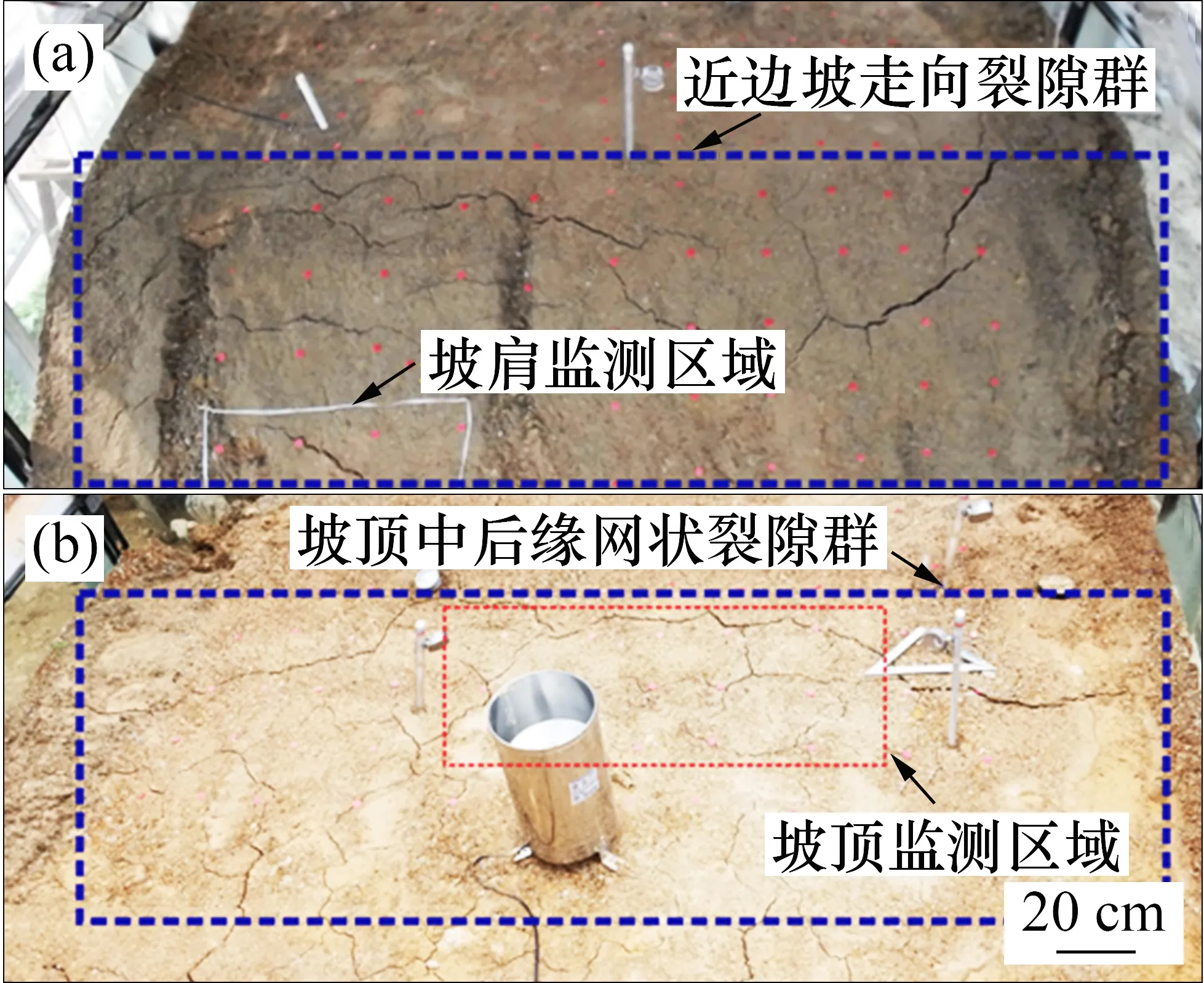
图13 坡肩及坡顶裂隙平面几何特征Fig.13 Plane geometry characteristic of cracks in slope shoulder and crest

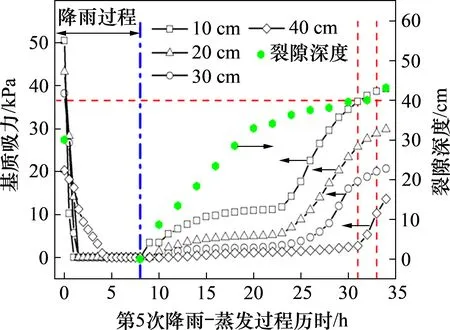
图14 基质吸力与裂隙深度时程变化曲线Fig.14 Curve of matrix suction and crack depth with time

2.2.2 降雨蒸发次数与裂隙深度

降雨-蒸发作用形成的裂隙在后一次降雨过程中，底部接受雨水下蚀作用深度增大，裂隙两侧土单元一方面遇水膨胀，另一方面在雨水冲刷作用下崩解堆积在裂隙内，形成松散堆积物导致裂隙闭合，如图15 所示。松散堆积物的抗拉强度远小于裂隙附近土块抗拉强度[11]，在蒸发过程中，原裂隙会迅速张开至降雨前深度，随后继续往纵深方向发展。

图16所示为主裂隙深度和宽度随降雨-蒸发次数的变化曲线。由图16可见：随降雨-蒸发次数增加，裂隙深度呈增加趋势，坡肩裂隙在发展过程中受下方土体单元拖曳力作用，其裂隙深度在第2～3 次降雨-蒸发过程中急剧增加。坡顶裂隙深度在前期无明显增长趋势。第2 次降雨-蒸发过程结束后，测量数据及模型箱侧壁显示裂隙深度进入加速发展阶段，如图17所示。此外，由图16还可知，主裂隙宽度与深度具有明显正相关性，这与文献[17]中结果相符。

2.2.3 裂隙竖向演化特征

图15 坡顶裂隙湿化愈合过程图Fig.15 Humidification healing process of cracks at slope crest

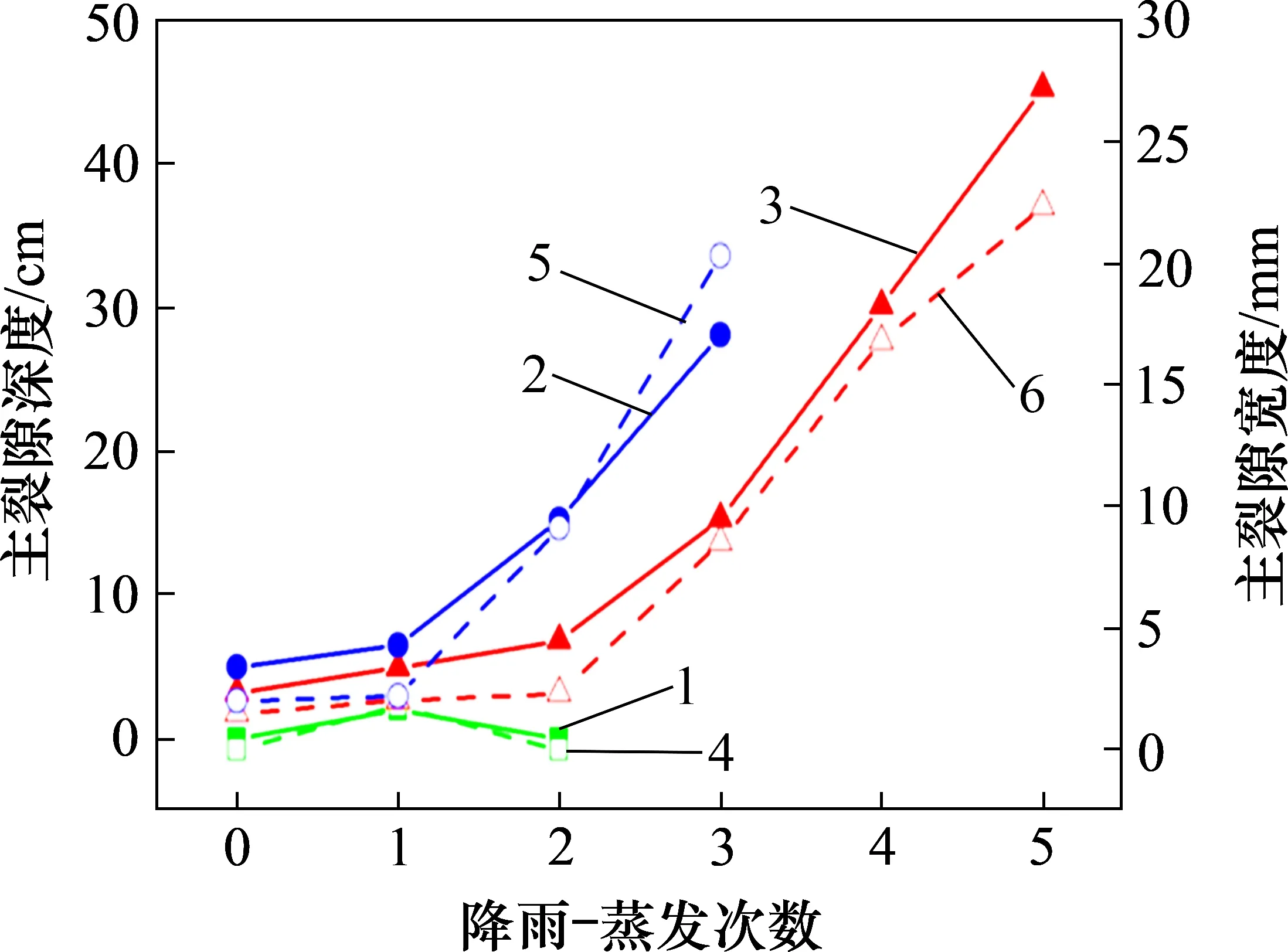
图16 主裂隙深度和宽度随降雨-蒸发次数的变化曲线Fig.16 Variation curves of depth and width of preferential crack with rainfall-evaporation cycles

图17 侧壁观察到的坡顶裂隙深度变化Fig.17 Depth variation of cracks on slope crest observed through glass side wall

当土体表层开裂时，土颗粒自重应力影响不明显；当裂隙向纵深方向发展时，自重应力影响增大。由土体蒸发干缩产生的张拉应力需要克服侧面上存在的2种抗拉应力，即土颗粒间的抗拉强度σa和土体自重引起的侧向应力σh，当裂隙尖端土体再次蒸发时收缩所产生的张拉应力大于σa+σh时，裂隙即可继续向深处发展。由于裂土具有低渗透性，上层土体蒸发收缩时下层土体并不紧跟其后，导致上下层土体不均匀收缩，加之裂隙越往深处发展，需要克服的抗拉应力越大，也越难开裂，因此，裂隙在纵剖面上往往呈“V”字型。水平土层中，当土体较为均匀时，裂隙往往竖直发育，竖向上不会有明显“转向”现象。对于坡面土体而言，侧向临空面导致σh减小，坡越缓，σh减小幅度越大，裂隙则越容易朝竖直方向发展。

图18 所示为坡体不同部位裂隙深度演化发展机理。由图18(a)可见：坡脚、坡面中部及坡肩在第1 次降雨-蒸发过程结束后均近竖直方向发育。由图18(b)可见：随降雨-蒸发作用，坡面裂隙发展不再只受土体干缩产生的张拉应力控制，裂隙两侧土体单元容重增大后，附加的拖曳力与推力开始控制裂隙向下生长，坡肩裂隙主要受下方土体单元的拖曳力，其裂隙逐渐向平行于坡面的方向发展，坡中裂隙同时受到上方土单元推力与下方土单元拖曳力作用，其裂隙尖端转向与坡面垂直的方向演化。坡脚处裂隙主要受上方土单元推力作用，在演化过程中裂缝深度及宽度越来越小，向下发展的方向也无明显变化。

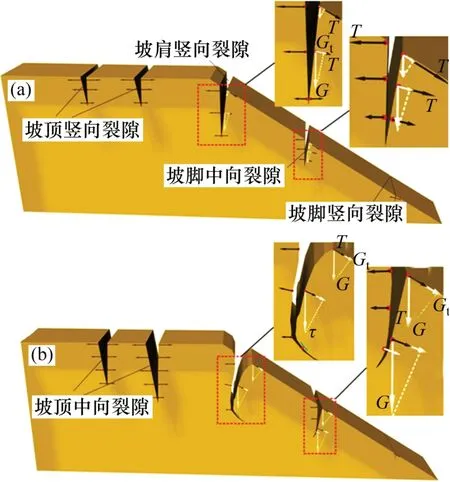
图18 坡体不同部位裂隙深度演化发展机理Fig.18 Evolution mechanism of crack depth in different positions of slope

3 裂土边坡裂隙类型划分

由试验分析结果可知：裂隙在平面及深度方向的演化特征与坡体位置密切相关，即裂隙的发展演化与土体所处的应力环境密切相关。断裂力学中，裂隙分为单型裂隙和复合型裂隙，单型裂隙可分为I 型张开断裂、Ⅱ型滑移断裂和Ⅲ型撕开断裂，如图19 所示。复合裂隙由上述3 种断裂复合而成。

图19 单一应力环境下3种断裂类型(引自文献[29])Fig.19 Three modes of cracks under single stress condition(cited from Ref.[29])

IRWIN[30]认为裂纹扩展与裂纹尖端附近应力场有关，并提出了I 型、Ⅱ型和Ⅲ型断裂的应力强度因子分别为KI，KⅡ和KⅢ。从应力角度看，当裂隙尖端附近应力强度因子满足下式时，裂隙则继续扩展：

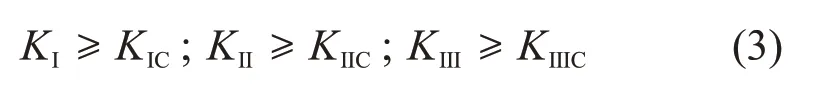
式中：KΙC，KⅡC和KⅢC分别为3种断裂的断裂韧度，表征土体抵抗开裂的能力。

能量角度上，能量释放率H是分析土体开裂的重要参数，指裂隙扩展单位面积时所释放的能量。在平面应变条件下，裂隙尖端能量释放率与断裂韧度有如下关系：

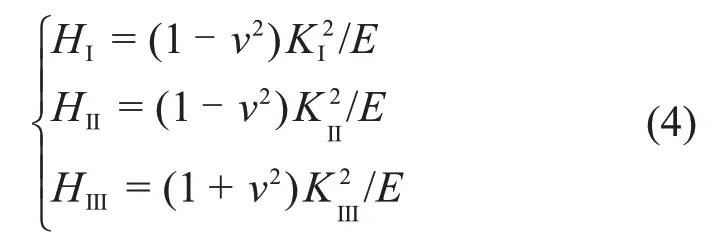
式中：HI，HⅡ和HⅢ分别为3 种断裂的能量释放率；E为弹性模量；v为泊松比。当裂隙尖端附近能量释放率满足下式时，裂隙则继续扩展：

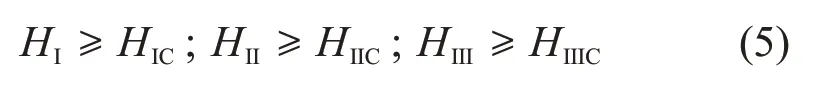
式中：HIC，HⅡC和HⅢC分别为3种土体开裂时的能量释放率临界值，与土体自身性质有关。对于复合型裂隙，H的表达式为

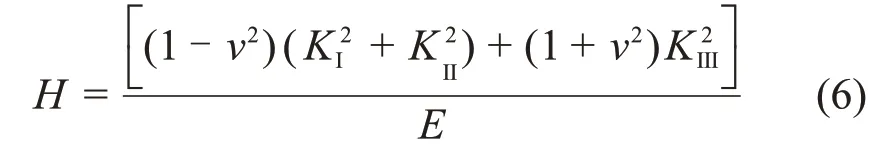
对应的断裂判据为

由蒸发干缩引起土体初次开裂并形成的裂隙均属I型张开断裂。张开断裂形成后在平面及深度方向即存在裂纹尖端，在降雨-蒸发过程中，随坡体不同位置应力状态变化，断裂类型及判据随之改变。

坡顶中后缘及坡脚张开断裂的进一步发展主要由水分蒸发产生的拉应力控制，其断裂类型仍属于I型张开断裂。当裂纹尖端有KΙ≥KΙC时，新的完整土体裂开，宏观上表现为裂隙深度及裂缝长度增加；裂隙初始开裂一般沿最大能量释放率Hmax方向，对于干缩裂隙指最大收缩能释放率。平面上，一条裂隙形成后，裂隙附近平行于裂隙长度方向有HI＜Hmax，垂直于裂隙方向存在HI≥Hmax，因此，新生裂隙往往垂直于已发育裂隙演化，同时，裂隙尖端向另一条已发育裂隙垂直生长，数次降雨-蒸发过程后，坡顶中后缘即形成网状结构裂隙。

如图18 所示，坡顶前缘、坡肩和坡面中上部张开断裂的进一步发展受T，τ和Gt控制，其断裂类型逐步演化为I-Ⅱ复合型断裂。在降雨期间及降雨后的一段时间内，复合断裂的H主要取决于Gt及HⅡ，其中HⅡmax方向平行于τ的方向，HImax方向垂直于T和Gt方向，因此，坡肩裂隙深度方向转向平行坡面发展，平面上近平行于边坡走向发展。

基于现场调研、模型试验和理论分析结果，提出如表2所示的裂土路堑边坡裂隙发展阶段及类型划分。