栅氧化层经时击穿的非平衡统计理论分析方法
2020-06-04赵文静丁梦光杨晓丽胡海云
赵文静 丁梦光 杨晓丽 胡海云
(北京理工大学物理学院, 北京 100081)(2020年1月15日收到; 2020年2月26日收到修改稿)
栅氧化层的经时击穿作为影响互补型金属-氧化物-半导体集成电路可靠性的一个重要因素, 一直是国内外学者研究的重点. 为了对其进一步研究, 首先从栅氧化层在电应力下经时击穿的微观机理出发, 基于栅氧化层中电子陷阱密度累积达到临界值时发生击穿的原理和电子陷阱生成过程的随机性, 提出了栅氧化层经时击穿的非平衡统计理论分析方法, 然后分别给出了恒定电流应力和恒定电压应力下电子陷阱生成速率方程, 导出了电子陷阱密度的概率密度分布函数. 最后以具体器件为例进行分析, 得到了栅氧化层的最概然寿命随电流应力、电压应力及其厚度的变化规律, 并类比固体断裂现象中“疲劳极限”的概念定义“击穿极限”概念. 计算出了累积失效率随电流应力、电压应力和时间的变化规律, 引入特征值来描述累积失效率达到0.63 所用的时间. 结果表明: 电子陷阱密度的概率密度分布函数满足对数正态分布, 且理论结果与实验结果相符.
1 引 言
金属-氧化物-半导体(metal oxide semiconductor, MOS)晶体管是微处理器、半导体存储器件等超大规模集成电路的核心器件, 随着大规模及超大规模集成电路的发展, MOS 晶体管的可靠性也成为人们研究的重点之一. MOS 晶体管中栅氧化层的完整性直接与集成电路的性能、可靠性以及成品率相关, 因此研究栅氧化层的可靠性非常有必要[1−3].
经时 击 穿(time-dependent dielectric breakdown, TDDB)是指施加的场强低于发生本征击穿时的场强, 在持续作用一段时间后发生的击穿. 人们常通过TDDB 来评估栅氧化层的本征可靠性,测试栅氧化层的质量[4]. 由于二氧化硅具有禁带宽度较大、介电强度较高、绝缘性好等优点, 一直是MOS 器件栅氧化层的主要材料. 本文以二氧化硅为例, 研究了电应力下栅氧化层的TDDB.
多年来, 人们为了了解栅氧化层的击穿机理,建立了许多模型, 其中包括电子俘获击穿模型[5]、空穴击穿模型[6]、感生共振隧穿模型[7]、陷阱产生相关模型[8]等. 而针对击穿过程的随机性, 也有一些模型, 如马仲发等[9]提出的逾渗模型, 其认为栅氧化层中深能级缺陷产生与积累, 形成电导逾渗通路, 造成击穿. Lee 等[10]的统计模拟模型把栅氧化层中缺陷的存在看作其减薄, 并认为栅氧化物层的寿命与空穴通量达到某一特征值所需的时间有关.Suñé等[11]将MOS 电容器分成若干个柱状“小元胞”, 并将其定义为“击穿前退化点的区域”, 用泊松分布描述一个元胞中电子陷阱出现的概率, 假设当其中产生一定数量的电子陷阱时, 该元胞发生击穿. 但到目前为止, 栅氧化层经时击穿的物理机理依然没有完全定论, 一般认为其与栅氧化层中产生的电子陷阱有关. 本文以动态平衡模型[12]为基础,提出了栅氧化层经时击穿的非平衡统计理论分析方法, 为计算MOS 器件中栅氧化层的累计失效率、定量的分析其退化程度提供了一个新方法.
2 栅氧化层经时击穿的微观机理
在电应力作用下, 栅氧化层的TDDB 过程通常可分为两个阶段: 损伤建立阶段和突变失控阶段. 在损伤建立阶段, 因电子与二氧化硅晶格发生碰撞, 注入电子的部分动能被耗散, 被耗散的动能可能造成二氧化硅中Si-O 键的断裂, 而产生电子陷阱. 当局部电子陷阱密度达到临界值Nbd时, 在电极之间产生欧姆通道, 进入突变失控阶段, 其中电或热的正反馈作用导致击穿. 二氧化硅单位体积中Si-O 键的数量是一定的, 即可以产生的陷阱数量是一定的, 所以临界陷阱密度Nbd与测试所用应力条件无关, 与制作工艺、面积、厚度有关[13−15].由于突变失控阶段经历时间较短, 所以一般将损伤建立阶段的时间就看作栅氧化层的寿命[6,16]. 本文只研究损伤建立阶段.
随着MOS 器件尺寸的缩小, 栅氧化层逐渐变薄, 而工作电压却不能随之减小, 所以此时的隧穿电流主要是Flower-Nordheim 隧穿电流. 人们一般采用恒定电流应力和恒定电压应力方法[17]研究栅氧化层的TDDB 特性.
设恒流应力下t时刻二氧化硅中产生的电子陷阱密度为Nj(t) , 恒压应力下t时刻二氧化硅中产生 的电子陷阱密度为Nu(t) . 它们可分别表示为[14]

其中N0为初始陷阱密度,e为元电荷量,l为栅氧化层厚度,ε为栅氧化层的介电常量,U0为恒流应力下的初始电压,τu为电压的驰豫特征时间, 与新电子陷阱的产生有关,K2为与电子的有效质量和势垒高度有关的常量,E0为外加电场强度,τj为测试中电流密度的驰豫特征时间, 且
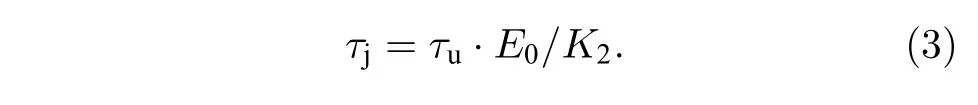
3 非平衡统计理论分析方法
由于材料结构本身等的不均匀性, 在电应力作用下, 栅氧化层中产生电子陷阱的位置和速率具有随机性. 随着时间的增加, 在电应力作用下, 栅氧化层中产生的电子陷阱数不断增多, 对栅氧化层造成损伤. 当两个电子陷阱接触时, 就可合并成一个较大的电子陷阱. 如果产生的电子陷阱形成了连接两个电极的欧姆通道, 就会造成栅氧化层击穿, 此击穿过程是不可逆的. 由于电子陷阱的生成过程的随机性和不可逆性, 故电子陷阱的生成速率可用广义的Langevin 方程来描述[18,19]:

假设电子陷阱的生成速率与达到的退化程度无关, 只与当时及稍早施加的电应力和栅氧化层的微观结构有关[11], 故可将电子陷阱的生成过程看作一个马尔可夫过程, 涨落函数f(t) 服从如下高斯分布:

其中D为涨落长大系数,d为Dirac 函数.
根据随机理论[20], 与Langevin 方程(4)等价的Fokker-Plank 方程, 即电子陷阱密度的概率密度分布函数P(N0,N,t) 随时间的演化方程为

其中P(N0,N,t)dN表示在电应力下, 栅氧化层中的电子陷阱密度由初始 (t=0 s)时的N0 在t时刻增长到N~N+dN之间的概率. 根据局部电应力涨落和结构背景涨落的特点,k(N),β(N) 和D的关 系为[18]

其中A为一个与电子陷阱密度N无关的常量,h为总的相对偏差,tbd为栅氧化层的最概然寿命.将(7)和(8)式代入(6)式, 采用路径积分法可得电 子陷阱密度的概率密度分布函数P(N0,N,t) 为[18]

4 恒流应力下的经时击穿研究
对(1)式求导可得, 恒流应力下栅氧化层中电子陷阱的平均生成速率k(Nj) 为

对比(10)与(7)式可得

将(11)式代入(9)式可得, 电子陷阱密度的概率密度分布函数P(N0,Nj,t) 为
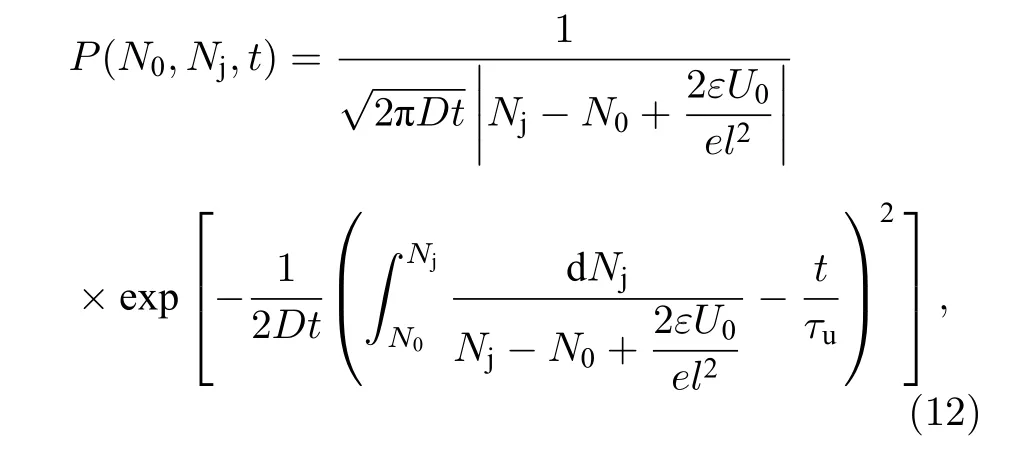
从(12)式可以看出, 当指数项为1时, 电子陷阱概率密度函数值最大, 即此时为电子陷阱密度的最概然值. 所以恒流应力下栅氧化层中电子陷阱密度从初始值N0累计到Nbd的最概然时间, 即最概然寿命为

根据(13)式, 并结合他人[21,22]实验中MOS 器件两种样品的数据进行分析, 得到栅氧化层的最概然寿命tbdj随其厚度l和初始电压U0的变化规律如图1 所示. 其中, 样品1[21]和样品2[22]的厚度分别为l1= 10 nm,l2= 11 nm; 初始电子陷阱密度为N0=1.5×1016cm−3[23]; 临界电子陷阱密度分别为Nbd1=4.3×1018cm−3,Nbd2=6.5×1018cm−3; 初始电压分别为U01=13V ,U02=12V .
从图1 可以看出, 恒流应力下, 如果不考虑临界电子陷阱密度Nbd随栅氧化层厚度l的变化, 则栅氧化层的最概然寿命tbdj随其厚度l的增大而增大, 随其初始电压U0的增大而减小. 这可能是由于栅氧化层厚度l的减薄和初始电压U0的增大会导致其上电场强度增大, 使其更容易被击穿, 造成其寿命tbdj减小.

图1 不同厚度栅氧化层的最概然寿命(a)样品1[21],J =1 A/cm2 ; (b) 样品2[22], J =0.8 A/cm2Fig. 1. The most probable lifetime of gate oxide with different thickness: (a) Sample 1[21] at J =1 A/cm2 ; (b) sample 2[22] at J =0.8 A/cm2 .
当栅氧化层的材料、厚度、制作工艺、所处温度一定时, 电压的驰豫特征时间τu和电流密度J的乘 积为一个常量, 即[14]

由(13)和(14)式可得栅氧化层的最概然寿命tbdj与电流密度J的关系曲线, 并与实验结果进行对比, 如图2 所示. 类比固体断裂现象中“疲劳极限”的概念定义“击穿极限”, 其表示当电流应力低于某一值时, 很难发生TDDB. 由图2 可以看出, 样品1的“击穿极限”大约在 0.05 A/cm2, 样品2 的“击穿极限”大约在 0.1 A/cm2, 在此电流应力下, MOS器件基本可以安全使用; 理论结果与实验结果[21,22]趋势一致, 即栅氧化层的最概然寿命tbdj随所加电流密度J的增大而减小. 但理论上推出二者是非线性关系, 与实验定量上有差别, 这或许是由于所能获得的实验数据较少, 或许是源于理论在微观机理上考虑的因素不够全面.

图2 不同电流密度对应的栅氧化层的最概然寿命 (a) 样品1; (b) 样品2Fig. 2. The most probable lifetime of gate oxide under different electric current density: (a) Sample 1; (b) sample 2.
根据(12)式可得, 在电流密度J不变(即电压的驰豫特征时间τu不变)的情况下, 不同时刻电子陷阱密度的概率密度分布如图3 所示. 显而易见,电子陷阱密度的概率密度分布函数服从对数正态分布. 概率密度函数曲线的峰值代表某一时刻电子陷阱密度Nj(t) 的最概然值. 样品1 在电流密度J=1 A/cm2(样品2 在电流密度J=0.8 A/cm2)的情况下, 不同时刻, 栅氧化层中电子陷阱密度Nj(t)的最概然值不同; 随着恒流应力作用时间的增加, 概率密度函数曲线的峰值向右移, 说明电子陷阱密度Nj(t) 随时间t的增加而增加; 峰高越来越小, 半峰宽越来越大, 说明随时间的增加电子陷阱数量增加, 电子陷阱密度的概率密度分布趋向于均匀化.

图3 不同时刻的P-N 图 (a) 样品1, J =1 A/cm2 ; (b)样品2, J =0.8 A/cm2Fig. 3. The probability density varies with electron trap density at different time: (a) Sample 1 at J =1 A/cm2 ;(b) sample 2 at J =0.8 A/cm2 .
在时间t不变的情况下, 不同电流密度J下电子陷阱密度的概率密度分布如图4 所示. 从图4 中可以看出, 在时间t=20 s时, 随着电流密度J的增大, 概率密度函数曲线的峰值向右移动, 说明电子陷阱密度Nj(t) 随着电流密度J的增大而增加.因为当电流密度增大时, 相应的就需要更大的栅极电压, 在栅氧化层厚度不变的情况下, 电压越大,其中的电场强度越大. 注入的电子被加速到更大的速度, 因而获得了更大的能量. 使得电子与二氧化硅中的晶格碰撞时被散射的那部分能量也成比例增加. 因此产生的电子陷阱数也随之增加. 所以在同一时刻, 被施加电流应力大的二氧化硅中产生的电子陷阱数量更多. 随着电流的增大, 概率密度函数曲线的峰高越来越小, 半峰宽越来越大. 说明随着电流的增大, 概率密度分布趋向于均匀化.

图4 不同电流密度下的P-N 图( t =20 s ) (a) 样品1;(b) 样品2Fig. 4. The probability density varies with electron trap density under different electric current density( t =20 s ):(a) Sample 1; (b) sample 2.
将某一电应力下, 概率密度分布函数P(N0,Nj,t) 从临界电子陷阱密度Nbdj积分到无穷大 , 即可得到MOS 器件的累积失效率F为

结合(15)和(12)式, 并代入数据计算可得某一恒流应力下的累积失效率.
图5 和图6 分别是样品1 和样品2 在不同恒流应力下, 累积失效率F随时间t的变化曲线.
其中,C0为t=0时刻欧式看涨期权价格;S0为t=0时刻基础资产(股票)价格;X为敲定价格;r为无风险利率;q为股息收益率;τ为期权到期时间;Πj(j=1,2)的定义如下[14]:
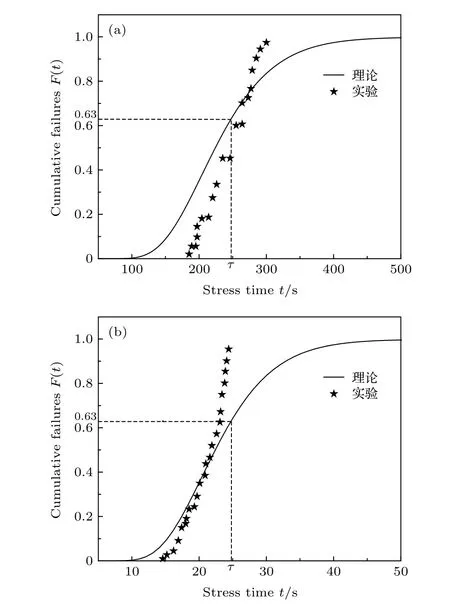
图5 样品1 中两种不同电流密度的累积失效率 (a) J =0.1 A/ cm2; (b) J =1 A/cm2Fig. 5. Breakdown cumulative distributions for two different electric current densities in sample 1: (a) J =0.1 A/cm2 ; (b) J =1 A/cm2 .

图6 样品2 中三种不同电流密度的累积失效率 (注: 实心五角星代表实验值, 线段代表理论值.)Fig. 6. Breakdown cumulative distributions for three electric current densities in sample 2. (Note: solid five-pointed star represents experimental value and line segment represents theoretical value.).
当累积失效率F达到0.63时, 大部分器件发生击穿失效, 且此时测试参数不受前期失效的影响, 与累计失效率为1时的测试参数接近[17], 所以取累积失效率F达到0.63 所用的时间τ作为特征值, 即

τ可看做击穿过程的“时间尺度”,τ越大则累积失效率F达到0.63 所需时间越长, 栅氧化层的寿命越长.
从图5和图6中可以看出, 当样品1 在电流密度J为0.1 A/cm2和1.0 A/cm2时,τ分别为249.8 s 和24.9 s; 样品2 在电流密度J为 0.4 A/cm2,0.6 A/cm2和0.8 A/cm2时,τ分别为58.7 s, 39.4 s和 28.1 s. 累积失效率F随时间t的增大逐渐增大,在短时间内达到1, 且电流密度J越大, 累积失效率F达到1 所用的时间越短, 这个结果与实验结果[21,22]一致.
5 恒压应力下的经时击穿研究
同理可得, 在恒压应力下, 电子陷阱的平均生产速率k(Nu) 为
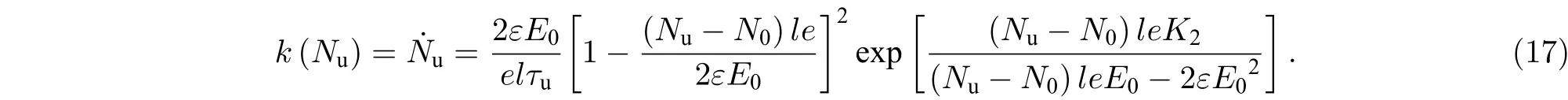
对比(17)与(7)式可得

电子陷阱密度的概率密度分布函数P(N0,Nu,t) 为

在恒压应力下, 栅氧化层中陷阱密度Nu(t) 达到临界值Nbd的最概然时间, 即最概然寿命tbdu为

由(20)式可知, 不考虑临界电子陷阱密度Nbd随栅氧化层厚度l的变化, 最概然寿命tbdu随样品厚度l的增大而增大, 随电场强度E0的增大而减小.
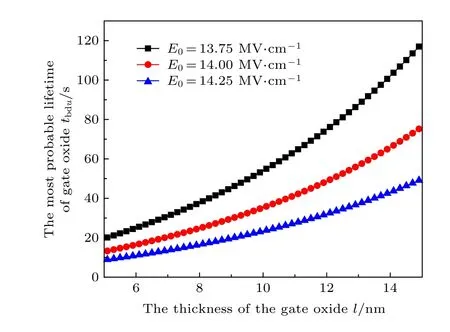
图7 不同厚度的栅氧化层的最概然寿命Fig. 7. The most probable lifetime of gate oxide with different thickness.

图8 不同电场强度对应的栅氧化层的最概然寿命Fig. 8. The most probable lifetime of gate oxide under different electric field.
根据样品2 的数据进行分析, 不同厚度的栅氧化层的最概然寿命tbdu如图7 所示;不同恒定电场E0下, 栅氧化层的最概然寿命tbdu如图8 所示. 从图8 中可以看出, 栅氧化层的寿命tbdu随电场强度E0的增大而减小, 其“击穿极限”大约为 5 MV/cm ,且与实验结果[22]趋势一致.
根据(19)式得到相同电场下, 不同时刻栅氧化层中电子陷阱密度的概率密度曲线如图9 所示;以及同一时刻, 不同电场下的概率密度曲线如图10所示. 由图9 和图10 可以看出, 随电场强度E0和时间t的增大, 电子陷阱密度的概率密度的最概然值逐渐增大, 且电子陷阱密度的概率密度分布趋于均匀.

图9 E 0 =13.75 MV·cm−1时, 不同时刻的P-N 图Fig. 9. The probability density varies with electron trap density at different time under E 0 =13.75 MV·cm−1 .
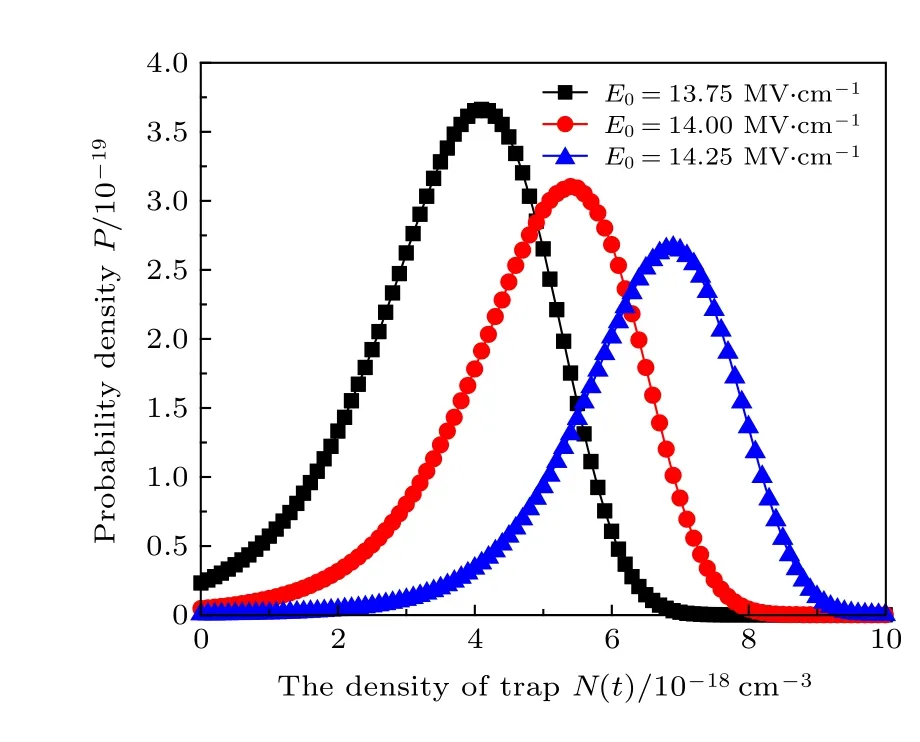
图10 t =30 s时, 不同电场强度下的P-N 图Fig. 10. The probability density varies with electron trap density at t =30 s under the different electric field.
根据(15)式可得某一恒定电场强度E0下的累积失效率F随时间t变化的图像, 并与实验结果[22]进行了对比, 如图11 所示. 当K2= 100 MV/cm时, 理论结果与实验结果拟合较好, 但实验得到K2的值一般在200 MV/cm 左右[24]. 可以看出, 当电场强度E0为13.7 MV/cm, 14.00 MV/cm和14.25 MV/cm时,τ分别为71.8 s, 46.8 s 和30.7 s, 即随电场强度E0增大栅氧化层的寿命变短; 随时间t和电场强度E0的增大, 累积失效率F逐渐增大, 且理论结果与实验结果相符.
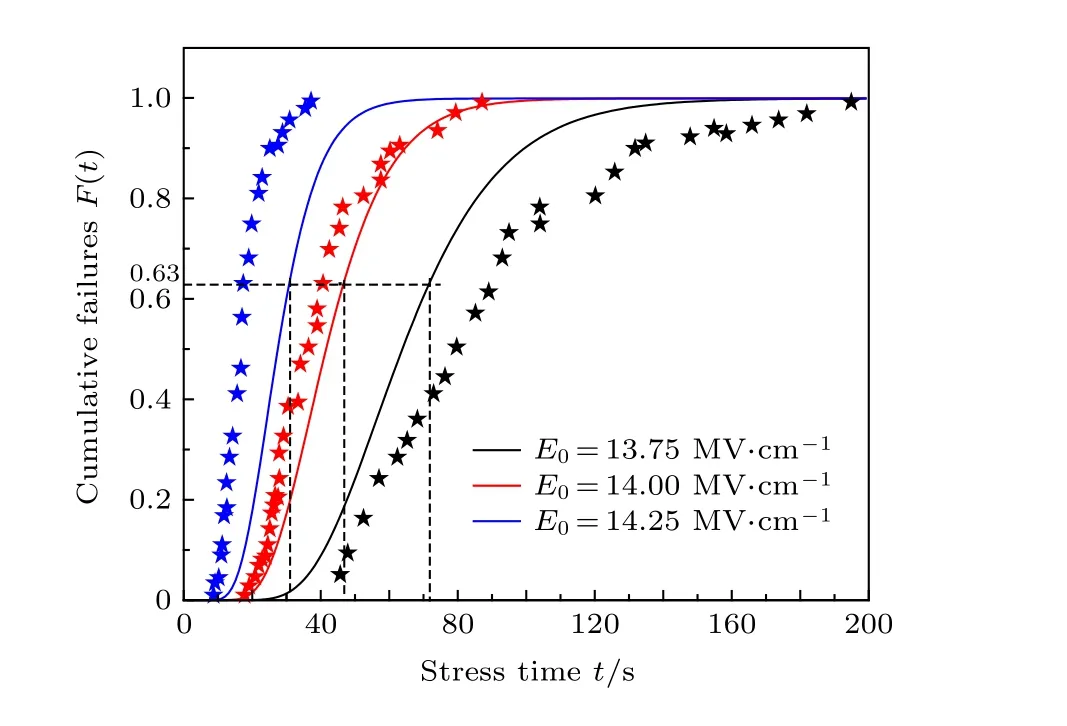
图11 三种不同电压下的累积失效率Fig. 11. Breakdown cumulative distributions for three different electric field.
6 结 论
本文基于栅氧化层中电子陷阱生成过程的随机性, 在动态平衡模型的基础上提出了栅氧化层经时击穿的非平衡统计理论分析方法, 并以具体的MOS 器件为例, 分别研究了在恒流应力、恒压应力情况下栅氧化层的寿命、电子陷阱密度的概率密度分布函数、累积失效率. 所得结论如下:
1) 分别对不同电应力下、不同厚度的栅氧化层进行了寿命预测; 得到在相同电流应力、电压应力下, 栅氧化层中电子陷阱密度的概率密度分布函数随时间的变化曲线; 同一时刻下, 栅氧化层中电子陷阱密度的概率密度分布函数随所加电流、电压的变化曲线, 以及累积失效率随时间、电流应力、电压应力的变化曲线.
2) 类比“疲劳极限”概念提出了“击穿极限”概念, 引入特征值作为击穿过程的时间尺度, 描述累积失效率达到 0.63 的时间.
3) 发现栅氧化层中电子陷阱密度的概率密度分布函数服从对数正态分布, 得到的累积失效率虽与Weibull 分布所得的累积失效率形状相似, 但Weibull 分布是基于简单的统计假设, 而非平衡理论方法是从微观机理出发严格导出的.
随着MOS 器件的变小, 栅氧化层逐渐减薄,其在电应力下TDDB 的微观机理发生了变化, 动态平衡模型可能不再适用, 但我们依然可以使用非平衡统计理论方法来描述其退化程度、计算累计失效率、预测其寿命.
