变换——让抛物线演绎新的精彩

文 崔恒刘

平移、旋转和翻折是几何变换中的三种基本变换，近年来，它们携手抛物线，共同演绎了新的精彩。

一、平移

例1（2019·山东淄博）将二次函数y=x2-4x+a的图像向左平移1个单位，再向上平移1个单位。若得到的函数图像与直线y=2有两个交点，则a的取值范围是（ ）。

A.a＞3 B.a＜3 C.a＞5 D.a＜5

【解析】我们应先利用配方法将y=x2-4x+a化为顶点式，即y=x2-4x+a=（x-2）2-4+a，得顶点坐标为（2，-4+a）。图像向左平移1个单位，再向上平移1个单位，则其顶点为（1，-3+a），因此得到的函数解析式为y=（x-1）2-3+a=x2-2x+a-2。再将y=2代入，得 2=x2-2x+a-2，即x2-2x+a-4=0。由题意“函数图像与直线y=2有两个交点”，所以Δ=4-4（a-4）＞0，解得a＜5。故选D。

【点评】几何图形平移变换后，改变的只是位置，而形状、大小都没有变。对于二次函数抛物线而言，平移不改变抛物线的开口方向、大小（二次项系数不变）。同学们解题时要抓住抛物线平移的关键——顶点，由顶点的平移判断整个抛物线的平移，据此求出函数解析式。

二、翻折

例2（2019·四川资阳）图1是函数y=x2-2x-3（0≤x≤4）的图像，直线l∥x轴且过点（0，m），将该函数在直线l上方的图像沿直线l向下翻折，在直线l下方的图像保持不变，得到一个新图像。若新图像对应的函数的最大值与最小值之差不大于5，则m的取值范围是（ ）。

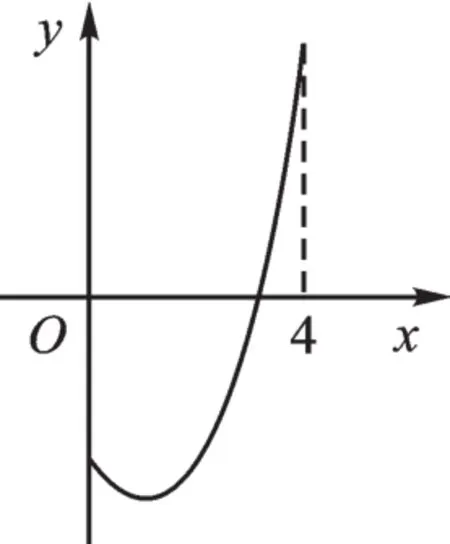
图1

A.m≥1 B.m≤0

C.0≤m≤1 D.m≥1或m≤0

【解析】已知图像是二次函数y=x2-2x-3上的一部分。我们先求出图像上的关键点：由y=（x-1）2-4，得其顶点坐标为（1，-4）。当x=0时，y=-3，所以A（0，-3）；当x=4时，y=5，所以C（4，5）。

直线l与x轴平行，移动直线l，观察：当m=0时，如图2所示，D（4，-5），此时最大值为0，最小值为-5；当m=1时，如图3所示，此时最小值为-4，最大值为1；当1＜m＜5时，最大值与最小值之差大于5，不合题意。综上所述：0≤m≤1，故选C。

图2

图3

【点评】此题将几何变换的翻折引入二次函数的问题中，解题时我们应结合函数图像，借助几何直观，不断尝试操作，改变动直线的位置，找出最大值和最小值的差刚好为5的m的临界值。

三、旋转

例3（2019·辽宁大连）把函数C1：y=ax2-2ax-3a（a≠0）的图像绕点P（m，0）旋转180°，得到新函数C2的图像，我们称C2是C1关于点P的相关函数。C2的图像的对称轴与x轴交点坐标为（t，0）。

（1）填空：t的值为________；（用含m的代数式表示。）

（2）若a=-1，当时，函数C1的最大值为y1，最小值为y2，且y1-y2=1，求C2的解析式；

（3）当m=0时，C2的图像与x轴相交于A、B两点（点A在点B的右侧），与y轴相交于点D。把线段AD绕原点O逆时针旋转90°，得到它的对应线段A′D′，若线段A′D′与C2的图像有公共点，结合函数图像，求a的取值范围。

【解析】（1）C1：y=ax2-2ax-3a=a（x-1）2-4a，顶点（1，-4a）绕点P（m，0）旋转180°的对称点为（2m-1，4a），C2：y=-a（x-2m+1）2+4a，函数的对称轴为x=2m-1，所以t=2m-1，故填2m-1。

（2）当a=-1时，C1：y=-（x-1）2+4。

①当时，则时，有最小值时，有最大值y1=-（t-1）2+4，则，无解。

②当时，则x=1时，有最大值y1=时，有最小值（舍去）。

③当时，则x=1时，有最大值y1=4；x=t时，有最小值y2=-（t-1）2+4，则y1-y2=（t-1）2=1，解得t1=0（舍去），t2=2。

故C2：y=（x-2）2-4=x2-4x。

（3）m=0，C2：y=-a（x+1）2+4a。

则各点坐标分别是A（1，0）、B（-3，0）、D（0，3a）、A′（0，1）、D′（-3a，0）。

当a＞0时，a越大，则OD越大，点D′越靠左。

当C2过点A′时，y=-a（0+1）2+4a=1，解得当C2过点D′时，同理可得a=1，故或a≥1。

当a＜0时，当C2过点D′时，-3a=1，解得，故。

【点评】本题考查二次函数的性质及旋转的性质，涉及中心对称，图形全等，一次函数、二次函数的性质等，综合性强，解题的关键是求出二次函数图像的顶点坐标。