初中平面几何折叠问题解题策略

徐飞雷

摘 要：本文聚焦初中数学平面几何的折叠问题，根据折叠过程中的基本性质，总结了三种解题技巧，学生的直观想象能力和逻辑推理能力等数学核心素养。

关键词：折叠问题;轴对称;解题策略

中图分类号：G633.63文献标识码：A     文章编号：1992-7711（2020）07-072-2

“折叠”作为图形的三大运动之一，题型多样，变换灵活，多以折叠问题为主要载体综合其他几何图形的知识进行考察。因“图形复杂”、“关系复杂”而成为中难题，学生在紧张的考试过程中解有关“折叠”的问题，一旦不能做到胸有成竹，便会产生浮躁的情绪，只有了解了折叠问题的本质，才能迅速找到破解折叠问题的方法。

“折叠”的本质是“轴对称”，因此，画一个图形折叠后的图形，是采用画轴对称图形的方法：先画出各个点的对称点，再连结对应的线段。一般情况下，画图的方法，就揭示了图形的性质，折叠前后的两个图像是全等的;折痕所在直线为全等图形的对称轴;对称点的连线被对称轴垂直平分等，合理运用这些性质就能找到解题的方法。

本人结合教学实际，总结了“折叠”问题的三种解题策略。

策略一、利用“折叠前后的两个图形全等”的性质

这是初中数学中“折叠问题”使用的最多的一种解题思路，利用折叠前后的图形相互重合，是全等形，得到对应的线段、角、面积、周长等都相等，那么，如何在这么多相等的量中找到有用的等量关系呢？一般情况下，条件和结论中描述到的量会用到它的等量，图形中已经能够确定的量会用到它的等量，这些量之间的关系较为复杂，因此在思考问题时一定要学会标注图形，这样可以帮助我们理清边角的关系，快速找到解题思路。

此题折叠过程较为简单，沿AD进行折叠，可以直观的看出折叠前后的两个全等三角形，再根据其他条件，进行简单推理证明，即可得到线段间的等量关系。

策略二、利用“对称点的连线被对称轴垂直平分”的性质

这也是初中数学中“折叠问题”常用的一种解题思路，因此在解决有关折叠问题时，如果策略一不能解决问题，往往要考虑连接对称点，利用“对称点的连线被对称轴垂直平分”这一定理来解决问题，特别的，当题目中涉及到“对称点的连线”或“折痕线段”时，一般要优先考虑用此法。

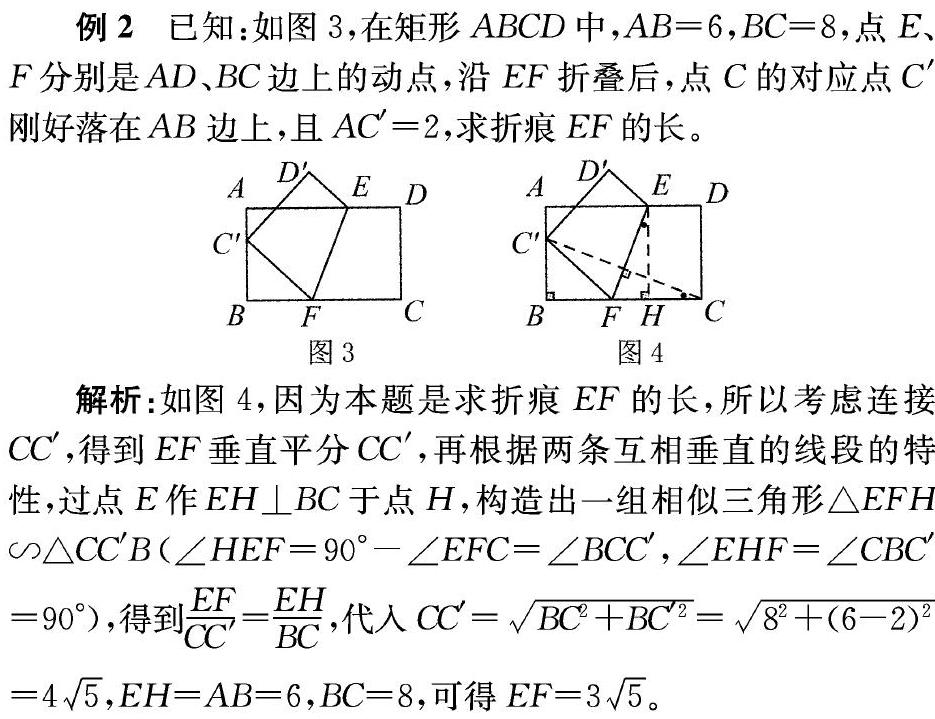
解决折叠问题，不仅需要了解折叠的过程，还需要把握折叠的基本性质，即“全等”和“垂直”。这道题需要添加辅助线才能构造出图4，以折叠为载体，考察了折叠的性质，勾股定理、相似的判定与性质，把要求的线段放到三角形中，利用相似来求解。

策略三、利用“反折叠图形”的思路

最近几年有关折叠问题的新题中，经常会看到“相对运动”的思想，即“反折叠”，它是指把一个图形按与原折叠方向相反的方向折叠。如：原图形画出了折痕右边的部分折叠到左边后的图形，“反折叠”图形就是画出折痕左邊的部分折叠到右边后的图形。

“折叠”的本质是“轴对称”，折痕是一条穿过图形的对称轴，沿着折痕把一个图形“从左往右折”和“从右往左折”得出的图形是完全相同的。原题给出的折叠图形往往只有一半图形的对称图形，另一半图形的对称图形不会画出来，这就为解题设置了障碍，使关键点无法找到对称点，化解之法就是再画出另一半图形的对称图形，这样，就得到了整个图形关于折痕的完整对称图形。一般情况下，出现“折叠后某直线满足某某条件”（如：折叠后“某某线经过某点”或“某某弧与某某线相切”等）时，可用“反折叠”思路解决问题。

学会解题的过程就是学会处理条件的过程。以上三种策略概括了解“折叠问题”的三种思路，在解答折叠问题时，往往会遇到勾股定理、全等以及相似的知识。同时需要学生能直观想象出折叠这一过程，在脑海中复原，找到折叠前后的变量与不变量，注重探究过程，培养逻辑推理能力，使学生逐渐掌握折叠这类问题的实质，这需要教师在教学过程中始终坚持。

[参考文献]

[1]刘强.中考试题中的折叠问题[J].中小学数学（初中版），2014（06）.

[2]朱秀娟.解读图形折叠，探讨突破策略——以图形折叠专题为例[J].数学教学通讯，2019（26）.

[3]吴俊.关于初中数学教学中折叠问题的解题探讨[J].数学大世界（上旬），2019（02）.

（作者单位：镇江第一外国语学校，江苏 镇江212000）