混浊水域多波束反向散射强度传播损失改正
2020-06-03付桂合马鑫程冯成凯阳凡林
付桂合, 马鑫程, 冯成凯, 印 萍, 梅 赛, 阳凡林,
(1. 山东科技大学 测绘科学与工程学院, 山东 青岛 266590; 2. 中交公路规划设计院有限公司, 北京 100088;3. 青岛海洋地质研究所, 山东 青岛 266071; 4. 自然资源部海岛(礁)测绘技术重点实验室, 山东 青岛 266590)
多波束声呐(multibeam sonar)是目前使用最为广泛的海洋测量仪器之一, 不仅能够获得水深数据,还能够获得反向散射强度(backscatter strength, BS)。反向散射强度经过一系列的处理后, 可以绘制海底声呐图像, 为海底底质分类、海洋目标探测、海洋环境调查等诸多领域提供基础数据支撑[1-2]。多波束反向散射强度用于定量描述目标反射特性, 不仅受海底底质的影响, 而且还依赖于仪器特性及海洋环境[3-4]。多波束回波数据处理过程中, 去除海洋环境影响尤为重要, 海洋中的诸多因素都对声信号的传播产生影响, 这些因素主要包括声速剖面、水体温度、水体盐度、压强以及悬浮颗粒物等[5-6]。
国内外学者[7]都已展开多波束回波声传播损失的研究, 现有的反向散射强度传播损失改正方法主要有多波束换能器增益处理和声学模型后处理, 多波束换能器增益是通过时间变化增益(time varied gain, TVG)减少传播损失的影响, 唐秋华等[8]分析了强度数据获取过程中系统进行的实时补偿。Beaudoi等[9]分析了多波束系统换能器接收增益对回波强度值的影响, 声学模型法主要是通过声传播公式推导回波强度与海洋环境参数的关系, 彭临慧等[5]研究了混浊海水对声传播的影响, Alexandre等[4]对多波束反向散射强度传播损失与海洋环境参数的关系进行了相关研究。
在近岸河海交汇处, 河流携带大量的泥沙汇入海洋, 产生大片混浊海域。混浊海水中的悬浮颗粒物,通过热传导以及黏滞作用导致声波衰减, 对多波束声呐系统的工作性能产生显著影响, 降低了声呐的识别能力。因此研究混浊水域中的多波束传播损失成为关键问题。波束传播损失与波束的传播路径密切相关, 未考虑声速剖面对波束传播路径的影响。而传统的传播损失与波束的传播路径密切相关, TVG改正方法忽略了海水介质中环境参数的动态性, 而传统的多波束传播损失声学模型通常只考虑了纯净海水黏滞性对波束传播的影响[10], 未考虑混浊海水中悬浮颗粒物对海水黏滞性的影响, 在复杂海洋环境下适应性较弱, 改正效果不理想。
针对上述问题, 本文从声学机理出发, 考虑混浊水域中悬浮颗粒物对黏滞吸收的作用, 提出了混浊水域多波束声传播损失改正模型, 针对海洋环境参数的动态性, 对每个波束分层计算传播损失, 最后将各层传播损失累计, 获得每个波束的传播损失。
1 多波束传播损失影响因素
1.1 声传播基本原理
波束发射后, 经海水传播, 再到接收的整个过程形成了声呐方程。声呐方程的影响因素主要包括声传播介质、海底及水体目标、背景干扰和声呐参数。图1展示了波束信号从发射到接收的过程, 图1中各个参数表示如下: SL为多波束系统的声源级;TL为波束的传播损失; TS为目标强度; A为声照区面积; EL为回波能级; NL为海洋环境的声噪水平; A/D为模数变换; Dt和Dr分别发射和接受指向性; 为 Gb为ADC阶段之前实施的增益; Ga为ADC阶段之后实施的增益; RL为系统增益之后接收回波能级。BSB为海底反向散射强度。则声呐方程可表示为[10]:
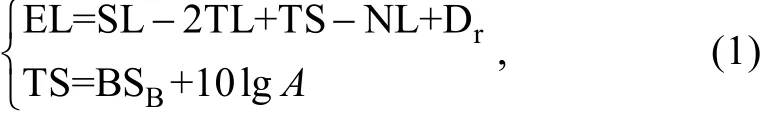

图1 多波束声呐信号流程图Fig. 1 Diagram of multibeam sonar signal flow
因此根据声呐方程, 影响海底固有反向散射强度 BSB的因素主要有 SL、EL、TL、NL、Dr等。传播损失 TL定量描述了声波传播一定距离后声强度的衰减变化, 传播损失由扩展损失和吸收损失两部分构成, 图2展示了影响传播损失的主要因素。扩展损失是由声波本身的传播特性决定的, 声波在传播过程中波阵面不断扩大, 单位面积能量减少, 衰减的速率与波阵面的表面积成正比。对于多波束声呐系统发射的球面波, 其衰减的速率与传播距离平方成正比[11]。吸收损失的本质是声传播过程中部分声能转化为其他能量(如热能), 且不可逆, 主要包括化学弛豫吸收和黏滞吸收, 弛豫吸收是指海水中的分子在声波作用下发生离解和缔合, 消耗声波的能量,黏滞吸收是由于惯性黏滞作用将速度梯度能量转化为热能而产生的能量损失[12]。

图2 影响传播损失主要因素Fig. 2 Main factors affecting transmission loss
1.2 常用传播损失改正方法
1.2.1 TVG改正
在水深测量过程中多波束系统会自动添加固定增益(Fixed Gain)及时间变化增益, 即根据信号发射后的时间长短对返回信号进行放大处理[7]:
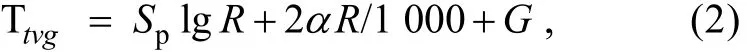
式中, α为吸收系数(dB/km), R为斜距(m), Sp为扩展损失系数, G为固定增益。
时间增益是另一种形式的传播损失改正, 吸收系数α和传播损失系数Sp是用户在进行初始设置时输入的参数值, 与测区真实的吸收系数是不同的,存在着一定的不确定性和局限性, 因此需要对采集到的回波强度进行去除TVG改正, 在数据后处理中重新计算传播损失。
1.2.2 声传播损失计算模型
传统的多波束声传播损失由两部分组成, 一部分是由波束波阵面随距离扩展产生的声强衰减(扩展损失), 一部分是由水的黏滞性和水中二价盐等化学弛豫过程引起的声强衰减(吸收损失)[10]:

式中, R为射程(m), α为吸收系数(dB/km)。α是声呐频率 f和传播介质特性(盐度、温度、深度和pH值)的函数[13]:

式中, f频率(kHz)、T为温度(℃)、S为盐度和 Z为水深(km), c为声速(m/s), pH值为7.6~8.2级, A1和A2两项表示由硼酸和硫酸镁引起的弛豫衰减。A3项表示由纯水中的黏性引起的衰减。
2 混浊水域声传播损失模型与改正
在进行多波束反向散射数据处理时, 发现根据传统方法处理的结果中反向散射强度值随传播距离的增大而减少, 这是由于传统的改正方法未考虑混浊海水中颗粒物对传播损失的影响, 没有完全去除传播损失。因此, 如何处理悬浮颗粒物对吸收损失的影响是混浊海水传播损失计算的关键。本文从声学机理出发, 重新构建了多波束声呐数据吸收损失计算模型, 使用水体温度对海洋环境参数进行自适应分层, 然后基于声速, 对每个波束分层计算吸收系数和传播距离, 最后将各层传播损失累计, 得到每个波束的传播损失, 改正流程图如图3所示。
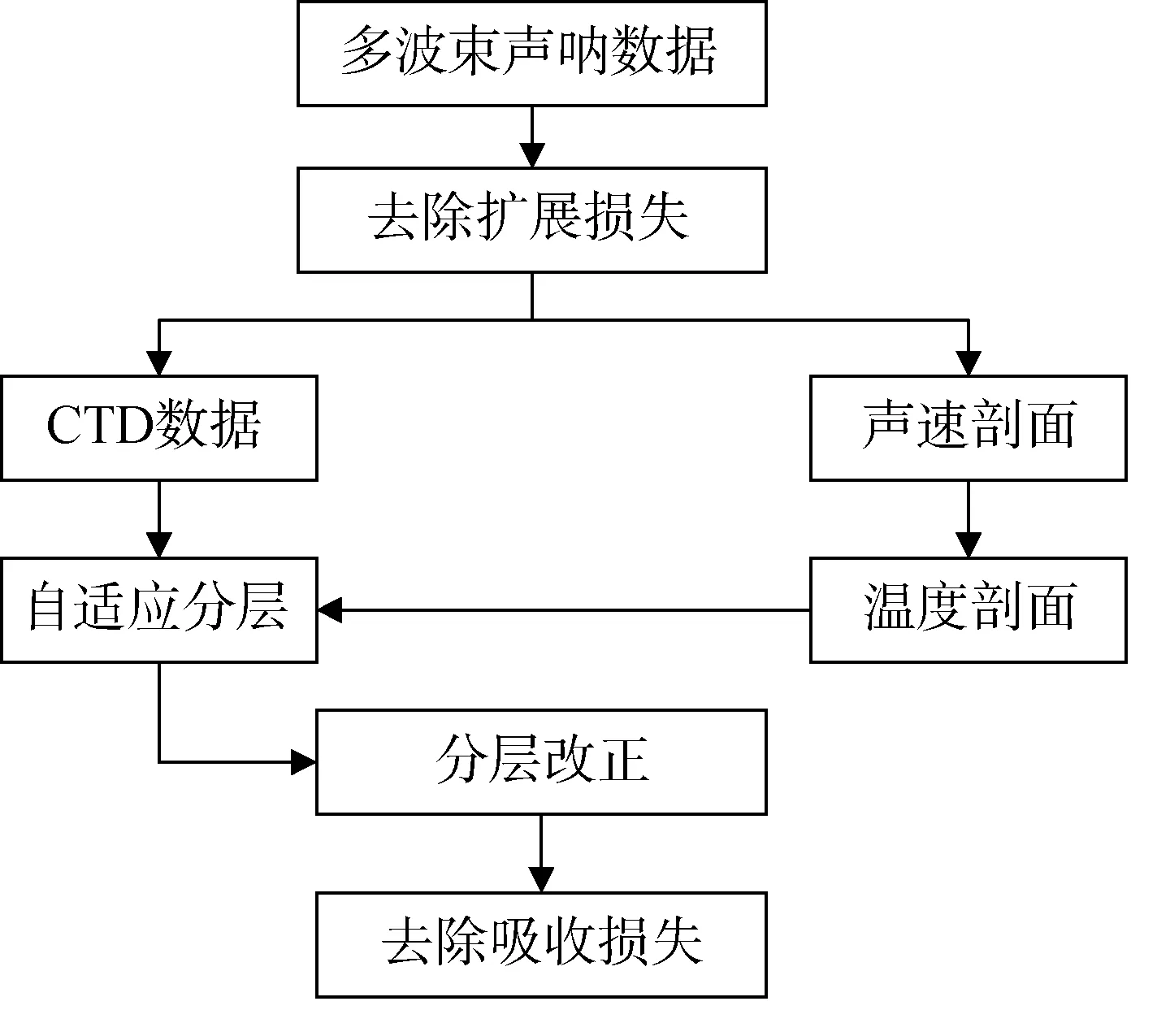
图3 多波束传播损失改正流程Fig. 3 Multibeam propagation-loss correction process
2.1 声波传播损失模型改正
相较于清澈海水, 混浊海水含有大量的悬浮颗粒物, 影响海水的黏滞性。为此, 本文算法中根据海水混浊程度重新计算黏性引起的衰减αv[14]:

式中, ε=M/ρ′是粒子的体积分数, M为悬浮颗粒物的质量浓度; k=ω/c是波数; c是海水中声速; δ=ρ′/ρ是泥沙颗粒密度与液体密度之比。α是粒子的半径;是黏滞剪切波的透入深度的倒数; ω是圆频率; v是液体的动黏滞率。
从式(5)中可以看出, 黏滞声吸收无法通过水体温度、盐度、深度直接获得, 但可以通过海水动黏滞率与水体温度、盐度、深度建立关系[15]:
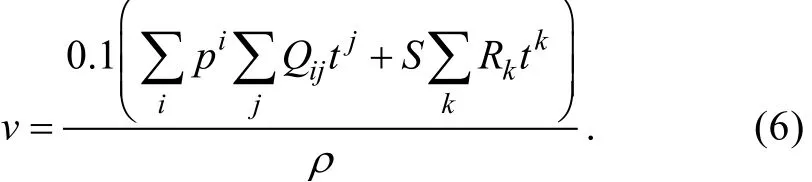
考虑海水中悬浮颗粒物造成的黏滞损失, 综合考虑式(4)中的扩展损失、弛豫损失, 则改进的传播损失声学模型为:

式(7)中, 第一项为扩展损失, 第二项为海水中分子弛豫衰减损失, 第三项为海水黏滞声吸收损失。
2.2 分层计算传播损失
不同深度的海洋环境参数常不相同, 而这些海洋环境参数对多波束反向散射强度传播过程的吸收损失有着直接的关系, 如果使用统一的系数进行计算, 会增加误差。因此, 需根据不同深度的海水参数,对水体进行分层, 计算声线路径上变化的吸收系数,依次计算每层的传播损失, 直到到达水底, 获得累计吸收损失。首先根据水体温度剖面对波束路径进行分层, 然后利用各层的海洋参数计算传播距离与吸收系数, 计算每一层的吸收损失与扩展损失, 最后获得累计的传播损失。
温盐深培面仪(Conductivity-Temperature-Depth profiler, TCD)或声速剖面仪可获取不同深度海洋环境参数, 现场实测的数据往往采样间隔较小, 获取数据较多, 就浅水多波束系统而言, 多波束每秒能够发射几十次声脉冲(Ping)数据, 每Ping数据中包含几百个波束, 如果采样间隔过小, 算法运算量较大,对计算效率提出了很高要求, 因此, 需经过数据合理筛选才能使用。仅凭经验等距离进行分段划分, 缺乏分层合理性的判断依据。本文在道格拉斯(Douglas-Peucke)算法[16]基础上, 提出一种适用于多波束传播损失改正的自适应分层方法。
图4表示的是2016年4月于浙江舟山海域部分实测温度和盐度剖面数据, 水深在30 m左右, 由图中可以看出, 盐度的变换范围在 0.5, 对声速影响较小, 因此, 本文算法只考虑使用水体温度进行自适应分层, 具体过程如下:
(1) 利用仪器采集到的数据往往是按等深度间隔分布, 可将离散温度剖面数据表示为(Ti, Di), i = 1,2, …N。
(2) 如图5所示,选取温度剖面第一个点(T1, D1)和最后一个点(Tn, Dn), 将两端点连成一条直线, 计算声速剖面曲线上各离散声剖点(Ti, Di)到该直线的距离 Zi,设定阈值为 δ, 若{Zi}max<δ, 则保留两端点舍去所有中间点, 若{Zi}max≥δ, 则保留温度剖面中到直线距离最大的中间点, 并以该点为基准将温度剖面分为两部分。
(3) 对上述两部分数据重复过程(2), 直到没有点被舍去为止, 最终将结果分为自适应分层的节点。
声速剖面是水深测量不可忽略的环境变量, 在进行声速测量时, 一些类型的仪器, 直接利用水柱测量声速, 只记录声速和对应的深度, 无法直接获得盐度和温度数据。对于水深测量, 此种类型的数据是有效的。但是对于反向散射强度测量, 需要使用温度和盐度计算吸收系数剖面。

图4 温度与盐度剖面Fig. 4 Temperature and salinity profiles

图5 自适应分层示意图Fig. 5 Diagram of adaptive layering
为了克服缺乏温度和盐度信息数据的问题, 在上述内容中提到, 在进行浅水区域测量时, 盐度变化较小, 水体中声速随温度、盐度以及深度的变化而变化, 利用这种相关性可以建立声速经验模型, 在浅水区域, 可以通过式(9)间接确定声速[17]。假设盐度在空间或调查时间内没有显著变化, 使用一定区域内的平均盐度, 根据声速剖面数据和声速经验模型, 得到不同深度的水体温度, 随后使用水体温度进行自适应分层。为验证声速构建吸收系数剖面的精度, 分别使用CTD水体温度数据和声速剖面数据构建了吸收系数剖面, 从图6中可以看出, 声速和CTD数据获得吸收系数剖面在浅水区域整体趋势相同,对传播损失的改正影响较小。
多波束测量中, 波束发射存在着一定的角度,波束通常为非垂直入射, 不同海洋环境下的传播路径完全不同。如果认为声线在水柱中按直线传播, 使用表层声速和旅行时间计算传播距离, 则无法真实还原声速传播路径。
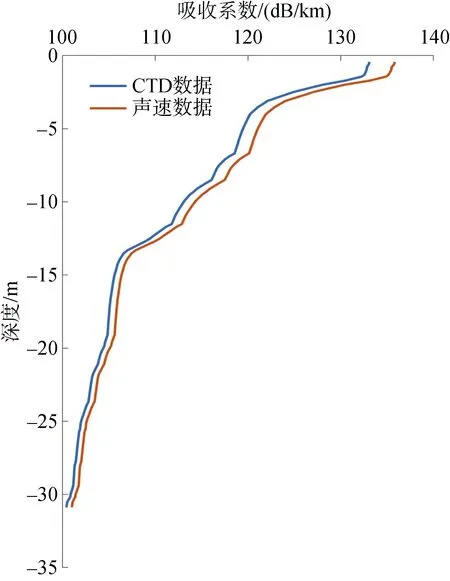
图6 不同数据构建的吸收系数剖面Fig. 6 Profiles of absorption coefficients based on differentdata
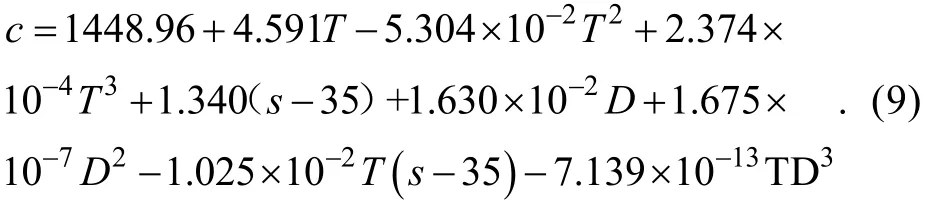
本文在常梯度声线跟踪算法的基础上[10], 使用自适应分层的节点, 沿波束传播路径逐层计算传播距离与传播损失。具体每个波束传播损失计算如下:
(1) 根据不同深度的海洋环境数据获得吸收系数剖面;
(2) 从换能器表面开始追加水层, 计算每个层的传播时间和传播距离;
(3) 累计各层的传播时间和传播损失, 累计时间与波束的实测时间比较, 并判断是否追加水层。若时间相同, 则累计的传播损失即波束传播损失, 若累计时间小于实测时间, 回到步骤(2)。若累计时间大于实测时间, 则多追加了传播损失, 需计算多余的传播损失:

式中, α′为层内吸收系数, c′为水层下界声速, Δt′为累计时间与实测时间差值。当测量深度大于获得的声速剖面深度时, 没有海洋环境参数数据, 则利用最后一层数据计算多余部分。
3 实验与分析
为验证本文算法, 选取2016年4月于浙江某海域部分实测多波束反向散射数据进行分析。采用R2 Sonic2024多波束测深系统, 其波束开角为 120°,声呐频率为400 kHz, 波束个数为256个, 实验区水深为20~30 m, 位于长江入海口, 大量泥沙流入海中,故海水混浊。
为减少深度对强度的影响, 实验选取深度较为均匀的3条相邻测线, 利用图3所示算法流程进行了传播损失改正。为便于比较, 选取未经传播损失改正、TVG改正及传统声学模型改正与本文算法处理结果进行对比分析。在实际处理中, 由于原始反向散射强度数据存在随机误差, 故对连续 Ping的反向散射强度取平均, 对数据进行平滑, 消除随机误差影响。将获得CTD数据按照水体温度进行自适应分层,设定阈值为0.2, 3条测线总共有370万个波束, 对每个波束分层改正传播损失。对原始数据进行声呐参数、声照区面积、入射角效应改正, 保证剩余数据主要受传播损失的影响。
3.1 实验结果
对处理后的 3条测线数据进行地理编码, 得到测区海底多波束声呐图像(图 7)。从图 7a可以看出,传播损失对回波强度有较大影响, 声呐图像呈现整体的不均衡性, 很难直接进行底质分类。TVG改正后, 一定程度上去除了传播损失, 但中央区域存在“亮线”, 仍有明显的拼接痕迹; 从图7c中可以看出,经传统模型改正后, 整体声呐图像较为均衡。为了更好地对比, 提取图7中红色方框区域数据, 得到传统模型和本文算法改正局部区域效果图(图 8), 从图 8中可以看出, 经传统模型改正后, 仍然可以看到测线边缘的痕迹; 经本文算法处理后, 有效去除了传播损失, 声呐图像清晰, 测线过渡自然。
3.2 实验分析
由声呐方程可以看出, 回波强度EL是目标强度与传播损失的组合, 若传播损失改正不完全, 强度数据会与传播距离有一定的相关性。Spearman等级相关系数[18]可以评价两个统计变量的相关性, 可以很好地检测变量间变化趋势的相关性:
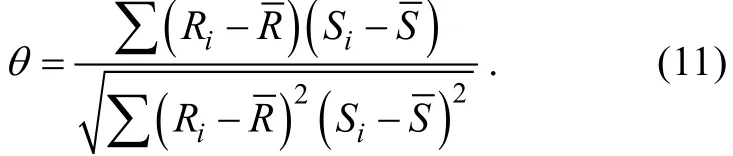
Spearman等级相关系数值越接近0, 说明反向散射强度与传播距离的相关性越小, 进而说明传播损失效果越好。提取上述测区中部分反向散射数据, 具体位置为图7中红色方框所选区域, 计算出反向散射强度和传播距离的 Spearman等级相关系数绝对值, 数据改正前、TVG改正、传统模型改正和本文算法改正的Spearman相关系数分别为0.93、0.74、0.44和0.04。通过比较发现, 本文方法 Spearman等级相关系数绝对值最小, 说明本文方法传播损失改正效果最佳。
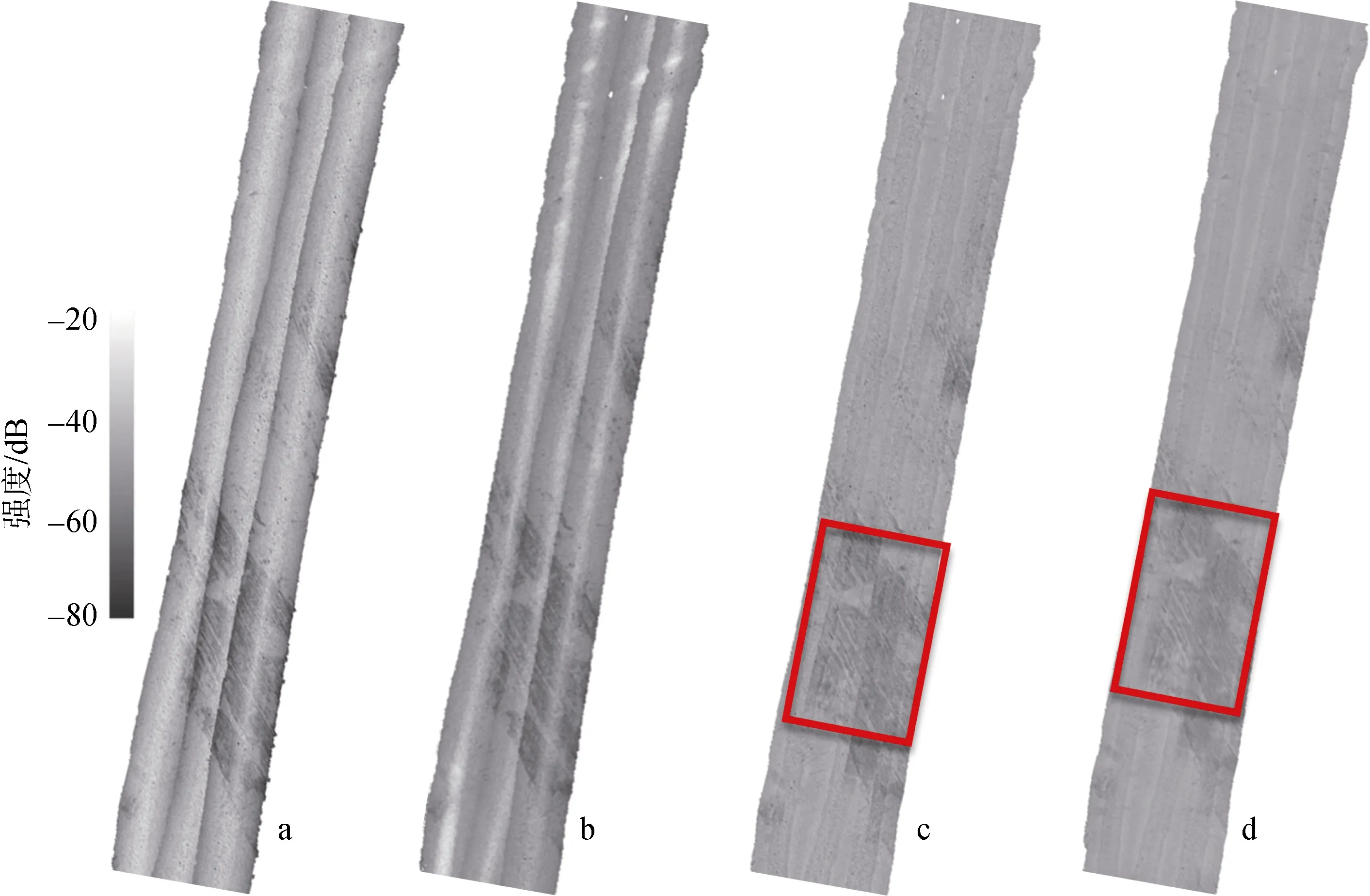
图7 不同方法效果对比Fig. 7 Comparison of the effects of different methods

图8 传统模型和本文算法改正局部区域效果图Fig. 8 Local area effects of the traditional model and this algorithm
为直观表达, 绘制出强度数据散点图, 并拟合其趋势线, 结果如图9所示。从图中可以看出,3种方法均在一定程度上去除了传播损失。由于TVG改正固定声波吸收系数, 反向散射强度仍与传播距离有很大的相关性; 相较于 TVG改正,传统声传播损失计算模型对于传播损失的去除效果较好, 但由于未考虑悬浮颗粒物对传播损失的影响, 随传播距离的增大, 仍具有一定的误差; 本文算法趋势线基本呈直线, 传播损失去除效果最好。

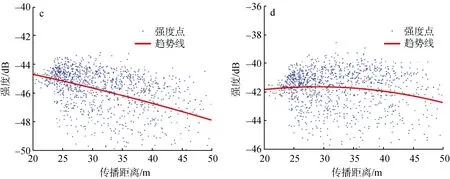
图9 不同算法的传播损失去除效果Fig. 9 Effects of the transmission-loss removal by different algorithms
4 结论
本文综合分析了混浊水域对多波束声波传播的影响, 提出了混浊海水传播损失改正的方法。通过分析混浊水域悬浮颗粒物对传播损失的影响, 对传统的声学模型进行了改进。并通过实验分析验证了该方法的有效性, 可得到以下结论:
1) 通过对实测数据进行处理分析, 有效去除了多波束回波强度的传播损失, 解决了其造成声呐图像整体明暗不一的问题。经本文算法处理后, 反向散射强度与传播距离拟合趋势线基本呈直线, 反向散射强度与传播距离的相关性明显降低, 海底声呐图像清晰, 满足工程实际需要。
2) 由于声学模型改正方法需要不同深度的海洋环境参数或声速, 并且需要分层计算, 若不能有效减少分层, 计算量较大。本文算法根据水体温度数据进行自适应分层, 在保证精度的情况下, 提高了运算效率。
3) 基于声速, 准确还原波束的传播路径, 并沿波束传播路径分层计算传播距离与传播损失, 大大提高了传播损失的计算精度。
