国产结构用铝合金断裂韧性参数校准
2020-06-03张超众郭小农宗绍晗陈宇朱劭骏
张超众,郭小农,宗绍晗,陈宇,朱劭骏
(同济大学 土木工程学院,上海200092)
铝合金材料具有轻质高强、可模性好、延展性好、耐腐蚀性好等优点,被越来越广泛地应用于现代结构工程领域,尤其是大跨度空间结构领域[1-2].断裂破坏是铝合金结构的一种主要失效模式,节点或构件的断裂失效可能导致结构发生整体倒塌[3],因此,有必要对结构用铝合金的断裂行为进行深入研究.
铝合金的断裂行为属于典型的韧性断裂.金属材料的韧性断裂理论从裂纹产生和发展的微观机制出发,可以较为准确地描述材料的宏观断裂行为,具有良好的适用性.单调荷载作用下,应用较为广泛的断裂预测模型主要有Kanvinde等[4]提出的空穴增长模型(Void Growth Model,简称 VGM)以及 Hancock等[5]提出的应力修正临界应变模型(Stress Modified Critical Strain model,简称 SMCS).基于上述模型,国内外学者对建筑钢材的断裂行为进行了广泛研究[6-15],结果表明,单调荷载作用下,VGM和SMCS模型可以准确预测钢材的韧性断裂,并可应用于钢结构节点的断裂预测.VGM和SMCS模型在钢结构中的应用已较为成熟,而对于国内建筑结构常用的铝合金材料,其研究应用却几乎为空白.铝合金与钢材相比,材料微观结构有所不同,其延性较差,韧性断裂行为可能会存在一定差别.上述断裂预测模型能否有效应用于铝合金结构,还需进一步通过试验验证.
基于以上研究不足,本文选取国产6061-T6、6082-T6和7020-T6牌号的铝合金,加工了9个标准圆棒试件和18个缺口圆棒试件进行单轴拉伸试验,并结合有限元软件ABAQUS进行数值模拟,校准了不同牌号铝合金的VGM和SMCS模型韧性参数.
1 金属材料韧性断裂预测模型
Rice等[16]首先推导了单个圆柱形或球形空穴在理想弹塑性材料中的空穴增长公式,指出空穴半径增长率与应力三轴度和塑性应变有关.其表达式如下:
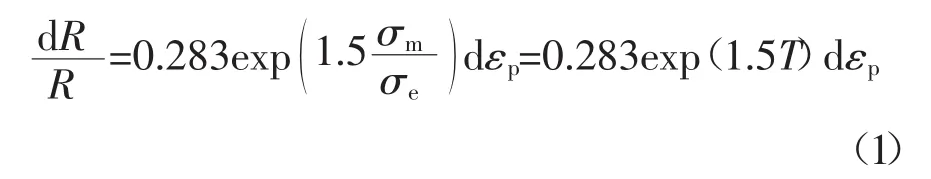
式中:R 为空穴直径;T 为应力三轴度,T=σm/σe;σm表示静水应力,σm=(σ11+ σ22+ σ33)/3,σ11、σ22、σ33分别为3个主应力;σe表示Mises等效应力;εp表示等效塑性应变.
Kanvinde等[4]在此基础上进一步提出了描述金属材料韧性断裂机理的空穴增长模型,该模型认为当应力应变历史的积分达到临界值η,即断裂指标IF,VGM≥0时,材料发生启裂,其表达式如下:

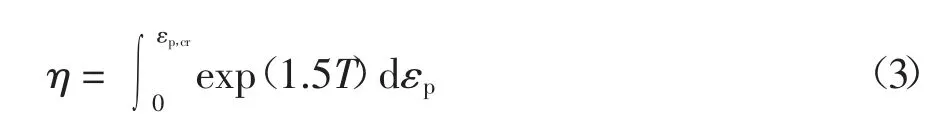
式中:η表示材料韧性参数,为材料固有属性,可通过缺口圆棒试件的单轴拉伸试验获得;εp,cr为启裂时的临界等效塑性应变.
VGM模型中包含了材料应力应变历史的显式积分,求解过程较为复杂,不利于实际应用.而Hancock等[5]研究表明,单轴荷载作用下,材料的应力三轴度在加载过程中变化较小.因此,为简化计算,将应力三轴度作为常数从积分符号中提出,得到应力修正临界应变(SMCS)模型,表达式如下:
式中:α为材料韧性参数,含义与VGM模型中的η类似;IF,SMCS为断裂指标,当金属材料在荷载作用下的等效塑性应变达到临界等效塑性应变,即断裂指标 IF,SMCS≥0 时,材料点发生启裂.
SMCS模型忽略了应力三轴度随等效塑性应变的变化,临界塑性应变取决于启裂时应力三轴度的值,而没考虑加载历史的影响.因此,与VGM模型相比,SMCS模型计算精度稍差,不适用于材料塑性变形较大(即应力三轴度变化较为剧烈)的情况.但在工程应用中,SMCS模型不需要积分,计算简便快捷,并且与试验结果吻合较好.
2 试验方案
为了研究VGM和SMCS模型用于国产结构用铝合金断裂预测的可行性,本文首先进行标准圆棒的单轴拉伸试验,以便在进行有限元模拟时,确定试验材料的弹性模量和真实应力应变曲线等基本材料参数,使有限元结果与试验结果更加吻合.
试验材料采用国产6061-T6、6082-T6和7020-T6牌号的铝合金,每种牌号的标准圆棒试件各加工3件,共计9件;缺口圆棒试件选用3种不同的缺口半径,即R分别为1.25 mm、2.5 mm和5 mm,以在缺口处构造不同的应力三轴度.每种形式的缺口试件加工2件,共计18件.试件尺寸如图1所示,试件编号见表1.
单轴拉伸试验在同济大学航空航天力学实验室进行,加载装置为30 t的微机控制电液伺服万能试验机SHT4305,引伸计标距为50 mm,量程为40%.试验加载方式为位移加载,加载速率为0.5 mm/min.试验装置见图2.

图2 单轴拉伸试验装置Fig.2 Monotonic tensile test equipment
3 单轴拉伸试验结果
3.1 标准圆棒试件试验结果
不同牌号铝合金标准圆棒试件的破坏形态如图3所示.可以看出,6061-T6铝合金试件断口颈缩明显,呈现典型的杯锥形,试件表面出现与加载轴线呈45°的剪切唇,为延性断裂;6082-T6试件延性次之,断口处略有颈缩;而7020-T6试件延性最差,肉眼观察不到颈缩现象,断口晶粒明显,并且试验中试件断裂时伴有明显响声,为脆性断裂.单轴拉伸试件的名义应力-应变曲线见图4,相应的主要力学性能指标列于表2,包括弹性模量E、名义屈服强度f0.2、抗拉强度fu、断裂荷载Pf、标距段初始直径d0、断后直径df、断面收缩率ψ和断裂应变εf.其中,断裂应力σf采用MWA法[17]计算得到,其数据列于表3.由于每种牌号铝合金的3个标准拉伸试件的名义应力-应变关系曲线在颈缩阶段前几乎相同,为了便于与后文试验曲线拟合结果对比,对每个牌号图4仅给出了1条实测曲线.

图3 标准圆棒试件破坏形态Fig.3 Failure modes of smooth round bar specimens
采用Ramberg-Osgood模型[18]对铝合金本构关系进行拟合,其通用表达式为:

式中:E为原点切线弹性模量;K为应变硬化系数;n为应变硬化指数.本文参考文献[19],以名义应力-应变曲线上点(εd,σd)为分界点,对试验曲线分段拟合,并取εd=0.02.其表达式如下:
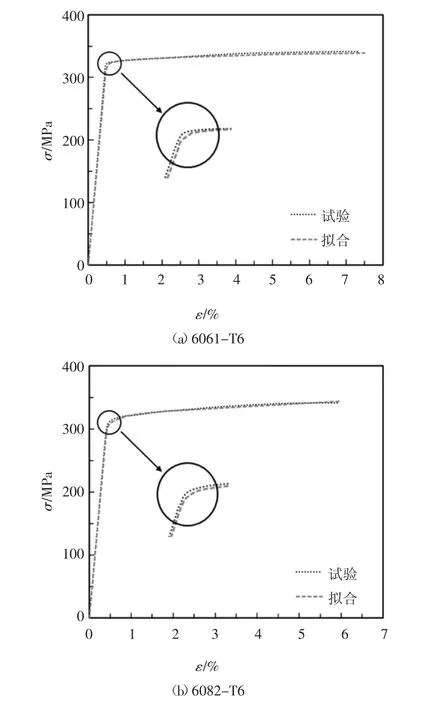

图4 单轴拉伸试件名义应力-应变关系曲线Fig.4 Monotonic tensile stress-strain curves of specimens

式中:K1为坐标点(εd,σd)右侧的直线斜率.拟合参数见表4,拟合曲线见图4.表4中,r代表曲线段的相关系数,r1代表直线段的相关系数.从图4和表4中可以看出,对于不同牌号的铝合金,试验曲线与分段拟合得到的理论曲线吻合较好,相关系数r和r1几乎都大于0.95.
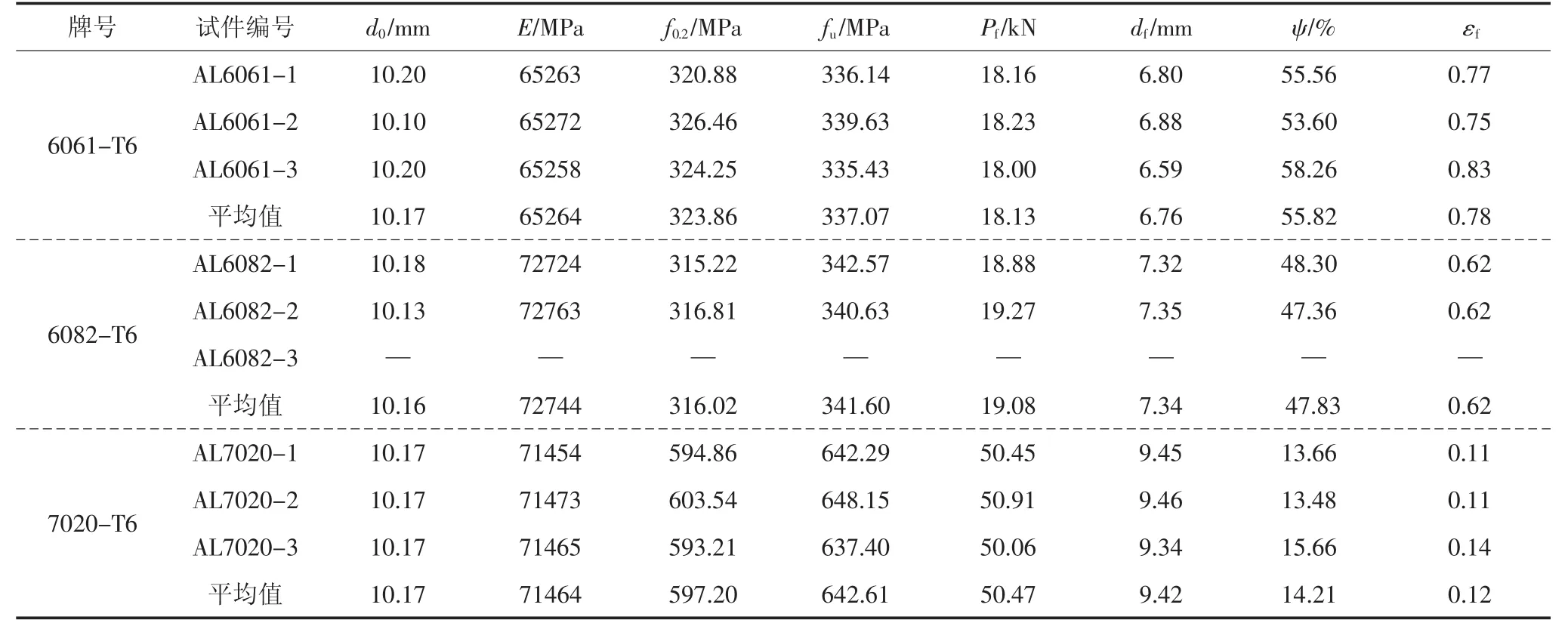
表2 标准圆棒试件单轴拉伸试验结果Tab.2 Monotonic tensile results of smooth round bar specimens
采用ABAQUS进行非线性分析需要输入材料真实应力σtrue和塑性应变,进行有限元模拟时,应使构件受拉断裂,因此本构关系需延伸至材料断裂时刻.颈缩之后的真实应力-应变曲线使用MWA法[17]进行校准,其表达式如下:

式中:σneck和εneck分别为刚开始颈缩时刻材料的真实应力和真实应变;ω是材料参数,由材性试验结合有限元模拟确定.断裂时刻的真实应变可按下式计算:

式中:d0为标距段初始直径;df为标距段断后直径.校准后材料的真实应力-塑性应变关系曲线如图5所示,关键点参数列于表4.

表3 真实应力-塑性应变曲线关键点参数Tab.3 Critical point parameters of true stress-plastic strain curve

表4 铝合金本构关系拟合参数Tab.4 Fitting parameters of aluminum alloy constitutive relation

图5 真实应力-塑性应变关系示意图Fig.5 Schematic diagram of true stress-plastic strain curve
3.2 缺口圆棒试件试验结果
不同类型缺口圆棒试件的破坏形态如图6所示,各试件均在缺口根部截面断裂.由于6061-T6铝合金延性较好,该牌号试件主要呈现出典型的杯锥状断口形态,断面不平整,具有纤维区和剪切唇区,但由于试件开有槽口,存在应力集中现象,断裂时脆性增大,因此剪切唇在试件周围不完整;对于6082-T6和7020-T6铝合金缺口圆棒试件,其延性相对较差,并且槽口处亦存在应力集中现象,因此断口表面比6061-T6试件更为平整光滑.
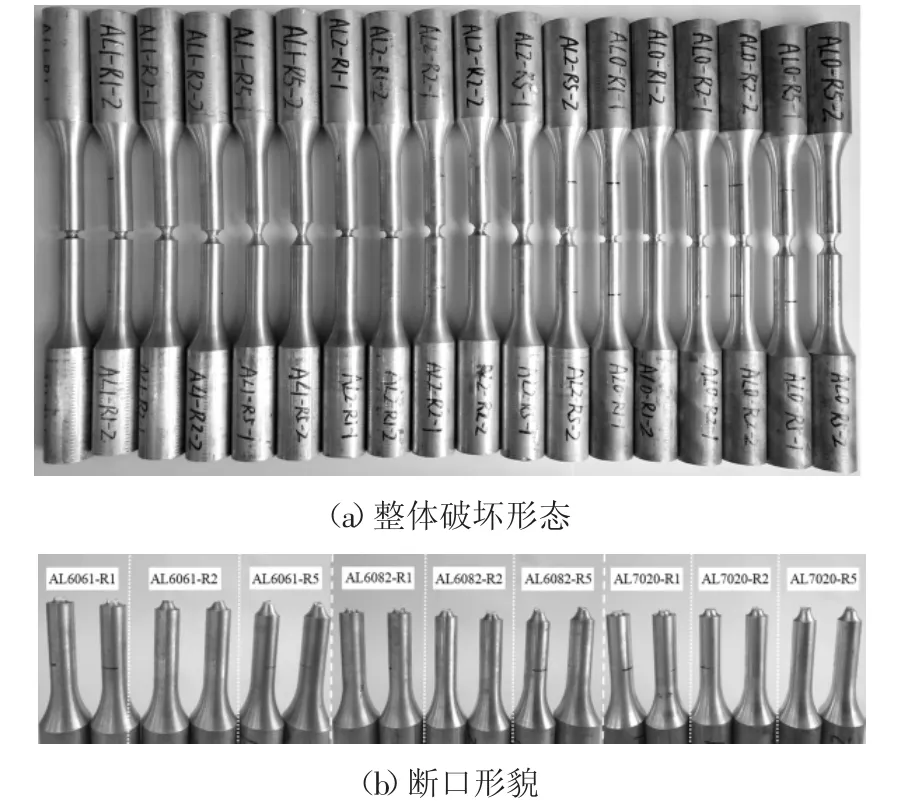
图6 缺口圆棒试件破坏形态Fig.6 Failure modes of notched round bar specimens
单轴拉伸试验得到的全过程荷载-位移曲线见图7.曲线下降段斜率的突变点为材料的启裂点,进行有限元韧性参数校准时,采用该点对应的试件标距段伸长量δf控制变形,即试件达到断裂临界状态.从图7可以看出,随着槽口半径增大,试件的名义屈服荷载和最大荷载均减小,断裂时的变形增大,说明缺口半径越大,试件塑性越好.显然,缺口半径越小,截面变化越剧烈,应力集中区域产生较高的三向同号应力,使试件破坏时脆性增大.

图7 缺口圆棒试件荷载-位移曲线Fig.7 Load-displacement curves of notched round bar specimens
4 有限元模拟
4.1 断裂模型韧性参数校准
采用ABAQUS建立缺口圆棒试件有限元模型时,根据标准圆棒试件单轴拉伸试验结果,输入材料真实应力和塑性应变.考虑到试件形状和加载方式的对称性,采用二维轴对称有限元模型(图8),单元类型为CAX4R,缺口区域单元尺寸为0.25 mm.标距段一端铰接,另一端施加强迫位移,以δf作为位移限值.有限元模拟得到的荷载-位移曲线与试验结果吻合良好,典型试件的对比结果如图9所示.通过ABAQUS输出启裂点即中心点的应力应变数据,代入式(3)和式(4),可以计算出VGM模型和SMCS模型中的韧性参数η和α.

图8 缺口圆棒试件有限元模型Fig.8 Finite element model of notched round bar specimens

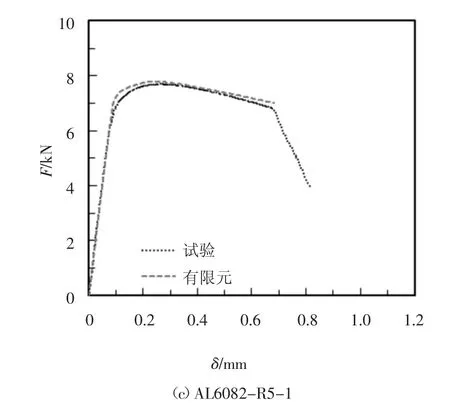
图9 试验与有限元荷载位移曲线对比Fig.9 Comparison on load-displacement curves
图10 所示为不同缺口试件达到δf时,等效塑性应变和应力三轴度沿截面直径的分布.随着试件缺口半径增大,启裂时等效塑性应变增大,应力三轴度减小.等效塑性应变变化幅度明显小于应力三轴度.启裂点位置主要由应力三轴度控制,而截面中心点应力三轴度最大,故可判断为启裂点.图11给出了启裂点处应力三轴度随等效塑性应变变化的关系曲线,可以看出,应力三轴度随等效塑性应变增加而缓慢增大,但变化范围不大,说明SMCS模型假定的合理性.
韧性参数η和α计算结果见表5.表中,Mises等效应力σe、静水应力σm、应力三轴度T及等效塑性应变εp,cr均为对应于试件启裂时的应力、应变值.由表5可知,同种牌号铝合金试件的韧性参数η和α的校准值较为一致.6082-T6铝合金韧性参数的离散性较小,离散系数在10%以内;对于6061-T6和7020-T6铝合金,由于缺口半径为5 mm的试件韧性参数明显高于另外2种类型缺口试件,导致韧性参数离散性较大,这可能是由于VGM和SMCS模型并不能完全精确地预测铝合金的韧性断裂.各种牌号铝合金SMCS模型韧性参数均略高于VGM模型,是因为在加载过程中,启裂点应力三轴度随等效塑性应变呈增大趋势(图11).
总体来说,各种牌号试件韧性参数的离散系数均在20%以内,表明韧性参数是铝合金材料固有属性,可用于试件在不同应力状态下的韧性断裂预测.不同牌号铝合金韧性参数相对大小关系为:6061-T6的韧性参数最大,6082-T6次之,7020-T6最小.

图10 等效塑性应变和应力三轴度分布Fig.10 Distribution of equivalent plastic strain and stress triaxiality
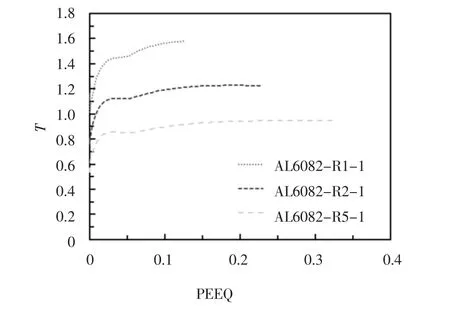
图11 不同试件启裂点应力三轴度与等效塑性应变的关系Fig.11 Relationship between stress triaxiality and equivalent plastic strain of different specimens’crack initiation point
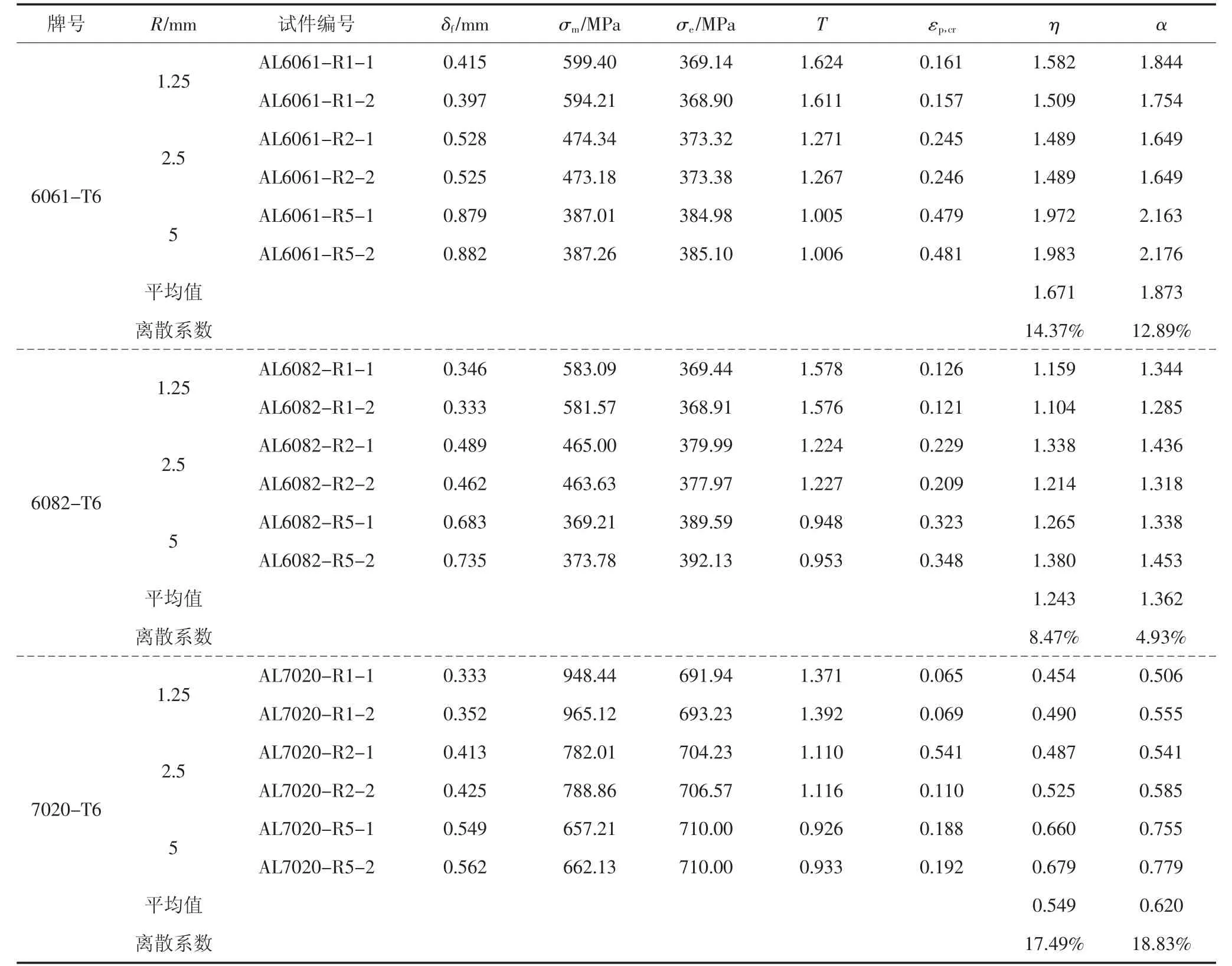
表5 VGM模型和SMCS模型韧性参数校准结果Tab.5 Toughness parameter calibration results of VGM Model and SMCS Model
图12所示为3种牌号铝合金塑性指标断面收缩率与微观模型韧性参数η和α的关系.从图中可以看出,韧性参数与塑性指标基本呈线性相关,材料塑性越好,韧性参数越大,这与文献[11-12]有相似结论.线性回归与实测数据之间的相关系数r均大于0.97,拟合效果良好.
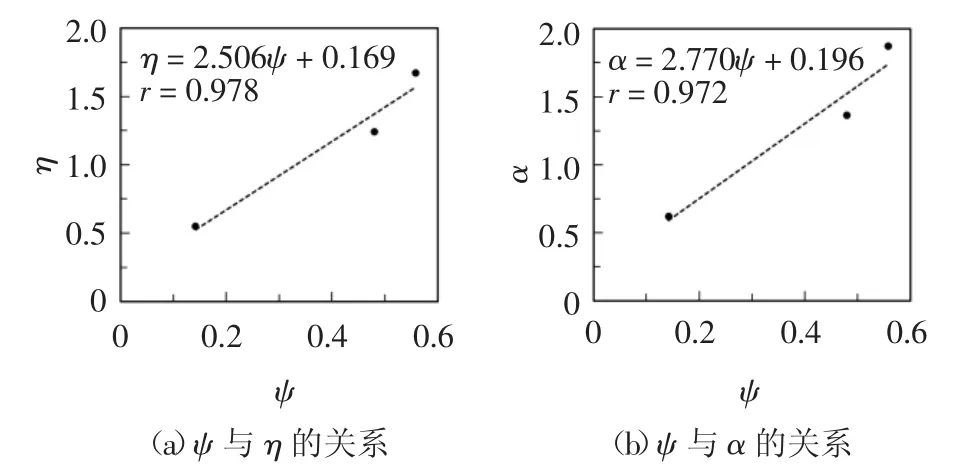
图12 铝合金断面收缩率与韧性参数的关系Fig.12 Relationship between reduction of area and toughness parameters
4.2 断裂过程模拟分析
将4.1节得到VGM和SMCS模型韧性参数η和α写入VUMAT子程序,并嵌入ABAQUS软件,可以得到试件断裂的全过程结果.图13和14所示为典型试件在变形过程中的应力云图.从图中可以看出,试件在变形为0.49 mm时于中心点启裂,随着变形增加,裂缝向截面边缘扩展,试件模拟断裂形态与试验断裂形态(图6(b))较为吻合.以VGM模型为断裂判据时,断口区域单元删除更加整齐.图15所示为有限元与试验中典型试件裂后荷载位移曲线的对比.由于VGM和SMCS模型假定断裂指标达到零时,材料单元失效,并未考虑材料损伤,而实际材料是经过损伤发展失效,因此采用上述2种断裂模型得到的荷载位移曲线达到启裂点后急剧下降.综合图13~图15分析,VGM模型能够更好地模拟试件断口形貌以及裂后路径.
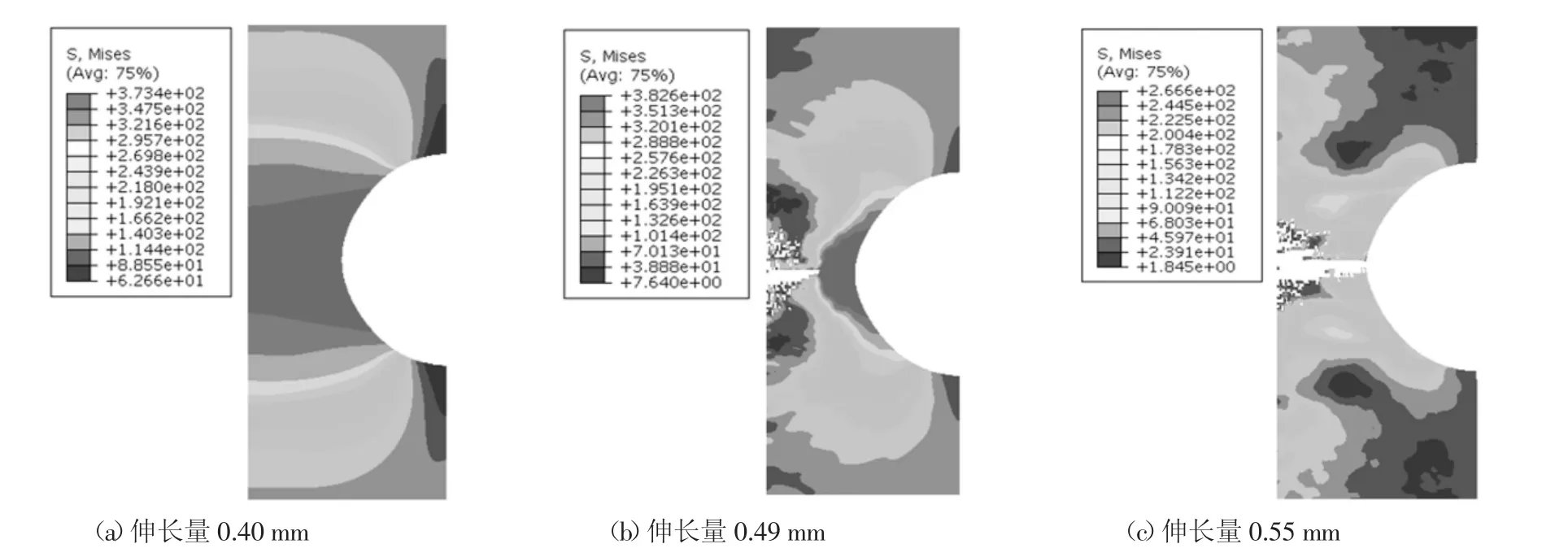
图13 AL6082-R2-1试件变形过程中应力云图(采用VGM模型)Fig.13 Stress cloud images during deformation process of specimen AL6082-R2-1(apply VGM Model)

图14 AL6082-R2-1试件变形过程中应力云图(采用SMCS模型)Fig.14 Stress cloud images during deformation process of specimen AL6082-R2-1(apply SMCS Model)
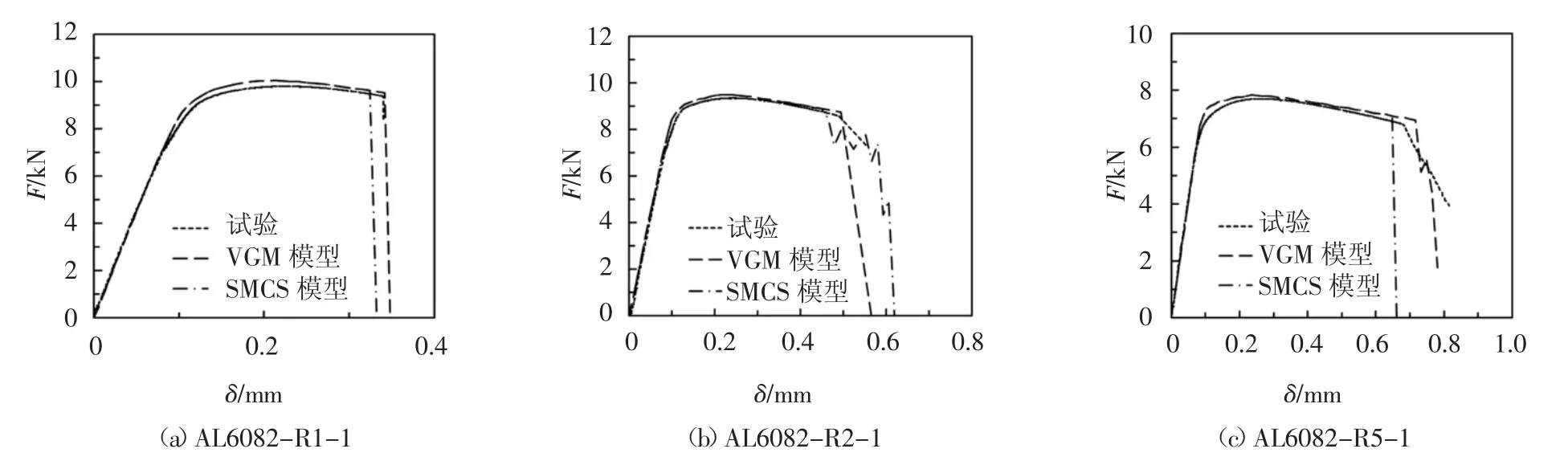
图15 有限元与试验中典型试件裂后荷载位移曲线对比Fig.15 Load-displacement comparison of typical cracked specimens between finite element simulation and test
5 结论
1)通过缺口圆棒试验结合有限元分析,校准了国产6061-T6、6082-T6和7020-T6牌号铝合金的韧性参数,有限元分析结果和试验结果吻合良好,且有限元分析表明,试件于断口截面中心点处启裂,与试验现象一致.
2)6082-T6铝合金韧性参数的离散系数为5%~9%,6061-T6和7072-T6铝合金韧性参数离散系数为12%~19%.3种牌号铝合金韧性参数离散系数均在20%以内,验证了韧性参数是铝合金的固有属性,可采用VGM和SMCS模型进行国产结构用铝合金的韧性断裂预测.
3)有限元分析表明,加载过程中启裂点应力三轴度随等效塑性应变呈逐渐增大趋势,这导致计算出的SMCS模型韧性参数稍大于VGM模型.
4)VGM和SMCS模型韧性参数与铝合金材料塑性指标断面收缩率基本呈线性相关,且相关系数均大于0.97.为方便应用断裂预测模型,可根据铝合金标准圆棒断面收缩率快捷地计算出韧性参数.
5)VGM和SMCS模型能够较好地预测国产结构用铝合金材料的韧性断裂,并且VGM模型具有更高的精度.
