基于螺旋优化的三元复合驱模糊多目标最优控制求解
2020-06-03时宇环李琦葛玉磊
时宇环,李琦,葛玉磊
(1. 中石油华东设计院有限公司,山东 青岛 266071;2. 青岛鼎信通讯股份有限公司,山东 青岛 266109)
三元复合驱是一种重要的提高采收率技术,通过在水中加入碱、表面活性剂和聚合物等,以改善流体性质,改变岩层孔隙表面物理特性,从而降低含水率,增加原油产量[1]。但是驱替剂的价格昂贵,三元复合驱往往存在投资高、风险大、开采难度大的特点[2]。因此如何科学地制定开采方案,确定最佳的驱替剂注入浓度,以最大限度地提高采收率,是当前油田研究的一大难点。
目前国内三元复合驱的方案优化主要采用指标对比法[3],该方法通过注入浓度、段塞大小等不同优化参数的组合,形成不同的注采策略,然后采用不同的策略计算模型,评价分析各个策略相应的指标,从而确定最优注采策略。该方法虽然便于实施,但是过多地依赖操作者的经验,而且缺乏严格的理论依据,很难得到最优的注采策略。最优控制是一种求解油田开发的有效方法。文献[4]采用极大值原理优化了表面活性剂驱提高原油采收率的注采策略,并根据梯度推导出最优控制存在的必要条件。但是由于油藏渗流机理的复杂性,伴随方程的计算往往十分复杂。文献[5]提出了一种混合整数迭代动态规划方法优化聚合物驱的最优注采策略,考虑了段塞大小的整数限制,实现了注入浓度和段塞大小的同时优化,目前对于提高采收率的研究大部分集中在水驱和单一化学驱,对于三元复合驱的研究还很缺乏。文献[6]提出了一种混合螺旋优化算法,通过引入柯西变异,提高了标准螺旋优化算法的全局收敛性和收敛速度,并用于求解三元复合驱的提高原油采收率问题,取得了很好的效果。但是上述方法都没有考虑多目标和生产指标的不确定性。1965年,Zadeh[7]教授发表了关于模糊集合的第一篇开创性论文,由此创立了模糊集理论和模糊数学,为模糊最优控制的求解奠定了基础。Lejeune[8]提出了一种布尔建模框架并建立了多目标金融投资优化模型,并针对该模型求解了带有变量风险集的多目标概率约束规划问题。Rashid[9]采用水平截集法,引入凸模糊集并定义了其凝聚函数子集,将模糊多目标问题转化成确定性单目标问题处理。虽然尚未有关于三元复合驱模糊最优控制问题的求解文献,但是模糊最优控制理论的发展,为求解该问题提供了理论依据。
本文针对三元复合驱生产过程中多个指标的不确定问题,提出了一种模糊多目标最优控制求解方法。首先基于三元复合驱的驱油机理,考虑多个生产指标的不确定性,建立了模糊多目标最优控制模型。其次,定义隶属度函数,描述了每个指标的不确定性,借鉴对称模型的思想和λ水平截集迭代法,提出一种将模糊多目标处理成确定性单目标问题的方法。最后采用混合螺旋优化算法求解该问题,针对三元复合驱实例,得到各个性能指标最佳结合度下的最优注采策略。
1 三元复合驱多目标最优控制模型
1.1 支配方程
三元复合驱问题的基本假设条件如下[1,6,10]:
1)地层均质,油藏等温,且吸附现象满足Langmuir等温吸附公式。
2)Darcy定律适合化学剂存在情况下的油水两相。
3)各种吸附都达到平衡,相平衡瞬间建立,且满足广义Fick定律。
4)流体和岩石微可压缩,考虑重力和毛管力的影响,忽略驱替剂对水溶液质量守恒的影响,考虑驱替剂引起的水相渗透率以及水相黏度的变化,并且考虑聚合物的不可及孔隙体积。

油相渗流方程:
(1)
水相渗流方程:
(2)
聚合物吸附扩散方程:
(3)
表面活性剂吸附扩散方程:
(4)
碱组分对流扩散方程:
(5)
初始条件:
p(x,y,z,t)|t=0=p0,
(6)
边界条件:
(7)
采出井含水率定义为
(8)
公式(1)~(8)中,井的流速项定义如下:
(9)
式中:vo,vw——油相和水相的流速;vc,vd,ve——井筒驱替剂的运移速度;vin,vout——注入井的注入速度和采出井的采出速度。方程中其他参数的含义及表达式参见文献[6,10]。
1.2 最优性能指标及控制函数
总利润最大:
(10)
总产量最大:
(11)
吨油成本最小:
(12)
总投资最小:
(13)
式中:χ——折现系数;Υo,ΥΘ——原油、驱替剂的价格系数;Υcost——单位时间的生产成本;dσ, dt——空间和时间的微元;Z——指标函数,下标R,Q,C,I分别为利润、产量、吨油成本和总投资。
对于实际的原油开采,往往存在一些模糊的生产要求。假设总利润不得低于Re,总产量不得低于Qe,吨油成本不得高于Ce,总投资不得高于Ie。要使得这几个条件同时成立,求得最优注采策略,会导致该优化问题无解,因此,要综合考虑各个目标,使得在所有目标都满足的情况下,各目标均达到相对最优水平(即各目标的最佳结合度),求得相应的最优注采策略。则模糊多目标可重新写为
(14)

油藏开采一个周期往往5~10 a,很难做到驱替液注入浓度的连续变化。因此,在工业生产中,驱替液通常采用阶梯式段塞注入方式,即配置好驱替液后在一定时间内保持浓度不变,连续注入。其具体形式可以用分段函数表示[11],即
(15)
式中: 前P个段塞为驱替液注入采油,最后1个段塞为水驱。
1.3 约束条件
驱替剂用量约束:
(16)
式中:MΘmax——三种驱替剂的总用量。
注入浓度约束:
0≤ρΘin≤ρΘmax
(17)
式中:ρΘmax——三种驱替剂的最大注入浓度。
2 基于混合螺旋优化算法的模糊多目标最优控制求解
2.1 确定性模型描述
对于第一节中以公式(14)为目标的模糊多目标最优控制问题,需要转化成确定性单目标问题才能进行求解。为了进行确定描述,为每个指标定义如下隶属度函数。
利润隶属度:
(18)
产量隶属度:
(19)
吨油成本隶属度:
(20)
总投资隶属度:
(21)
式中:Re,Qe,Ce,Ie——总利润、原油总产量、吨油成本、总投资的期望值;Rl,Ql——总利润、原油总产量的下限值;Cu,Iu——吨油成本、总投资的上限值。
为了方便模型处理,先将第一节中的多目标模糊规划中的模糊目标处理成一致的求最大值,则相应的吨油成本和总投资的性能指标以及隶属度函数可写作如下形式:
(22)
(23)
(24)
(25)
2.2 基于对称模型和水平截集的模糊多目标处理
一般在处理多目标问题时,往往采用权重法进行处理[12],即根据对每个生产指标的侧重程度,给定不同的权重,然后对加权指标求和。然而该方法往往求得的是一定综合程度上的最优解,不能得到所有指标满意度最大的解。本节中,参考对称模型的对称思想,结合模糊规划的λ水平截集的方法提出了一种将多目标模糊最优控制转化为确定性单目标问题的方法,该方法能科学地考虑各个指标,求得满足每个指标的最大满意度解。
由于在Werner的对称模型中[13],认为模糊目标和模糊约束的地位是对称的,结合该思想,该节模糊多目标规划问题只包含模糊目标,而约束都是确定的,因此通过引入权重反映对各个指标的侧重程度,将地位不均等的各个指标统一映射在对称的Werner对称模型中。结合λ水平截集[14],可以很好地避免将多目标问题转化为单目标问题。
根据各个指标的重要程度,引入权重因子wk,k∈{R,Q,C,I},则处理后重要程度相同的性能指标为wRZR(ρΘin),wQZQ(ρΘin),wCZ′C(ρΘin),wIZ′I(ρΘin)。
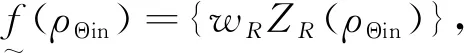
(26)
则λ水平截集迭代法的基本步骤如下:
1)任给λ(k)∈[0, 1],收敛精度ε,通常为ε=10-3~10-6,初始化k=1。

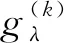
(27)
支配方程约束条件


5)收敛检查: 若|ε(k)|≤ε,收敛,转到步骤(6);若|ε(k)|>ε,不收敛,转到步骤(7)。

7)执行λ(k+1)=λ(k)-α(k)ε(k),其中0<α(k)<1,应使λ(k+1)∈[0, 1]。
8)令k=k+1,转到步骤(2)。
式(27)是一个确定性单目标最优控制问题,可用常用的约束优化方法进行求解。
2.3 混合螺旋优化算法求解
式(27)中的支配方程是关于时间和空间的复杂偏微分方程,难于用常用的优化方法进行求解,这里笔者采用全隐式有限差分法[15],对系统的状态和控制在空间和时间上进行离散。具体过程如下:
将整个空间离散成nx×ny×nz个网格,i(i=1, 2, …,nx),j(j=1, 2, …,ny),k(k=1, 2, …,nz)分别表示在x,y,z方向上的离散网格,xi,yj,zk表示在x,y,z方向上的第i,j,k个坐标值。采用块中心网格系统[16],即网格(xi,yj,zk)位于网格(i,j,k)的中心。定义xi-1/2,xi+1/2,yj-1/2,yj+1/2,zk-1/2,zk+1/2分别表示网格(xi,yj,zk)的左、右边界。为了方便描述,这里采用W={ρΘ,p,Sw}表示系统的状态,则系统的状态可以离散为
(28)
式中:n=0, 1, …,N-1——三元复合驱的时间步长;N——驱油的总步数;Δtn——第n个时间步的大小;Wn+1——tn+1时刻的状态向量;Δx, Δy, Δz——在x,y,z方向的空间步长。以x-y平面为例,定义的网格系统如图1所示。
系统的支配方程可离散化为如下一般形式:
n=0, 1, …,N-1
(29)
螺旋优化算法是由Tamura和Yasuda于2011年提出的[17],该算法是基于自然界中的螺旋现象而提出的一种全局优化算法,生活中常见的螺旋现象包括漩涡、海螺、风暴等。该算法的基本原理是: 种群个体围绕选取的最优解(即中心点)执行旋转变换操作,进而搜索全部解空间,逐步逼近最优解。螺旋优化算法能解决全局优化问题,具有较好的效果。但是当问题复杂度过大,变量空间覆盖广的情况下,该算法依然存在容易陷入局部极值、出现粒子积聚现象的问题。混合螺旋优化算法[6]通过引入柯西变异,使算法跳出局部最优值,又通过拉丁超立方采样和动态调整变异概率[18],改善了算法的局部寻优能力,具有非常好的寻优能力。

图1 块中心网络示意
采用混合螺旋优化算法优化式(27)的步骤如下:
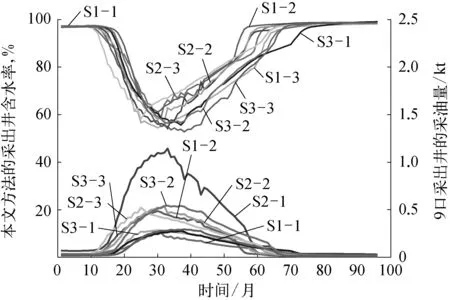
1)参数设置。设置种群大小(搜索点个数)PopSize≥2,决策变量维数n,旋转角度0<θ<2π,收缩系数0 4)旋转操作。按照多点搜索螺旋模型将各个个体进行旋转操作: ρΘin, i(k+1)=Sn(r,θ)ρΘin, i(k)- (30) 5)变异操作。根据式(31)计算变异概率: (31) 采用柯西变异对每个个体执行变异操作,式(33)为柯西变异的概率密度[19]: ρΘin, i, j(k+1)=ρΘin, i, j(k+1)+ηC(0, 1) (32) (33) 式中:μ——定义分布峰值位置的位置参数;λ——最大值一半处的一半宽度的尺度参数;kmax——最大循环迭代次数;P0,Pt——k=0和k=kmax时的变异概率。 (34) 对于三元复合驱的约束条件,次用罚函数法构造增广性能指标[20],上述求解步骤不变。 图2 井位分布示意 采用三元复合驱提高原油采收率的油藏为四注九采模型,4口注入井在中间等距分布,9口采出井均匀分布在注入井周围,每4口采出井中心有1口注入井,油藏井位分布如图2所示,其中井位号S表示生产井,井位号I表示注入井。该油藏模型按x,y,z三个方向进行网格划分,油藏长为630 m,宽630 m,厚度为19.99 m,在x,y方向等距划分为21等分,在z方向划分为7层,其中油藏每层厚度均为2.857 m,油层净厚度为1.428 6 m,油藏孔隙度均为0.3,油藏总孔隙体积为3.888 1×105m3。油藏9口生产井的采出流量见表1所列,油藏参数见表2所列。表2中具体变量定义可参见文献[10],4口注入井的注入量均为83 m3/d。从三元复合驱替剂注入时间为初始时间点,采样时间点数L=97,油藏开发持续时间为96个月,空间节点数N=21×21×7。 表1 生产井产液量 m3/d 表2 油藏参数 油藏注入策略采用三段塞,即前3个段塞为驱替液驱替,第4段为水驱。为了简化计算,设定4口注入井的注入策略相同,只优化注入浓度。油藏开发周期为96个月,共等分为6阶段,即为6个时间步,每个阶段为16个月,其中三元复合驱的注入时间共3个段48个月,每个阶段执行相同的控制策略,其中三元复合驱的注入浓度范围均为0≤ρΘin≤4 kg/m3。 模糊参数:Re=4 600万元,Qe=130 kt,Ce=450元,Ie=4 400万元,Rl=4 400万元,Ql=120 kt,Cu=550元,Iu=4 600万元。各个指标的权重为wR=0.25,wQ=0.25,wC=0.25,wI=0.25。 采用第2章所述方法求解该多目标模糊最优控制问题。假设月折现率参数α=1.5×10-3,原油价格为Po=1 800元/t,表面活性剂价格为Ps=28 000元/t,聚合物价格为Pp=25 000元/t,碱的价格为POH=5 600元/t,单位时间的生产成本为Pcos t=800元/d。 算法参数: 种群大小PopSize=20,旋转参数r=0.95,θ=π/2。混合螺旋优化算法的变异概率P0=0,Pt=0.15(kmax=1 000),收敛精度ε=10-4。 为了说明本文提出方法的效果,采用相同的段塞大小,设定4口注入井的注入策略相同,只优化注入浓度。采用指标对比法进行优化,将优化结果与本文所提方法的结果进行对比。采用指标对比法优化的注入策略为ρOHin=2.9 kg/m3,ρpin=2.1 kg/m3,ρsin=1.8 kg/m3。 优化结果如图3~6所示。图3中采用本文方法所得最优注入质量浓度为:ρOHin=(3.5, 2.6, 1.8) kg/m3,ρpin=(2.3, 1.2, 0.7) kg/m3,ρsin=(2.4, 1.5, 0.5) kg/m3。图4表示优化前基于指标对比法的生产井含水率和产油量,图5为经优化求解后的注入策略下的生产井含水率和采油量。图6表示生产井平均含水率。 图3 注入质量浓度对比示意 图4 优化前生产井含水率和采油量示意 为了直观表示优化前后驱油效果,取生产井的平均含水率如图6所示。经对比分析可知,近似动态规划求解获得的控制策略在注入前期含水率下降明显,这主要是因为在开发前期生产原油越多折算到现在的净现值越多,所以在油藏开发前期驱替剂的注入量较大,故含水率下降较快。但是,经过一段时间的开采,含水率开始上升,三元复合驱驱油效果减弱,所以注入量开始减少,含水率上升。 图5 优化后生产井含水率和采油量示意 图6 生产井平均含水率对比 在指标对比法策略下,整个过程消耗聚合物1 003.968 t,表面活性剂860.544 t,碱1 386.432 t,产油量143 624 t,净收益为3 867万元。在本文提出方法优化之后的注入策略下,共消耗聚合物669.312 t,表面活性剂653.376 t,碱1 258.944 t,产油量为138 371 t,净收益为4 725万元。采用本文方法优化之后,净收益增加了858万元,取得了很好的经济效益。 为评价算法对各个指标的权衡情况,定义违反度综合评价指标δ (35) 式中:N′——指标数;E——生产指标集合;μi——第i个指标的隶属度;w——指标权重。 为了比较模糊多目标最优控制的优化效果,分别在各个目标单独作用下,采用混合螺旋优化算法优化求解三元复合驱的模糊单目标最优控制问题,模糊多目标最优控制求解结果见表3所列,不同准则下优化的最优驱替剂最优注入质量浓度见表4所列。根据违反度评价指标可以发现,该指标越大,表明指标越符合要求,所得的最优注入浓度的满意度越大。通过对比表3中的数据可以发现,在所有优化的注入策略中,本文提出的方法(最佳结合度)得到的违反度评价指标最大,为0.238。通过对比四项模糊指标的结果可以发现,本文方法优化的结果,能得到较高的总利润和总产量,而且消耗的吨油成本和总投资较少,能在所有的模糊指标中,找到最优的结合度。因此,本文提出的模糊多目标最优控制求解算法能较好地权衡三元复合驱的各个性能指标,求出最佳结合度下的三元复合驱最优注采策略。 表3 模糊多目标最优控制求解结果 三元复合驱模糊多目标最优控制是带有不等式约束的分布参数系统模糊最优控制问题,本文提出的基于混合螺旋优化算法的模糊多目标最优控制求解方法,能很好地权衡各个模糊指标,将多目标模糊最优控制转化成为单目标确定性问题进行求解。 表4 不同准则下优化的驱替剂最优注入质量浓度 kg/m3 采用混合螺旋优化算法求解该问题,能避免利用极大值原理所导致的伴随方程的求解,易于实施。针对具体的三元复合驱提高采收率问题,进行优化求解,得到三元复合驱的最优注采策略。最后通过仿真分析验证了提出算法能在各个指标最佳结合度下得到最优注采策略。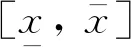
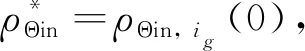


3 模糊多目标规划求解
3.1 油藏描述



3.2 仿真结果




4 结束语

