集装箱码头物流系统弹性仿真分析

王文龙 周 强 吴志福 田 宇

(武汉理工大学物流工程学院 武汉 430063)

0 引 言

系统弹性研究是现阶段复杂系统科学研究的难点问题之一.各学者对系统弹性概念的阐述、测度指标以及形式化描述方法的确定存在许多的争议.Holling[1]被认为是最早提出系统弹性的一般概念的人，其定义系统弹性是可以吸收和容纳未来事件中意外事件的一种能力.AndersonS[2]认为弹性是系统应对积极或消极影响的恢复能力和柔性的综合体现.Chri等[3]认为弹性是受到意外干扰中断后，恢复到原来或者更理想状态的能力.耿亮等[4]认为弹性是系统面对不确定风险时，吸收扰动能力、自适应力和恢复力等综合能力的体现.Woods[5]通过对其他文献的总结，针对弹性的不同用途将其定义为四个基本概念：受创反弹并恢复平衡的反弹力、与鲁棒性类似的韧性力、与脆性相反的扩展性以及最终希望达到的随外界条件变化的持续适应能力.然而目前为止，对于系统弹性的研究主要集中在供应链、计算机学、军事运筹学等领域，在物流系统弹性的研究上没有成熟的研究成果，而集装箱码头物流系统作为典型的物流系统之一，对其的弹性研究也十分罕见.

随着物流行业的快速发展，集装箱码头外部条件及内部环境也愈加复杂，系统容易被内、外部环境的不确定性所影响，干扰系统的正常运作甚至对系统本身造成危害.为了分析和建立自身性能优良、抗干扰能力强的集装箱码头，文中通过对集装箱码头进行系统的分析，结合码头的实际情况，提出集装箱码头物流系统弹性的概念，分析给出合理的测度指标，探讨合理的集装箱码头系统弹性仿真试验方法，实现集装箱码头系统弹性的定量研究，为建立性能优良、抗干扰能力强的集装箱码头提供理论指导.

1 集装箱码头物流系统的弹性基础

1.1 码头物流系统弹性的不确定因素分析

在复杂系统研究领域，国内外学者通常认为系统弹性是复杂系统应对不确定因素的主要特性.系统弹性的影响因素分为静态影响因素与动态影响因素两大类别[6-7].

1) 静态影响因素 系统弹性的静态影响因素，主要指码头的规模、平面布局、基础设施配置等.在集装箱码头内部，码头进出口大门、堆场的占地以及路网的安排，这些都是系统规模的范畴.显然，在同等的吞吐量下，规模越大的集装箱码头，其抵抗意外干扰的能力就越强.而集装箱码头在投产建成后，其平面布局也基本确定，此时系统的规模就很难产生较大变化.相较之下，码头的设备配置则灵活的多.系统内部的设备配置数量或型号发生改变，其作业能力相应产生变化，系统弹性也会随之变化.显而易见，对于同一码头，适当增加设备配置的数量或者选用更高效的机械设备，码头应对不确定干扰影响的能力会增强.但在工程实际中，系统内部的设备配置需要综合考虑码头的运营规模、生产效率、运营成本等因素，而不单单只考虑系统弹性的优劣.

2) 动态影响因素 除了静态影响因素外，弹性还与系统的作业方式、作业状态等动态因素有关.码头的堆存策略、堆存期以及不同稳态水平等都会对系统弹性产生影响.而在日常运营中，尤以系统的忙闲层度对系统弹性的影响最大.当系统处于“淡季”——低负荷稳态水平时，系统的输入输出水平(进出口集装箱量)、设备利用率都处在较低的水平，此时系统遭受意外干扰，系统本身的运输能力还有较大的“余地”，系统可以通过运用空闲设备来应对意外干扰造成的影响；而当系统处于高负荷稳态水平时，系统的输入输出水平、设备利用率已然达到较高的水准，即使是短期内的意外干扰作用，系统也可能难以承受.因此，本文将不同堆存策略、堆存期以及稳态水平等因素称为系统弹性的动态影响因素.

1.2 系统弹性的定义与性质

本文结合经典力学弹性以及弹性在其他学科的定义，深入分析集装箱码头自身相关特点，对集装箱码头物流系统弹性作如下定义：在一定稳态水平下，集装箱码头物流系统遭受外部干扰偏离初始正常稳态水平，而在外部干扰消失后通过内部调节逐渐恢复到初始稳态水平的能力.

基于上述集装箱码头物流系统弹性的影响因素分析及概念定义，总结系统弹性具有如下性质：

1) 稳态性，弹性是相对系统稳态变化的一种属性，与经典力学的弹性不同，集装箱码头的弹性不仅与系统内部的结构有关，还与外部的环境有关.外部环境的改变(例如同一码头运输量的变化)对码头系统弹性具有较大影响.

2) 弹性是系统在应对意外干扰时所体现出的性能.换言之，系统在正常运作状态下，系统弹性无法体现其作用，也就无法判断系统弹性的强弱.

3) 弹性在系统对抗意外干扰时的作用是循序渐渐的，存在既定的过程.即系统在遭受意外干扰作用时，必然要经历一系列阶段历程，各阶段会循序渐进，不会相互越级，也不会凭空消失.

4) 系统弹性的体现与意外干扰有关，干扰要使系统偏离稳态水平，但却不足以使系统崩溃.若在外部冲击下集装箱码头仍能保持作业稳态，表明意外干扰作用较小或是系统本身较强，并不能反映该集装箱码头物流系统弹性的优劣；若集装箱码头在意外干扰作用下完全崩溃而无法恢复，讨论其弹性能力也就没有意义了.

5) 系统弹性是对自身能力的体现，不单单指“弹力”.蚂蚁力气比人小，但蚂蚁能举起超出自身很多倍的重物.码头物流系统弹性亦是如此，其衡量标准是自身，即大码头的弹性不是一定强于小码头.

1.3 集装箱码头物流系统弹性的形式化描述

1.3.1弹性过程解析

弹性过程是指集装箱码头在意外干扰下先偏离稳态而后恢复稳态的所经历的整个过程.这个过程一般包含多个阶段.Abdullah等[8]将弹性过程解析为抵抗和反应两个阶段；严晓芳等[9]将按系统功能的状态将系统弹性阶段分为正常工作、部分功能丧失、主要功能丧失和系统功能恢复四个阶段；崔琼等[10]将弹性过程分为吸收阶段、自适应阶段及恢复阶段.综合各专家学者在不同领域对于弹性过程的划分，并结合集装箱码头自身特点，笔者将其弹性过程分为抵抗阶段、稳定阶段以及恢复阶段.码头系统弹性过程见图1.

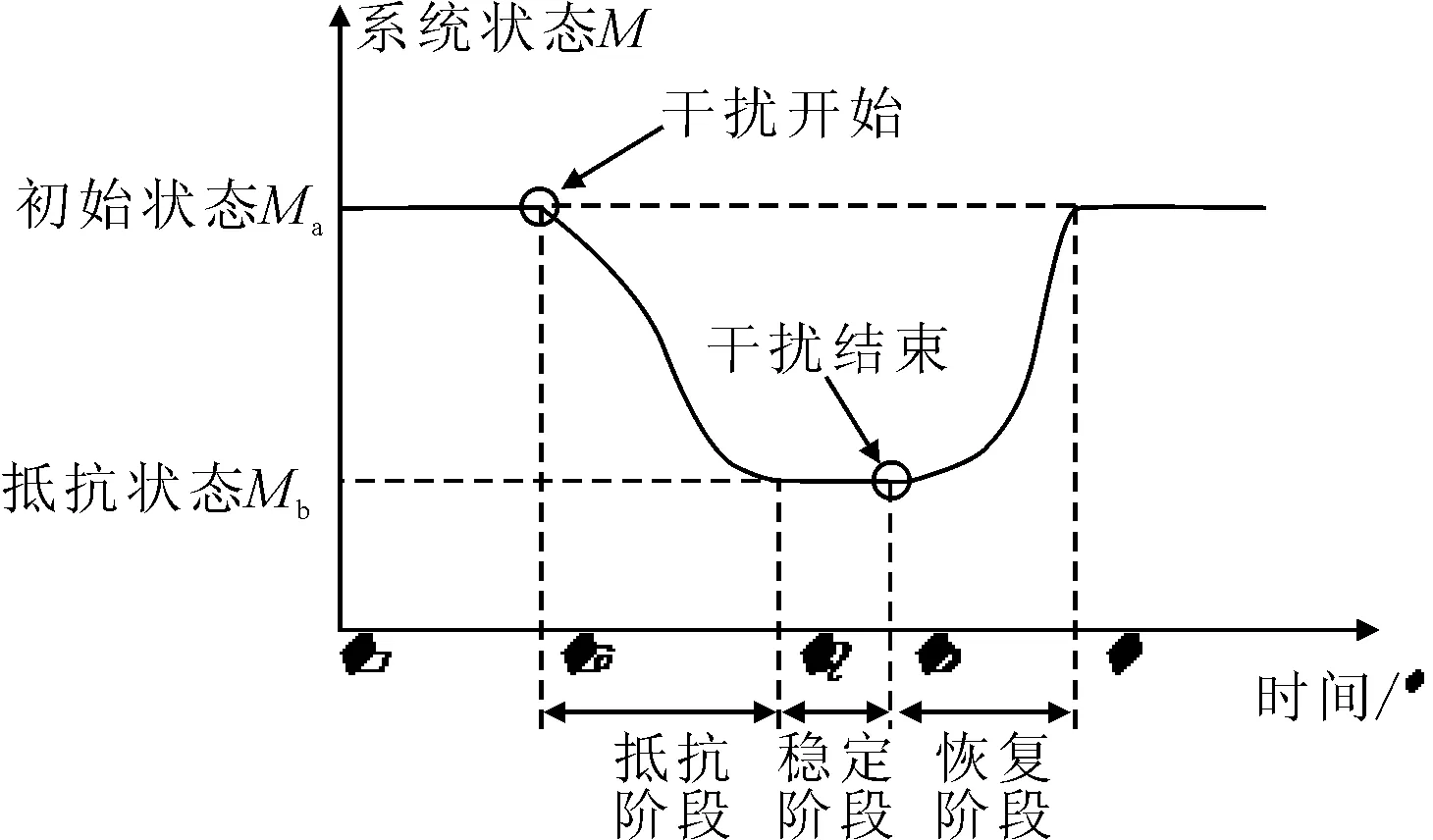
图1 弹性过程示意图

1) 在(t0，ta)期间，系统正处于初始作业稳态.

2) 从ta时刻起，系统状态开始变化，并持续远离初始状态，表明系统从ta时刻遭受到意外干扰的冲击.在(ta，tb)期间，系统正处于抵抗阶段.

3) 在(tb，tm)期间，系统在抵抗外来冲击的情况下，达到了新的稳定状态.对于集装箱码头而言，在实际情况中，这一稳态的历经时间经常为零(即tb点与tm重合).

4) 从tm时刻起，系统开始进入恢复阶段.在意外干扰冲击作用消除后，系统通过一系列策略手段进行自我调整，逐步消除意外干扰作用的影响，恢复到初始作业稳态.

对于集装箱码头而言，由于稳定阶段的历经时间经常为零，通常将稳定阶段并入到抵抗阶段分析，因而可从抵抗能力与恢复能力两个部分对集装箱码头物流系统弹性进行分析.将系统处于抵抗阶段和新的稳定阶段的时间定义为系统的顽抗时间te，即te=(tm-tb)+(tb-ta)=tm-ta.在同样的初始状态Ma和抵抗状态Mb下，te越大，表明系统能够抵抗意外干扰的时间越长，即系统的抗干扰性越强，则系统弹性越强.定义指标时间抵抗比率σa→m：

(1)

将系统处在恢复阶段的时间定义为恢复时间th，即th=ts-tm.在同样的初始状态和抵抗状态下，th越小，表明系统恢复到初始状态的时间越少，效率越高，即系统的恢复性能越强，则系统弹性越强.定义指标时间恢复比率σm→s为

(2)

为了使指标能够保持一致性，即通过定义的数学公式使得“σa→m越大，系统抵抗性能越强”，“σm→s越大，系统恢复性能越强”，定义指标：

R1=eσa→m，R2=e-σm→s

(3)

1.3.2系统状态空间

集装箱码头系统的状态变化是系统弹性产生作用的体现，就集装箱码头而言，其系统状态可以通过码头主要设备的利用率来体现.结合1.3.1对弹性过程的解析，构建码头系统的状态空间，借助向量范数理论描述系统的状态变化.综合考虑，选取仓库占用率R、泊位(岸桥)利用率F、场桥利用率V构建三维欧氏空间.系统在ta，tm，ts时刻的状态向量为

(4)

通过系统在ta，tm，ts时刻的状态向量，计算系统状态的变化率.定义顽抗阶段的系统状态变化率为ωa→m，定义恢复阶段的系统状态变化率为ωm→s.系统状态变化率计算为

(5)

(6)

在同样的初始状态和意外干扰下，ωa→m越小，表明系统的抵抗能力越强.同理，在同样的初始状态抵抗状态下，ωm→s越大，系统的恢复能力越强，定义指标：

R3=e-ωa→m，R4=eωm→s

(7)

定义系统弹性为k,该弹性为抵抗阶段和恢复阶段体现的弹性之和，为

k=R1×R3+R2×R4=eσa→m-ωa→m+eωm→s-σm→s

(8)

2 集装箱码头主要活动流程分析

由1.3可知，系统弹性作用在干扰开始直到系统恢复稳态这一系列过程，然而实际情况中，码头对外在干扰无法准确把握，对系统弹性测度的关键数据也无法统计，因而通过仿真的手段模拟整个流程，获取关键数据.

集装箱码头物流系统是典型的离散事件动态系统[11]，其基本特征是系统状态演化由事件驱动.通过对集装箱码头主要的事件活动进行说明，建立相关的概念模型和仿真模型.下面对集装箱码头集箱活动、卸船活动、装船活动以及提箱活动四个主要活动模块之间的流转关系进行说明.

2.1 集箱活动

码头收到船舶近期计划后，如果船舶有出口箱，则码头需要为出口箱预留场地用于集箱，用于出口的重箱一般在船舶到港前四天开始，船舶到港前一天截止，由外集卡运送.集箱活动各模块间逻辑关系见图2.

图2 集箱活动模块间逻辑关系

2.2 卸船活动

船舶靠岸后，进行卸船活动.卸船活动各模块间逻辑关系见图3.

图3 卸船活动模块间逻辑关系

2.3 装船活动

卸船结束后，输出参数，驱动装船工序开始工作，装船活动各模块逻辑关系见图4.

图4 装船活动模块间逻辑关系

2.4 提箱活动

卸船工作完成，当收货人要求进口集装箱整箱提运时，集装箱输运模块开始运作，运输工作由外集卡完成.提箱活动各模块间逻辑关系见图5.

图5 提箱活动模块间逻辑关系

3 基于弹性测度的集装箱码头仿真研究

3.1 仿真案例

弹性只在系统遭受外部冲击并偏离正常作业状态才能表现出来，在实际运营中很难进行测度，而采用仿真手段可以完美解决此类问题.由于集装箱码头系统是典型的离散事件动态系统，故采用离散事件仿真软件witness对集装箱码头系统进行建模分析.

以某临海港集装箱码头为实际案例进行仿真建模.码头重箱堆场装卸工艺采用岸边集装箱起重机—集装箱拖挂车——轮胎龙门起重机，并采用空箱堆高机对空箱堆场进行堆码作业.模型的基本参数如下：

选取码头两个泊位进行仿真建模，单泊位可同时容纳三台岸桥.码头布置八台轮胎式龙门起重机和九台空箱堆高机.码头采用综合式大门，有7条进大门方向的车道，10条出大门方向的车道.模型的基本数据如下：

1) 船舶计划 该码头的年吞吐量约为45万TEU，根据1年时间推算，得出船舶计划到达的时间间隔，并拟合为Tnormal分布.

2) 集装箱载类型 在45万集装箱中，TEU占40%,FEU占60.

3) 堆场容量 出口重箱堆场箱区64个，单箱区最大容量160 TEU；进口重箱堆场箱区64个，单箱区最大容量120 TEU；空箱堆场箱区27个，单箱区最大容量120 TEU.

4) 轮胎场桥 卸箱60 s/次，装箱70 s/次，根据翻倒箱.

5) 集卡参数 主干道30 km/h，其余干道15 km/h；前沿和箱区内15 km/h.集卡的装箱量分为单FEU、双FEU和单TEU三种情况.

6) 岸桥平均作业效率 卸箱：120 s/次，装箱120 s/次，每台岸桥配置五辆内集卡.

7) 码头大门服务时间 进闸口负载车辆验证时间为0.6+NegExp(0.5)、空载车辆验证时间为0.4+NegExp(0.1)；出闸口负载车辆验证时间为0.5+NegExp(0.5)、空载车辆验证时间为0.3+NegExp(0.2).

按照实际布局情况进行建模，并根据实地调研结果设置相应参数，完成后的仿真模型见图6.

图6 某临海港集装箱码头仿真模型图

3.2 试验设计与数据分析

1) 试验设计 结合上文所提集装箱码头物流系统弹性的概念定义及测度指标，以沿海码头常见自然灾害——台风作为码头的外部干扰，设计码头系统弹性仿真试验思路如下：台风到达前48 h，码头集疏运与装卸船工作均正常进行，禁止船舶靠泊；台风到达前36 h，码头集疏运工作正常进行，装卸船任务停止；到达前12 h，系统输入停止，码头进行防台工作；台风过境2～3 h后，码头集疏运、装卸船工作均恢复正常，随后逐渐形成作业高峰，最后恢复初始作业状态.在码头其他条件不变的情况下，分别设定集装箱码头的船舶到达时间符合均值为9，12，15 h的截断正态分布，仿真上述过程，统计相关数据.

2) 数据统计与分析 统计试验数据时，需要实时考察集装箱码头的堆场总箱量，即堆场占用率，分别统计集装箱物流码头受到外部干扰后恢复到初始状态所需要的时间、统计岸桥(泊位)利用率以及场桥利用率.从而完成集装箱码头系统弹性的测度.每组方案均试验9次，统计数据见表1～3.

以Tnormal(12,4,10,14,1)分布的船舶计划为例，该方案的单次统计数据见表1.

改变船舶计划到达函数的随机数流，重复该实验八次.

以Tnormal(9,4,7,11,1)分布的船舶计划为例，该方案的单次统计数据见表2.

改变船舶计划到达函数的随机数流，重复该实验八次.

表1 船舶到达间隔均值为12 h试验参数统计表

表2 船舶到达间隔均值为9 h试验参数统计表

以Tnormal(15,4,13,17,1)分布的船舶计划为例，该方案的单次统计数据见表3.

表3 船舶到达间隔均值为15 h试验参数统计表

改变船舶计划到达函数的随机数流，重复该实验八次.

综合上述统计数据，得出在不同试验条件下，各方案的时间抵抗比率σa→m，时间恢复比率σm→s，系统状态变化率ωa→m和系统状态变化率为ωm→s，结合所提出的系统弹性计算公式，进而得出集装箱码头物流系统弹性k的值，将数据汇总至见表4.

由表4可知，当集装箱码头的船舶到达时间符合均值为15的截断正态分布时，系统弹性k=1.460；当集装箱码头的船舶到达时间符合均值为12的截断正态分布时，系统弹性k=1.940；当集装箱码头的船舶到达时间符合均值为9的截断正态分布时，系统弹性k=2.163.由上表数据可知，在不改变码头内部系统配置的情况下，以船舶到达时间间隔作为弹性仿真试验的变化因子，所得结果误差均在统计学允许的范畴内，符合集装箱码头系统弹性的基本性质，也进一步验证了该弹性仿真试验方法及测度指标的科学性与可行性.

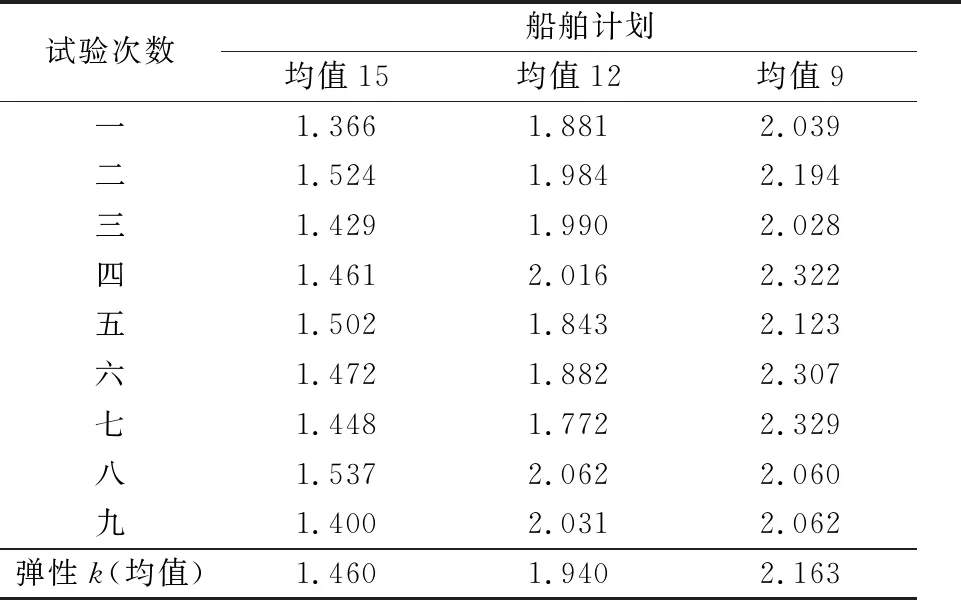
表4 试验数据汇总表

4 结 束 语

基于对集装箱码头系统弹性的不确定性因素分析，结合弹性在物理学、供应链学等其他领域内的研究现状以及码头内部的实际情况，对集装箱码头系统弹性的概念进行阐述，并深入探讨其影响因素及形式化描述方法，从定性及定量两个层面对集装箱码头物流系统弹性进行研究.以某临港集装箱码头为研究案例，采用系统仿真技术，构建其概念模型及仿真模型，并设计系统弹性仿真试验，实现集装箱码头物流系统弹性的定量测度.主要研究成果如下：①通过实际案例的仿真试验证实了系统弹性形式化描述方法的科学性和可行性.②将系统弹性测量和仿真建模相结合，提出了有效的集装箱码头物流系统弹性仿真试验方法.③通过对集装箱码头物流系统弹性的形式化描述，为码头应对不确定干扰的管理水平提供有力的参考和帮助.