基于自适应转弯模型的交互式多模型算法研究*

程 遥 吕植勇

(武汉理工大学国家水运安全工程技术研究中心1) 武汉 430063) (武汉理工大学智能交通中心2) 武汉 430063)

0 引 言

对于海上高速飞行器的跟踪，如何构建与实际飞行方式相匹配的飞行器的运动模型是跟踪的关键.国内外研究学者在这个方面进行广泛的研究，对于民用航空，由于飞行器在高度上很少发生机动，水平方向上的机动可以由机动转弯模型(CT)有效的表示[1]，然而飞机的转弯速率往往是未知的，在跟踪算法中往往需要设置转弯速率，如果设置的转弯速率与实际不符合，则会出现较大的估计误差.因此，人们在CT模型的基础上进行了研究，一种方法是对每个可能的转弯率都建立相应的转弯模型，作为交互式多模型算法(IMM)的模型集[2]，另一种方法则是通过在线计算转弯率来构建自适应转弯模型[3]，但现有的自适应模型均是依据滤波器输出的估计数据来实时调整转弯率，如果滤波器输出误差较大则估计的转弯速率也与实际偏差较大，另外，使用粒子滤波算法时，由于未使用实测信息，大量的计算用在对多余粒子的计算.因此，粒子贫化是常见的现象.

本文首先对机动转弯模型进行分类和总结，在此基础上本文提出一种基于时延约束的自适应转弯模型，借助测量时延数据来构建转弯速率估计器，从而实时计算转弯率，同时由于使用实测时延数据，可以避免在不满足时延测量的粒子上花费大量计算,将修正后的转弯模型加入到交互式多模型算法中(IMM)，以实现对转弯机动目标的目标跟踪.

1 转弯模型及改进方法

转弯模型也称作协同转弯模型，其形式简单，且能较为真实的描述目标的转弯机动过程，因此在目标跟踪中被广泛使用，其在直角坐标系下的离散模型为

[A]=[B][C]+[D][E]

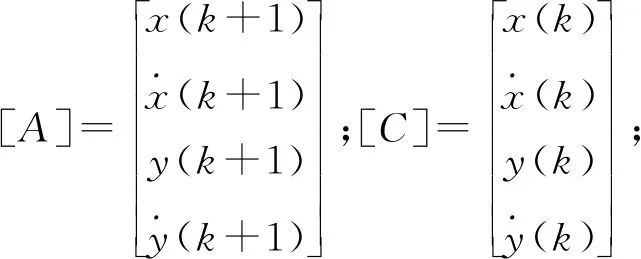
如果目标转弯速率已知，模型就可以较好的描述目标的运动轨迹，然而在实际中一般都不知道目标的转弯速率，现有的方法多是将CT模型引入到交互式多模型算法(IMM)中，不同的转弯率可以认为是不同的模型的组合.然而，尽管IMM算法能增大对目标机动的覆盖范围，但是如果模型集中的模型均不符合实际的机动，跟踪的精度将明显降低.

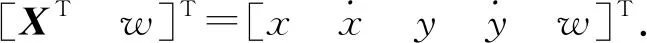
文献[5]中使用滤波器估计速度实时估计转弯率，然而由于对转弯率的估计未使用已知的数据，如果滤波器输出误差较大则估计的转弯速率误差也会增大.

2 附加估计器的转弯速率模型

在飞行器跟踪方面，由于民用飞机主要机动在水平方向，2D转弯模型是常用的跟踪模型.

文献[6]中，根据转弯模型，目标的转弯速率可以由以下公式进行估计.

(2)

(3)

式中：T为采样周期，理论上式(2)～(3)计算的转弯速率一致，然而由于使用的是估计值，误差的存在使得两者并不相等.本文在此基础上在估计器中增加测量时延/距离的约束，根据转弯模型，利用估计的位置信息估计转弯速率以减少估计的转弯速率误差.

假设传感器测量时延为τ，转换成距离为r.目标的估计运动过程由下式估计目标的位置.

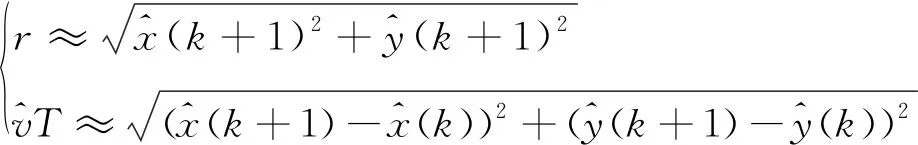
(4)

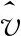
(5)

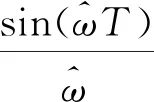
将上文模型作为交互式多模型算法(IMM)的一个模型，与其他模型交互作用，以达到更好的估计效果.其工作原理图如下：

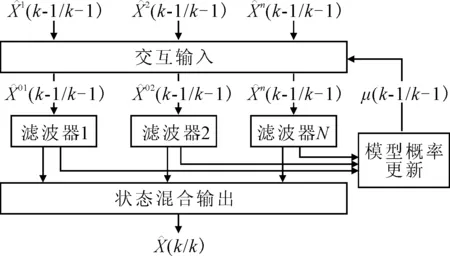
图1 交互式多模型算法工作原理

本文使用基于粒子滤波算法的交互式多模型(PFIMM)，对每个粒子均估计转弯速率，PFIMM的具体的计算过程由文献[7]给出.

3 仿真验证

仿真试验中，设置三组对照组，对照组分别使用一个匀速直线模型和两个转弯模型.实验组则使用匀速直线模型和本文所述自适应转弯模型，利用Matlab进行20次Monte-Carlo仿真，最后对比三组实验的均方误差[8-10].

假设目标在整个过程中历时500 s，初始位置为(200 m,150 m)，初始速度为(150 m/s,60 m/s)，采样间隔T设置为5 s.1～170 s，目标做匀速直线运动；171～200 s目标做转弯速率为2°/s的转弯运动，201～300 s做匀速直线运动，301～400 s做转弯率为5.1°/s的转弯运动，401～500 s做匀速直线运动.其航迹见图2.

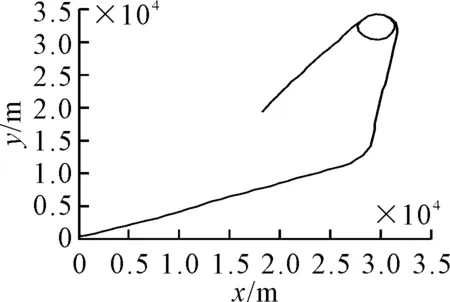
图2 目标轨迹图

本文使用3个算法进行跟踪对比，模型1设为IMM1，IMM1算法中包含三个模型，其中一个转弯模型，转弯率设置为2°/s，另一个转弯模型转弯率设为5.1°/s，以及一个匀速直线模型，模型的转移概率为

(6)

模型初始概率均设置为匀速直线模型为0.6，另外两个转弯模型均为0.2.

IMM2模型也包含三个模型，其中一个为转弯速率为1°/s的转弯模型，另一个转弯模型转弯率为7.2°/s，以及一个匀速直线模型，模型转移概率以及初始概率和IMM1相同.

IMM3则作为实验组，其中有两个模型，一个是匀速直线模型，另一个则为本文所述自适应转弯模型.模型初始概率为，匀速直线模型0.9，自适应转弯模型0.1.模型转移矩阵为

(7)

计算得到的轨迹均值见图3.

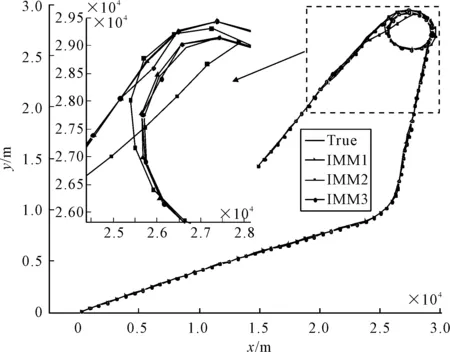
图3 滤波器输出轨迹

由图3可知，三个模型均能实现一定精度的跟踪，未出现滤波发散的现象，图4为三组模型跟踪的误差值.

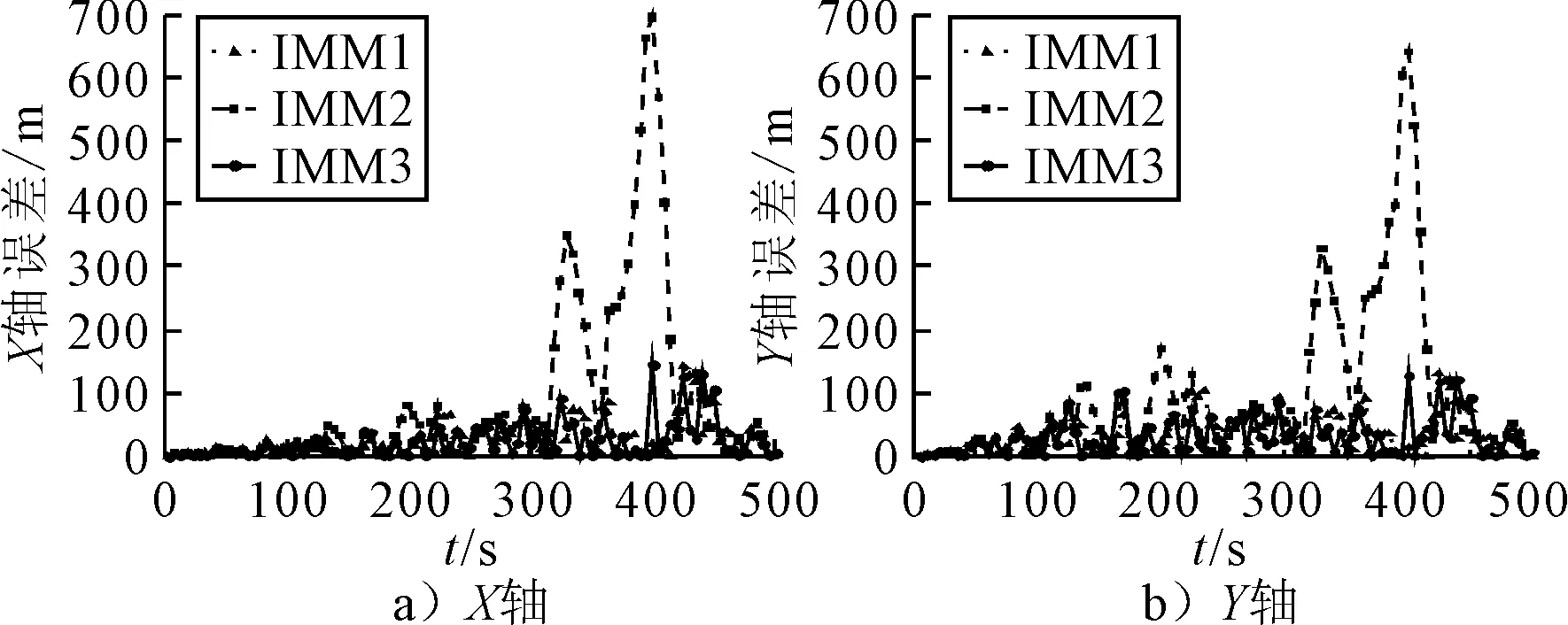
图4 各个模型坐标均方误差

由图4可知，IMM1由于转弯模型的转弯速率与实际转弯速率相同，因此其跟踪误差相对较小且比较平稳，而IMM2在第一次转弯时刻以及匀速直线运动时刻误差均与IMM1相近，这是由于IMM2中第一次转弯率设为1°/s，与实际2°/s的转弯率相差较小，而在300～400 s期间，由于模型中转弯率均与目标实际转弯率相差较大，因此误差明显高于IMM1.IMM3则在整个过程中表现出与IMM1相近的跟踪精度，由于IMM3中未设置固定的转弯率，可见，其估计的转弯率与实际转弯率相近.

4 结 束 语

本文提出一种基于时延约束的自适应转弯速率模型，在现有的基于速度估计转弯速率的模型基础上，增加了测量时延作为估计约束，提高估计的精准度，在仿真试验中，比较了几种基于预设模型集的交互式多模型算法的跟踪效果，仿真结果表明，该方法能有效的估计目标的转弯速率，具有一定的适应性，相比于模型集中转弯速率与实际转弯速率不同的情况，跟踪精度实现了有效提高.