多自由度高静低动刚度隔振系统的反馈控制研究*

刘树勇 苏 攀 位秀雷 刁爱民

(海军工程大学动力工程学院1) 武汉 430033) (中国人民解放军91404部队2) 秦皇岛 066000)

0 引 言

如何有效的进行低频隔振一直以来是振动领域的热点问题.为了提高隔振器的隔振范围，可减小隔振器的固有频率，这将意味着降低系统刚度，从而使得系统的承载能力下降.为了克服这一缺点，诸多学者提出了具有高静低动刚度性能的隔振器.高静低动刚度隔振器由正刚度机构和负刚度机构并联组成，其中正刚度机构用于承受主要载荷，负刚度机构用于抵消正刚度弹性元件的刚度，使得系统在静态平衡位置处的刚度趋于零.Ivana等[1-6]将倾斜弹簧作为负刚度机构与垂直弹簧并联组成高静低动刚度隔振器，并详细研究了其幅频特性及传递特性.Xu等[7-9]使用电磁弹簧作为负刚度机构，设计了准零刚度隔振器，并进行了理论与实验分析.Meng等[10]提出来一种具有等厚和变厚度蝶形弹簧准零刚度隔振器的设计，并利用平均法研究了系统参数对隔振器传递率的影响.Huang等[11]利用欧拉屈曲梁作为负刚度机构，分析了该高静低动刚度隔振器的静力与动力学特性并进行了试验研究，验证了高静低动刚度隔振器比线性隔振器具有更宽的隔振频带.

目前对含反馈的多自由度高静低动刚度隔振系统动力学特征的控制规律研究较为鲜见.本文应用平均法研究反馈控制对高静低动刚度振动系统动力学特性的影响，得到系统响应幅值和控制参数之间的关系式，并对系统在Van der Pol平面上的解进行分析.

1 高静低动刚度系统力学特性分析

高静低动刚度系统原理见图1.两个负刚度倾斜弹簧与一个正刚度垂直弹簧在O点连接，正刚度弹簧元件刚度为kv，两负刚度弹簧元件的长度相同，且另一端安装点的高度相同，安装点距离系统中心点的距离为a，左侧弹簧刚度为kl，右侧弹簧刚度为kr，系统处于静平衡位置时，正刚度弹簧元件的压缩量为h0.

坐标x定义为点O从初始位置开始在竖直方向上的位移，向下为正，则系统的力与位移的关系为

(1)

进行无量纲化，可得：

(2)

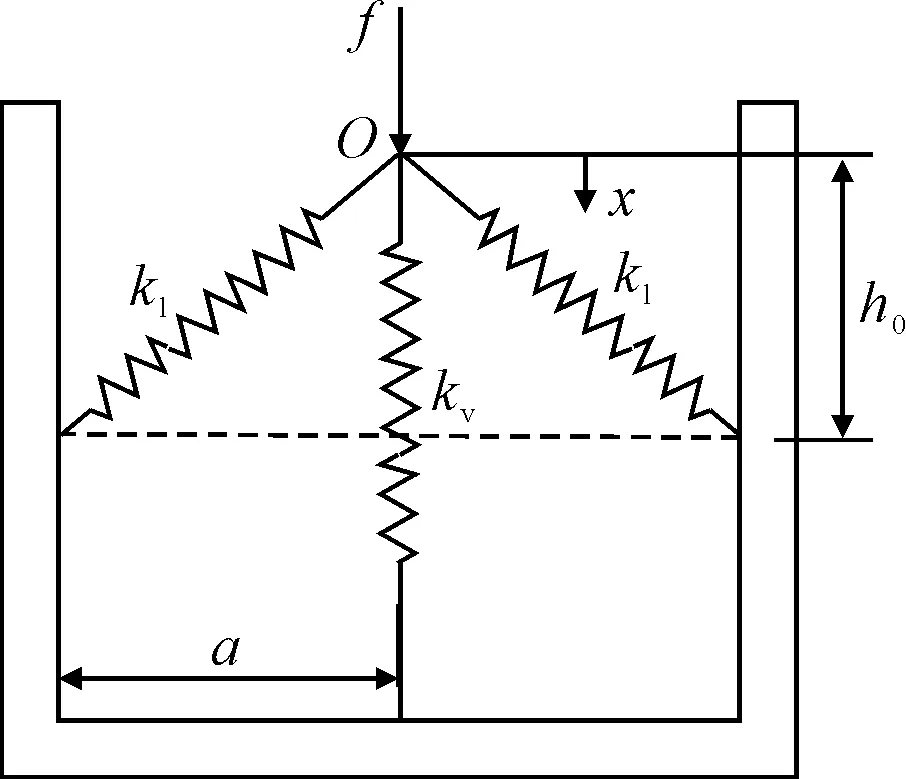
图1 高静低动系统原理图

根据刚度定义，将式(2)对位移求导得准零系统的无量纲刚度为

(3)

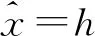
(4)

当α=1时，无量纲力-位移及刚度-位移曲线见图2.由图2可知，当h=hQZS时，系统在静平衡位置时由两侧弹簧产生的负刚度与垂直弹簧产生的正刚度相互抵消，可获得准零刚度特性；当hhQZS时，系统在静平衡位置时刚度为负值.

图2 量纲一的量力-位移和刚度-位移曲线图

(5)

则刚度为

(6)

图3 力和刚度的近似表达式与精确表达式对比曲线(α=1,h=hQZS)

高静低动刚度隔振器无量纲力及刚度精确表达式与近似表达式对比曲线见图3.由图3可知，无量纲力及刚度近似表达式与精确表达式的误差随着位移量的增大而增大.当系统在平衡位置附近处位移量较小时，近似表达式与精确表达式的误差很小，三阶泰勒级数展开式能很好地模拟精确表达式.

2 高静低动刚度系统反馈控制模型

两自由度高静低动刚度振动系统反馈控制模型见图4，其中系统的激振力幅值为F，频率为Ω；上层质量块为M1，振动位移为X1，阻尼系数为C1； 下层质量块为M2，振动位移为X2，下层弹簧元件刚度为K2，阻尼系数为C2.反馈控制回路中，传感器采集上层质量块速度信号，作动器安装于上下质量块之间，根据反馈信号控制上层质量块的振动，因此作动器的力可表示为：P=K1Z1.

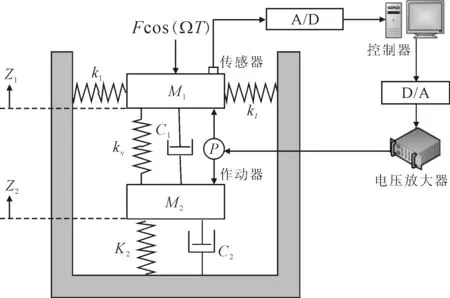
图4 两自由度高静低动刚度系统反馈控制模型

系统的微分方程为

Fcos(ΩT)+M1g-P

(7)

系统的量纲一的量运动微分方程为

fcos(ωt)-kz1

(8)

3 平均法分析系统响应

对式(8)而言，其精确解难以得到，为便于研究，采用平均法研究方程的近似解以及反馈增益对解的影响.

假设在线性条件下，式(8)基本解为

(9)

对式(9)求导，可得

(10)

在非线性条件下，由于振动的复杂性，假设可以得到与式(9)在形式上相同，但系数具有时变特征的基本解，其表达式为

(11)

同时假设系统的振动速度具有式(10)相同的形式：

(12)

由于方程(10)求导后可得到

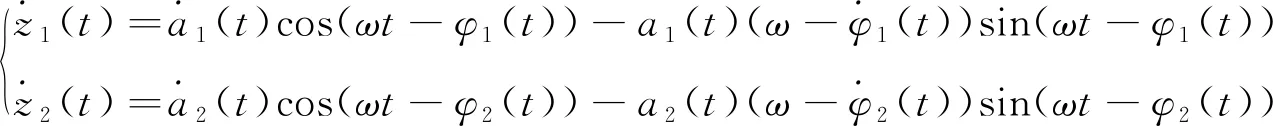
(13)

联立式(12)～(13)，得到

(14)

对式(12)求导，得到二阶导数形式

(15)

将式(12)～(14)代入式(2)中，可得

(1+k-ω2)a1(t)cos(ωt-φ1(t))-ωξ1a1(t)sin(ωt-φ1(t))-fcos(ωt)+

(16)

χ+(v1+μ-ω2)a2(t)cos(ωt-φ2(t))-(ωξ2+μωξ1)a2(t)sin(ωt-φ2(t))+

3rμ(a1(t)cos(ωt-φ1(t))-a2(t)cos(ωt-φ2(t)))a2(t)a1(t)cos(ωt-φ1(t))cos(ωt-φ2(t))+

(17)

利用式(14)、式(15)和式(17)直接求出式(9)中幅值和相位参数的一阶导数解析表达式.

(18a)

(18b)

(-(v1+μ-ω2)cos(ωt-φ2(t))+(μξ1+ξ2)ωsin(ωt-φ2(t)))a2(t)-

(18c)

(-(v1+μ-ω2)cos(ωt-φ2(t))+(μξ1+ξ2)ωsin(ωt-φ2(t)))a2(t)-

(18d)

为方便进行分析，将非自治系统转换为自治系统，进行如下变换：

φ1(t)=ωt-θ1(t)，φ2(t)=ωt-θ2(t)，ωt=θ1(t)+φ1(t)

则变换后，式18a)～d)变为

(19a)

(19b)

(19c)

(19d)

假设参数a1(t)，a2(t)，φ1(t)，φ2(t)具有慢变特性，对式19a)～d)等式右边在一个周期T( 0～2π) 范围内积分，并计算该区间的平均值，可得：

(20a)

[πfcosφ1(t)/ωa1(t)]-

(20b)

(20c)

(20d)

由式20b)可得，反馈参数k的存在对相位产生了影响，同时由于20b)中含有a1(t)和a2(t)，它们和式20a)和式20c)是非线性耦合的，因此还造成响应幅值的改变.由于相位变化与控制过程中延迟有重要关联，因此，这一结果表明多自由度高静低动刚度振动控制中增益对延迟具有影响.在施加控制的过程中，相位的补偿不仅需要考虑系统本身的延迟，而且考虑控制增益参数的影响.此外，如果响应的幅值ai(t)i=1，2在t趋向于无穷大为常数时，则系统的解曲线收敛于一个极限环，而当ai(t)i=1,2不为常数时，则系统的解将非常复杂，可能出现拟周期甚至混沌状态.

4 系统动态特性分析

当系统无反馈时，式(8)中参数的取值为ξ1=0.2、ξ2=0.2、μ=1、f=10、ω=3、r=1、v1=1、χ=2.通过式20a)～d)可预测系统的长期行为，见图5a).此时系统振动幅值a1(t)随时间无限增大，趋向于常数3.758.说明系统处于周期运动，系统的运动最终将收敛到极限环上.当对系统进行反馈控制时，反馈增益取为k=5，其余参数不变，结果见图5b).此时系统振动幅值a1(t)随时间增大，趋向于常数2.926.表明系统的运动仍处于周期运动.对比可发现：通过反馈控制后，极限环变小.为了观察二维平面上的收敛行为，给出了Van der pol 平面上的收敛轨线，见图5c～d).因此，通过对解析表达式的计算分析可以了解非线性系统的长期特性，以及反馈控制后的响应趋向.显然，通过反馈控制后，能够降低振动幅值.

图5 应用近似解析方法得到响应的特征

当反馈增益进一步增大为k=10，其余参数保持不变，见图6.由图 6可知，此时响应的幅值收敛到1.996 ，即随着控制强度的增加极限环大小进一步降低，振动得到进一步抑制.

图6 反馈增益增大时的响应幅值收敛行为

改变系统的参数，如阻尼减少，激励频率增大，观察结果的变化.当参数的取值为ξ1=0.05，ξ2=0.01，μ=1，f=10，ω=3.8，r=1，v1=1，χ=2时进行计算，见图7.系统振动幅值a1(t)，a2(t)随时间增大始终在一定范围内波动，表明在不同初始条件下，系统的解并不是在单一的极限环上，而是在“极限环带”上运动，此时系统可能处于多周期运动或混沌运动.

图7 系统响应形成的极限环带

为了说明图7的预测结果，改变反馈控制增益大小，得到系统Lyapunov指数谱曲线随反馈增益变化的规律，见图8. 由图8可知，反馈增益在0.02～2范围呈现混沌运动，最大Lyapunov指数大于零；在2～10范围内，混沌运动和周期运动区域相互交错.该结果与图7理论预测结果相吻合.

图8 随反馈增益变化的Lyapunov指数谱

5 结 束 语

本文建立了含反馈控制的多自由度高静低动刚度隔振系统的数学模型，应用平均法推导了多自由度高静低动刚度隔振系统的响应幅值随反馈增益变化的解析表达式，并预测了系统响应的久期变化趋势，得到了Van der Pol二平面上的极限环.当存在“纯净的”极限环时，系统的呈现简单的周期振动；当极限环转化为“环带”时，系统的运动变得复杂，存在拟周期和混沌运动状态.多自由度高静低动刚度系统中引入反馈控制后，既可以将系统的混沌响应控制到周期状态，抑制其有害的混沌振动；也可以通过反控制进入小幅值混沌状态.