“预报挑战度”和“可预报性演变指数”简介

■ 杜钧 邓国

（作者单位：杜钧，美国国家海洋和大气管理局国家环境预报中心；邓国，中国气象局数值预报中心）

“预报挑战度”（measure of forecast challenge，MFC）是一种衡量预报难易的新尺度；“可预报性演变指数”（predictability horizon diagram index，PHDX）是一种检验集合预报的新评分。这二种新指标是杜钧等于2019年提出来的，文章发表在美国气象学会英文杂志《天气和预报》上。为了让国内基层台站业务预报和研发人员也能熟悉和应用这些方法，我们在此作一简短的总结介绍。

1 方法提出的动机和目的

目前我们都是用预报的误差大小来度量一个数值预报的好坏。引入集合预报后，预报的可信度可以用集合离散度来定量化。对预报员和用户而言，同样一个预报，虽然它们的集合平均预报误差可能一样，但不确定性大（可信度低）的预报显然比不确定性小（可信度大）的预报更难在具体决策中运用（图1）。“预报挑战度”就是既考虑预报误差又考虑预报可信度，来综合衡量预报的质量。这相当于把一张二维的平面照片变成了一张三维的立体图形，希望能更准确地描述一个物件。

图1 集合预报1和2（黑色为成员，红色为集合平均）。虽然它们的集合平均预报很相似，但集合离散度相差很大。显然，集合预报2在预报员或用户决策过程中比集合预报1更难应用

针对某一地点某一天气（如北京某一日08时的风向），通常预报检验都是针对某一个给定的预报（如前一日08时发布的预报）在某一预报时刻（如24小时预报）进行的，而不考虑过去曾对该天气事件发布过的所有预报的时间演变情况。而现实中，过去预报结果的时间演变对预报员或用户决策过程难易程度和成败起了重要作用：有些起了积极作用、有些起了误导作用。现有的集合预报检验方法并没有把这个时间演变情况考虑在内，而新提出的“可预报性演变指数”把过去一系列预报的时间演变特征定量地考虑进去了，如预报的稳定情况（误差变化）和可信度的变化（离散度变化）。这样在检验指标中加入时间维度后，相当于把照片变成了录像，希望能更全面地反映真相。

2 方法介绍

2.1 预报挑战度（MFC）

任何一个变量在给定的某一地点和预报时刻，它的“预报挑战度”可以通过公式（1）从一个集合预报中计算出来：

式中包括了4个同预报难易程度有关的要素（集合平均预报误差EME、离散度Sprd、非线性度量NonLN和实况出界程度OUT），它们分别通过式（2）～式（5）来定义。EME、Sprd和NonLN 量级差不多，所以没有进行正态化处理；出界度是对前三项之和的修正，如果实况出界就增加惩罚。分析表明这4个元素除享有共同的信息外，还在很大程度上提供相对独立的信息。

EME 是集合平均预报m同观测O之差的绝对值，反映的是一个模式的平均预报水平：集合离散度Sprd定义为n个成员预报mi相对集合平均m的标准差：

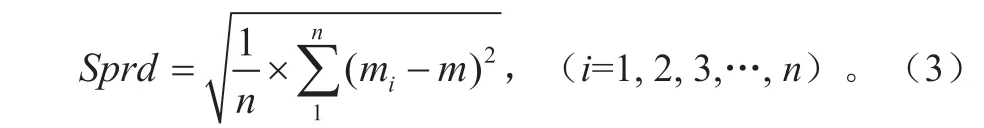
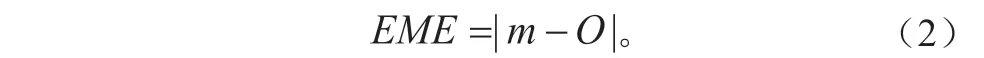
非线性度量NonLN 应用Du和Zhou（2011）的定义，为控制预报mctl同集合平均预报m之绝对差值：

Sprd和NonLN都同大气可预报性和集合扰动技术有关。出界度OUT描述实况O是否被集合解所包含，如果被包含就是0.0（式5c）， 否则就定义为出界程度，即超出集合边界的距离相对于集合解宽度（最大解mmax和最小解mmin之差 ）的比率（式5a 和5b）：

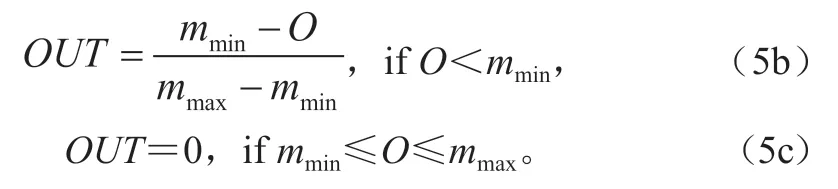
所以，MFC不但包括了模式预报误差，还考虑了预报的不确定性，大气运动的非线性程度，以及实况是否被集合预报解所包括（同集合预报系统的设计和模式系统性偏差有关）。分析表明，此指标中集合平均预报误差贡献最大，其次是离散度，然后是非线性度量，出界率贡献最小。譬如，用NCEP 全球集合预报中高度、温度、湿度和风场的126小时预报资料计算的平均结果看到，EME、Sprd、NonLN 和OUT 与MFC 的空间相关系数分别为0.85，0.7，0.6和0.3。

2.2 可预报性演变指数（PHDX）

对于某一天气事件，随着预报时效愈来愈接近，集合预报解随时间的演变可以有如下4种情形（图2）：1）符合实况的成员数不断增多而不确定性减小（图2A中a）；2）同上相反，尽管离散度也变小，但符合实况的成员数反而变少（图2B中a）；3）集合解不随时间收敛（不确定性保持很大），但包含了实况（图2C中a）；4）离散度保持很大，且实况基本不被包含（图2D中a）。如果用MFC来衡量的话，在第一种情形中MFC随着事件的接近而变小，该预报为用户决策提供了可靠有用的信息，称为第一类（Type Ⅰ，图2A中c）；第二种情形下，MFC 变大，误导了用户的决策过程，称为第二类（Type Ⅱ，图2B中c）；在第三和四情形中，MFC随预报时长变化不大，但前者MFC值稍小（因为实况包含其中），后者值稍大（因为实况不在集合解中），该类预报由于不确定性不减小，很难帮助用户决策，称为第三类（Type Ⅲ，图2C中c和图2D中c）。

为了定量反映上述4种可能的情形，“可预报性演变指数”定义如下：

式中Trend 是过去一系列集合预报的 MFC 值随天气事件逼近时（图2中的t = 12, 11, …, 2, 1）的时间变化净趋势：

式中，t=T 代表最远的预报，t=1代表最近的预报，Avslp是MFC在所有众多二个相邻集合预报间变化的平均值（平均斜率）：

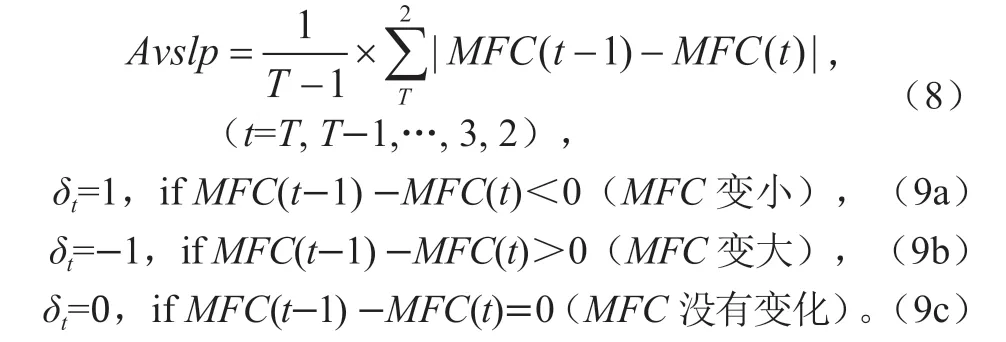
Mag是所有预报的MFC值之总和：

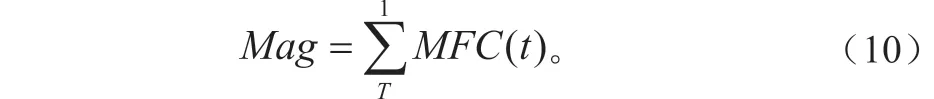
图2 （A）“第一类”情形：（a）集合预报随时间的演变（水平实线表示实况obs，虚线表示集合平均，红点表示集合成员），“第一类”情形下有三个阶段，先是个别成员接近实况，然后更多的成员围绕着实况，最后是离散度变小、集合解向实况收敛；（b）计算MFC中四要素；（c） MFC 的时间演变。（B）“第二类”情形。（C）和（D）“第三类”情形：前者集合解包含了实况，后者漏了实况

PHDX值的变化范围为-1.0～1.0，正值对应“第一类”情形，负值对应“第二类”情形，零值附近对应于“第三类”情形。对应图2中的4种情况，它们的PHDX值分別为0.30（图2A），-0.11（图2B），0.00（图2C）和-0.01（图2D）。

PHDX可以用来比较不同集合预报系统的预报能力，或对于同一个集合预报系统来区分哪些天气事件或要素可预报性较高或较低等。譬如,图3是用NCEP区域集合预报SREF的实际降水和温度预报资料计算的例子：图3a～3c分别是集合降水预报可预报性演变的“第一类”“第二类”和“第三类”情形；图3d是离地表2 m高度处的气温集合预报可预报性演变的例子（“第一类”）。经过许多例子的检验，发现气温预报出现“第一类”的情况远多于降水，或说气温的可预报性一般大于降水，这同我们的实际经验是相符的。原文中还对NCEP全球集合预报系统GEFS预报的二次大雪过程进行了计算，也表明PHDX 有能力来区分同一天气过程但不同地点其可预报性的高低。

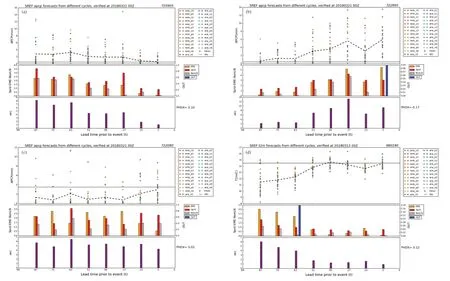
图3 同图2，但是用NCEP区域集合预报SREF的实际降水和温度预报资料计算的例子：（a），（b）和 （c）分别是集合降水预报可预报性演变的“第一类”（PHDX=0.10）、“第二类”（PHDX=-0.17）和“第三类”（PHDX=0.02）情形；（d）是离地表2 m高度处的气温集合预报可预报性演变的例子（“第一类”，PHDX=0.12）

3 结论

随着集合预报的出现，预报可信度成了衡量一个预报信息的重要度量，所以检验预报的评分指标也应该包括这一应用价值的度量，“预报挑战度”就是为了适应这一需要而提出来的，它除了预报误差还考虑了预报不确定性。对某一天气事件，其预报信息的时间演变对预报员或用户作决策有重大的影响，一个稳定而又准确的预报是用户所期待的，而一个不准确或多变或不确定性很大的预报对用户决策会起误导作用或无法决策。所以，预报评价指标中应该考虑预报的时间演变，本文中的“可预报性演变指数”正是这一方面的新尝试。由上可知，此二种预报评价新指标的出发点是以预报员或用户决策过程的难易程度和准确性为标准，而并不以直接描述被预报的天气过程难易程度或揭示预报模式的某些缺陷为目标，虽然它们会有某种程度上的联系。

因为此二种指标刚提出不久，实际例子应用还不多，所以希望大家多应用，并在应用中逐步改进完善它们。

深入阅读

杜钧, 2002. 集合预报的现状和前景. 应用气象学报, 13(1): 16-28.

杜钧, 周斌斌, 2016. 雾的集合预报与集合预报的检验. 气象科技进展, 6(3): 41-47.

Du J, Zhou B, 2011. A dynamical performance-ranking method for predicting individual ensemble member performance and its application to ensemble averaging. Monthly Weather Review, 139: 3284-3303, https://doi.org/10.1175/MWR-D-10-05007.1.

Du J, Zhou B, Levit J, 2019. Measure of forecast challenge and predictability horizon diagram index. Weather and Forecasting, 34: 603-615.

Greybush S, Saslo S, Grumm R, 2017. Assessing the ensemble predictability of precipitation forecasts for the January 2015 and 2016 east coast winter storms. Weather and Forecasting, 32: 1057-1078. doi: 10.1175/WAF-D-16-0153.1.