基于CUSUM算法的LDoS攻击检测方法
2020-06-03盛钟松
苟 峰, 余 谅, 盛钟松
(四川大学计算机学院, 成都 610065)
1 引 言
拒绝服务(Denial-of-Service, DoS)攻击利用TCP三次握手的缺陷来消耗网络、服务器集群或终端主机的资源,从而严重降低或拒绝对合法用户的服务.DoS攻击的典型特征是实施攻击过程中涉及大量机器,具有极高的数据率,其明显的统计异常极易被入侵检测系统(Intrusion Detection System, IDS)检测到,并降低攻击造成的影响.2001年,美国AstaNetworks在Internet2Abilene骨干网络上检测到一种新的DoS攻击手段,与DoS、DDoS攻击不同,该攻击平均速率很低,难以被已有的DoS检测手段发现.这种低速率DoS(Low-rate DoS,LDoS)攻击被Kuzmanovic等人称为“地鼠攻击”(ShrewAttacks)[1],后来也有研究者称之为降质攻击(RoQ,Reduction-of-Quality)[2-3]、脉冲式拒绝服务攻击(Pulsing DoS Attacks)[4]等.LDoS攻击是利用TCP的超时重传机制的漏洞,攻击者通过恶意选择攻击周期、攻击强度和攻击持续时间来使TCP接收窗口维持较小值甚至近零.
简单LDoS攻击的模型如图1所示.该模型可用三元组(T,τ,δ)来表示,其中,T为攻击周期,表示连续两次攻击之间的间隔,文献[1]中建议的攻击周期为1 s.但已有研究者表明攻击周期T选择可以由攻击者通过链路状态进行预估[3];τ为攻击持续时间,表示周期内攻击持续的时间长度;δ为攻击强度,表示LDoS攻击流的速率.
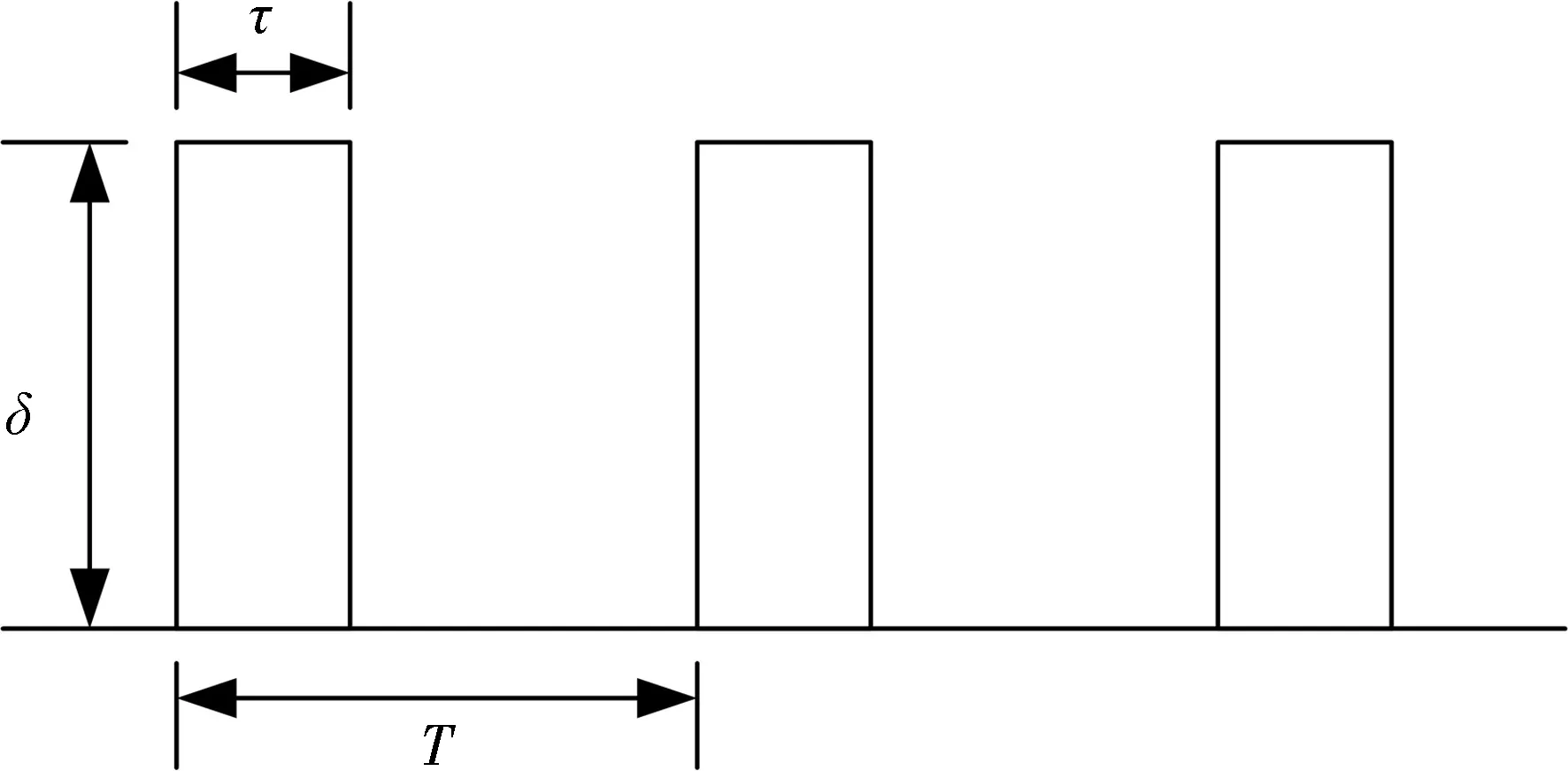
图1 LDoS攻击模型Fig.1 The model of LDoS Attacks
自LDoS提出以来,国内外许多研究机构对此进行了研究.对LDoS的检测普遍是利用数字信号处理的方法,提取网络流量的频域特征进行检测[5],其中典型的有基于小波变换[6-7]、基于协同检测的检测方法.虽然从频域的角度能实现不错的检测效果,但这种方式需要准确的提取特征,并进行复杂的运算,这导致检测过程时延较大,实时性达不到要求.此外,在当前网络大数据的情况下,该方法也有一定的局限性.因此,结合机器学习的检测方法成为新的选择,但是应用此方法缺少有效的数据集,主要是通过仿真工具产生实验数据,规模性与多样性不足.从时域的角度对网络层的链路状态特征分析[8-10]实现LDoS的检测是目前一种新的思路,本文的方法也是基于这一角度出发,对路由器的入口流量进行分析,利用基于累计和(Cumulative Sum,CUSUM)算法累积异常,累积值超过阈值即触发报警,实现异常检测.目前,针对低速率拒绝服务攻击的研究已经从这种攻击方式的仿真实现[5,11-12]进入到检测和预防[13],应用领域逐渐深入到域间路由系统[14-15]与数据中心[16].
2 相关工作
目前已有许多研究者提出了不同的检测方法.Bhuyan等[17]提出一种利用广义总变差的方法来检测多维度的LDDoS攻击,该方法利用抖动窗口计算每个时间周期内的广义总变差,从而定位异常.吴志军等[18]通过研究网络中正常情况和存在LDoS攻击时ACK序号步长的波动差异,利用排列熵算法实现了对LDoS攻击的检测.Zhang等[19]提出利用核心主成分算法对队列特征进行降维,再结合机器学习算法根据网络状态来检测LDoS攻击.Hayashi等[20]证明突发攻击流量的持续时间是从正常流量中区别LDoS流量的较好特征,提出利用路由器快速分组匹配功能来检测LDoS攻击.Xiang等[21]提出了利用广义熵和信息距离为度量,量化不同概率分布的差异,通过计算广义熵和信息距离来检测LDoS攻击流量.Rashed等人[22]提出了利用优化的Sigmoid滤波器来检测LDoS攻击的方法,在允许通过指定带宽的路由器上设置带宽阈值,超过该阈值的流量则丢弃,或者重定向到蜜罐服务器.何炎祥等[23]提出了一种基于小波特征提取的LDoS检测方法,通过小波多尺度分析,提取LDoS攻击规律的特征,采用BP神经网络来训练检测模型.Chen等[24]提出了协同检测过滤的方法检测LDDoS攻击的方法,该方法利用离散傅里叶变换DFT对采样时间内的自相关序列进行频域转换,利用能量谱密度PSD来区分合法流量与LDoS攻击流量.Chen等[25]提出了一个使用(Field Programmable Gate Array,FPGA)进行能量谱密度分析的嵌入式加速器,它利用强大的计算能力和与软件相似的灵活性.该方法能在复杂背景流量中提供高质量的恶意流量检测,但是需要较高的硬件成本.
虽然LDoS攻击具有很强的隐蔽性,但是其攻击仍然会造成正常流量的统计异常.本文在对LDoS攻击原理及特征分析的基础上,结合CUSUM算法对统计异常进行累积,一旦累积值超过设定的阈值即可触发异常警报.
3 基于CUSUM算法的LDoS检测
3.1 CUSUM介绍
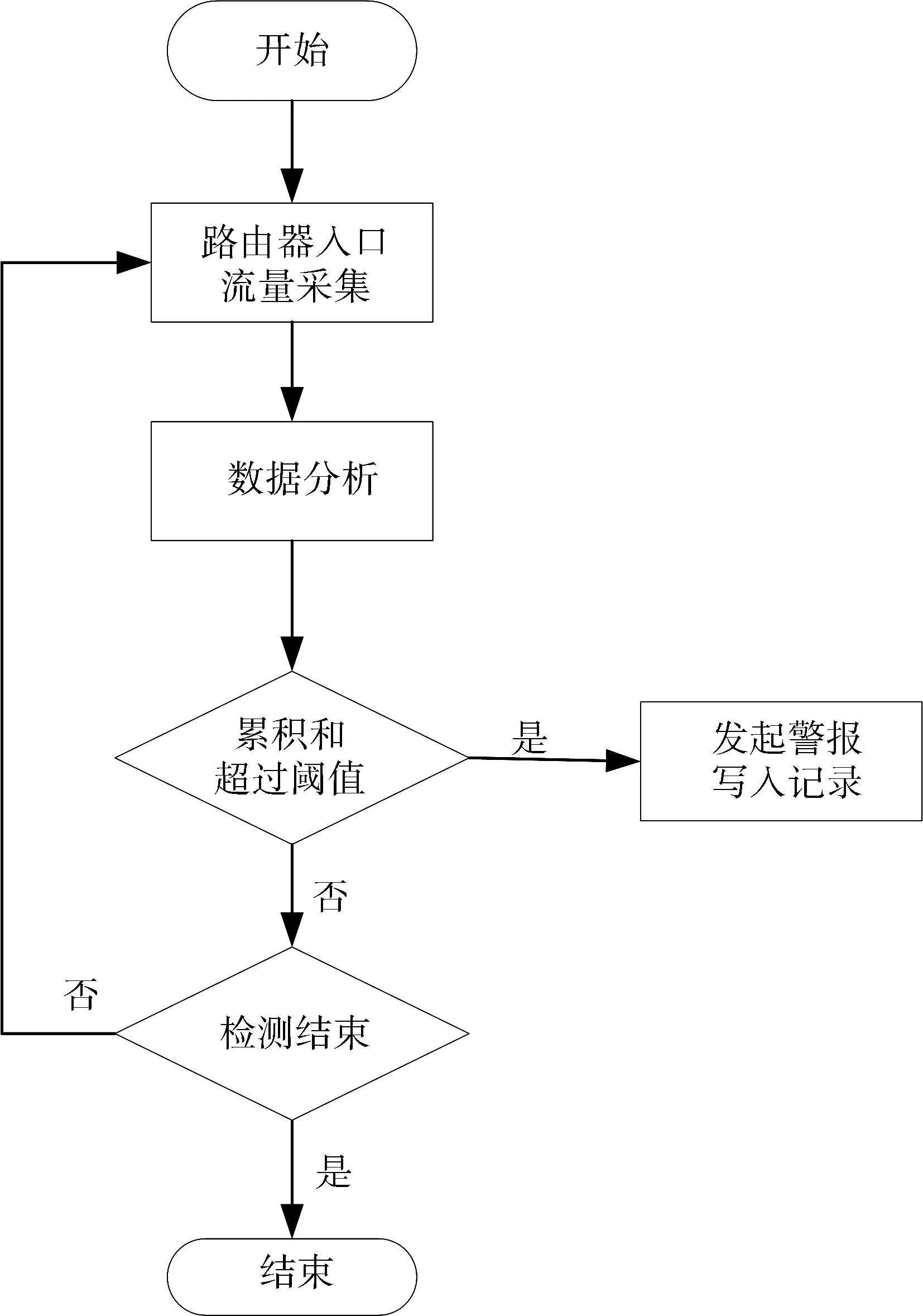
CUSUM算法[26-28]属于基于假设检验的变点检测算法族,针对独立同分布的随机变量设计,对过程均值有无漂移进行检验.令y1,y2,…,yθ为独立同分布N(0,1)变量,而yθ+1,yθ+2,yθ+3,…为独立同分布N(δ,1)变量,其中变点θ未知,对给定观察序列y1,y2,…,yn,备选假设θ=ν(ν (1) (2) 若已知δ>0,则上述似然比统计量等价于下述统计量,如下式. (3) 在正常情况下,Zn<0,对于给定门限值h,如果Zi (4) 计算可得Zn的递推公式 (5) 由于因特网是一个复杂的动态实体,因此采用非参数的CUSUM算法更利于分析,非参数CUSUM算法的核心思想是累积明显高于正常情况下平均水平的Yn值.该算法的优点之一是能持续监控输入的随机变量,达到实时检测的效果. 对路由器入口流量观察序列{yn},yi为第i时刻到达的流量大小(以字节为单位),μi为第i时刻到达的平均流量大小,μn由指数加权移动平均EWMA(Exponentially Weighted Moving Average)的方式得出,具体表达式如(6)式所示. μn=β1yn+(1-β1)μn-1,μ0=y0 (6) 其中,β1为EWMA因子. dn=max{0,dn-1+yn-(μn+K)},d0=0 (7) 通常情况下,K是保证E(dn-1+yn-(μn+K))在正常情况下小于0的值,即dn=0. 由于网络中流量模式是动态变化的,在应用CUSUM算法检测LDoS攻击时,如果固定异常计数器dn的阈值将会限制检测性能与应用范围,因此该阈值为动态确定的,如(8)式所示. (8) 其中,β2为EWMA因子;σn为yn的标准差;H为判决门限;h为决策因子,h的取值对CUSUM检测算法的性能有较大影响,如果h取值太小,那么检测表现过于激进,将会导致较高的误报,如果h取值太大,那么检测表现过于保守,将会导致较高的漏报.当dn>H时,说明检测到异常. 上述算法涉及的参数取值参考范围如表1所示. 表1 参数取值范围 根据上述内容,应用CUSUM算法实现LDoS检测的步骤如下. (1) 对路由器入口流量进行采样; (2) 将采样数据根据式(6)和式(7)式计算出采样时刻的平均流量大小μn与异常累积计数器dn; (3) 根据(8)式,结合步骤(2)分析得到的数据判断dn>H是否成立,若是,则检测系统发起警报,并将异常写入日志;若否,则转入步骤(4); (4) 判断检测是否结束,若是,则转入步骤(5);若否,则转入步骤(1); (5) 结束检测. 在检测系统运行前,需要在仿真环境中瓶颈链路速率稳定时再进行攻击.根据TCP拥塞管理机制,初始阶段发送方的发送速率是逐渐增大的过程,而本文提出的CUSUM检测算法本身是基于网络流量异常累积的,因此在仿真过程开始阶段进行检测具有较高的误报率.虽然在实验中有设定的条件限制,但是在实际环境中网络状态是处于稳定的,所以并不影响该检测算法的实际应用.检测实现过程的流程如图2所示. 图2 检测流程图Fig.2 The detection flow chart 已有研究表明,正常网络中有80%的流量为TCP[29].因此本文以TCP流量代表正常流量,以UDP流量代表LDoS攻击流量.本文实验测试环境参考美国莱斯大学Kuzmanovic教授实验团队基于NS-2的网络拓扑环境[1,11],攻击流量采用ShrewAttack攻击工具生成,实验拓扑如图3所示. 图3 实验拓扑结构Fig.3 The topology of experiment 图3中,TCP流量的产生服从指数分布,TCP窗口大小设置为128 byte,TCP报文大小为1 040 byte,UPD攻击报文为40 byte.根据图3所示的拓扑结构,其中关键参数设置表2所示. 表2 拓扑结构关键参数 本文定义性能检测指标为检测率、漏警率、误警率,具体如下. 图2中,设定节点数N=5,实验时长60 s,攻击流量在第30 s开始,此时链路状态趋于稳定,第50 s结束,实验总次数120次.图4显示了链路速率和攻击模式,图4(a)为正常情况下的链路速率,图4(b)为遭受LDoS攻击后的链路速率,图4(c)为相应的LDoS攻击流量.由图4可知,在正常情况下,链路速率趋于平稳,带宽利用率为90%左右,受LDoS攻击1.4 s之后速率开始下降,攻击停止2.5 s后开始恢复,在攻击期间链路速率下降25%左右. 图4 链路速率和攻击Fig.4 The rate of links and attack 由式(7)和式(8)知参数h和K是影响检测性能的主要因素,实验中分别设置了不同的h、K值进行比较,并取EMWA因子β1=0.8,β2=0.95.图5显示了不同h、K的取值时检测率TP和误警率FP的情况,当K值小于5、h值小于0.07时检测误警率FP偏高,图5表明当h=0.1,K=8时检测性能最好,此时检测率为96%,误警率为8%.在实验中,继续增大K时,误警率会降低,但是检测率也会大幅度下降. 图5 不同的h和K值对检测性能的影响Fig.5 The impact of different value of h and K on detection performance 图6显示了应用CUSUM算法进行检测时累积值dn及门限值H的变化图.由图6(a)可知,在LDoS攻击期间累积值dn明显偏高.注意到在0至5 s内累积值dn也明显高于门限值H,这主要是在此期间,进入路由链路的流量还逐渐增加至链路带宽引起,同时这也是误警率较高的主要原因,因此本文实验选择在路由带宽利用率稳定时进行攻击,以此来验证攻击性能与检测性能.由图6(b)可知,该检测方法的平均检测时延约2.6 s,在可接受范围内. 图6 应用CUSUM算法后的检测结果Fig.6 The detection result of applying CUSUM algorithm 本文方法与该领域已有相关检测方法性能比较如表3所示. 表3 不同算法的检测结果 从表3可知,本文方法比归一化功率密度谱NCPSD方法的检测性能更优.虽然误警率比基于网络流量奇异性特征的检测方法偏高,但是本文方法的检测率更高,总体性能更优.相对于FIR滤波器检测方法,本文方法具有更低的误警率.本文方法虽在性能上略差于基于ACK步长的检测方法,但是本文方法的计算复杂度更低.所以,本文提出的方法虽然在检测早期存在一定的误报率,但是对LDoS攻击的检测性能较为理想,总体计算复杂度更低. 本文针对路由器遭受LDoS攻击时进入链路队列的流量特征进行了时域上的分析,提出了一种基于累积和CUSUM算法的LDoS检测方法.该方法基于假设检验,分析了不同的参数取值对检测性能的影响,将累积值与链路状态突变前后的阈值相比较,从而实现LDoS攻击检测的目的.该方法占用系统资源少,易于嵌入部署到路由器上进行LDoS攻击的实时检测.本文方法与其他已提出方法相比检测率较高,有较好的检测性能.但该方法也有不足之处,在流量发生的初期会产生误报,检测到攻击之后没有对应的对抗策略来缓解攻击造成的影响,这也是后续研究的重点内容.

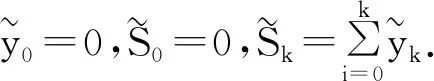
3.2 CUSUM算法在LDoS检测中的应用
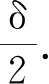

3.3 实验环境及参数的设置





3.4 实验结果分析




4 结 论
