无动力运载器倾斜爬升式上浮特性分析

张海洋，谷海涛，林扬，孙原，高浩，冯萌萌

1 中国科学院沈阳自动化研究所 机器人学国家重点实验室，辽宁 沈阳 110016

2 中国科学院 机器人与智能制造创新研究院，辽宁 沈阳 110169

3 东北大学 机械工程与自动化学院，辽宁 沈阳 110819

0 引 言

无动力运载器是一种特殊的无人水下航行器，由于具有将水下环境与内部有效载荷隔离的作用，其被广泛应用于潜射导弹、海底矿产开采等领域。部分有效载荷对无动力运载器的上浮参数以及出水姿态有着严格的要求，而上浮参数以及出水姿态主要受无动力运载器的自身比重、质心与浮心位置、舵角以及外部海洋环境扰动等多种因素的影响。由于无动力运载器上浮以及出水过程中所受流体动力以及外部环境扰动较为复杂，故目前大多数研究都是采用模型试验、数学模型计算以及CFD 仿真与数学模型相结合的方法。例如，张天健等[1]采用模型试验与快速预报相结合的方法，对大深度浮力驱动式水下运载器的上浮运动进行了研究与分析；王占莹等[2]基于水下垂直发射水弹道理论模型并结合试验结果，对造成出水俯仰双态特征的机理进行了分析；蔡群等[3]应用CFD 技术计算运载器流体动力参数，从而建立运动学模型，分析了运载器壳体长细比、鳍板展弦比和发射速度对弹道参数的影响规律。田宝国等[4]建立了运载器在波浪扰动下的数学模型，利用Simulink 仿真了运载器受波浪扰动后的水弹道。目前对无动力运载器的主要研究情景为水平发射、垂直出水，或垂直上浮、垂直出水，而对无动力运载器垂直上浮、倾斜出水的情景以及改变自身比重、质心与浮心位置、舵角等对倾斜爬升式上浮参数和出水姿态影响的研究较少，且利用CFD 求解水动力系数后结合运动的一般方程进行计算的传统方法较为复杂。无动力运载器在倾斜爬升式上浮的过程中会出现大的攻角，进而表现出非线性特征，运动的一般方程难以满足要求。

本文拟基于STAR-CCM+的重叠网格技术、动态流体相互作用（Dynamic Fluid Body Interaction，DFBI）以及流体体积（Volume of Fluid，VOF）波模型，采用CFD 数值计算方法，对无动力运载器上浮过程进行动态仿真，研究无动力运载器的自身比重、质心与浮心位置、舵角以及释放初速对其倾斜爬升式上浮参数以及出水姿态的影响。研究结果可用于无动力运载器的总体布局和控制设计，并且为其他领域应用无动力运载器的可行性分析提供参考。

1 数值计算模型

1.1 无动力运载器模型简介

无动力载器模型如图1 所示。运载器采用回转体外形，其外形可以看作是由一条曲线绕中心轴扫描得到的，这条曲线称之为运载器的线型。运载器的线型分为3 部分，分别是头部曲线段、中间圆柱段和尾部曲线段。头部曲线段采用的是格兰韦尔单参数三次多项式平头线型，尾部曲线段采用的是格兰韦尔二次多项式尖尾线型[5]。

图 1 无动力运载器模型Fig. 1 Unpowered vehicle model

1.2 RANS 控制方程

笛卡儿坐标系下，对于黏性不可压缩流体，其连续性方程（质量守恒方程）和RANS 方程（动量守恒方程）的表达式分别为

式中：i,j=1,2,3；xi,xj为笛卡尔坐标分量；ρ为流体的密度；μ为动力黏性系数；ui，uj为速度分量的时间平均值；t为时间；ui′,uj′为速度分量的脉动；p为压力的时间平均值；为速度脉动乘积的时间平均值；Si为广义源项。

1.3 湍流模型

由于RANS 方程的未知量数目大于方程数目，方程不封闭，所以需要采用湍流模型来使RANS 控制方程封闭。本文采用目前应用最广泛的标准k−ε模型，该湍流模型是双方程模型，可对湍动能k和湍流耗散率 ε的传输方程进行求解，以确定湍流涡黏度。

湍流涡黏度 µt的计算公式为

式中：Cµ为 模型系数；fµ为阻尼函数；T为湍流时间尺度。

湍动能k和耗散率 ε的传输方程为：

上式中，各模型系数的取值分别为Cµ=0.09，σk=1.0， σε=1.3，Cε1= 1.44，Cε2=1.92。

1.4 VOF 多相模型

本文采用STAR-CCM+的VOF 多相模型来捕捉运载器在出水过程中气液面的复杂变化情况。交界面的相分布及其位置由体积分数 αj的场来描述，相i的体积分数定义为

式中：Vi为网格单元中相i的体积；V为网格单元的体积。网格单元中所有相的体积分数总和必须是1。

相i的分布由相质量守恒方程驱动：

式中：a为表面积矢量；v为质量平均速度；vdr,i为扩散速度；Sαi为相i的用户自定义源项； σt为湍流施密特数；Dρi/Dt为 相密度 ρi的材料或拉格朗日导数。

2 数值计算方法

2.1 计算域与边界条件设置

无动力运载器在倾斜爬升式上浮过程中会出现大攻角，进而表现出非线性特征，传统的数值预报方法难以满足要求。本文采用STAR-CCM+的重叠网格技术与DFBI，对运载器的上浮过程进行动态仿真。重叠网格技术是将复杂的流动区域分成几个几何边界较为简单的子区域，各个子区域中的计算网格独立生成，彼此存在着重叠、嵌套或覆盖关系，流场信息通过插值在重叠区域的边界上进行匹配和耦合[7]。

本文将整个计算区域划分为背景区域与重叠区域2 个部分，如图2 所示。背景区域相对于大地坐标系是静止的，重叠区域则随着运载器运动。背景区域为宽10 m，长、高均为65 m 的长方体，运载器浮心距离水面50 m。由于水面为气液两相交界面，VOF 方法要求交界面网格足够精细，所以在水面附近建立一个高2 m 的加密区，对气液两相交界面进行区域加密。背景域的边界包括速度入口和压力出口，速度入口的值设置为静水VOF 波速度的场函数，压力出口的值设置为静水VOF 波静压的场函数。速度入口和压力出口的体积分数均设置为静水VOF 波轻流体体积分数和静水VOF 波重流体体积分数的复合场函数。

图 2 计算域与边界条件设置Fig. 2 Computational domain and boundary condition settings

重叠区域如图3 所示，为高6 m，长、宽均为2 m 的长方体，对该区域进行各向同性加密。在重叠区域与背景区域的交界处建立重叠网格界面，背景网格与重叠网格通过重叠网格交界面来实现数据的传递和网格的更新。运载器表面为无滑移壁面，为保证壁面边界层网格的生成，采用棱柱层网格对壁面进行划分。

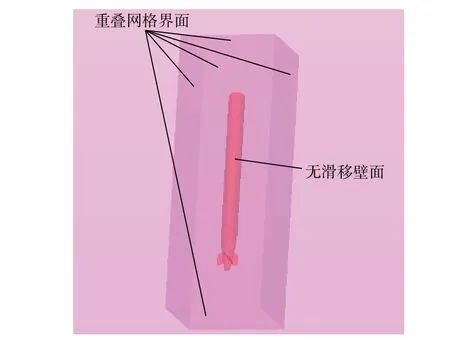
图 3 重叠区域Fig. 3 Overlapping grid area

2.2 网格划分

流体介质为15 ℃海水，密度ρ=1 025.91 kg/m3，动力黏度µ=1.005×10−3Pa·s， 湍流模型选择k−ε模型， ∆y+=20。由文献[8]计算得到，运载器表面棱柱层第1 层厚度为4.344 0×10−4mm，棱柱层总厚度为9.467 5 mm，棱柱层延伸系数为2.894 6，面网格的最小尺寸为5 mm。采用切割体网格对背景区域和重叠区域进行网格划分，如图4 和图5 所示，它们分别为运载器上浮过程和出水过程某时刻的重叠网格。

图 4 运载器上浮过程某时刻的重叠网格Fig. 4 Overlapping grid at some point in the vehicle's floating process

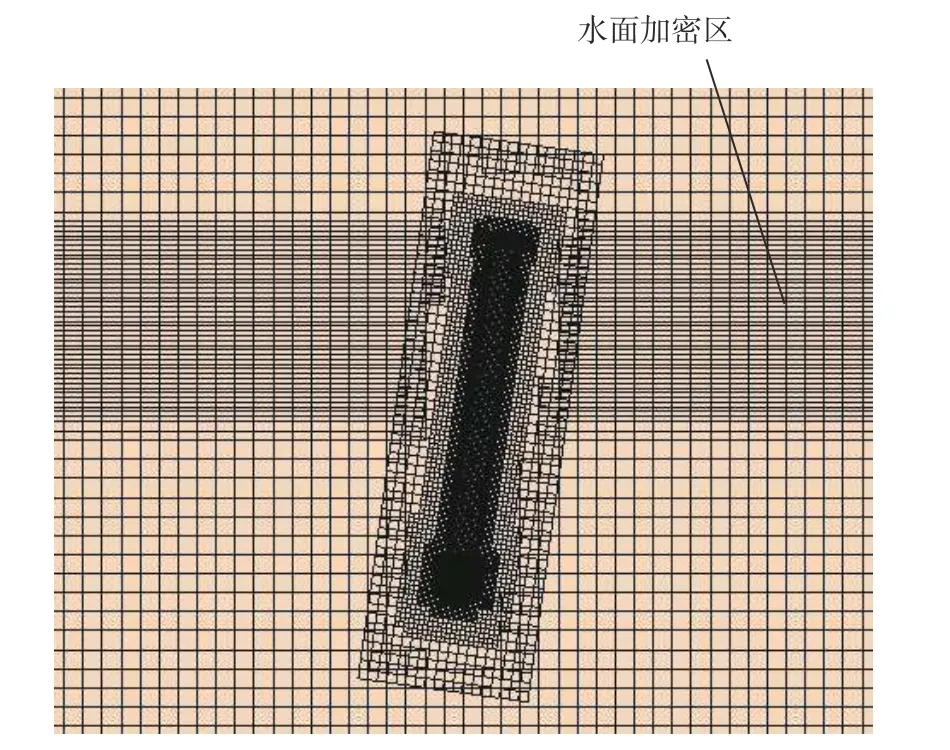
图 5 运载器出水过程中某时刻的重叠网格Fig. 5 Overlapping grid at some point during the water-exit process of the vehicle

2.3 数值计算方法验证

为验证上述数值计算方法的正确性，本文首先采用REMUS 100 模型试验数据进行理论验证。如图6 所示，该模型主体为回转体外形，回转体最大直径为191 mm，特征长度为1 332.7 mm，由拖曳水池试验测得该模型的阻力系数cd=0.118 347[9]。采用上述数值计算方法，对该模型的垂直上浮过程进行数值预报。由理论分析可知，当该模型垂直上浮的阻力等于净浮力时，上浮速度达到最大，之后开始以最大速度匀速上浮。最大速度的计算公式为

图 6 REMUS 100 模型Fig. 6 REMUS 100 model

式中： ∆G为净浮力；Af为最大投影面积；cd为该模型的阻力系数。

对该模型净浮力分别为0.05VR，0.10VR和0.15VR条件下的垂直上浮过程进行数值计算，其中VR为模型的排水重量。最大垂直上浮速度的数值计算结果与理论值对比情况如表1 所示。由表1 可知，数值计算的精度满足工程应用要求，这也验证了该数值计算方法的准确性。

表 1 最大垂直上浮速度的数值计算结果与理论值对比情况Table 1 Comparison of maximum vertical floating velocity between numerical calculation results and theoretical values

为验证上述数值计算方法对于运载器大攻角、非线性、倾斜式无动力上浮运动模拟的计算精度，本文采用缩比模型水池试验(图7)对数值计算方法进行了验证。试验水池水深8.5 m，缩比模型的直径为160 mm，长度为1 925 mm，总排水体积为32.69 kg，整体衡重之后的净浮力为6.58 kg，将坐标系原点设于压力传感器处，浮心的位置为（722.211 mm，−0.003 mm，0 mm），质心位置为（555.959 mm，18.211 mm，0.209 mm）。分别设计了3 种试验方案，将运载器在舵角分别为10°，20°以及30°情况下无动力上浮时测得的数据与仿真计算结果进行了对比。

图 7 缩比模型试验Fig. 7 Scale model test

图8～图13 分别给出了试验模型在舵角为10°，20°以及30°条件下无动力上浮过程中纵倾角与垂直位置的试验测量数据与仿真计算值的对比结果。由图中可以看出，试验模型在初始释放的一段时间内试验测量的纵倾角存在一定的波动，与仿真计算值有一定的偏差，但随着不断上浮，试验值与计算值的变化趋势基本一致，数值上也逐渐靠近。其主要原因是在运载器释放的一瞬间，力和力矩将施加于连续体，并且可能会产生冲击效应。为避免这种情况，在数值计算时设置了1 s 的缓冲时间，在整个间隔内会按比例施加力和力矩，从而减少冲击效应，所以仿真计算曲线的变化初期是比较平缓的。垂直位移时历曲线的试验测量数据与仿真计算值吻合较好，总体变化趋势也大体相同，数值上非常接近。综上所述，本文数值计算方法的精度满足工程应用的需求。

图 8 无动力上浮过程中纵倾角时历曲线（10°舵角）Fig. 8 Time histories of the longitudinal angle in unpowered floating process （10° rudder angle）

图 9 无动力上浮过程中垂直位移时历曲线（10°舵角）Fig. 9 Time histories of the vertical displacement in unpowered floating process（10° rudder angle）

图 10 无动力上浮过程中纵倾角时历曲线（20°舵角）Fig. 10 Time histories of the longitudinal angle in unpowered floating process （20° rudder angle）

图 11 无动力上浮过程中垂直位移时历曲线（20°舵角）Fig. 11 Time histories of the vertical displacement in unpowered floating process （20° rudder angle）

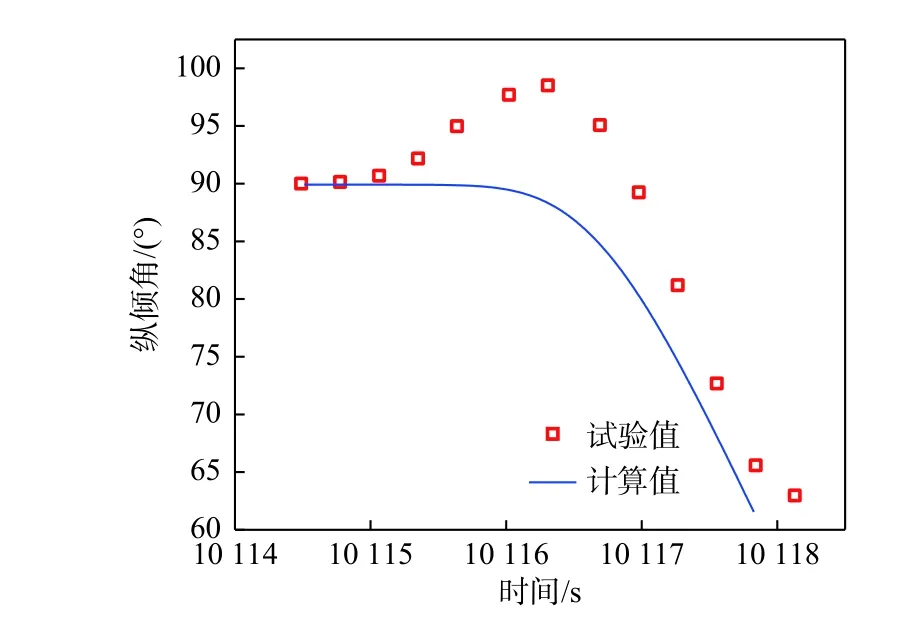
图 12 无动力上浮过程中纵倾角时历曲线（30°舵角）Fig. 12 Time histories of the longitudinal angle in unpowered floating process （30° rudder angle）

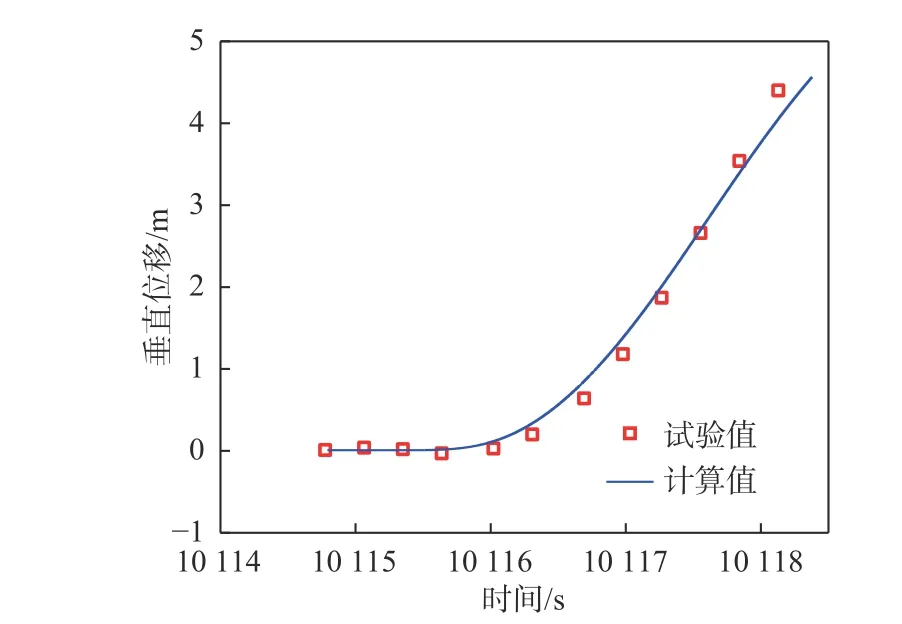
图 13 无动力上浮过程中垂直位移时历曲线（30°舵角）Fig. 13 Time histories of the vertical displacement in unpowered floating process（30° rudder angle）

3 计算结果与分析

3.1 质心与浮心之间的轴向距离对上浮参数的影响

当运载器快要到达水面时，需要使运载器开始倾斜爬升式上浮，从而满足有效载荷对运载器出水姿态的要求。本文采用上述数值计算方法对运载器倾斜爬升上浮过程进行了动态仿真。在运载器浮心距离水面50 m 时将其竖直释放，其初始速度为vx=5 m/s，vy= 0，vz=0，净浮力为0.20V0，水平舵角偏转30°，质心与浮心之间的径向距离为0D，对比质心与浮心之间的轴向距离分别为0.05L，0.15L和0.25L条件下运载器的上浮参数。其中：V0为运载器的排水重量；L为运载器的特征长度；D为运载器的特征直径。

图14～图16 所示为运载器的纵倾角、角速度和角加速度时历曲线。由图14 可以看出：当运载器质心与浮心之间的轴向距离为0.05L时，运载器被释放后，其纵倾角在减小到0°后开始往复摆荡，最后运载器稳定上浮时的纵倾角为0°；当运载器质心与浮心之间的轴向距离为0.15L和0.25L时，运载器被释放后，其纵倾角逐渐达到稳定后开始倾斜爬升式上浮。对比可知，运载器质心与浮心之间的轴向距离越大，最终达到稳定时的纵倾角越大。当运载器质心与浮心之间的轴向距离为0.25L时，纵倾角稳定在30°附近。由图14～图16可知，由于初速度以及舵角偏转的角度相同，所以运载器在被释放后的一段时间内，角加速度、角速度以及纵倾角的变化趋势相同，运载器达到稳定时的角速度和角加速度都趋向于0。同时，当质心与浮心之间的轴向距离为0.25L时，运载器达到稳定所用的时间最短，且角加速度始终小于0。

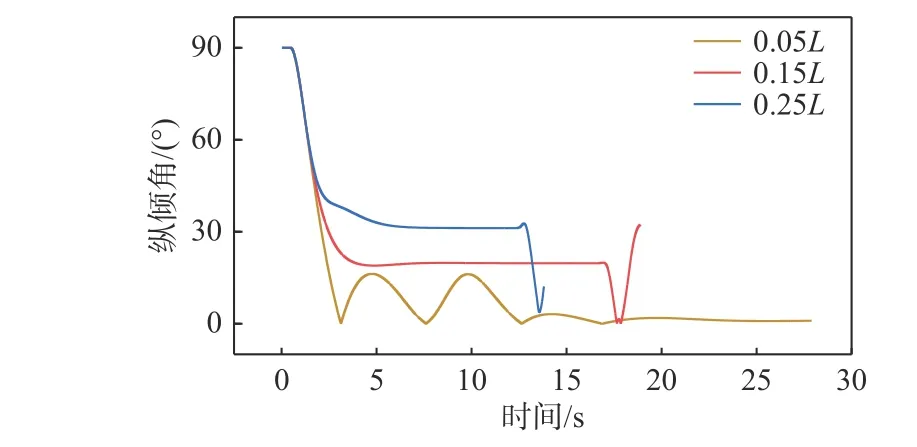
图 14 不同质心与浮心间轴向距离时的纵倾角时历曲线Fig. 14 Time histories of pitch angle at different axial distances between the mass and buoyancy centers

图 15 不同质心与浮心间轴向距离时的角速度时历曲线Fig. 15 Time histories of angular velocity at different axial distances between the mass and buoyancy centers

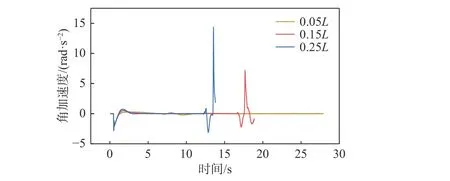
图 16 不同质心与浮心间轴向距离时的角加速度时历曲线Fig. 16 Time histories of angular acceleration at different axial distances between the mass and buoyancy centers

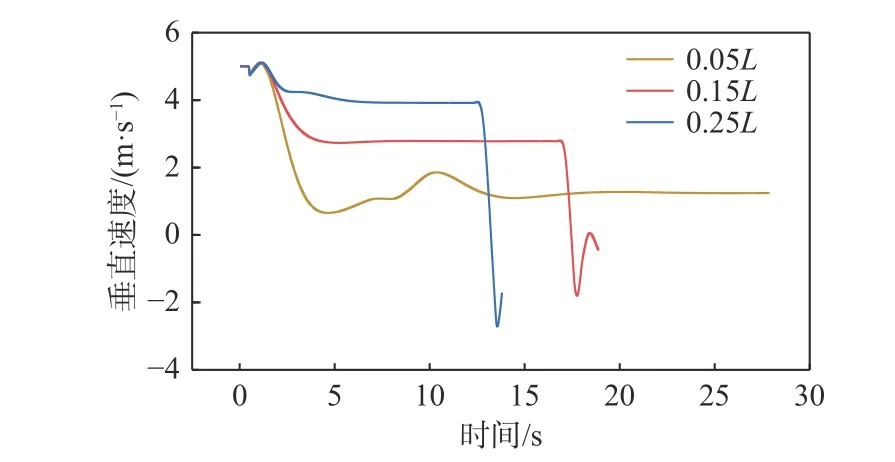
图 17 不同质心与浮心间轴向距离时的垂直速度时历曲线Fig. 17 Time histories of vertical speed at different axial distances between the mass and buoyancy centers

图 18 不同质心与浮心间轴向距离时的水平速度时历曲线Fig. 18 Time histories of horizontal speed at different axial distances between the mass and buoyancy centers

图17 和图18 所示为运载器的垂直速度和水平速度时历曲线。由图17 可知，当运载器被释放后，其在水平舵的作用下开始倾斜，垂直速度因此逐渐减小，直至到达稳定上浮状态。对比发现，质心与浮心之间的轴向距离越大，运载器倾斜爬升稳定上浮的垂直速度就越大，到达水面的时间也就越短。由图18 可知，当运载器质心与浮心之间的轴向距离为0.15L和0.25L时，二者倾斜爬升稳定上浮的水平速度几乎相同，均在3.5 m/s附近。由此可知，当质心与浮心之间的轴向距离为0.25L时，运载器达到稳定所需的时间最短，倾斜爬升的纵倾角最大，垂直速度最大，到达水面所需的时间最短，且横向漂移的距离也最短。

3.2 质心与浮心之间的径向距离对上浮参数的影响

在运载器浮心距离水面50 m 时将其竖直释放，初 始 速 度 为vx=5 m/s，vy= 0，vz=0，净 浮 力 为20%V0，水平舵角偏转30°，质心与浮心之间的轴向距离为0.25L，对比质心与浮心之间的径向距离分别为0.05D，0.15D和0.25D条件下运载器上浮的运动状态。

图19～图23 所示为运载器的纵倾角、角速度、角加速度、垂直速度和水平速度时历曲线。由图19 可以看出，三者纵倾角随时间变化的规律几乎相同，且最终都稳定在30°附近，可见质心与浮心之间的径向距离对运载器倾斜爬升到达稳定状态时的纵倾角影响较小。由图20 和图21 可以看出，当径向距离为0.25D时，运载器的角加速度和角速度变化范围最大。由图22 和图23 可以看出：运载器质心与浮心之间的径向距离越小，垂直上浮的速度就越快，到达水面所需的时间就越短；水平速度越小，横向漂移的距离也越短。

图 19 不同质心与浮心间径向距离时的纵倾角时历曲线Fig. 19 Time histories of pitch angle at different radial distances between the mass and buoyancy centers

图 20 不同质心与浮心间径向距离时的角速度时历曲线Fig. 20 Time histories of angular velocity at different radial distances between the mass and buoyancy centers

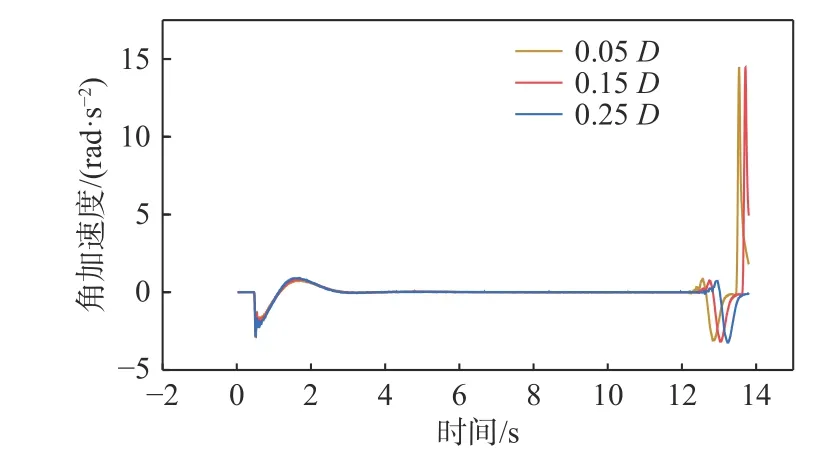
图 21 不同质心与浮心间径向距离时的角加速度时历曲线Fig. 21 Time histories of angular acceleration at different radial distances between the mass and buoyancy centers

图 22 不同质心与浮心间径向距离时的垂直速度时历曲线Fig. 22 Time histories of vertical speed at different radial distances between the mass and buoyancy centers

图 23 不同质心与浮心间径向距离时的水平速度时历曲线Fig. 23 Time histories of horizontal speed at different radial distances between the mass and buoyancy centers

3.3 净浮力对上浮参数的影响

在运载器浮心距离水面50 m 时将其竖直释放，初始速度为vx=5 m/s，vy= 0，vz=0，水平舵角偏转30°，质心与浮心之间的轴向距离为0.25L，径向距离为0.05D，对比净浮力分别为0.10V0，0.15V0和0.20V0条件下运载器上浮的运动状态。

图24 和图25 所示为运载器的纵倾角和角速度时历曲线。由图24 可知，净浮力越小，运载器稳定倾斜爬升时的纵倾角越大，当净浮力为0.15V0时，运载器纵倾角稳定在45°附近。同时由图24 和图25 可以发现，当净浮力为0.10V0时，运载器被释放后，在水平舵的作用下，角速度为负值，纵倾角减小，当达到最小值后，角速度变为正值，纵倾角开始增加并逐渐达到稳定。所以，当净浮力为0.10V0时，运载器在到达稳定倾斜爬升状态前会经历一个回摆过程。

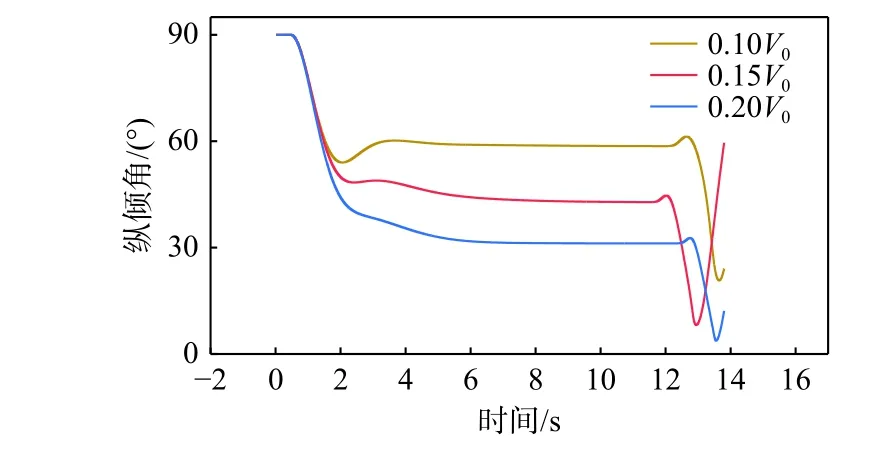
图 24 不同净浮力时的纵倾角时历曲线Fig. 24 Time histories of pitch angle at different net buoyance

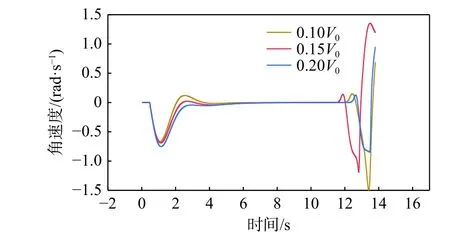
图 25 不同净浮力时的角速度时历曲线Fig. 25 Time histories of angular velocity at different net buoyance

图26 和图27 所示为运载器的垂直速度和水平速度时历曲线。由图26 可知：并非净浮力越大，运载器上浮的垂直速度就越快；当净浮力为0.20V0时，上浮的垂直速度反而最小。这主要是由于运载器净浮力越大，纵倾角就越小，所以运载器垂直方向的阻力越大。当净浮力为0.15V0时，垂直上浮的速度最大。由图27 可知，运载器的净浮力越大，水平速度就越大，横向漂移的距离也就越远。

图 26 不同净浮力时的垂直速度时历曲线Fig. 26 Time histories of vertical speed at different net buoyance

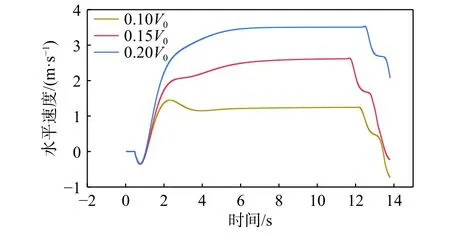
图 27 不同净浮力时的水平速度时历曲线Fig. 27 Time histories of horizontal speed at different net buoyance

3.4 舵角对上浮参数的影响

在运载器浮心距离水面50 m 时将其竖直释放，初 始 速 度 为vx=5 m/s，vy= 0，vz=0，净 浮 力 为0.15V0，质心与浮心之间的轴向距离为0.25L，径向距离为0.05D，对比水平舵角分别为10°，20°和30°条件下运载器上浮的运动状态。

图28～图30 所示分别为运载器的纵倾角、角速度和角加速度时历曲线。由图28 可知，水平舵角越大，运载器稳定倾斜爬升时的纵倾角越小。当舵角为20°和30°时，运载器的纵倾角均稳定在45°附近。所以，当舵角增大到一定角度后，对运载器纵倾角变化的影响逐渐减小。由图29 和图30 可知，运载器水平舵偏转的角度越大，产生的偏转力矩越大，所以角加速度和角速度的绝对值越大。

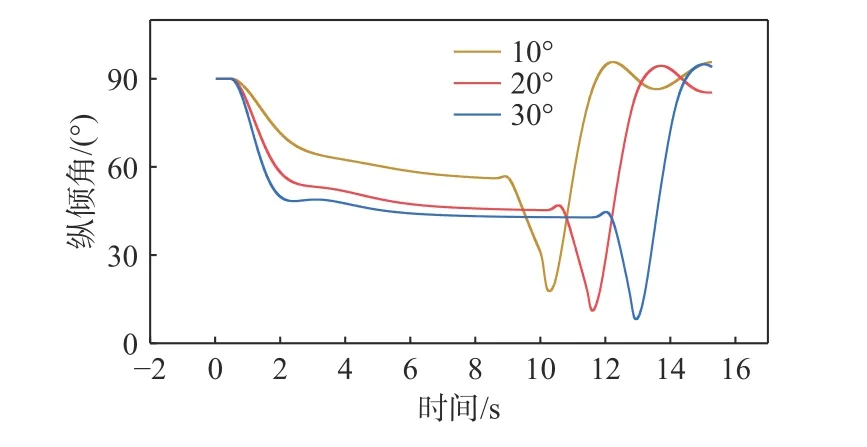
图 28 不同水平舵角时的纵倾角时历曲线Fig. 28 Time histories of pitch angle at different horizontal rudder angles

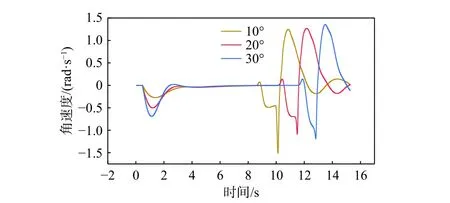
图 29 不同水平舵角时的角速度时历曲线Fig. 29 Time histories of angular velocity at different horizontal rudder angles

图 30 不同水平舵角时的角加速度时历曲线Fig. 30 Time histories of angular acceleration at different horizontal rudder angles

图31 所示为运载器的垂直速度时历曲线。由图31 可知，舵角越大，运载器上浮的垂直速度越小，到达水面所需的时间越长。虽然舵角为20°和30°时，运载器倾斜爬升时的纵倾角均稳定在45°附近，但舵角为20°时，上浮的垂直速度更大，稳定在5 m/s 左右。

图 31 不同水平舵角时的垂直速度时历曲线Fig. 31 Time histories of vertical speed at different horizontal rudder angles

3.5 初速度对上浮参数的影响

在运载器浮心距离水面50 m 时将其竖直释放，设置净浮力为0.20V0，质心与浮心之间的轴向距离为0.25L，径向距离为0.05D，舵角为20°，对比 在 释 放 初 速vy= 0，vz=0 而vx分 别 为5，6.87 和10 m/s 条件下运载器上浮的运动状态。

图32～图34 所示分别为运载器的纵倾角、角速度、角加速度、垂直速度和水平速度时历曲线。由图中可以看出，运载器在3 种初始垂直速度条件下最终达到的稳定状态相同，无论是纵倾角、垂直速度还是水平速度。由此可知，运载器的初始速度并不会影响稳定状态的上浮参数。由图33 和图34 可知，运载器释放的初始速度越大，角速度和角加速度就越大，纵倾角的变化范围也就越大。由图35 和图36 可知，运载器释放的初始速度为vx=10 m/s 时，运载器在逐渐达到稳定倾斜爬升的过程中，垂直速度的最小值低于稳定时的垂直速度，水平速度的最大值高于稳定时的水平速度。所以，当运载器释放的初始速度大于运载器的最大上浮垂直速度时，到达水面的时间反而会更长，横向漂移的距离也会更远。

图 32 释放初速 vy =0， vz= 0， vx分别为5，6.87 和10 m/s 时的纵倾角时历曲线Fig. 32 Time histories of pitch angle at initial launch velocity: vy =0, vz= 0, vx=5, 6.87 and 10 m/s

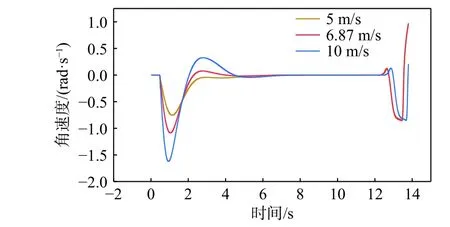
图 33 释放初速 vy =0， vz= 0， vx分别为5，6.87 和10 m/s 时的角速度时历曲线Fig. 33 Time histories of angular velocity at initial launch velocity: vy =0, vz= 0, vx=5, 6.87 and 10 m/s

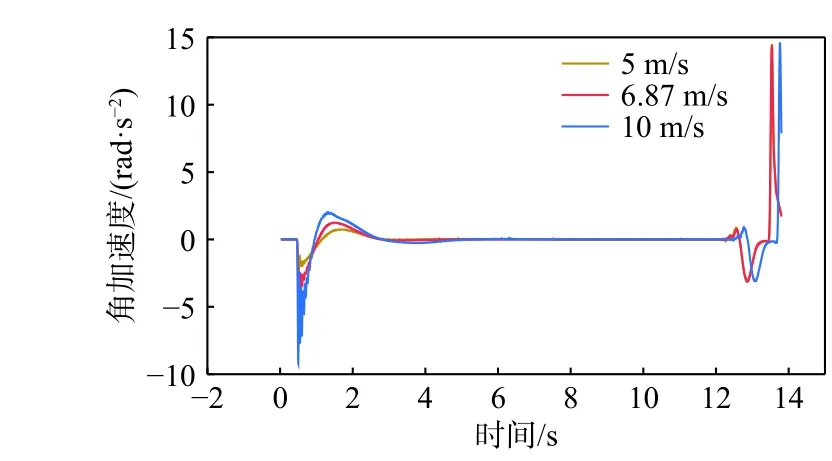
图 34 释放初速 vy =0， vz= 0， vx分别为5，6.87 和10 m/s 时的角加速度时历曲线Fig. 34 Time histories of angular acceleration at initial launch velocity: vy =0, vz= 0, vx=5, 6.87 and 10 m/s

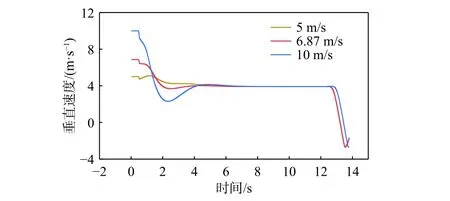
图 35 释放初速 vy =0， vz= 0， vx分别为5，6.87 和10 m/s 时的垂直速度时历曲线Fig. 35 Time histories of vertical speed at initial launch velocity: vy =0, vz= 0, vx=5, 6.87 and 10 m/s

图 36 释放初速 vy =0， vz= 0， vx分别为5，6.87 和10 m/s 时的水平速度时历曲线Fig. 36 Time histories of horizontal speed at initial launch velo- city: vy =0, vz= 0, vx=5, 6.87 and 10 m/s

4 结 论

本文基于STAR-CCM+的重叠网格技术、DFBI以及VOF 波模型，采用CFD 数值计算方法，对无动力运载器上浮过程进行了动态仿真，研究了无动力运载器自身比重、质心与浮心位置、舵角以及释放初速对倾斜爬升式上浮参数以及出水姿态的影响，得到以下结论：

1） 基于STAR-CCM+重叠网格技术、DFBI 以及VOF 波模型的数值计算方法可以很好地模拟运载器无动力上浮过程，避免了利用CFD 求解水动力系数，结合运动一般方程进行计算的传统方法所带来的复杂性。与REMUS 100 模型垂直上浮理论计算值以及缩比模型倾斜上浮水池试验结果的对比表明，本文数值计算方法的计算精度满足工程应用需求。

2） 质心与浮心之间的轴向距离越大，运载器最终达到稳定的纵倾角越大，达到稳定所需的时间越短，倾斜爬升稳定上浮的垂直速度越大，到达水面所需的时间越短。

3） 运载器质心与浮心之间的径向距离对倾斜爬升到达稳定状态时的纵倾角影响较小，质心与浮心之间的径向距离越小，垂直上浮的速度越快，到达水面所需的时间越短，水平速度越小，横向漂移的距离也越短。

4） 净浮力越小，运载器稳定倾斜爬升时的纵倾角越大。当净浮力为0.15V0时，运载器纵倾角稳定在45°附近；当净浮力为0.10V0时，运载器在到达稳定倾斜爬升状态前会经历一个回摆过程；并非净浮力越大，运载器上浮的垂直速度越快，当净浮力为0.20V0时，上浮的垂直速度反而最小。

5） 水平舵角越大，运载器稳定倾斜爬升时的纵倾角越小。当舵角为20°和30°时，运载器的纵倾角均稳定在45°附近；同时，水平舵角越大，运载器上浮的垂直速度越小，到达水面所需的时间越长。

6） 运载器的释放初速并不会影响倾斜爬升稳定状态时的上浮参数，当运载器释放的初始速度大于运载器的最大上浮垂直速度时，到达水面的时间反而会更长，横向漂移的距离也会更远。