船舶在波浪上纵向运动与控制研究综述

孙一方，宗智*,2,3，姜宜辰,2

1 大连理工大学 船舶工程学院，辽宁 大连 116024

2 高新船舶与深海开发装备协同创新中心，上海 200240

3 辽宁深海浮动结构工程实验室，辽宁 大连 116024

0 引 言

随着世界各国经济和军事的发展，人们对船舶快速性和耐波性的要求越来越高，诸如深V 单体船[1]、小水线面双体船[2]、穿浪双体船[3]、高速三体船[4]等高性能船舶也应运而生。但是，在高速航行或者遭遇恶劣海况时，高性能船容易产生大幅度的摇荡运动，引起失速、艏部砰击、船体结构损坏、乘员晕船[5]等，对船上设备的运行和航行安全造成不利的影响。因此，为了保证其在高速、高海况航行时依然具有良好的耐波性、快速性和稳性等综合性能，在船体上安装减摇附体成为一种重要手段[6]。目前，高性能船上安装的减摇附体主要包括半潜艏、T 型翼、艉压浪板和扰流板等。

半潜艏由日本学者木原和之在上世纪80 年代中期提出[7]，安装于船艏底部。模型试验和实船测试表明，加装半潜艏可以有效降低运动响应峰值区域附近的纵摇角和艏加速度，降幅高达40%。但是半潜艏排水量约占全船的15%，船舶湿表面积会增加约10%。此外，半潜艏会使船艏变大，增加船舶阻力，这与多体高速船的设计目标不符，因此高速多体船上很少有这种设计。

T 型翼属于水翼的一种。该翼型最早出现于20 世纪90 年代，安装于船艏底部龙骨下方[8]，由水平翼和垂直翼两部分组成。在船舶航行时，会有效增加船舶的纵向阻尼，继而降低纵摇以及垂荡的运动幅度。同时调整其水平翼的摆角可以产生升力，增加减摇效果。与传统水翼相比，安装在船底的T 型翼有着更大的浸深，产生的湍流远离船底板，可避免产生空泡或吸气效应，增阻效果不明显。引入可回收装置可以大大减少其维护成本，延长使用寿命。

艉压浪板于上世纪80 年代开始应用于美军高速水面舰艇[9]，它通过改善艉后兴波及增加船舶虚长度来减小兴波阻力。实际应用表明，艉压浪板有很好的减阻效果，同样航速下，可将发动机转速降低19%，最高航速增加1 kn。除了减阻效果外，艉压浪板也有一定的减摇效果。西班牙马德里大学于1997 年对艉压浪板的减摇效果进行了船模试验，结果表明，在不规则波下使用艉压浪板会使船模的纵向运动幅度降低10%左右。

艉扰流板是上世纪90 年代提出的一种新型减摇设备[10]，其安装于船舶艉部，对其前方一定区域内的水流起到阻滞作用，继而改变流场以及船底部压力分布，产生升力来调整船舶航行时的纵倾角度，达到改善航态和降低船舶阻力的作用。与压浪板相似，扰流板也有一定的减摇效果。目前艉压浪板大多应用在小型游艇上，在大型高速船舶应用方面主要处于科学研究和技术储备阶段。

将主动控制程序引入减摇附体控制系统可以随着船舶航态的改变实时地对以上附体进行控制（自动调节T 型翼和艉压浪板的摆角、艉扰流板的伸出长度等），可以显著增加附体的恢复力（矩），提高其减摇效果。世界上首个装配于双体船的水翼自动控制系统由挪威Fjellstrand 公司于1991 年推出[11]，该系统可以实时监控船舶运动并通过调整水翼的摆角来降低船艏的垂向运动。实船试验表明，在3 m 波高下使用90%的动力即可保持40 kn 的高航速。该系统已在多艘实船上应用。1992 年，挪威Harding 公司为一艘35 m 双体船加装了3 副可控水翼[12]，分别布置于双体船槽道中央以及2 个片体后方，实际应用表明，该系统可以有效提高双体船的适航性。21 世纪以来，Esteban 等[13]对T 型翼和艉压浪板的组合进行了研究，并将其安装于高速渡轮船模上进行了试验，试验结果表明，使用主动式T 型翼和艉压浪板可使船的垂向加速度降低65%。此外，澳大利亚INCAT 公司为美国的JHSV 双体船和西班牙的穿浪双体船都设计了航态控制系统（Ride Control System, RCS），该系统由2 个艉扰流板和1 个可收回的艏部T 型翼组成，以控制高海况下双体船的纵摇和垂荡运动。

总体而言，智能化是未来船舶发展的重要课题，要求船舶的附体可以根据实际遭遇的海况而实时改变位置或摆角。对于减摇附体控制系统的研究主要包含了附体控制策略和船舶运动预报2 大部分，主要采用数值计算、水池试验和实船试验用这3 种方式。本文将对船舶在波浪上运动与控制的发展进行综述，包含数值计算和模型试验2 大部分，并在最后对相关研究进行展望。

1 数值计算研究

1.1 船舶运动的计算方法

对船舶耐波性数值计算的研究始于20 世纪50 年代，Korvin-Kroukovsky[14]在空气动力学中细长体理论的基础上将船舶势流理论中的三维问题化简为二维问题，初期只能计算迎浪情况下的升沉和纵摇运动。随后，Tasai[15]，Grim 和Schenzle[16]将该方法推广到了斜浪和横向运动中，即普通切片法（Ordinary Strip Method, OSM）。20 世纪70 年代，Salvesen 等[17]在此基础上提出了基于细长体假设和高频低速假设的Salvesen-Tuck-Faltinsen（STF）切片理论，引入了绕射势，以考虑船体对入射波流场的影响，继而实现了船舶在波浪上迎浪和斜浪下各种摇荡运动（除纵荡外）的求解。鉴于传统切片理论仅适合于计算低弗汝德数条件下船体的运动，Chapman[18]提出了高速细长体理论（2.5D 理论），此后Faltinsen 和Zhao[19]将其推广到可以求解任意细长体船型在高速下的水动力问题，该方法在切片理论的基础上保持了三维有航速的自由面条件，以反映航速的影响。Duan 等[20]将2.5D 理论的定解问题看作二维时域的物面非线性问题，通过格林函数的记忆效应来考虑自由面的三维效应，提高了2.5D 理论求解水动力问题的效率和稳定性。Ma 等[21]采用时域格林函数方法求解斜浪中单体和多体船的运动响应和波浪载荷，将计算结果与模型试验结果和STF 方法进行了比较，并将频域内线性2.5D 理论进行扩展，求解了船舶航行于迎浪大幅规则波中时的垂向非线性运动和波浪诱导载荷响应。这些基于势流理论的方法有着计算效率高的优点，但其忽略了黏性的作用，未考虑船舶运动时大幅度的运动、船体附近破波现象等非线性因素，而这些因素有时会对船舶在波浪上的运动产生显著影响。

计算流体力学（Computational Fluid Dynamics，CFD）是求解黏性流场中船舶运动的重要方法，其过程主要是通过不同的湍流模型求解雷诺时均方程（Reynolds Averaged Navier-Stokes, RANS）的方法，求解思想是将计算域划分为若干网格，在网格上对方程进行离散，将偏微分方程简化为代数方程组。上世纪70 年代时大多是在势流理论的基础上利用边界层理论来计算粘流。1978 年，Abdelmeguid 等[22]基于传热问题求解了船舶的三维黏性绕流问题。1980 年代，对黏性流的计算逐渐发展起来。Patel[23]通过流场试验的测量结果，从物理上分析阐明了船舶CFD 数值方法应采用何种近似方法，该阶段的CFD 是基于简化的RANS 方程。上世纪90 年代以来，随着计算机技术的进步，大量基于CFD 的软件被用于求解船舶耐波性问题，包括船艏破波[24]、船舶数值水池、黏性流场中的船舶运动[25]、带附体和螺旋桨船舶附近的流场[26]等。Castiglione 等[27]完成的数值预报与试验结果的对比研究表明，非稳态RANS（Unsteady RANS，URANS）方法可以有效模拟高航速和复杂海况下的多体船运动问题。Deng 等[28]、梁洪光[29]、邱永吉[30]等均采用CFD 方法计算了被动式T 型翼对三体船阻力和耐波性的影响。但由于船舶附体（如舭龙骨、T 型翼）的边缘部分对网格质量要求较高，CFD 方法需要大量的计算时间。

Yeung 等[31]提出了自由表面随机涡方法（Free Surface Random Vortex Method, FSRVM），结合船舶2.5D 理论以及离散涡法，推导出了适用的非线性自由水面边界条件、瞬时水下物面上不可穿透和无滑移条件、边界积分方程和载荷的计算公式，建立了可以模拟多体高速船在波浪中多自由度运动响应的数值模型[32]，在时域内可预报多体高速船在迎浪或斜浪下的垂荡和纵摇运动、自由表面兴波以及运动控制装置的减摇减荡作用。Jiang等[33]在整体模型中建立了各个运动控制装置的子模型，子模型根据多体船状态计算运动控制装置作用于多体船的载荷，并将载荷传递到多体船总的运动方程中。该方法提出的数值模型采用了一种虚拟的扩展速度概念，用来模拟船舶航速对二维平面流体的影响。图1 和图2 所示为二维计算平面模型和扩展速度的示意图。图中：pex为施加于某一区域自由表面上用于造波的额外压强分布函数；βh为入射波的无旋复速度势；∂Df为自由表面边界；∂Db为物面边界；∂D∑为无穷远边界；（xbO,i，ybO,i）为动坐标系下点的坐标；Unχ为船体表面某点的法向向量沿船长方向的速度分量。船舶在穿过某一固定平面时，与平面相切的船体轮廓会不断发生变化，当前时刻物面上的流体微团会被推至下一时刻的物面上，以满足不可穿透条件。该方法以无网格的方式，高效地求解了这一复杂问题，有效克服了数值黏性和畸形单元等问题。作为一种降阶方法，其与传统网格化计算流体力学方法相比，在计算时间上具有很大优势，同时保持了较高的计算精度。

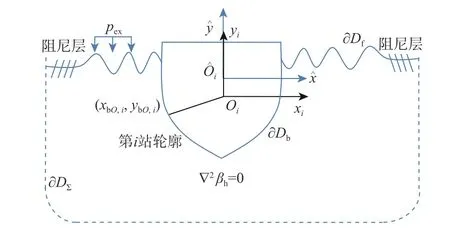
图 1 二维计算平面模型Fig. 1 The model of a two-dimensional computational plane

1.2 控制信号的研究

附体减摇系统控制信号的研究是整个减摇系统的基础，直接决定了整套控制系统的作用效果。因此，对比采用不同控制信号控制T 型翼的摆角对船舶运动的减摇效果显得非常重要。Fang 等[34]针对小水线面双体船（Small Water-plane Area Twin Hull, SWATH）船型，提出采用纵摇角速度信号控制稳定鳍的摆角来减小船在航行时的纵摇角。2012 年，孔卫[35]基于切片理论对某深V 型快速渡轮进行了水动力求解，其分别采用纵摇角速度信号和垂荡速度信号这2 种控制策略实现了摆角在0°，15°和30°这3 个值的实时变化，并计算了航速在20 和40 kn 时上述2 种控制策略下船的垂荡和纵摇响应。结果表明，采用纵摇角速度信号控制策略对纵摇角的减摇更为明显，而采用垂荡速度信号控制策略对垂荡运动的减摇更明显。刘冰[36]采用势流理论对某高速双体船进行了水动力计算并构建了T 型翼和扰流板的升力模型，在摆角的控制策略方面，利用仿真技术，采用纵摇角、纵摇角速度和纵摇角加速度联合控制的方式计算了减摇效果，结果表明，采用主动控制策略后垂荡与纵摇的最大减摇幅值可达50%。2017年，Javad 等[37]基于静水中的模型试验提出了一种非线性控制方法（即当模型运动方向改变时立即让T 型翼和压浪板的转角转到反向最大值，类似于阶跃控制），并将其与采用纵摇角速度信号、垂荡速度信号控制T 型翼和艉压浪板的摆角时船模在规则波上的运动进行对比，试验结果发现，采用非线性控制具有更好的减摇效果，并且采用垂荡速度控制附体摆角更有利于控制船模的垂荡位移；相应的，采用纵摇角速度控制附体摆角更适合减少船模的纵摇响应。2018 年，孙一方等[38]以Wigley船型为研究对象，基于自由表面随机涡法计算了时域中不同航速下船的垂荡、纵摇和艏加速度值。通过对力矩控制策略进行分析，采用纵摇角、角速度和角加速度分别对T 型翼摆角进行控制，提出并计算了各工况下各控制信号的增益系数，将计算结果与无T 型翼的裸船模进行了对比，试验结果表明，低速时采用纵摇角信号作为T 型翼的控制信号具有更好的减摇效果，而在中、高速情况下采用纵摇角速度信号控制T 型翼的摆角在多数情况下减摇效果更好。

1.3 船舶纵向运动控制方法研究

Ziegler 和Nichols[39]设计了比例、积分、微分（PID）控制器，并将其应用于实际工业生产中。因其具有稳定、可靠的特点，被广泛应用于船舶的运动控制领域中[40]。1995 年，Haywood 等[41-42]设计完成了高速单体船的航态控制系统，包含T 型翼、水翼、艉压浪板、扰流板等减摇附体，并对其制造成本、易用性、维护和制造材料等进行了总结分析[43]。鉴于PID 控制需要根据不同工况（航速、海况等因素）实时改变控制增益系数，需要消耗大量的人力和时间成本，傅京孙提出了“智能控制”[44]这一概念，即实现无需人工干预、由机器自主达成预定目标的自动控制。此后，神经网络、遗传算法和模糊控制等智能控制算法相继出现并应用到了船舶运动控制领域中。Akhyar和Omatu[45]针对传统PID 控制的不足，采用了BP 神经网络方法来整定PID 控制参数。Fang 等[40]将自适应神经网络控制器引入到了减摇鳍对船舶横摇的控制系统中，结果表明，与遗传算法获得的PID 控制系数相比，基于神经网络的控制器在规则波和不规则波中的减横摇效果更好。

1.3.1 国外研究进展

1994 年，Sørensen 等[46]基于无源系统理论开发了一种分布式航态控制系统（Distributed Ride Control System, DRCS），并设计了比例压力反馈控制器，以提高附体对船舶垂荡和纵摇加速度的阻尼作用，改善船舶的耐波性。Giron-Sierra 等[47-48]利用PID 控制实现了对高速单体船上装备T 型翼和艉压浪板的船模的控制，测试了不同控制参数下PID 控制器的控制效果，仿真计算表明，加装主动控制系统的减摇附体可以比被动控制情况下减摇效果提高25%。随后，Esteban 等[49]利用主动控制艉板和T 型翼对某高速单体渡轮的垂向加速度进行了限制，通过PID 控制仿真得到了不同控制系数时垂向加速度最大值（WVA）的减摇效果，发现在较高的比例增益下，积分控制项对结果影响不大，于是将PID 控制简化为了PD 控制。2001 年，该团队在通过CFD 计算船舶水动力系数的基础上，建立了波浪、力、运动之间的传递函数，使用Matlab 的Simulink 模块对该船的运动与控制进行了数值仿真[50]，并通过模型试验进行了验证[51]。2002 年，Giron-Sierra 等[52]引入滤波算法和时变松弛法（Time Variant Relax，TVR），对传统的PD 控制进行了改进。计算结果表明，控制附体除了减小晕船率（Motion Sickness Incidence,MSI）之外，还应该考虑其他优化目标，例如减少船体振动和执行器的操作频率、避免空化。同年，该团队通过遗传算法对控制策略进行了多目标优化[53]。2003 年，Giron-Sierra 等[54]采用完全面向控制的模型（Control-oriented model）研究了高速船的PID 控制问题，结果表明，主动控制附体对波浪中船舶航态的稳定有重要作用。随后，Esteban 等[55]改进了该垂向运动的控制模型，计算结果表明，引入主动控制的减摇附体后，船舶在高速高海况下的垂向加速度可降低65%，晕船率可减小35%。与此同时，Sclavounos 等[56]采用三维Rankine 面元法研究了高速单体船的耐波性，计算发现，安装于艏部的水翼可减少不规则波中（Jonswap 谱）多达50%的垂荡和纵摇运动。

2001 年，Aranda 等[57]采用了不同的附体控制策略（包括传统PID 控制和采用遗传算法进行优化）来降低高速单体船的晕船率。结果表明，在高海况时波浪引起的垂向加速度更高，并且由于需要提供更大的恢复力（矩）来对抗垂向波浪力，附体的减摇效果有所降低。随后在2005 年，又研究了使用多变量鲁棒控制器来降低船舶航行时的晕船率[58]。Díaz 等[59-60]利用定量反馈理论（Quantitative Feedback Theory, QFT）设计了一种单变量的鲁棒控制器，可以有效减少高速船的垂向运动和晕船率。此外，De La Cruz 等[61]使用模糊控制理论，在不同的航速和海况下较大限度地改善了船舶的耐波性。López 等[62-63]将神经模糊控制系统推广到了对T 型翼和艉压浪板的控制中，规则波和不规则波中附体减摇的仿真结果表明，该控制策略可以降低晕船率，并对船舶运动起到良好的预测作用。总之，Giron-Sierra 等[64-68]开展的附体控制策略和多目标优化研究大大改善了高速单体渡轮的耐波性并且降低了晕船率，与传统PID控制相比，解决了船舶纵向运动系统的非线性以及实际海洋条件下的干扰问题。但是，其闭环控制系统也存在控制精度低、动态调节能力差的缺点。而基于传统PID 算法的控制器以其结构简单、参数容易整定等一系列优点，依然在实际船舶减摇系统中得到了广泛应用。

Xi 等[69]研究了采用压浪板的减摇控制系统。首先以固定角度研究了其开环运动特性，然后采用线性控制器，解决了非线性系统结构复杂、干扰因素多的问题。2011 年，Hughes 等[70]采用大振幅运动程序（Large Amplitude Motion Program, LAMP）针对某高速穿浪双体船开发了基于PID 控制的航态控制系统。该系统基于时域势流理论求解三维波浪对船体的水动力和刚体动力问题，并通过与模型试验结果对比验证了方法的有效性。研究结果表明，T 型翼和艉板的主动控制对船舶纵摇和横摇运动有明显的减摇效果。

1.3.2 国内研究进展

我国对于船舶运动控制策略的研究始于20 世纪90 年代，以传统PID 控制为主。2002 年，金鸿章等[71-72]提出了变参数PID 控制器，并进行了减摇鳍控制的计算机仿真，结果表明，当船舶自然横摇周期和无因次横摇衰减系数变化时，在各种浪向下，具有变参数最优PID 控制器的减摇鳍都有很好的减摇效果。席裕庚等[73]提出了一种非线性系统预测控制算法并证明了它的有效性。由于船舶在海上的运动具有时变性，采用预测控制可在一定程度上克服系统不确定性的影响。

近年来，预测控制已被应用于船舶纵向运动姿态控制系统的设计中。2015 年，窦静怡[74]对模糊PID 和广义预测控制这2 种算法的减摇效果进行了对比，计算结果表明，改进的预测控制算法对高速双体船纵向运动具有理想的减摇效果。高海况下，垂荡和纵摇减摇百分比可达40%～60%，艏加速度减少约60%，比模糊PID 控制的减摇能力提升7%～17%。2017 年，张伟[75]对有输入约束的双体船纵向运动控制系统设计了模型预测控制器，计算结果表明，相比裸船模，采用主动T 型翼的双体船可减少垂荡位移60%以上。2018 年，刘娜[76]将T 型翼和艉压浪板作为多体船的减摇附体，采用ANSYS 计算高速多体船的水动力系数，选用传统PD 控制和模糊控制作为附体控制方法，对高速多体船的垂荡和纵摇情况进行了仿真计算，证明了在引入模糊控制后减摇效果可提升15%左右，并得到了T 型翼和压浪板的最优结构布局。2018 年，刘志林等[77]针对某三体船利用CFD 计算三体船的水动力系数，采用预测控制的方式以晕船率函数为优化指标，对比研究了无T 型翼的裸船模和引入主动控制的T 型翼在波浪中的垂荡和纵摇以及其对晕船率的影响，验证了预测控制的有效性，取得了纵摇角最多减少59.34%的效果。在此基础上，刘志林等[78]进一步提出了基于预测控制算法的鲁棒容错控制算法，考虑到模型的鲁棒性、传感器可能发生的故障以及T 型翼攻角的输入约束，改进了对T 型翼的控制，并将此方法应用到了双体船的减摇中[79]。

除了基于PID 控制理论的控制方法外，为了保证控制系统具有较强的鲁棒性，张显库[80]采用多进多出(Multiple In Multiple Out，MIMO)闭环增益成形算法设计了鲁棒控制器，给出了水翼艇纵向运动传递函数形式的数学模型，通过镜像映射方法将不稳定模型转换成稳定的数学模型，计算结果表明，纵摇角降低了25%。在此基础上，张显库[81]引入正弦函数驱动的非线性反馈代替原有的误差线性反馈，与单纯的鲁棒控制器相比，垂荡的减摇效果提升达70%以上。刘维亭等[82]提出了鲁棒控制在船舶减摇鳍控制中的应用，在不同海况下均取得了较好的控制效果。常进[83]利用2.5D 理论对某穿浪双体船进行水动力计算，应用鲁棒控制理论中的μ综合设计思想对T 型翼减摇系统进行设计，采用Matlab 平台对控制器设计中的D-K 迭代进行计算并对系统权函数进行了改进，对未来应用鲁棒控制中权函数的选择具有一定的启发意义。

刘金玲[84]、张松涛等[85]采用2.5D 理论求解船舶运动的水动力系数，以90 m 的穿浪双体船为例，分别利用线性二次型调节器(Linear Quadratic Regulator，LQR)和状态反馈H∞控制算法作为控制器，建立仿真模型，验证了这2 种姿态控制器均可减小船舶纵向运动，改善船舶的性能，并且状态反馈H∞控制器的减摇效果更好，垂荡位移可减少20%，纵摇角可减摇43%。原新等[86-87]以某高速三体船为研究对象，采用AQWA 和CFD 建立带T 型翼的三体船纵向运动模型，对比了采用滑模变结构和LQR 这2 种控制器控制T 型翼后对三体船运动的减摇效果。计算结果表明，由于滑模变结构控制器具有非线性、不连续的特点，其减摇效果要略好于LQR 控制器，可减小垂荡运动25.1%、纵摇41.3%。

2 试验研究

2.1 国外研究进展

关于采用减摇附体对船舶纵向运动进行抑制的试验研究，Esteban 等[13]针对某单体高速渡轮进行了水池试验研究，安装了T 型翼和艉压浪板，首先测量了不同攻角下附体的垂向力（矩），并通过CFD 程序计算船的水动力系数，然后设计了针对晕船率、空化现象以及机械效率的多目标优化PID 控制程序，摆角控制信号选择的是纵摇角和纵摇角速度联合控制，最后测量了裸船模和加装含主动控制程序的附体后模型在20，30 和40 kn航速下的加速度和晕船率。试验结果表明，40 kn航速下主动控制程序最多可减少晕船率47.67%，晕船率较被动控制条件下降低了约28%。

Rijkens 等[88]对一尖舭单体船安装了基于PID控制的艉压浪板和扰流板，结果表明，艉压浪板改善了船的水动力性能，主动控制的艉压浪板使加速度减小了25%。2013 年，他们设计了新型减摇附体，一种可提供正负两个方向升力的扰流板，扰流板与船艉封板底部之间有一个倒圆角，计算结果表明，扰流板可有效减少垂向加速度，峰值处可减少40%[89]。

穿浪双体船由于具有细长的侧体，高速航行时比单体船更容易产生剧烈的垂向运动[90-92]。2009 年，Lavroff 等[93-95]对某2.5 m 双体船水弹性分段模型进行了拖曳水池试验，测量了其在规则波中的砰击力，并将艉压浪板（被动控制摆角为0°）安装于船艉，但是艏部并没有安装T 型翼。在随后的研究中，Davis[96]和Jacobi[97-98]等在先前对一艘86 m 高速双体船进行运动响应测试的基础上，开展了实船和模型试验研究。对该穿浪双体船引入了航态控制系统，针对船体结构应力变化率随船体纵摇运动的变化规律，实现了通过海况和船模运动预报砰击运动，研究了该航态控制系统对砰击发生率的影响，结果表明，减小船舶的垂向运动可以明显改善砰击发生率。

Alavimehr 等[99]利用循环水洞测量了一种低展弦比、水平翼翼展边缘较尖的T 型翼在静态和动态这2 种情况下不同攻角对应的升力，并与机翼理论、Theodorsen 振动翼理论进行了对比。试验结果表明：由于水平翼的升力受到其表面附近其他构件（垂直翼、连接件等）的影响，实测的升力系数要比理论值偏低；并且在T 型翼摆角转动角速度较高时，采用Theodorsen 理论计算升力系数要略好于静态机翼理论。该试验同时也表明，低雷诺数的T 型翼在较低展弦比下的非定常性能足以满足拖曳水池试验的要求。在此基础上，在静水中进行了航态控制系统的开环控制研究[100]，利用T 型翼和艉压浪板连续转动产生的垂向力引起船模运动，通过试验确定了只让模型产生垂荡（纵摇角接近0°）或者纵摇（垂荡接近0 mm）运动的T 型翼和压浪板摆角的组合，为航态控制系统的进一步完善奠定了基础。最后，规则波中的模型试验验证了该系统的减摇效果，试验结果表明，在波高较高的工况下（规则波波高90 mm），纵摇响应最多可降低60%，砰击压力最多可降低75%[101]。

2.2 国内研究进展

国内关于高性能船减摇的试验研究，早期的主动控制是以正弦信号控制附体转动。1997 年，丁勇等[102]在单体船模上加装了不同尺度的艏鳍、船艏椭圆环形翼、纵列片翼，并对比了引入以正弦信号主动控制片翼后（翼摆角范围为−22°～22°）模型的纵摇运动。试验结果表明，引入主动控制后，5 级海况下纵摇幅值可减少25%～30%。之后，Jiao 等[103]进行了大量的水池试验、海上试验和理论研究，采用被动控制鳍和半潜艏来改善高速船的耐波性。试验结果表明，两种附体均对减小模型的纵摇和艏加速度有很好的效果。

2002 年，Lin 等[104]研究了采用可控艉压浪板设计来减小圆舭船在波浪中的垂向运动，并通过试验进行了验证，在此基础上选用可振动艉压浪板代替可控艉板，测量了其对纵摇运动的减摇效果。模型试验表明：如果能在波浪扰动和艉板恢复力之间建立合适的相位，使用振动翼可以很好地减小纵摇运动。

关于T 型翼的模型试验，郑义和董文才[105]对高速轻型穿浪双体船的纵向运动减摇进行了理论和试验研究，分析了水翼的尺度、形式、安装位置对纵向运动的影响，发现纵摇和垂荡运动有义值可减少20%～30%。梁洪光[29]对加装T 型翼的三体船进行了不同航速和不同波长规则波中的运动试验，结果表明，高速时（傅汝德数Fr=0.509）被动式T 型翼最多可以减少艏加速度24%，而减摇效果则会随着波长的增加而减小。闫蕾[106]研究了攻角固定的T 型翼对三体船型运动性能的影响。结果表明，在规则波中，相对于常规后三体船型，带T 型翼的前三体船型的迎浪纵向运动都得到了一定的改善。周广利等[107]对三体船加装T 型翼的阻力变化进行了试验和数值研究，通过对比3 种纵向安装位置、2 种垂直翼高度和3 种攻角情况，确定了安装T 型翼的较佳位置。

Jia 等[108-109]通过模型试验证明，在高速时侧体位于船舯前的前三体船比后三体船具有更好的阻力性能，但是耐波性在多数工况下不如后三体船。Zong 等[110]为该前三体船安装了可以随船舶运动实时改变攻角的主动控制T 型翼，采用纵摇角速度信号作为输入值对T 型翼的摆角进行实时控制，提出了T 型翼摆角的控制方程并计算了控制增益系数。规则波试验结果表明，T 型翼可减少响应峰值区域的垂荡运动约50%，较被动控制的T 型翼提高了近20%，对纵摇和艏加速度的减摇效果约为45%，比被动控制提高了约15%。在此基础上，Zong 等[111]对不规则波中2 种海况下（4 级和5 级海况）4 种不同侧体分布位置的三体船（侧体位于舯后、船舯和舯前，后三体船2 种侧体间距）进行了T 型翼减摇试验。试验结果表明：低速高海况下三体船纵向运动响应很剧烈，需要引入减摇系统；侧体分布位置对T 型翼的减摇效果影响很大，高速高海况时，T 型翼对侧体位于船舯的构型具有最为明显的垂荡减摇效果，而前三体船加装T 型翼后的纵摇和艏加速度运动减少最为明显；T 型翼摆角的控制策略可以应用于实船T 型翼设计，基于试验结果可以针对不同海况采用不同的T 型翼摆角控制策略；高速高海况下，加装主动T 型翼的前三体船具有较好的耐波性，若是选用后三体船，侧体更小的间距则在设计中更为推荐。

3 结 论

本文主要针对高性能船在波浪上纵向运动减摇的计算方法、附体控制策略以及数值和试验的相关研究进行了详细综述，分析了研究进展。目前，对于纵向运动的减摇附体以T 型翼为主，在船的艉部辅以艉扰流板或压浪板来降低阻力并增加恢复力矩，继而提高减摇效果。

针对船舶运动的计算方法以基于理想流体的势流理论和基于黏性流体的CFD 方法为主。势流理论部分的计算方法主要包括切片理论以及由此发展而来的2.5D 理论。2.5D 理论因其可以有效解决高速船舶运动的强非线性动力问题而在近年的研究中得到了广泛应用。在此基础上，将离散涡法引入该理论形成的自由表面随机涡法，用离散涡法模拟流体的黏性，采用无网格降阶模型，在保证计算精度的同时具有很高的计算效率，该方法对于船舶运动的预报有着很广阔的研究前景。而CFD 方法的优势在于对黏性流体中船舶及附体附近流场的模拟，并且随着计算机技术的进步，CFD 方法对船舶运动的计算精度和计算效率也随之提高，因而已被大量用于船舶减摇系统的设计中。

关于附体运动控制信号的研究，主要是采用纵摇或垂荡运动作为输入信号进行控制。结果表明：采用纵摇角速度信号对模型的纵摇角减摇比较明显，而对垂荡的效果较差；而采用垂荡速度信号作为输入则可以较好抑制附体的垂荡运动，但是对角位移的限制不理想。因为模型的艏部加速度受纵摇运动影响较为明显，所以现有的控制方式多以纵摇角速度信号作为输入。但由于垂荡信号同样具有减小垂荡位移好的优势，因此，如何将两种信号进行融合继而改进控制系统是未来的研究方向之一。

减摇控制方法方面，理论研究在早期的传统PID 基础上引进了模糊控制和神经网络方法对控制参数进行整定，改进了传统方法不能及时根据海况调整控制参数的缺点，获得了更好的减摇效果。滑膜变结构控制以及鲁棒控制中的结构奇异值理论和H∞理论也被应用到运动控制系统的设计中，减摇效果比传统PID 方法有了明显提升；计算结果表明，采用滑模变结构控制和H∞理论的减摇效果要略优于LQR 控制。此外，广义预测控制方法的减摇效果较之PID 方法有明显提升，且计算相对简单，稳定性好，未来有较好的应用价值。由于传统PID 控制具有结构简单、参数容易整定等优点，所以对于附体主动控制减摇的模型试验研究主要还是采用PID 控制为主，今后的研究主要是将其他控制策略应用于实际试验，以提高减摇附体对船舶纵向运动的减摇能力。