小波-ARIMA模型在贵广高铁隧道沉降预测中的应用
2020-06-02毕旋旋邓开元于志文
毕旋旋,任 超,邓开元,于志文
(桂林理工大学 a.测绘地理信息学院;b.广西空间信息与测绘重点实验室,广西 桂林 541006)
0 引 言
沉降预测是隧道变形监测的重要环节之一。 通过对已有沉降数据进行数据挖掘,可以把握沉降序列的变化规律,了解变形特征,以此为施工和运营提供参考依据和信息保障。 如何利用收集到的数据进行统计分析,研究隧道变形规律并进行准确的趋势预测已成为一个研究重点,并会对隧道工程的相关研究产生重大意义[1-2]。 由于诸多随机性因素的影响,沉降数据表现出非线性和时变性的特征,从而让准确的沉降预测变得十分困难。目前,国内外关于沉降预测的研究已较为深入,并产生了较多的预测方法,如BP神经网络、支持向量机(SVM)、自回归移动平均模型(ARIMA)等。BP神经网络学习算法过分强调克服学习错误而泛化能力不强,同时,采用BP神经网络进行非线性拟合预测,当训练样本不足或质量不佳时,会出现陷入局部极值、过度拟合和结构设计盲目等问题[3]。而SVM避免了过度拟合的出现,很大程度地增加了全局寻优的能力,适合小样本的快速预测; 然而,SVM也存在一定的局限性,对复杂的非线性、季节性和长期性数据的预测精度会有所下降[4]。 ARIMA考虑到监测数据对时间序列的依赖性,对于小样本预测精度较高,可以将非平稳时间序列转换为平稳时间序列,是对非平稳时间序列进行预报的一种常用方法[5], 但ARIMA对数据质量要求较高,建模选取参数较为困难。 而小波分析对数据具有良好的局部化特性,可以提取数据的任何细节,能更好获取有用信息,改善数据质量。
基于此,本文提出一种基于小波分析(wavelet analysis)的ARIMA算法。 使用小波对原始序列进行分解、重构,然后对重构序列的趋势项和随机项分别构建ARIMA参数并进行预测,最终叠合预测结果以实现对隧道沉降的预测。
1 基本理论
1.1 小波分析理论与Mallat算法

(1)
则可称Ψ(t)为基本小波(母小波)。Ψ(t)通过尺度伸缩和平移生成函数族
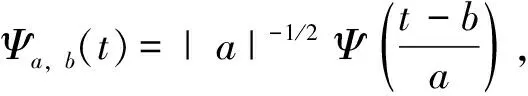
(2)
式中:a是伸缩参量,b是平移参量(a,b∈R),a≠0。a、b取连续变量时,Ψa,b(t)即为依赖a、b的连续小波函数[6-8]。本文采用的分析方法是基于Mallat算法支持的小波对沉降序列的分解与重构。Mallat算法是对小波变换的一种改进,是小波变换的快速实现算法,核心是引入多分辨率分析的思想[9]。
1.2 ARIMA模型
自回归移动平均模型(ARIMA)是一个可以衡量内生变量与其滞后性与改变量关系的一个系统模型,是对移动平均模型(ARMA)的扩展[10-11]。ARIMA(p,d,q)的实质是ARMA(p,q) 的d阶单整(d次差分),该效果将一个非平稳的时间序列转化为平稳时间序列。将隧道沉降序列yt进行差分
ut=Δdyt=(1-B)dyt,
(3)
式中:B为后移算子,u为差分算子。 在经过d次差分后变为平稳序列,即可建立ARIMA(p,d,q)模型的一般形式:
ut=Φ1(yt-1-yt-2)+Φ2(yt-2-yt-3)+…+Φp·
(xt-p-xt-p-1)+εt-θ1εt-1-θ2εt-2-…-θqεt-qΦ1(ut-1)+Φ2(ut-2)+…+Φput-p+
εt-θ1εt-1-θ2εt-2-…-θqεt-q,
(4)
式中:Φ为自回归系数;p为自回归阶次;q为滑动平均阶次;εt是白噪声序列。
1.3 小波-ARIMA建模流程
小波-ARIMA(下文称W-ARIMA)模型的优势在于,将经过小波分解的序列转化为一个概貌序列和一个细节序列,且分解后有良好的平稳性和平滑性。因此,对于一些非平稳时间序列,经过小波分解后便可以使用传统的时间序列方法建模预测。在对沉降序列采用小波分解后,对不同特征的波形可以选择不同的p、d、q参数,以最优方式进行拟合预测[12]。本文结合模型自身特点,按照如下步骤进行建模:1)利用Mallat算法小波对沉降序列进行分解与重构,得到低频分量A1与高频分量D1,同时考虑多层分解的可能性;2)引入ADF单位根检验法以检验序列的平稳性,在序列不满足平稳性条件时,通过d次差分变换使得序列满足平稳性条件; 3)计算序列的自相关系数(ACF)和偏相关系数(PACF),对模型进行初步识别; 4)通过赤池信息准则(AIC)和SBC准则来确定最优模型参数;5)估计模型未知数,并通过参数的t统计量检验其显著性以及模型合理性;6)对沉降序列进行预测,并检验残差序列是否为白噪声序列,若不满足,返回步骤3); 若满足,则通过; 7)利用所构建的模型对序列进行拟合和预测,并叠加得到最终预测结果。
W-ARIMA模型的建模流程如图1所示。

图1 W-ARIMA隧道沉降建模流程Fig.1 Modelling process of W-ARIMA tunnel subsidence
2 实验分析
2.1 数据准备
以贵广高铁桂林-恭城路段某隧道断面为例,并展示断面DK 0520+441的建模预测过程。该隧道穿越山体,地形起伏较大,地表植被茂盛。坡面土层较薄,绝对高程300~1 200 m,自然坡度20°~55°,洞身主要为花岗岩,地质条件较好。此隧道的监测周期为7 d,本文选取其中2013年5月6日—2014年3月10日共45期观测数据进行分析。两断面的原始观测数据如图2所示。
2.2 ARIMA模型的构建
在进行拟合预测前,应对ARIMA模型进行定阶。本文拟对该断面沉降序列前35期数据进行ARIMA建模,预测后10期数据。首先,对建模数据进行小波分解,文献[13-14]指出,db小波能够较好地分解沉降数据非平稳信号,所以本文拟采用db4小波基函数对建模数据进行分解,同时文献[15]中指出由于预测结果是对小波分解所得系数序列的预测结果进行重构而获得,为避免重构过程中预测误差的累积,本文拟采用一次分解即可满足实验要求。对前35期原始数据进行小波分解,将高频系数序列与低频系数序列绘成图3。分别对子序列进行ARIMA建模分析,以数据高频分量为例,进行模型构建分析。先引入ADF单位根检验法,判断序列平稳性[14]。ADF检验模型为(c,t,2),ADF检验结果见表1。

图2 隧道断面原始观测数据Fig.2 Original observation data of tunnel section
可知,该序列能够满足ADF在1%检验水平下的临界值,故可以认为其平稳,选择零次差分,d取0。为确定p、q值,此处作出该高频序列滞后16阶的ACF、PACF(图4)。

图3 小波分解的DK 0520+441隧道断面观测数据Fig.3 Observation data of DK 0520+441 tunnel section by wavelet transform

表1 序列ADF检验结果Table 1 ADF test results

图4 隧道沉降序列ACF、PACF函数Fig.4 ACF and PACF test functions of tunnel settlement sequence
分析可知,ACF函数与PACF函数均表现出拖尾性。ACF函数2步截尾,PACF函数3步截尾。根据ARMA(p,q)模型识别原则,可以分别对p、q初步定阶。为获取p、q确定值,引入赤池信息量准则(AIC),选择初步定阶参数一定邻域内整数进行验证,满足AIC最小原则时,可以确定p=2、q=3。因此可以对序列高频分量构建ARIMA(2,0,3)模型,并以此进行回归,再进行残差白噪声检验,由残差的ACF、PACF函数(图5)可知,残差为白噪声序列,平均值接近于0,服从零均值,故可认为该模型可靠。同理,对其他序列构建ARIMA模型。
2.3 模型的预测
依据2.2节定阶的ARIMA模型,分别对小波分解的序列进行建模预测,得到高频序列与低频序列的预测值,再将二者的预测值重构,进而得到最终的预测值,并与直接使用ARIMA建模预测得到的预测值进行比对分析,二者精度详见表2。

图5 残差的ACF、PACF函数Fig.5 Residual of ACF and PACF
表2 各模型精度评定
Table 2 Precision comparison of all models mm

期数实测值ARIMA模型预测值残差相对误差/%W-ARIMA模型预测值残差相对误差/%361.401.48-0.085.701.48-0.085.70 371.281.43-0.1511.701.35-0.075.50 381.251.31-0.064.801.29-0.043.20 391.301.280.021.501.260.043.00 401.381.330.053.601.39-0.010.70 411.341.41-0.075.201.37-0.032.20 421.341.37-0.032.201.38-0.042.90 431.361.41-0.053.701.40-0.042.90 441.311.39-0.086.101.34-0.032.20 451.341.41-0.075.201.37-0.032.20
同时,为更好地评定二者的预测精度,本文引入精度指标均方根误差(RMSE)、平均绝对误差(MAE)、平均相对误差(MRE)和相对误差δ
(5)
(6)
(7)
(8)

表3 模型计算结果对比
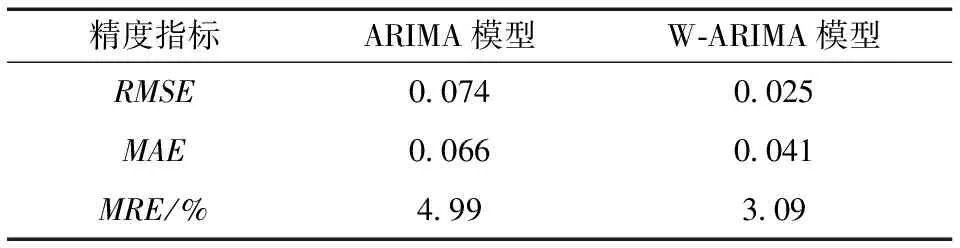
Table 3 Calculation results comparison of all models mm

图6 模型计算结果对比Fig.6 Calculation results comparison of all models
综合可见,改进模型捕捉了高、低频率分离的波形特征,进行了具有针对性的建模,完善了原模型的预测性能。虽然极个别期数发生了改进模型失稳,预测精度低于原模型的情况,但占比极低,就整体而言,改进模型精度(RMSE)提高了66.2%。
3 结 论
本文利用ARIMA和W-ARIMA模型对高铁隧道沉降数据进行建模分析,探讨了其在高铁隧道沉降监测中的应用,结合贵广高铁隧道沉降监测数据,对两种方法进行了比较分析。 得出以下结论:
(1)无异常波动情况下,两模型均有较好的拟合精度,MRE均不超过5%。
(2)沉降序列发生较大波动时,W-ARIMA的预测曲线稳定性更强,此时ARIMA模型虽能保持一定的沉降曲线趋势,但预测精度发生明显下降。
(3)在实际高铁隧道断面监测工作中,W-ARIMA模型可以较好地预测沉降趋势,为安全施工和运行提供参考依据。
