一种基于超限稀疏多项逻辑回归和奇异谱分析的高光谱遥感影像分类方法

何艳萍,陈天伟,郑旭东,沈宇臻

(桂林理工大学 a.测绘地理信息学院;b.广西空间信息与测绘重点实验室,广西 桂林 541006)

0 引 言

高光谱遥感影像分类是高光谱遥感影像实际应用中的重要组成部分,同时也是技术难点之一。目前,国内外学者对高光谱遥感影像分类进行了大量研究,但分类算法有效性、分类方法稳定性等仍亟待提高。虽然高光谱图像(hyperspectral image,HSI)中可用的丰富光谱信息使得在相似的材料物质之间进行分类成为可能[1],但是由于训练样本的缺乏及高光谱影像的多维性[2],使得高光谱图像分类精度相对较低。 为了解决上述问题,众多算法被研究应用于高光谱遥感影像分类,如: 多核分类(multi-kernel classification,MKC)、支持向量机(support vector machine,SVM)、低秩表示(low-rank representation,LRR)、极限学习机(extreme learning machine,ELM)及稀疏多项逻辑回归(sparse multinomial logistic regression,SMLR)[3-8]等。 此外,在针对高光谱遥感影像的多维特征时,也诞生了许多用于降维和特征提取的方法,主要包括分段自动编码器(segmented stacked auto-encoder,SSAE) 及线性判决分析(linear discriminate analysis,LDA)[9-10]等。在上述方法中,稀疏多项逻辑回归因其良好的稳定性和有效性,取得了较为广泛的应用[11-12]。但由于稀疏多项式逻辑回归在处理高维度的特征时仅利用原始的光谱信息,不具备良好的特征投影性能,且其初始回归值需要人工设定,使得其在针对高光谱遥感影像分类时具有较大的局限性。为了解决这两个缺点,文献[8]提出了一种超限稀疏多项逻辑回归(extreme sparse multinomial logistic regression,ESMLR)算法。超限稀疏多项逻辑回归可以将高光谱数据集投射到具有随机生成的权重和偏差的新特征空间且通过拉格朗日乘数法和对偶原理建立的优化模型,再通过最小化训练误差和自动确定回归量的条件为稀疏多项逻辑回归得到一个良好的初始回归量。因此，超限稀疏多项逻辑回归在针对高光谱遥感影像分类中相比于稀疏多项式逻辑回归更具适用性。

但在高光谱影像中,由于受影像成像时周围环境和传感器本身的影响,使得影像存在较多的“同物异谱、同谱异物”的现象,进一步增加了分类的难度[13]。 传统的超限稀疏多项逻辑回归算法不具备良好的图像内在结构分析性能,且由于超限稀疏多项逻辑回归在处理数据方面仅对影像进行了特征投影变换,故也不具备内在特征分析性能,从而使该算法在针对具有多维、海量数据特征的高光谱遥感影像分类时,还存在一定的不足。

为了解决上述问题,本文提出了一种基于超限稀疏多项逻辑回归和奇异谱分析(singular spectrum analysis,SSA)的高光谱遥感影像分类方法。奇异谱分析是一种时间序列分析和预测技术[14],其主要目标是将原始系列分解为若干独立子系列[15]。这些子系列是可解释的,即它们可以主要被识别为变化的趋势——振荡或噪声。奇异谱分析的主要功能可归纳为[15-16]:1)分析复杂的趋势和不同幅度的周期; 2)对信号的趋势、周期性成分进行提取和平滑; 3)对振荡信号的包络分析。因此,结合超限稀疏多项逻辑回归和奇异谱分析将会进一步提高超限稀疏多项逻辑回归用于高光谱图像分类的精度。本文方法首先利用奇异谱分析对归一化处理后的高光谱遥感影像数据原始系列分解为若干独立的子系列,然后进行重构,以达到去除噪声信息及提取有效信息的目的,随后联合具有良好性能的超限稀疏多项逻辑回归算法实现对高光谱遥感影像分类。

1 超限稀疏多项逻辑回归

设定有n个训练样本x=[x1,x2,…,xn]∈Rd×n和相应的标签Y=[y1,y2,…,yn]∈RM×n,其中d为高光谱图像的层数,M为高光谱图像的总类别个数。超限稀疏多项逻辑回归用于高光谱图像分类建模[8]:

(1)

(2)

其中,h(xi)是多项逻辑回归的输入特征且h(xi)=[xi1,…,xid]T,w=[w(1),…,w(M-1)]T∈R(M-1)×d表示回归量。由于式(1)、(2)的密度不依赖于回归量的平移,所以wM设置为0[7]。

可通过优化以下方案来解决稀疏多项式逻辑回归的初始回归值问题。

Minimize‖wH-Y‖2and ‖w‖2,

(3)

其中,Y=[y1,y2,…,yn]∈R(M-1)×N;

(4)

其中:C为正则化参数;ξi为样本的训练误差。

基于Karush Kuhn Tucker最优性条件和拉格朗日乘子法[16],可得

(5)

其中,aij为拉格朗日乘子。

因此,通过解决式(5)可得超限稀疏多项逻辑回归的初始回归值为

(6)

基于超限稀疏多项逻辑回归的算法原理,在第k次迭代中提出的超限稀疏多项逻辑回归的回归量w可以通过最大后验估计来计算

(7)

其中,p(wk-1)∝exp(-λ‖wk-1‖1)和λ是用于控制稀疏度的正则化参数,k=1,2,…,n。

2 本文方法

假设一个高光谱图像像素点X=[X1,X2,…,XN]∈RN的向量阵列x中有1个一维信号,首先将高光谱图像数据归一化,然后采用奇异谱分析对数据进行处理。奇异谱分析算法可分为嵌入、奇异值分解、分组及对角平均和投影4部分。

2.1 嵌入

定义一个窗口大小L∈Z满足L∈(1,N),矢量x的轨迹矩阵X可以被表示为[14]

(8)

式中:X,CK的每一列是一个滞后向量,可以表示为CK=[XK,XK+1,…XK+L-1]T∈RL,其中k∈[1,K],而K=N-L+1。值得注意的是沿着矩阵X的反对角线有相同的值。因此,其实质上为一个汉克尔矩阵[15]。

2.2 奇异值分解

首先,由轨迹矩阵X可得到矩阵S，因为S=XXT,S的特征值及其各自对应的特征向量可分别用(λ1≥λ2≥…≥λL)和(U1,U2,…,UL)表示。对于轨迹矩阵X,令d等于X的秩,为简便,可令d=L。例如:

X=X1+X2+…+Xd。

(9)

可以看出,轨迹矩阵X实际上是由几个矩阵相加得到。每个矩阵Xi|i∈[1,L]称为初等矩阵,对应于其各自的特征值被下式所定义

(10)

其中,Vi被定义为

(11)

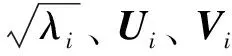
U=(U1,U2,…,UL)∈RL×L,

V=(V1,V2,…,VL)∈RL×L。

(12)

2.3 分组

在此步骤中,L分量的总集合被分为M个不相交的集合,I1,I2,…,IM,其中∑|Im|=L,而m∈[1,M]。设I=[i1,i2,…,ip]表示分割组中的一个,与组I相关的矩阵XI被定义为XI=Xi1+Xi2+…+Xip。最后,轨迹矩阵X被表示为

X=XI1+XI2+…+XIm。

(13)

为简单起见,典型的分组是m=L,即p=1,并且为了方便,本文中只考虑p=1的情况。这是指每个集合仅由一个部分组成的情况。一般来说,每个矩阵XI对SVD中的轨迹矩阵X的贡献与其特征值紧密相关,因此可以得到[12]

(14)

2.4 对角平均和投影

通过之前的分组获得的矩阵XIm(m∈[1,M])不一定为原始轨迹矩阵中的汉克尔矩阵类型。但是,为了将这些矩阵投影至一维信号,需对其进行约束，可以通过获得XIm的所有反对角线的平均值来实现,因为这些用于平均值的值对导出的一维向量阵列中的相同元素贡献一致。

设Zm=[Zm1,Zm2,…,Zmn]∈RN表示从XIm投射的一维信号,其可通过对角线平均获得,即

(15)

其中：j,n-j+1指的是XIm的元素,由此得到Zm。最后原始的一维信号可以被重建为

(16)

(17)

训练完成则可用剩余样本或者整个高光谱数据集进行分类测试

(18)

3 实验部分

3.1 实验数据

采用Indian Pines[8]和Pavia University[19]标准数据集对本文方法的有效性进行实验论证,Indian Pines数据集由AVIRIS传感器于1992年6月拍摄,数据集大小为145×145×220,移除20个水污染的波段后,此数据集的大小为145×145×200,共有10 366个样本,16个类别,具体类别名称及各类样本数见表1。

Pavia University高光谱标准数据集为光谱成像仪ROSIS于2003年对意大利帕维亚城成像结果提取的帕维亚大学部分,空间分辨率1.3 m,数据大小为610×340×103,成像波长范围0.43～0.86 μm,数据共含有9个地物类别,具体类别名称及各类样本数见表2。

为了对比本文提出方法的有效性,本文利用ESMLR[8]、ELM[20]及ESMLR-AP进行对比论证,其中ESMLR-AP方法是利用属性剖面(attribute profile,AP)[21]代替SSA进行影像噪声处理并利用ESMLR进行分类的一种方法。训练样本数量采用每类5、10、15、20、25、30个,另外,为证明本文方法的稳定性,另取每类1%的数据作为训练样本进行实验(考虑篇幅问题,对Pavia University数据集实验中仅采用每类5、10个像元作为训练样本)。 采用总体精度(overall accuracies,OA)、平均精度(average accuracies,AA)、Kappa系数以及这3个指标的标准差对实验结果进行精度分析,为保证实验的有效性及合理性,所有训练样本都为随机抽取,且所有实验结果都为10次平均值。

表1 Indian Pines的各类样本数Table 1 Numbers of Indian Pines samples

表2 Pavia University的各类样本数Table 2 Numbers of Pavia University samples

为了测试奇异谱分析算法中参数L的大小对实验结果的影响,利用不同尺度的L对Indian Pines高光谱图像进行处理,参数分析实验中,对高光谱图像均随机选取每类30个训练样本(当数据集中的某一类样本个数不足30个,则最多采用该类别总样本数的一半),随后通过超限稀疏多项逻辑回归进行测试来分析L的大小对分类精度的影响,结果如图1所示。

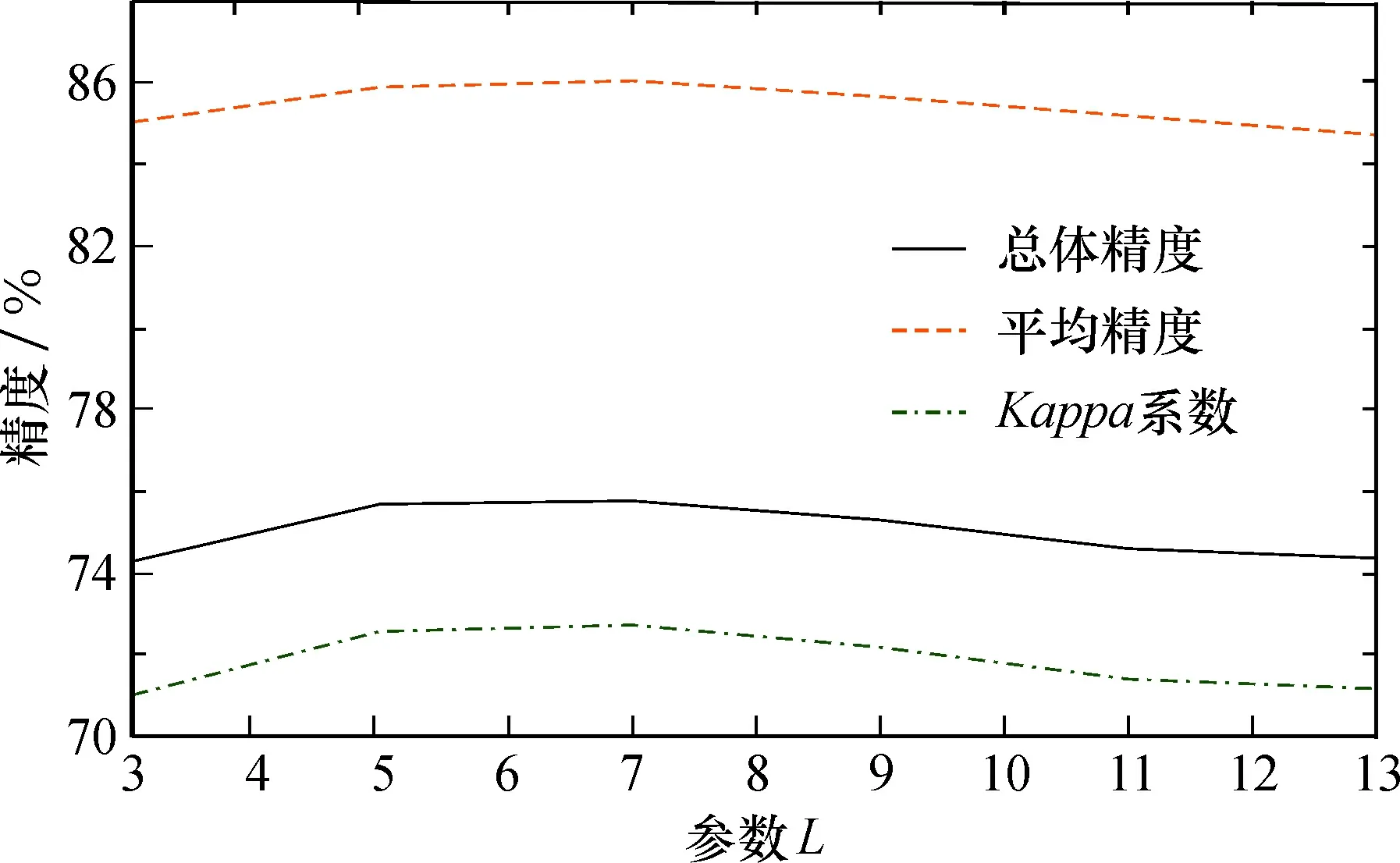
图1 参数L对分类精度的影响Fig.1 Effect of parameter L on classification accuracy

可以看出,当参数L不断增大时,分类精度增加,但是当L持续增大超过某值时,则分类精度逐渐下降。故为了实验结果最优化,使L=5。

3.2 实验结果及对比分析

采用不同个数的训练样本进行实验,设Q为高光谱数据集中每类采用的训练样本数(当某个类别样本少于Q个,则最多采用该类别样本总数的一半用作训练)。本文仅展示当训练样本为5时的各方法分类结果图,如图2所示。

表3、4分别给出了Indian Pines数据集分类实验及Pavia University数据集分类实验中ELM、ESMLR、ESMLR-AP和本文方法的分类结果数据及1%训练样本时4种算法的运行耗时可知,在对2个标准数据集进行分类所得分类精度相比于ELM、ESMLR、ESMLR-AP三种对比算法皆有较好的提高,因此,本文方法相对于ELM及ESMLR具有一定的有效性及鲁棒性,能较好地适用于高光谱遥感影像的分类。

4 结 论

超限稀疏多项逻辑回归虽然解决了稀疏多项逻辑回归存在的两个问题,具有良好的特征投影功能和通过解决一个凸优化问题可以设置良好的初始回归值,但超限稀疏多项逻辑回归不具备分析高光谱图像内在结构的功能。由于高光谱影像存在大量的噪声,为了解决超限稀疏多项逻辑回归这个缺陷,以提高影像分类精度。本文提出了一种基于超限稀疏多项逻辑回归和奇异谱分析的高光谱遥感影像分类方法,实验结果证明,本文方法相对于ELM、ESMLR、ESMLR-AP三种常用算法具有一定的有效性和鲁棒性。

图2 不同算法下每类取5个训练样本下的分类效果Fig.2 Classification results of different algorithms from five training samples of each class with different algorithms

表3 在Indian Pines数据集中不同训练样本数下各算法分类结果Table 3 Classification results of different algorithms from different training samples in Indian Pines dataset

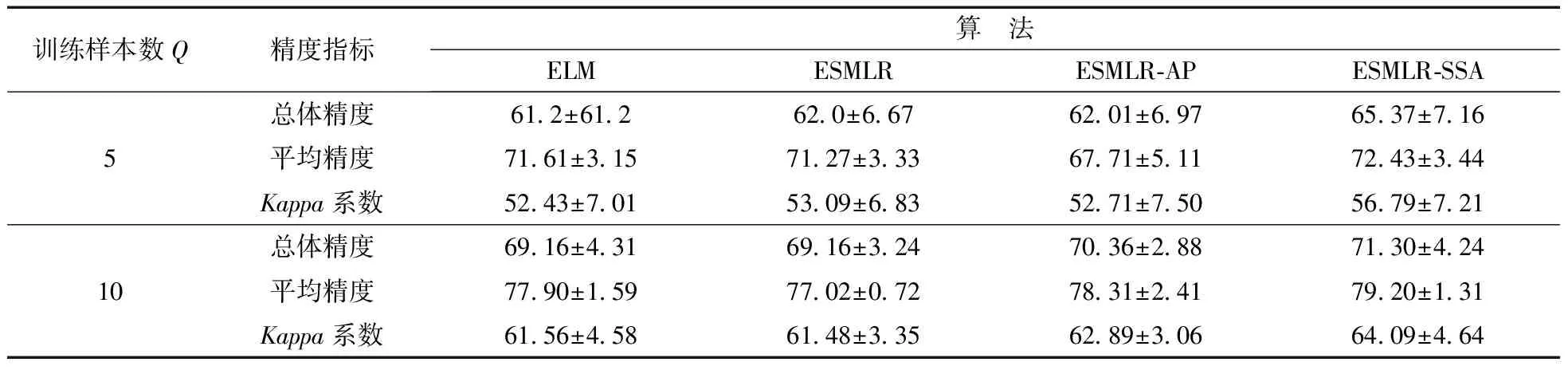
表4 在Pavia University数据集中不同训练样本数下各算法分类结果Table 4 Classification results of different algorithms from different training samples in Pavia Univerisity dataset

在以后的研究工作中,将致力于通过引入高光谱图像的坐标信息进一步提高超限稀疏多项逻辑回归在高光谱图像当中的分类结果。此外,将通过对奇异谱分析进行理论优化,如引入图论、低秩表示来减少其损耗的时间。