双变量耦合模型在水文预报中的应用

禹佳奇 包为民 包沐曦 卢金利 落全富

(1.河海大学 水文水资源学院， 南京 210098；2.南京海事局， 南京 210019； 3.浙江省台州市水文站， 浙江 台州 318001；4.青山水库管理处， 杭州 311305)

用水力学模型进行河道洪水演算，尤其是在平原河网流域效果较好[4].

上述研究都局限在有稳定水位流量关系线的河段，对于流量关系线不稳定的或潮汐河段(不存在水位流量关系)，马斯京根流量演算方法模拟实际洪水的效果仍不理想[5-8].鉴于此，孙逸群，包为民，周俊伟，等[9]提出了双变量耦合模型，本文在此基础上，概化参数，在不改变公式结构的基础上简化模型，并在更多流域进行应用检验.一方面，解决了流量关系不稳定河段的河道水流演算问题；另一方面，由现有资料可以演算得出下游的河道断面面积，以此可以实现对下游洪水的水位预报.通过长江、黄河、珠江、金沙江、松花江等不同流域的19个河段的多场次洪水资料进行验证，将结果与马斯京根法对比，双变量耦合模型在一定程度上提高了洪水预报的精度，具有一定的实际意义.

1 模型介绍

河道水流演算旨在通过上断面的流量情况演算得出下断面的流量情况，从而做出实时的洪水预报.

1.1 双变量耦合模型

双变量耦合模型[9](下文简称双变量模型)是将水流连续方程与河段蓄量方程结合，在差分基础上构造出的水流流量Q和河道面积A的双变量耦合水流演算模型.由流量Q和过水断面面积A表达的河道一维水流的连续方程为：

由Pressimann四点隐式差分格式，得：

式中：上标i和i+1代表演算时段前和后的时间；下标j和j+1分别表示河段上断面和下断面的位置；Δt为演算时段；Δx为步长值；θ为差分时间的加权系数.

河段蓄量(W)可表示为河段长(L)与河段平均过水断面面积)的乘积；也可表示为水流传播时间(K)与平均流量的乘积，即：

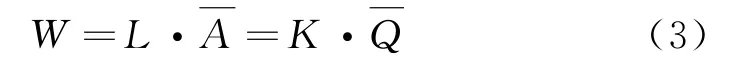
式(2)和(4)给出了一组A和Q的相互关系，解得流量演算公式如下：

式中：I为上断面流量；Q为下断面流量；AU为上断面面积.

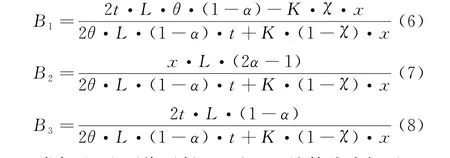
类似地，也可将下断面面积AD演算公式如下：

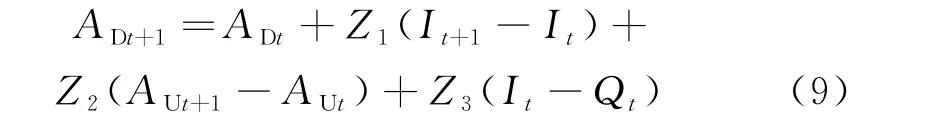
式中参数具体含义不再赘述.

将式(5)和(9)展开，参数一般化，得到如下演算公式：

式中：Bi、Zi分别为参数.

公式(5)和(9)其结构的合理性已被证明，故式(10)和(11)结构上合理有效.与原公式相比，新的演算公式隐藏了原式中具体的参数，将参数概化，在不改变公式合理性的基础上变得更简洁和实用.

1.2 马斯京根模型

马斯京根法的演算模型[10]如下：

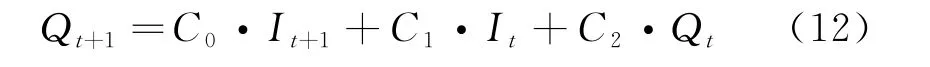
式中：Ci为参数.

2 实际流域应用

2.1 河段选择

选取河段主要考虑河段长度、流域面积以及代表性3个因素.不分段的模型演算步长为河段长，河段太长容易引起误差；减小流域面积可以降低由区间来水引起的误差；所选取的河段应尽可能包含不同情况，以检验模型的适用性.结合上述原因，根据不同的流域面积、河段长度、气候条件、断面特征等条件，选择了分布于各大水系、位于全国不同地理区域的19个河段.河段平均长度覆盖范围广，包含长江、黄河、珠江、松花江等几大流域，包括内陆河流与入海河流，以保证具有不同的气候特征、水力特征、河道特征，使其具有代表性.根据不同河段的汛期时间，选取每年汛期的洪水资料作为检验资料，选择的洪水包含了不同量级、不同历时，包含了小、中、大型洪水，历时长短从1天到几个月.选取河段的具体资料见表1，计算时间间隔采用0.5h.

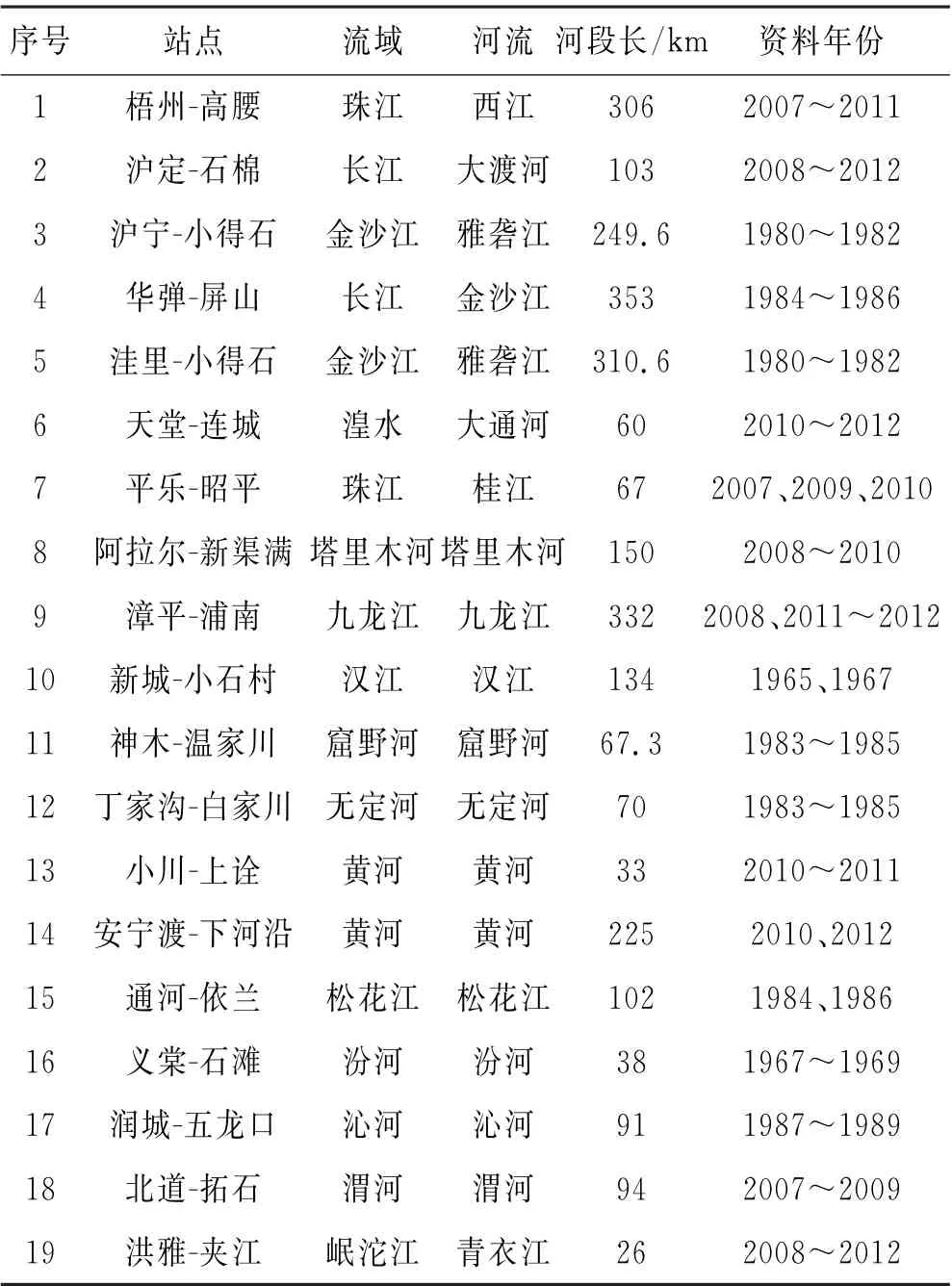
表1 演算河段资料概况

2.2 参数率定

率定期和检验期见表2.

将双变量模型与马斯京根模型同时进行参数率定，并进行检验.参数率定使用最小二乘法，参数率定结果见表3.

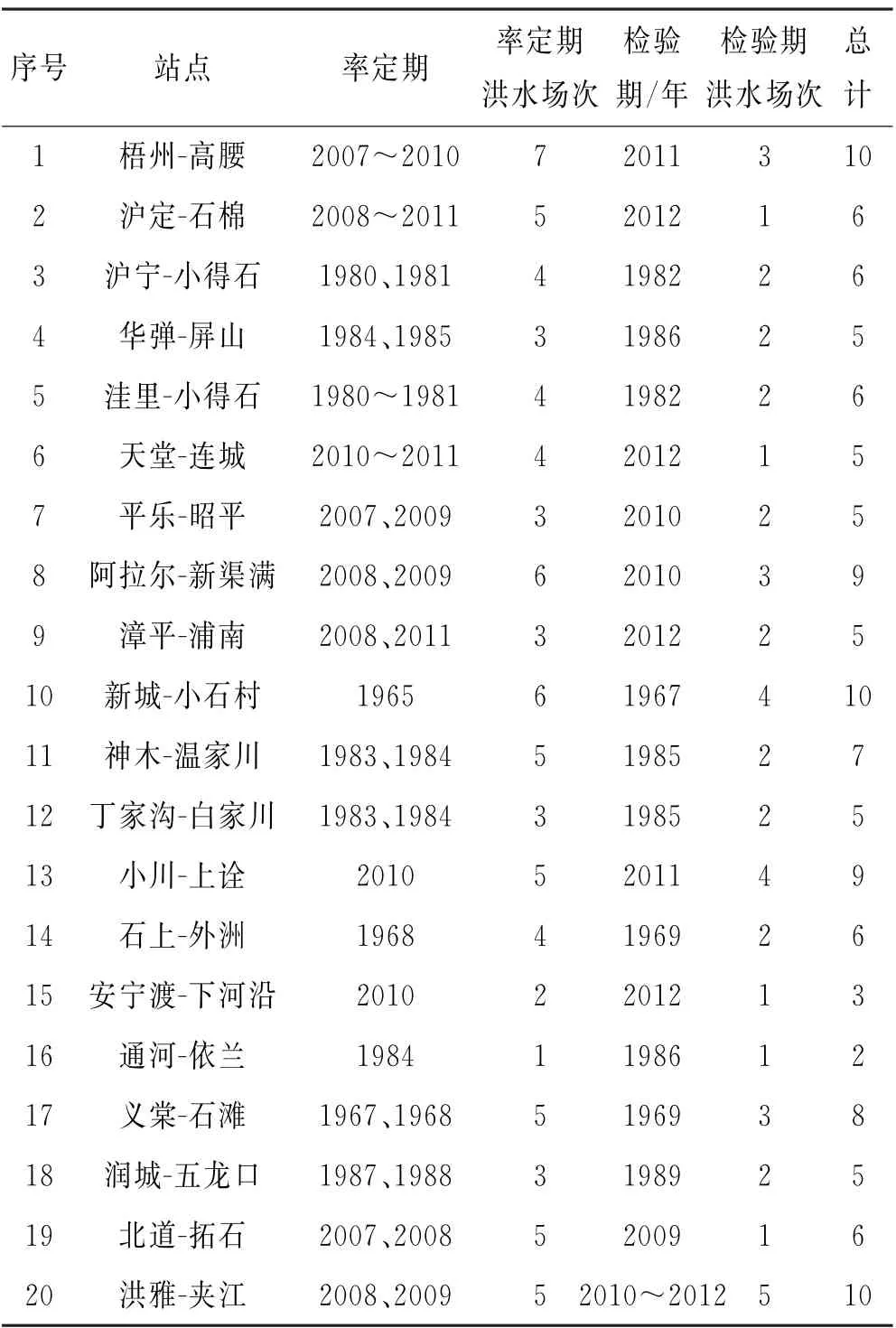
表2 率定期及检验期资料情况

表3 参数率定结果

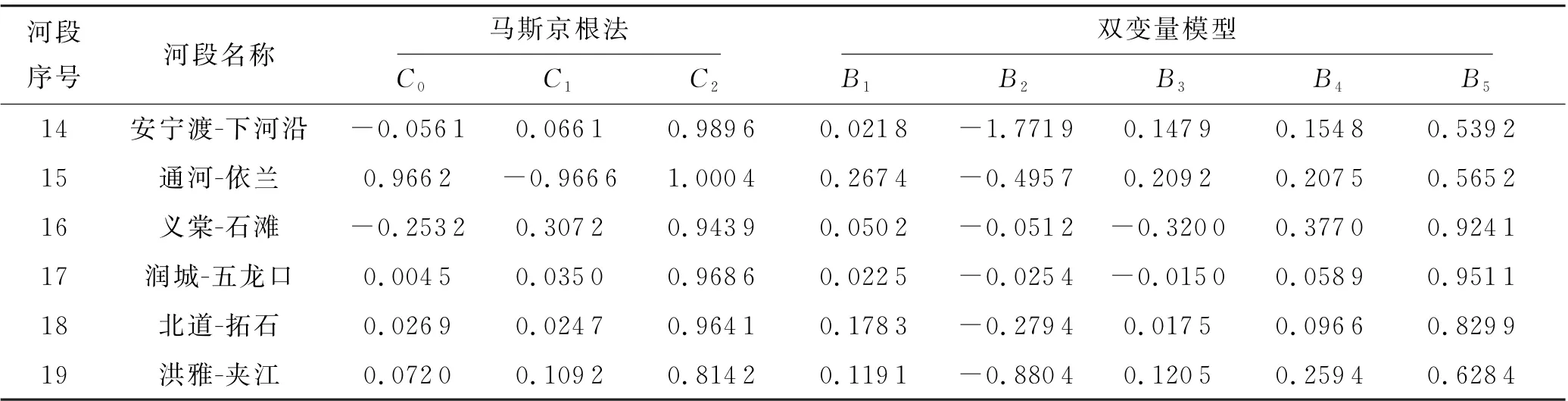
续表3 参数率定结果

2.3 结果分析

计算结果见表4.表中DC(Ma)表示马斯京根法率定期的确定性系数；VDC(Ma)表示马斯京根法检验期确定性系数；DC(SBL)表示双变量模型率定期确定性系数；VDC(SBL)表示双变量模型检验期的确定性系数；效果一栏“++”表示率定期和检验期确定性系数都提高，“+”则表示率定期和检验期部分场次确定性系数提高.

表4 河段率定期及检验期效果统计表

由此可见，由双变量模型所得的平均确定性系数较马斯京根法更高.在率定期由0.596提高到0.764，检验期由0.461提高至0.642，与实际的流量过程更接近.具体来看，大部分河段的确定性系数均高于马斯京根法.在19场洪水中，有15场在率定期和检验期双变量模型的效果均好于马斯京根，另外4场也有不同程度的提高；对于马斯京根法模拟较差的洪水，双变量模型可以得到较好的效果，如第9场，在率定期确定性系数由-0.451 提高到0.542，检验期由0.168提高到0.610，均有很明显的提升；对于马斯京根法模拟较好的洪水场次，如第7场、第16场检验期的洪水，确定性系数分别从0.723 降到0.719，从0.670降到0.660，模拟效果区别不明显.因此，双变量模型模拟更稳定.

选取洪水场次最多的洪雅-夹江河段为例，以前2年的5场洪水作为参数率定，后3年的5场洪水作为检验.检验结果见表5.

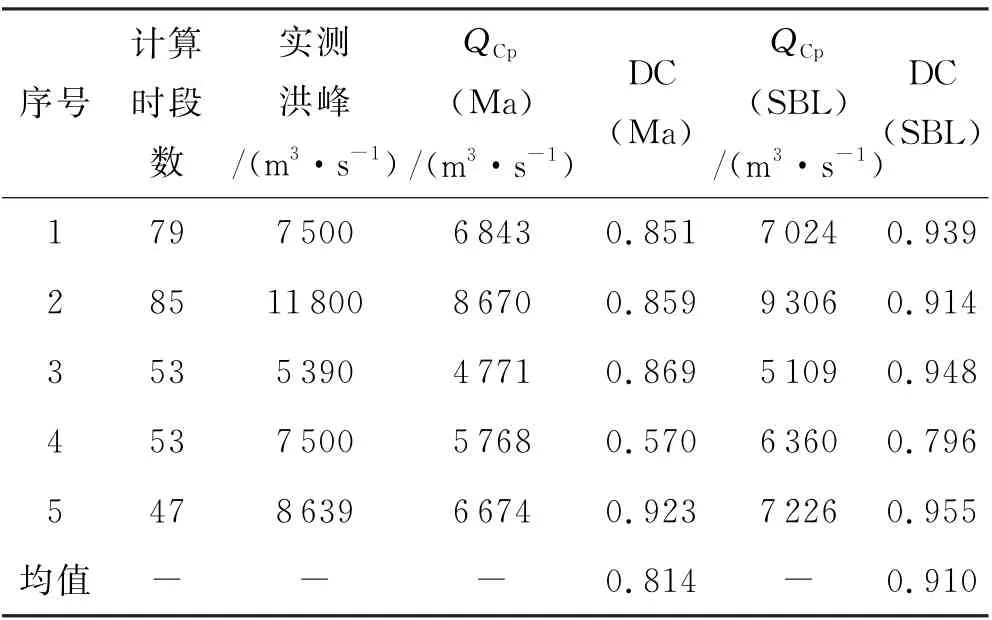
表5 洪雅-夹江河段检验期结果统计表

QCp(Ma)和QCp(SBL)分别表示马斯京根法和双变量模型的模拟流量，DC(Ma)和DC(SBL)分别是马斯京根法和双变量模型的确定性系数.对于每一场洪水，均是新的模型峰值更好，确定性系数更高，与上述19个河段的演算结果一致.图1是1 号洪水的模拟效果图，图2是3号洪水的模拟效果图.从过程模拟来看，显然，新的模型与实测流量过程更为接近，过程拟合更好，洪峰位置较为明显，峰现时间也更接近.