异结构超混沌系统的自适应函数投影同步

张晓青

(太原工业学院理学系,山西太原 030008)

1990年，大洋彼岸的马里兰大学Ott[1]等人实现了对混沌吸引子不稳定周期轨道的控制，同年美国学者Pecora 和Carroll[2]二人在电路实验中观察到耦合混沌系统的同步现象。这些史无前例的开创性工作激起了人们对混沌机理的研究。随着研究的深入，提出了多种混沌同步的概念，比如，投影同步[3]，错位投影同步[4]，函数投影同步(FPS)[5-7]等。文献[5]通过设计滑模面，实现了多个整数阶混沌系统的组合函数投影同步。文献[6]设计积分滑模面，实现了分数阶统一混沌系统的FPS。文献[7]研究了两个纳电子整数阶超混沌系统的FPS，并且利用Lyapunov 理论设计了控制输入项。文中讨论异结构超混沌系统之间的FPS。利用Laplace 变换，将分数阶微分转换到Laplace 域中，然后用整数阶微分去逼近分数阶微分，把问题转化成不同维数整数阶混沌系统之间的同步。通过减少驱动系统的维数，达到驱动和响应系统的维数一致，基于Lyapunov 稳定性理论设计了非线性控制输入和参数辨识规则。最后利用MATLB验证所设计方案的合理性。

1 函数投影同步方法描述

驱动和响应系统定义如下：

其中：

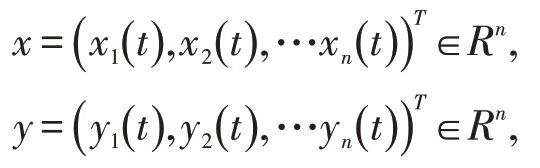
分别是系统(1)和系统(2)的状态向量。F,G：Rn→Rn为连续向量函数，u()x,y为非线性控制输入机制。

定义1针对系统(1)和系统(2)，如果存在一个尺度函数对角矩阵K(t)=diag(k1(t),k2(t),…,kn(t)),ki(t)≠0 使得成立，则说系统(1)，(2)处于函数投影同步(FPS)状态[8]。

2 分数阶Wang 系统和整数阶超混沌Lü 系统的函数投影同步

2.1 系统描述

分数阶超混沌Wang 系统[9]的动力学模型如下：

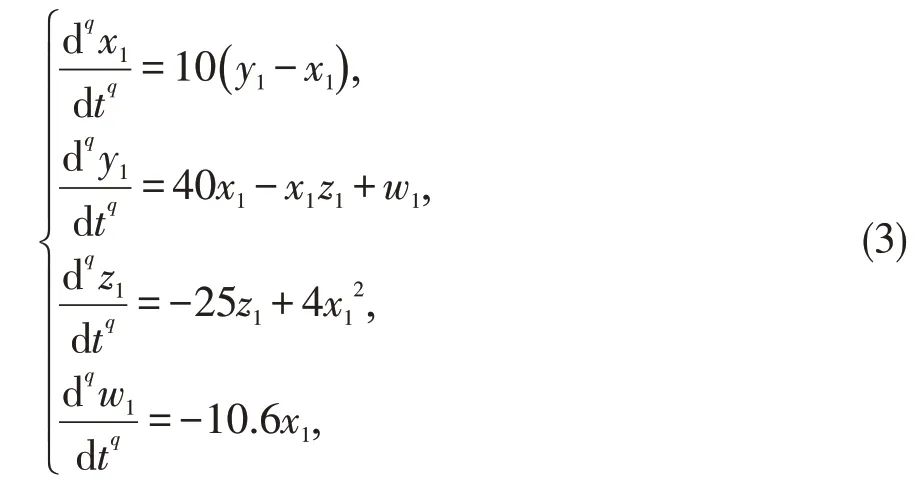
当q=0.95，系统初值分别取值为x1(0)=15y1(0)=20，z1(0)=10，w1(0)=40 时,Wang 系统处于超混沌状态。

整数阶超混沌Lü 系统的形式如下：

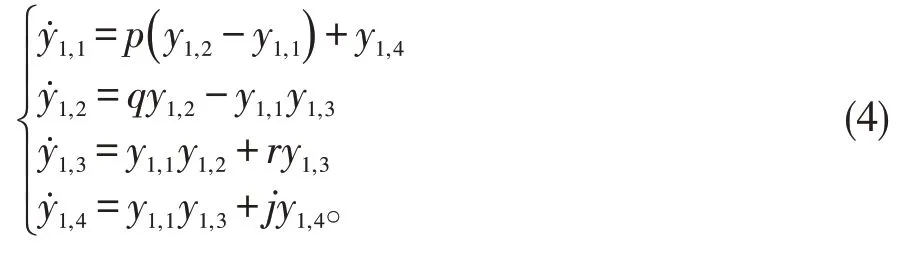
当未知参数p，q，r，j取值为(p,q,r,j)=(36,20,-3,1)，系统初值取为y1,1(0)=1，y1,2(0)=2，y1,3(0)=3，y1,4(0)=4 时，整数阶超混沌Lü 系统处于超混沌状态。

2.2 超混沌Wang系统和Lü 系统的函数投影同步

Wang 混沌系统(3)作为驱动系统，Lü 混沌系统(4)作为响应系统。在这一部分，将用整数阶微分来近似Wang 混沌系统，进而将分数阶超混沌Wang 系统和整数阶超混沌Lü 系统的FPS 问题变为阶数不同(十二阶与四阶)的整数阶超混沌系统之间的FPS。

对分数阶Wang 混沌系统(3)进行Laplace 变换,并假设其初始值均为零，则：

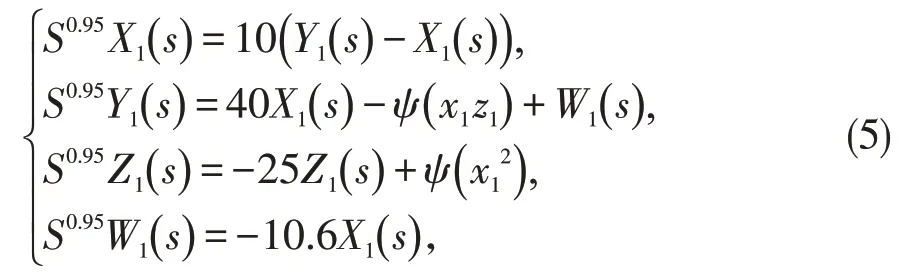
其中,ψ表示Laplace 算子，s为复变数。X1(s)=ψ[x1(t)]，Y1(s)=ψ[y1(t)]，Z1(s)=ψ[z1(t)]，W1(s)=ψ[w1(t)]。根据近似误差为1dB的1的展开式,有：

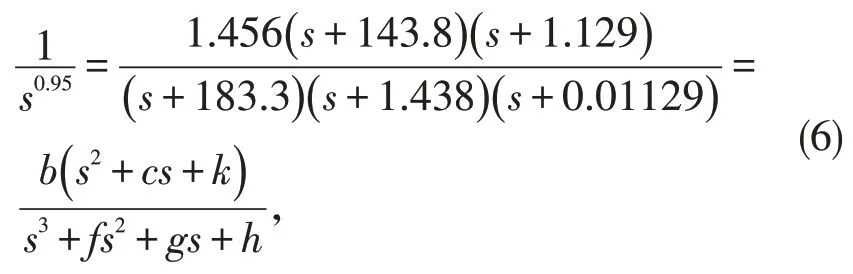
在(6)式 中b=1.456，c=144.929，f=184.749,g=265.6714，h=2.976，k=162.3502。

将式(6)代入式(5)得：

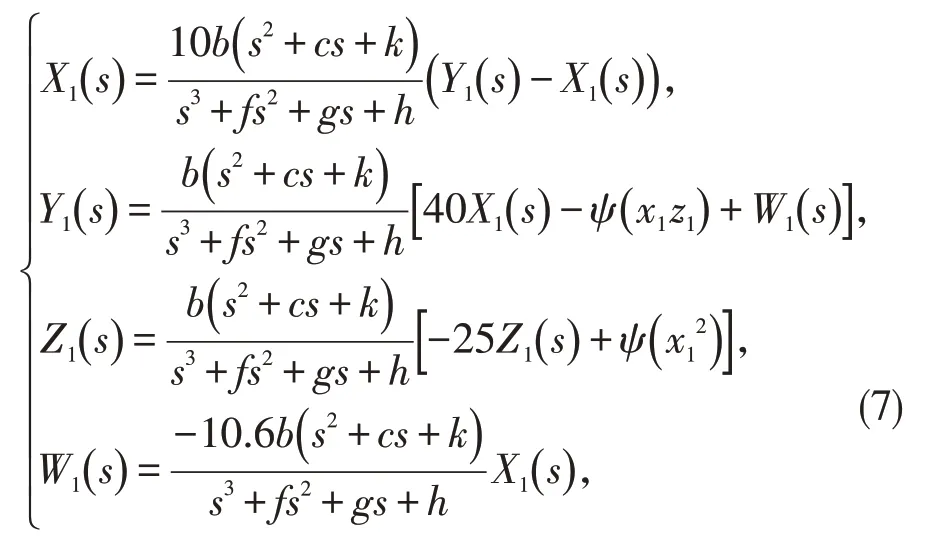
在时域中,令

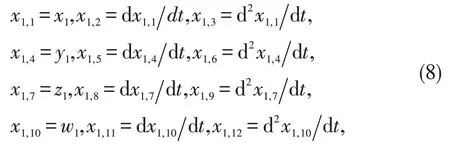
将(7)式进行Laplace 逆变换，可得分数阶Wang混沌系统的整数阶拟合方程如下：

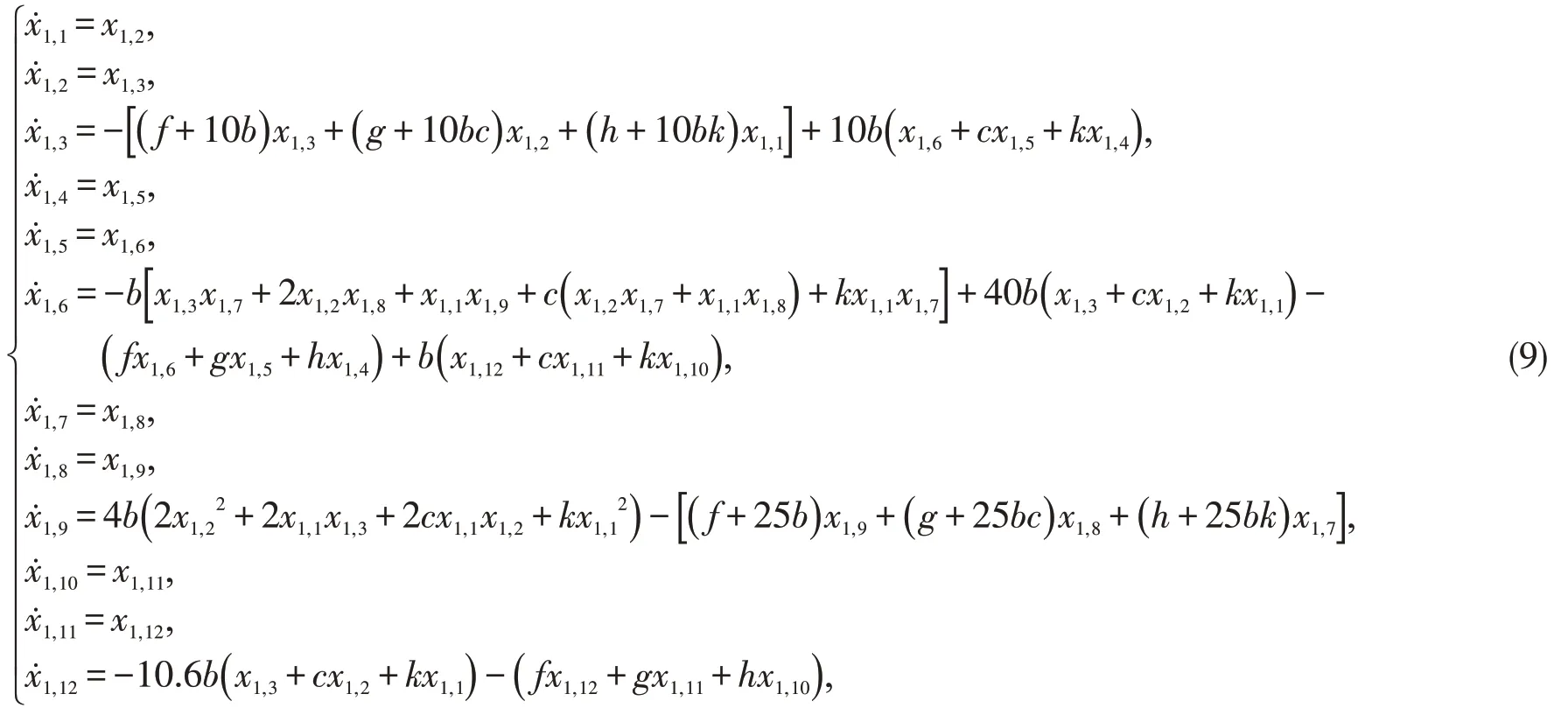
此处利用缩减驱动系统维数以达到驱动响应系统维数一致。降维后的驱动系统为：

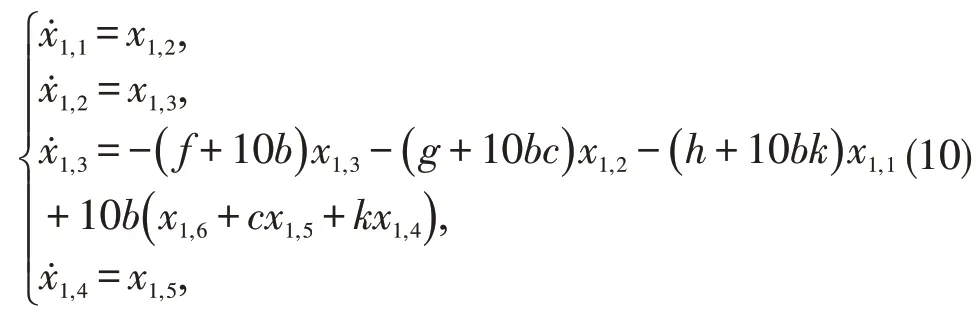
加入控制输入的响应系统如下：

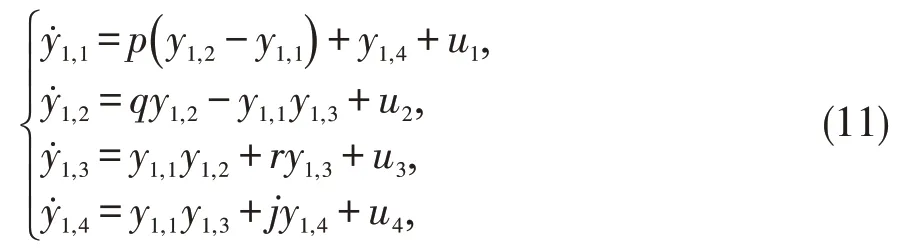
此处ui(i=1,2,3,4)为同步控制输入。

函数同步误差系统为：

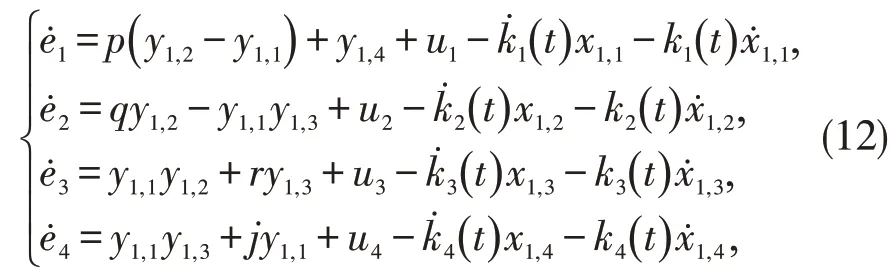
控制输入设计为：

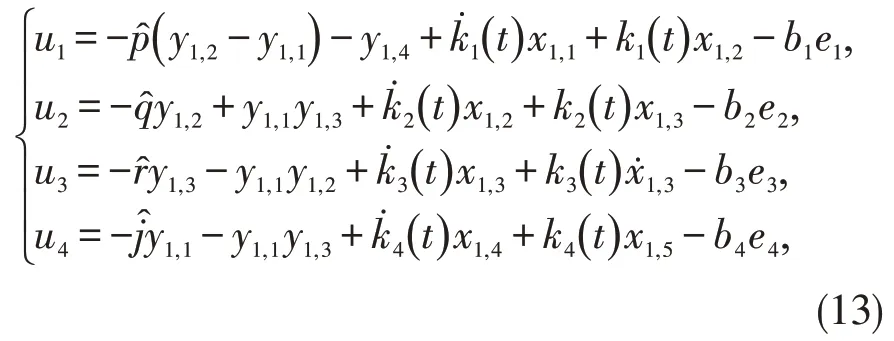
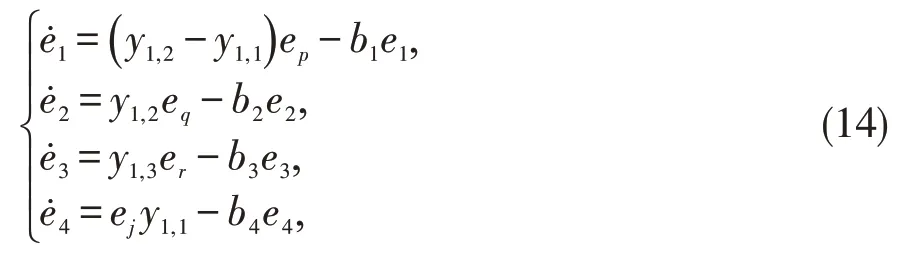
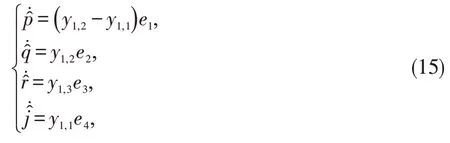
构造Lyapunov 函数如下：

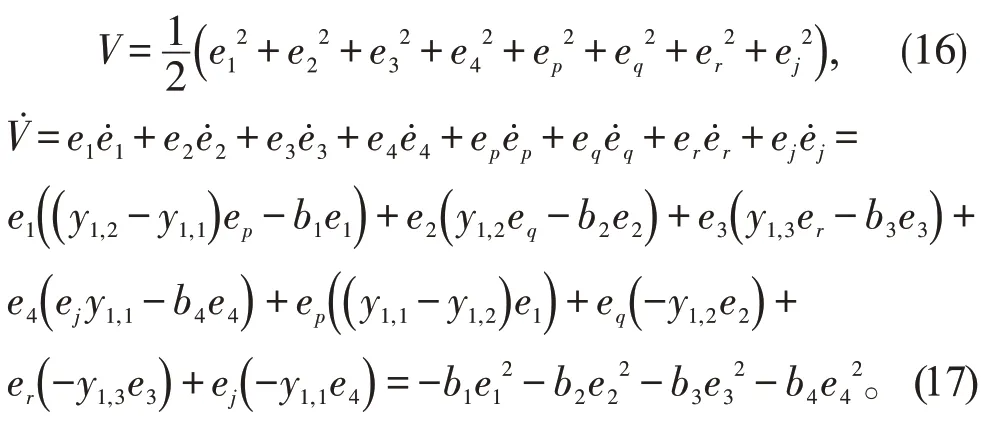
显然V≥0,成立，根据Lyapunov 理论，则当t逐渐增大的过程中，Wang 系统和Lü 混沌系统达到了FPS 状态。

2.3 数值仿真

用Matlab 软件进行数值仿真，系统(10)与(11)的初始值分别取x1,1(0)=0，x1,2(0)=0,x1,3(0)=15，x1,4(0)=0,y1,1(0)=1,y1,2(0)=2,y1,3(0)=3,y1,4(0)=4 。参数取为p=36，q=20，r=-3，j=1，标度函数ki(t)(i=1,2,3,4)分别取为k1(t)=sint，k2(t)=sint+1，k3(t)=cost-1,k4(t)=cost+1，bi分别取b1=7，b2=8，b3=20，b4=6 时，Wang系统和Lü 混沌系统的FPS误差变化如图1所示。很显然两系统在短时间内达到了FPS 状态。图2 为Lü 系统的未知参数p,q,r,j随着时间变化的过程，未知参数的估计值很快回归到理想值。

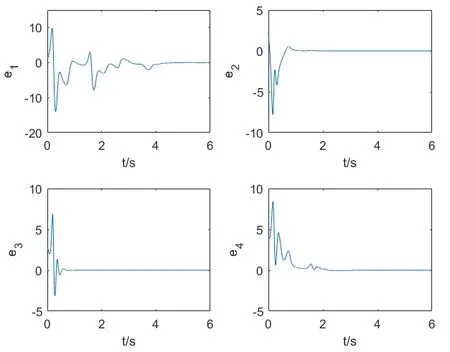
图1 误差曲线

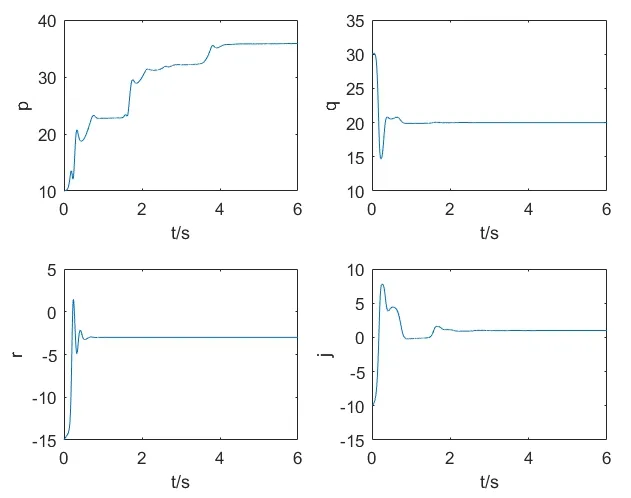
图2 Lü 系统的参数估计曲线

3 结论

把Laplace 变换作为工具，得到分数阶Wang 混沌系统的近似整数阶混沌系统。针对整数阶混沌系统之间的同步，设计了控制输入机制和对应的参数变化规律使驱动系统和响应系统实现了FPS 状态。仿真结果和理论推导相呼应，说明了所设计的控制输入的合理性。操作的方法为整数阶与分数阶混沌系统实现同步提供了新的思路。