基于热传导的高温作业专用服装设计研究

朱世昕 ,林志春 ,李 笑 ,郭 浩

(1.山西大同大学教育科学与技术学院，山西大同 037009；2.山西大同大学数学与统计学院，山西大同 037009）

1 问题重述

在高温环境下作业时，工作人员需穿着专用服装以避免灼伤。这种专用服装它由三层织物材料构成，分别是与外界环境接触的I 层，衣服内部从外到里的II、III 层，以及III 层与皮肤之间的IV 层空隙。设计专用服装时，为了降低研发成本、缩短研发周期，将体内温度控制在37 ℃的假人放置在实验室的高温环境中实验，测量并记录假人皮肤外侧的温度，并建立数学模型。

问题：

（1）专用服装材料的某些参数值已给出，对环境温度为75 ℃、II 层厚度为6 mm、IV 层厚度为5 mm、工作时间为90 分钟的情形开展实验，测量得到假人皮肤外侧的温度。建立数学模型，计算温度分布，并生成温度分布的Excel文件；

（2）当环境温度为65 ℃、IV层的厚度为5.5 mm时，确定II 层的最优厚度，确保工作60分钟时，假人皮肤外侧温度不超过47 ℃，且超过44 ℃的时间不超过5分钟；

（3）当环境温度为80 ℃时，确定II 层和IV 层的最优厚度，确保工作30 分钟时，假人皮肤外侧温度不超过47 ℃，且超过44 ℃的时间不超过5分钟。

2 模型建立与求解

2.1 问题1的分析与求解

2.1.1 对假人皮肤外侧温度的测量数据分析

在假人外侧皮肤温度测量实验中，假人皮肤温度随时间推移逐渐升高。在所给实验数据中，记录下假人皮肤外侧以秒为单位，在5 400 秒的温度变化情况，并用MATLAB 拟合出温度时间曲线，如图1所示。

图1 温度时间图

可以看到，28分钟后的温度几乎是稳定的，所以需要对数据采取抽样处理的方法进行处理。

2.1.2 对数据抽样分析

经研究，将数据每隔60 秒抽取一个温度测量值，并将每个时刻的对应温度值统计出来，整理成Excel表格，见表1。

表1 温度分布表

利用SPSS 对抽样数据建立温度曲线模型，所得温度变化曲线，如图2所示。

图2 温度变化曲线

建模过程中其模型统计及参数评估，见表2。

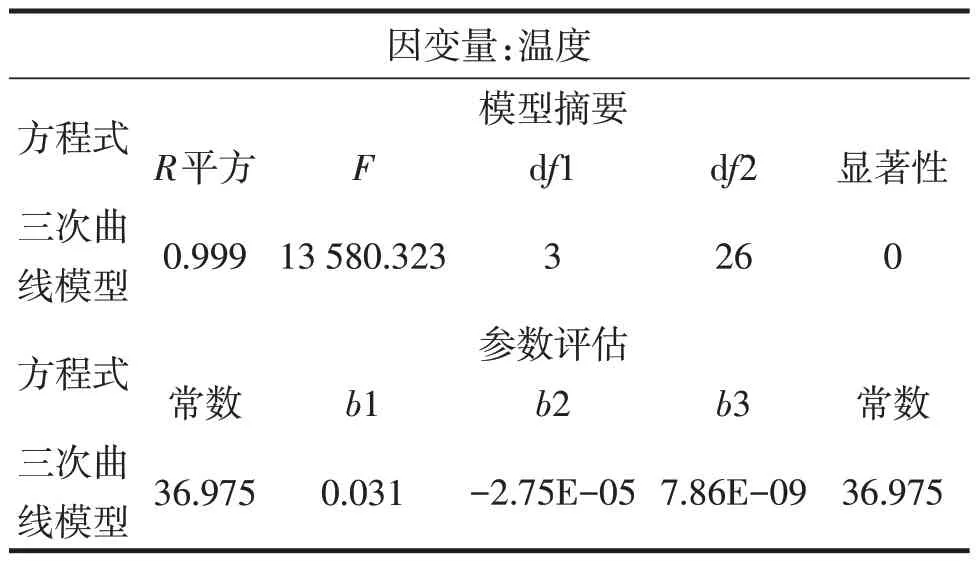
表2 模型统计及参数评估

2.1.3 利用SPSS拟合得数学模型

所建立模型为：

2.1.4 模型检验

在Excel表中代入模型，得到对应时刻的温度，以及模型所求温度与实际试验温度的差值，见表3。

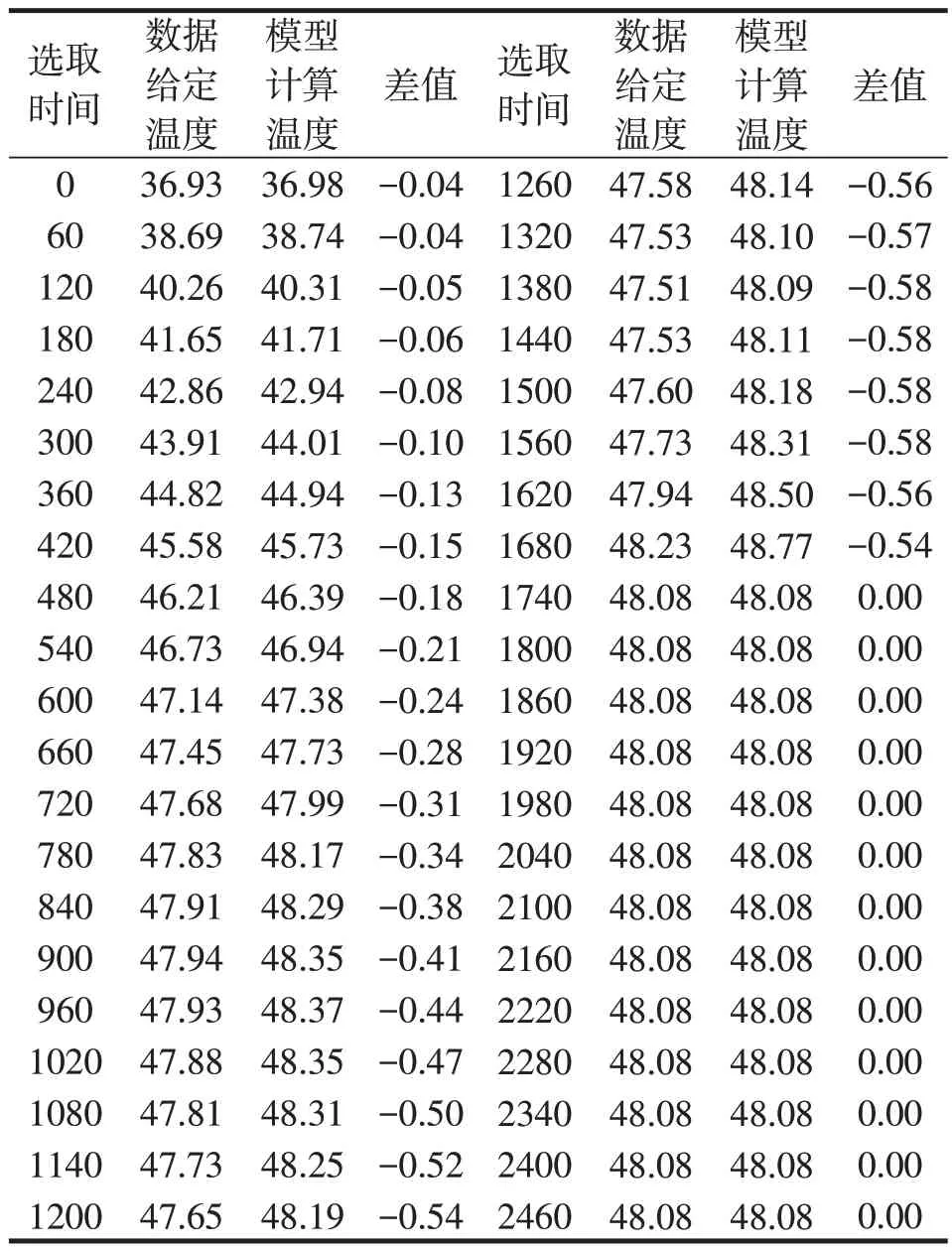
表3 假人皮肤外侧的测量温度和模型所求温度

2.2 问题2的分析与求解

热量传递是个复杂过程，可分解为三种不同的方式：导热、对流和热辐射。在问题中主要考虑导热和对流这两种传热方式，来探讨在高温作业服的热量传递过程。

热力学第二定律中指出，在温度差存在的情况下，热量总是会自发地从高温物体向低温物体传递，如图3所示。

图3 服装任意一层的截面示意图

其中δ为厚度，A为表面积，tw1和tw2分别为两个表面温度，且假设tw1＞tw2。那么在单位时间内从表面1到表面2的热流量Φ和材料两侧的温差Δt=tw1-tw2与热流方向和材料表面积A是成正比的，与平板的厚度δ是成反比的，即[1]：

在单位时间内通过单位面积的热流量为

2.2.1 求最优解模型

由能量守恒定律，物体内的任一微元体的热平衡式[1]：

热阻串联，如图4所示。

图4 热阻串联图

在图4 所示的热阻串联环境中,由热平衡式得出下列不等式（忽略内热源产热）

利用数学软件Matlab 得出第二层厚度的边界解为-11.162 795 34mm(排除)与1.067 574 32 mm，即解出第二层厚度最优解为1.067 574 32 mm。

2.2.2 检验模型

根据第一思路分析，最大的阻碍就是关于总传热系数的h求解，因此检验模型的第一步是求解h，对h的求解是建立在问题一的条件下的，并且假设总传热系数是1 个定值，不受其他因素干扰。下面我们分两步进行建模，在第三步中对最优解模型结论进行检验。

第一步：

将热流量密度作为中间桥梁列出热阻（关于所求厚度的函数）与总传热系数h之间的关系式[2-3]：

(1)对于式（6）第一式的右侧，文献[2]中围岩导热过程分析中，将高斯误差函数和人体与空气对流相关知识结合，进而得到式（6）的第一式右侧；

(2)为在一定程度上减小误差，方程中的t5取自附件一中工作时间内的加权平均温度tˉ=46.77℃，时间τ取附件一中的加权平均值τˉ=3236s（注：根据问题一中得到温度随时间的变化曲线，知分界时间为1680s，将时间以及温度分为两段，得以两段的权比为14：45，得出时间温度的加权平均值），然后利用数学软件Matlab直接求得：

h≈0.0020984W/(m2∙C)。

第二步：

将问题情境牵引回问题2中，根据思路一中“前后夹击”的方法，第四层的温度当成所求量t4，再根据由外至内以及由内至外，两面“夹击”求得t4。建立的方程是将外三层看成一个整体下进行的，依旧是以热流量密度q为中间桥梁，利用傅里叶定律以及热流量密度的定义将问题条件得出关系式：

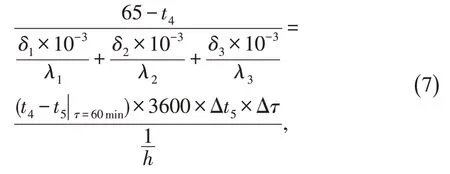
其中：t5|τ=60min=47℃，Δt5=47℃-44℃,Δτ=5 min。

第三步：

代值反解出t4，判断其是否违背客观现实。将第一步中求出的近似总传热系数与最优解模型得到的最优厚度σ2（涉及到的σ均以mm 为单位）代入式(7)中，反解出第四层的气体温度大约是48.60℃，由第四层跟人体之间的对流导热致使人体温度最高达到47℃的原理反推出第四层气体温度相差不大，并且这个结果与客观事实虽然有着一些差距，但误差是在可接受范围内的，也就是说，通过最优解模型得出的第二层的最优厚度是相对正确的。

2.3 问题3的分析与求解

问题3 与问题2 属同类问题，只是要确定的最优解变成了两个，为将问题3 的求解过程简化，直接利用问题2的求解过程。

将问题3转为线性规划问题[4-7]，最后利用数学软件直接得出所求两个最优厚度。

将式(5)进行扩充得到：

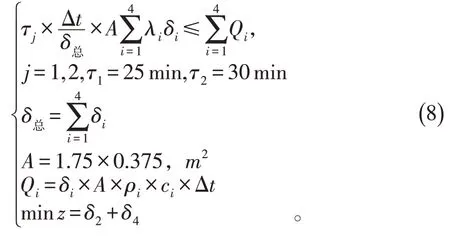
3 模型评价

3.1 模型优点

问题1的模型充分依据附件所给的假人体表温度数据，利用MATLAB和SPSS软件拟合出符合已给数据的曲线，该曲线R方为0.991，这说明拟合曲线跟实际数据拟合程度较高，体现了该模型的准确性。

问题2的模型以热能量守恒为基础，可较合理的求解出在特定温度下，经过一定时间后人体表面的温度，运用热能量守恒定律极大地在运算复杂度上降到了最低，避免了其他模型的繁复的计算。

问题3 与问题2 使用相同原理，因此可以得出第二层材料厚度与第四层材料厚度的函数关系式，通过线性规划求出两个最优解。

3.2 模型缺点

因为存在多种热传递方式，其中热辐射对实验影响过多，为简化问题，将这一因素舍去，导致建立的模型跟实际误差相对较大，再者对于材料表面积上的差异，将所有层面的表面积近似看成人体表面积，因此模型存在的误差会继续变大。