基于折射方向矢量的地球卫星星光折射导航新方法*
2020-06-02宁晓琳梁晓钰孙晓函房建成
宁晓琳,梁晓钰,孙晓函,房建成
(1.北京航空航天大学 前沿科学技术创新研究院·北京·100191;2.北京航空航天大学 仪器科学与光电工程学院·北京·100191)
0 引 言
随着载人航天、高分辨率对地观测及空间应用的发展,各类航天器对自主导航能力的要求更加迫切。自主天文导航由于具有导航精度较高、误差不随时间积累、抗干扰能力强以及可同时提供位置和姿态信息等特点,已成为一种有效的自主导航手段[1]。地平测量精度是影响地球卫星天文导航精度的最主要因素[2]。根据敏感地平方式的不同,地球卫星的自主天文导航可分为直接敏感地平和利用星光折射间接敏感地平两种方法[3]。直接敏感地平自主天文导航原理简单且易于实现,但是受地球敏感器精度的制约,导航精度较低,同时大气覆盖导致的地球边缘位置难以确定,也降低了导航的精度[4]。相比较于直接敏感地平的自主天文导航方法,星光折射间接敏感地平的自主天文导航方法只需要星敏感器就可以获得量测信息,且现阶段的星敏感器的测量精度要远高于地球敏感器,使得导航精度大幅度改善[1]。
星光折射自主导航的研究工作始于20世纪60年代,美国Draper实验室(Charles Stark Draper Laboratory,CSDL)在实施Apollo计划的过程中,就对利用天体掩星、星光在大气中的折射、星光穿越大气时的衰减等实现自主导航进行了研究[5-6]。1975年,CSDL研究了基于星光折射/色散的自主导航方案,提出了几种星光折射敏感器的设计方案,并于1979年开展了关于大气星光折射能否提供真实数据的研究,这是推动星光折射自主导航方法发展的重要一步。1980年,CSDL在研究了OAO-3卫星成功获取的大量星光折射数据后,推断星光折射导航将会是一种精度较高的导航方法。1984年,CSDL进一步对星光折射自主导航方案进行了误差分析和仿真研究,假定大气折射高度为25 km,以折射视高度作为观测量,一个轨道周期内观测40次折射星,利用卡尔曼滤波(Kalman Filter,KF)得到优于100 m的导航精度[4]。20世纪80年代初,法国国家空间研究中心以低轨观测卫星SPOT为研究对象,进行了基于星光折射的自主导航的研究,通过多次平流层气球试验对大气折射的特性进行了研究,预计此方法的导航精度可达300 m[7]。美国90年代的多任务姿态确定和自主导航系统(Multimission Attitude Determination and Autonomous Navigation,MADAN)将星光折射自主导航理论应用到实际,其定轨精度达到了100 m以下[8]。
近年来,有关星光折射导航的研究一直在进行,主要包括动态星表和选星方法[9]、不同航天器的应用[10]、组合导航[11]、星敏感器及其光学系统[12-13]、大气折射模型[14-15]、星光折射量测量[16]和滤波方法[17]等,这些研究从不同方面进一步促进了星光折射导航的发展。在以上的研究中,大多以折射视高度和星光折射角作为星光折射导航的量测量。尽管折射视高度的研究已经很成熟,但是折射视高度并不是直接观测量,它是由星光折射角和大气折射模型间接计算得到,引入的线性化误差较大。相较于星光折射视高度,以星光折射角作为量测量能够获得更高的导航精度,然而星光折射角也并不是最直接的观测量,而且以星光折射角作为量测量时,系统的量测模型成为隐函数,就需要隐式量测模型滤波方法[17]。同时,折射视高度和星光折射角都只能反映星光折射的大小一种折射信息,星光折射方向作为与卫星位置矢量直接相关的折射信息,对于提高卫星自主导航精度有很重要的影响[18]。相比较于折射视高度和星光折射角,星光折射方向矢量作为星敏感器最直接的观测量,既可以提供星光折射的大小,也可以提供星光折射的方向,是一种更为理想的星光折射导航量测量。
本文提出了一种基于折射方向矢量的星光折射导航新方法,并建立了相应的量测模型。与折射视高度和星光折射角相比,折射方向矢量将与卫星的位置矢量相关的星光折射方向这一信息引入导航算法。尽管星光折射方向矢量的获取方法相对简单,但是其量测模型计算十分复杂,导致导航系统量测模型无法用一个简单的量测方程表出。因此,本文选择UKF作为导航系统的滤波方法[19]。本文对相同仿真条件下,该方法的导航性能与折射视高度和星光折射角的导航性能进行了比较。仿真结果表明,所提出的基于折射方向矢量的星光折射导航方法的导航精度是最高的,相比折射视高度和星光折射角位置精度分别提高了23%和22%,速度精度提高了19%。
1 基于折射方向矢量的导航方法
本节详细地介绍了基于折射方向矢量的星光折射导航方法,包括折射方向矢量的获取方法,量测模型、状态模型和滤波方法。
1.1 折射方向矢量的获取
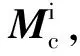

(1)
式中:f为星敏感器的焦距。
(2)

(a)折射星图
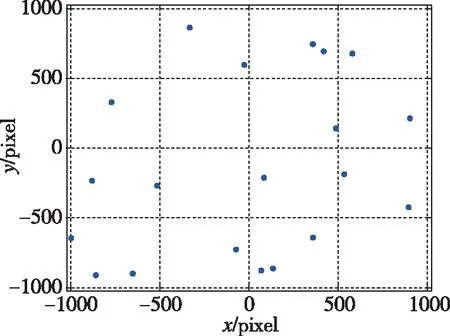
(b)模拟非折射星图
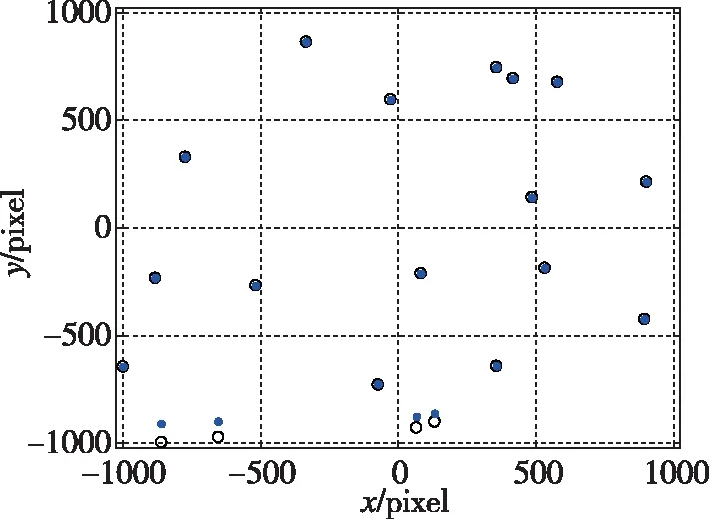
(c)折射星图和模拟非折射星图之间的对比
(3)
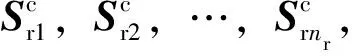
(4)
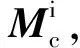
(5)
则有量测量
(6)
1.2 折射方向矢量的量测模型
折射方向矢量的量测模型无法用一个简单的方程式直接表达,是一个复杂的计算建立过程,主要包括星光折射角估计值的计算、惯性坐标系下的折射方向矢量估计值的计算两个重要步骤。
(1)根据星光大气折射模型和经验公式,折射视高度可以表示为[21]
ha=-21.74089877-6.441326lnR+
69.21177057R0.9805
(7)
(2)根据图2中的几何关系可得如下公式
(8)
式中:u=|r·S|;r是卫星的位置矢量;Re是地球半径;S为恒星在地心惯性系下星光方向矢量;Sr是星光折射方向矢量。


(9)

图2 星光折射导航原理

(10)
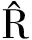
(11)
(12)
则惯性系下折射星的折射方向矢量可以表示为
(13)
则星光折射方向矢量的量测模型为
(14)
式中:v为折射方向矢量的量测噪声。
图3描述了建立折射方向矢量量测模型的流程图。
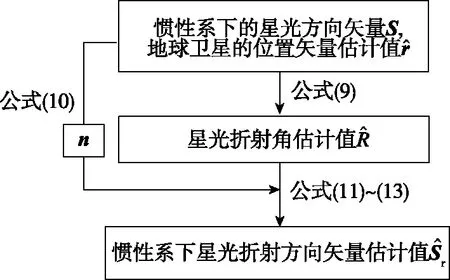
图3 量测模型建立流程图
1.3 状态模型
本文选择地心惯性坐标系下的轨道动力学运动方程作为系统的状态方程[22],如公式(15)所示。
(15)

1.4 滤波方法
通过折射方向矢量量测模型的建立过程可以看出量测模型是非线性的,不能简单地用一个方程表示。UKF等Sigma点滤波方法可以解决无法通过简单方程式表示测量模型的问题。因此,本文采用UKF方法估计卫星的位置和速度。

(16)

wi=1/[2(n+τ)]i=1,2,…,n
(17)

wi+n=1/[2(n+τ)]
(18)

本文所使用的标准UKF算法如下[19]:
(1)初始化
(19)
(2)计算采样点
(20)
(3)时间更新
χk|k-1=f(χk-1,k-1)
(21)
(22)
(23)
Zk|k-1=h(χk|k-1,k)
(24)
(25)
(4)量测更新
(26)
(27)
(28)
(29)
(30)
式中:Qk和Rk分别为系统和量测噪声协方差。当x(k)假定为高斯分布时,通常选取n+τ=3。
2 计算机仿真
本节对以折射方向矢量为量测量的星光折射导航系统性能进行仿真分析,并在相同仿真条件下,将其与以折射视高度、星光折射角为量测量的星光折射导航系统进行比较。同时,为了进一步验证该新方法的有效性,本节对星敏感器精度、轨道高度以及一个轨道周期内观测的折射星的数量等影响因素进行了分析。
2.1 仿真条件
2.1.1 轨道参数设置
本节以对地向三轴稳定卫星作为仿真对象,其轨迹由系统工具包(STK)[23]软件生成,卫星轨道运行图如图4所示。
(1)坐标系:J2000.0地心赤道惯性坐标系
(2)轨道参数设置为
长半轴a=6828.14 km,偏心率e=0,轨道倾角i=60°,升交点赤经0°,近升角距180°。
(3)轨道预报模型设置
利用 STK 提供的多种轨道预报器可以模拟星座系统星历预报,包括二体、J2Perturbation、J4Perturbation 预报器、高精度轨道预报器、长期轨道预报器。这里采用高精度轨道预报器作为卫星受摄运动模型,该模型内嵌了 JGM-3(70* 70)地球重力模型、固体潮、海潮模型,大气阻力模型,太阳光压模型,太阳、月亮引力场模型,能精确模拟卫星的轨道状态。
(4)姿态参数设置
卫星本体系的Z轴指向地心方向,X轴在轨道平面内与卫星速度方向一致,Y轴在轨道面的法线方向,与Z、X轴成右手系。
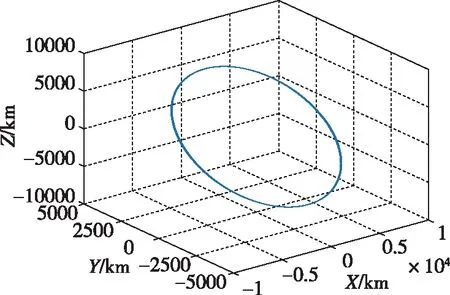
图4 卫星运行轨道图
2.1.2 星敏感器参数设置
星敏感器视场大小为10°×10°,所选星等为6.95m(14581颗),星敏感器精度3″,对应的像素误差为0.4266 pixels,星敏感器光轴与地心矢量之间的夹角为72°。
2.1.3 滤波参数设置
(1)滤波周期为3s;
(2)初始状态误差
ΔX0=[1000 m,1000 m,1000 m,1(m/s),
1(m/s),1(m/s)]T
(3)初始系统噪声协方差阵
P0=diag[103m2, 103m2, 103m2, 1(m/s)2,
1(m/s)2, 1(m/s)2]
(4)系统噪声方差阵
Q=2×10-2diag[1 m2, 1 m2, 1 m2, 10-3(m/s)2,
10-3(m/s)2, 10-3(m/s)2]
(5)量测噪声方差阵
若折射星像素坐标(u,v)的量测噪声方差阵R0为
R0=diag[0.42662, 0.42662, …,0.42662]
其中,由于每个量测量对应的是二维坐标,R0的维数是观测到的折射星数目的两倍。根据折射方向矢量、星光折射角、折射视高度、星点像素坐标相互之间的函数关系,可计算得三种量测量的量测噪声方差阵。
①折射方向矢量的量测噪声方差阵Rk
由于星敏坐标系下的折射方向矢量Sc与Sr有如下关系
(31)
又因为,
(32)
则第i颗折射星折射方向矢量与星点像素坐标具有一定函数关系,可表示为
Sri=fs(ui,vi)
(33)
则有折射方向矢量的量测噪声方差阵
(34)
其中,
(35)
② 星光折射角的量测噪声方差阵Rk′
第i颗折射星的折射角Ri可由如下公式计算得到
(36)
则第i颗折射星的折射角Ri和折射方向矢量的函数关系可以表示为
Ri=gR(Sri)
(37)
则星光折射角量测对应的量测噪声方差阵为
R′k=diag[H′iRkH′iT]
(38)
其中,
(39)
③ 折射视高度的量测噪声方差阵Rk″
由公式(7)可知
hai=hha(Ri)
(40)
则折射视高度对应的量测噪声方差阵为
(41)
其中,
(42)
2.2 仿真结果
2.2.1 三种导航方法的比较
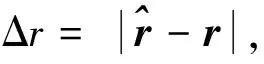

(a)位置估计合误差

(b)速度估计合误差

(a)导航收敛时位置估计合误差
(b)导航收敛时速度估计合误差
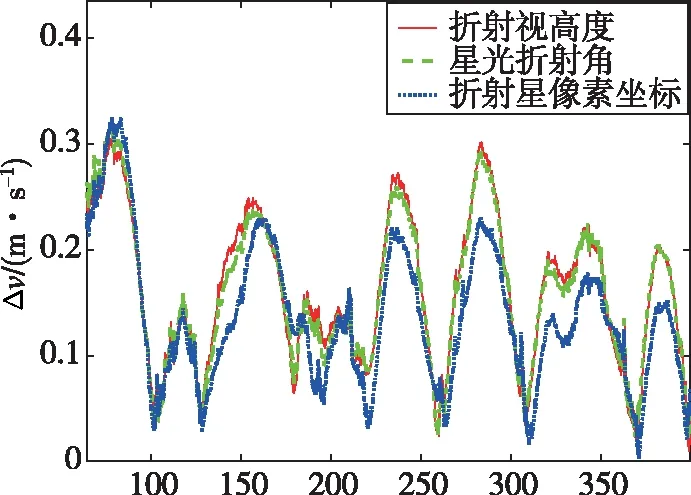
由图5可以看出三种量测量曲线的估计误差在100 min后逐渐收敛,且三条曲线都随着卫星轨道的周期进行着周期性地变化。三种量测量的位置估计误差曲线、速度估计误差曲线波动趋势基本一致。从图6和表1的数据可以看出,折射视高度作为量测量的导航性能最差,星光折射角次之,折射方向矢量的导航性能最好。相比较于折射视高度作为量测量,折射方向矢量作为量测量时的导航位置精度和速度精度分别提高了23%和19%;相比较于星光折射角作为量测量,折射方向矢量作为量测量时的导航位置精度和速度精度分别提高了22%和19%。这是因为折射方向矢量作为量测量能够同时反映星光折射的大小和方向两个重要导航信息,而折射视高度和星光折射角作为量测量只能反映星光折射大小一种信息,因此折射方向矢量具有更好的导航精度。
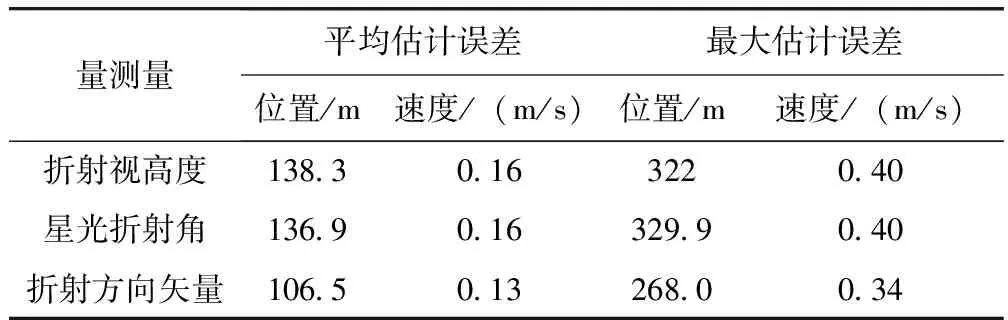
表1 折射方向矢量与折射视高度和星光折射角导航性能对比
2.2.2 影响因素分析
本节主要对导航系统精度的影响因素进行仿真分析,包括星敏感器精度、卫星轨道高度、一个轨道周期内观测的折射星数量。
(1)星敏感器精度
表2为不同星敏感器精度的基于折射方向矢量的星光折射导航系统的位置和速度误差(其他仿真条件和2.1节所述条件一致)。可以看出,导航结果的位置估计误差和速度估计误差都因星敏感器测量误差的变差而逐渐增大。因此,星敏感器精度是影响导航系统精度一个重要因素。
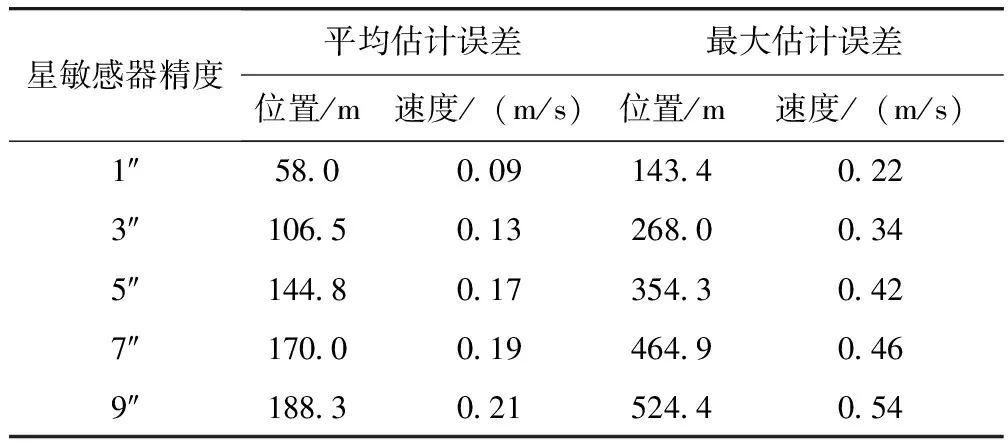
表2 不同星敏感器精度下的导航系统的位置和速度误差
(2)轨道高度
表3为不同轨道高度的基于折射方向矢量的星光折射导航系统的位置和速度误差(其他仿真条件和2.1节所述条件一致)。从表3中可以看出,随着轨道高度的增加,系统的位置估计精度和速度估计精度都逐渐变差。当轨道高度相对较高时,导航性能显著降低的原因是随着轨道高度的增加,能观测到的有效的折射星的个数减少变快,量测信息的减少导致了导航精度的下降。
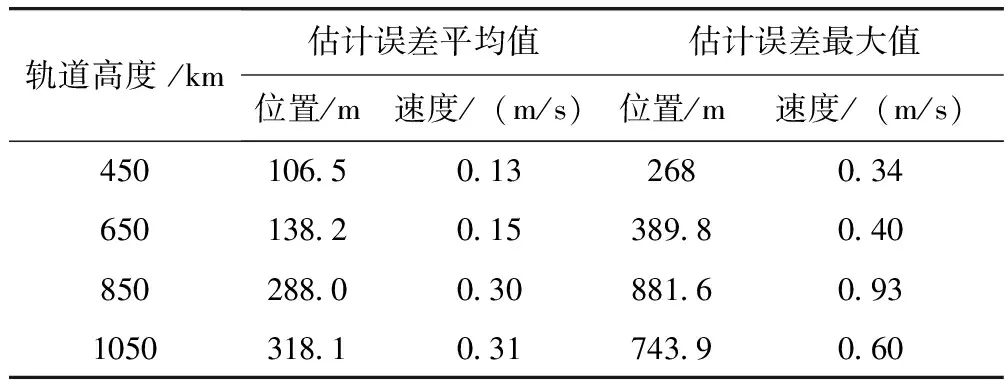
表3 不同轨道高度的导航系统的位置和速度误差
(3)一个轨道周期内观测的折射星数量
表4统计了星敏感器的探测星等分别为6.95 m、6.5 m、6 m和5.5 m时基于折射方向矢量的星光折射导航系统的位置和速度估计误差。表4 所示的结果表明,观测到的折射星的数量越多,导航精度就越高,反之,随着探测星等的降低,导航精度降低。
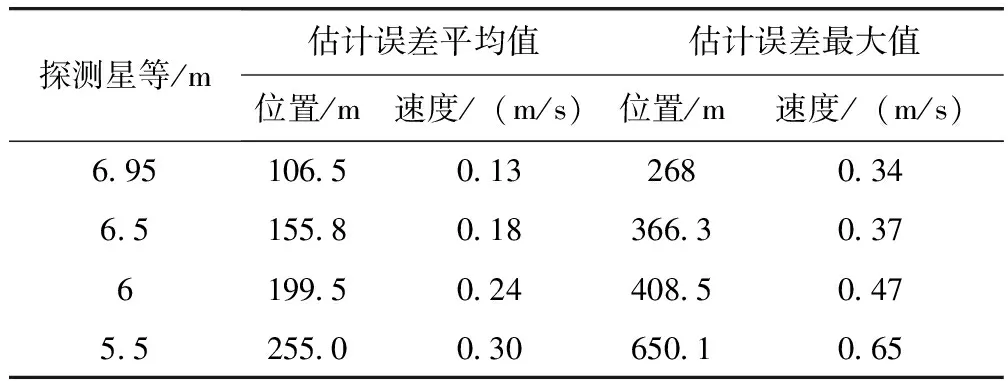
表4 不同折射星星等的导航系统的位置和速度误差
(4)大气折射模型误差
由于现有大气折射模型是基于1976年美国基本大气数据,工程应用中有待于实际大气观测数据的检验,也就是说现有大气折射模型存在不确定性,为了星光折射自主导航更好地应用于工程实践,非常有必要分析量测模型对导航精度的影响。在2.1节仿真条件下,令模型误差分别为0.1%、0.5%、1%、1.5%、2%,表5列出上述不同模型误差情况下的仿真结果。可以看出,随着模型误差的增大,导航系统的性能变差。
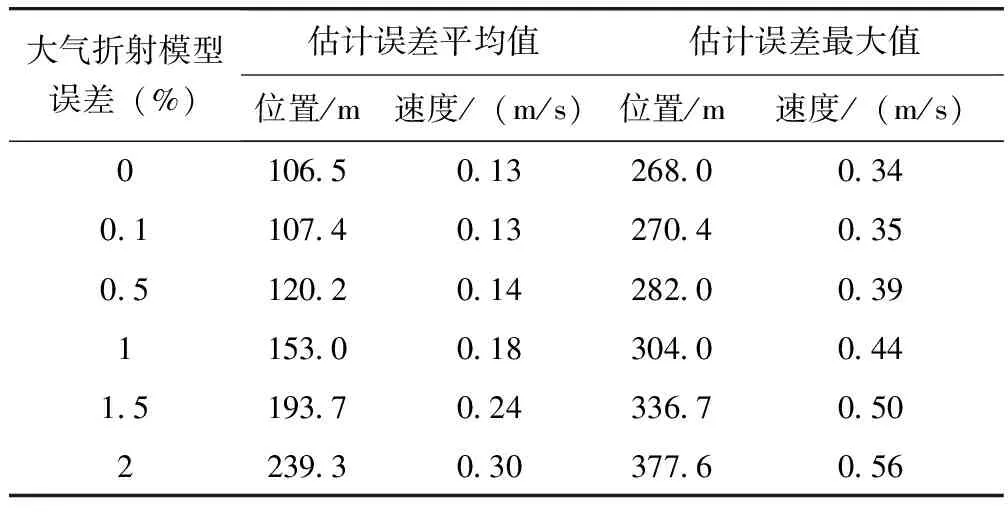
表5 不同大气折射模型误差的导航系统的位置和速度误差
3 结 论
本文提出了一种基于折射方向矢量的星光折射导航新方法,建立了折射方向矢量量测模型,对影响该导航方法精度的几个因素进行了分析。与仅使用星光折射角的折射信息的折射视高度和星光折射角相比,星光折射方向矢量可以增加星光折射方向的折射信息,通过仿真结果可以看出该导航方法提高了卫星位置和速度估计的准确性。所提出的方法可以为地球卫星星光折射自主导航的实际应用提供一定的指导。
