红外导引头平台底座拓扑优化设计*

洪文鹏，孟祥福，李 欢，陈 珂，江乐果

(1.陆军装备部驻南京地区军事代表局驻上海地区第三军事代表室·上海·201109;2.上海航天控制技术研究所·上海·201109;3.中国航天科技集团有限公司红外探测技术研发中心·上海·201109)

0 引 言

红外制导武器因制导精度高、抗干扰穿透烟雾能力强、隐蔽性和效费比高等优点，被广泛应用到侦察作战中[1]。红外导引头是红外制导武器的“眼睛”，它通常由光学探测组件、框架伺服机构、电路组合及结构件等组成，起到搜索、截获和跟踪目标的作用。平台底座作为框架伺服机构的重要零件，支撑着轴系零件和光学探测组件，其动静态特性和承载比直接影响红外导引头整体性能，因而必须对其进行结构优化设计[2-5]。

结构优化设计是在给定约束条件下，综合考虑结构的性能、材料及加工工艺等约束条件，按某种目标(如质量最小、成本最低、刚度最大等)求出最好的设计方案。按照设计变量的类型，结构优化设计可分为尺寸优化设计、形状优化设计和拓扑优化设计。虽然尺寸优化和形状优化起步比较早、技术较成熟，但产品在结构布局已定的情况下，设计人员对产品的更改程度就会受限，达不到理想的优化效果。而结构拓扑优化设计是在结构概念设计过程中，在给定设计目标和约束的情况下寻求最优的结构方案[6]，它的主要思想是在给定的设计区域内寻求最优材料的分布。所以在结构的设计和优化过程中，拓扑优化比其它优化方法更灵活、效率更高且实际应用价值更高[7-8]。

随着航空航天、国防工业、汽车、现代医学以及生物工程等领域的发展，人们对产品性能和轻量化的要求越来越高，使得拓扑优化技术得到了飞速的进步。例如焦洪宇等人对桥式起重机箱型主梁周期性拓扑优化设计[9]，刘成颖等人对面向机床整机动态性能的立柱结构优化设计研究[10]，张志飞等人对面向多目标的汽车悬架控制臂拓扑优化研究[11]。文中将拓扑优化技术应用到红外导引头平台底座结构设计中，以平台底座轻量化为设计目标，以不降低平台底座刚度和基频为约束条件，获得了平台底座最佳的拓扑形式。

1 拓扑优化理论

拓扑优化是一种根据给定的负载情况、约束条件和性能指标，在给定的区域内对材料分布进行优化的数学方法。其主要思想是在指定的可优化区域内找到材料的最佳分布，使结构的各项指标达到最合理的分配。目前比较成熟的优化方法有均匀化法、渐近结构法、变密度法等。其中，变密度法被广泛应用到拓扑优化设计中，成为工程设计最常用的方法之一，很多大型CAE软件都已开发出基于变密度法的拓扑优化模块[12]，文中将采用此方法进行拓扑优化设计。变密度法的提出是Mlejnek等人早期根据均匀化方法创造的。大致思路为：根据经验建立一个公式，用以确定每个单元的弹性模量与密度之间假定的函数关系，将材料的相对密度看成设计变量，实现结构的拓扑优化。为了方便去除多余的密度材料，将连续变量等价成无数个离散变量，使得其单元密度更好地趋近0～1的两端。在优化过程中，除了定义设计变量外，还要定义约束条件和目标函数。通常将结构柔度最小化定义为目标函数，将结构轻量化及节点应变量定义为约束条件，其变密度法拓扑优化数学模型[13]为

(1)

式中：ρ为相对密度，是设计变量；n为设计域中有限单元个数；C(ρ)为目标函数，表示结构的柔顺度；K为结构的总体刚度矩阵；U为结构的总体位移向量；F为结构所受的载荷向量；u为某一个节点的变型量；a为位移约束值；V为结构优化后的体积；vi为结构单元体积；ρ0为给定材料用量比率；v0为初始结构体积；V*为体积上限；ρmin为最小相对密度。

文中拓扑优化的流程为：(1)有限元模型的建立和网格划分；(2)受力分析、材料属性和边界条件；(3)优化结果；(4)结构与工程分析。

2 基于有限元的平台底座拓扑优化设计

2.1 有限元模型的建立和网格划分

平台底座底面与后部结构连接，上部立面的轴承安装孔安装偏航轴系，整个零件要有很高的结构刚度，同时需满足轻量化的要求。建立平台底座的原始模型如图1所示。

对原始模型进行网格划分，拓扑优化设计对网格的数量不敏感。为提高计算效率，对有限元模型网格数量进行控制，同时调整收敛情况，选取四面体网格进行网格划分，共划分5380个单元，11360个节点。

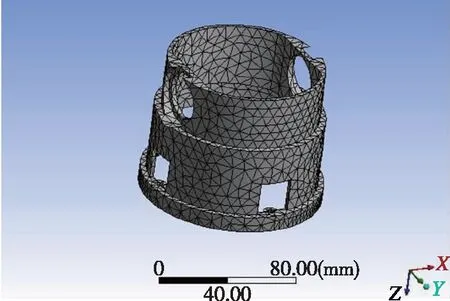
图1 平台底座初始有限元模型

2.2 受力分析、材料属性和边界条件

底座受力主要来源于光学探测组件和轴系零件等的过载载荷。底座承载的质量为984 g，对于沿导弹方向的力与导弹过载程度有关，按照15g的过载试验要求，可得最危险工况的受力为148 N，其余两个方向的受力为9.84 N。材料选择铝合金，底座底面与后部结构通过螺钉连接，其安装面的六个自由度全部约束。

2.3 优化结果

利用求解器进行求解，得到了底座拓扑优化后的密度分布图，如图2所示。其中红色为密度值接近零的区域，即材料去除的区域，灰色为材料需要保留的区域。根据分析结果可见，底座上面两个轴承孔位置附近的材料保留较多，而前后的材料保留较少，这说明轴承孔位置附近受载荷力较大，与力学原理相符。

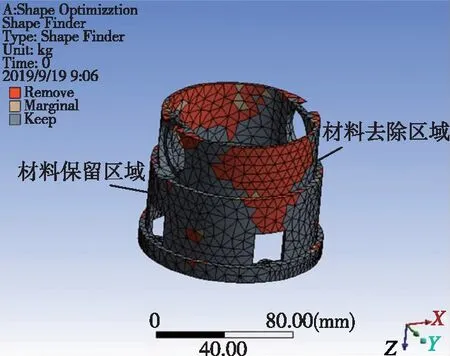
图2 底座拓扑优化后的密度分布图

3 结构与工程分析

根据拓扑优化的结果，对底座结构进行了重新建模。去除红色区域并使形状规则，在产品的尖锐边角处增加圆角结构。最终，底座拓扑优化后的三维模型如图3所示。

图3 底座拓扑优化后的三维模型

3.1 结构静力学分析

根据受力分析的结果，分别对底座上部轴承安装孔施加三个方向的静力。其中X、Y方向施加9.84 N，Z方向施加148 N，底座优化前后位移变形对比如图4所示。从结果中可以看出，X和Y方向的形变为亚微米级，优化前后变化小，对整机性能影响不大。Z方向的形变相对较大，其结果如表1所示。从表中可见，底座经拓扑优化后，质量由0.19 kg降至0.14 kg，减小了26.3%；最大变形量由2.6 μm降至2.4 μm，减小了7.6%；最大应力基本不变。可见，经拓扑优化后的底座实现了材料的最优分布，轻量化的同时结构静刚度有所提高，有利于红外导引头整机性能的提升。

(a)X方向优化前

(b)X方向优化后

(c)Y方向优化前

(d)Y方向优化后

(e)Z方向优化前

(f)Z方向优化后

表1 Z方向静力学分析结果对比

3.2 结构模态分析

模态分析是为了验证底座的动态特性，所以分别提取了结构优化前后的前三阶固有频率，结果如表2所示。各阶频率均有不同程度提升，其中基频由1432 Hz提高到1591 Hz，提高了11%，使整机系统的抗干扰能力和带宽上限得到提高。

表2 优化前后模态分析结果对比

4 试验验证

优化后的底座安装到产品中，然后将产品固定到专用工装上，通过专用工装与振动台刚性连接。将传感器分别粘在振动平台和离产品较近的工装上，进行随机振动和半正弦冲击试验。振动的功率谱密度最大值为0.05g2/Hz，频段为20～2500 Hz，振动试验曲线图如图5所示。试验过程中观测产品输出的图像和视频信号，产品工作正常，图像输出清晰，可以稳定跟踪目标。试验后复测产品性能，各项指标均与试验前一致。检查产品结构，无连接松动和结构损伤，说明平台底座动态刚度满足使用要求。

图5 振动试验曲线

5 结 论

通过对比优化前后平台底座的静态和模态结果，得到结论如下：①经拓扑优化后平台底座的静态特性变化为，质量由0.19 kg降至0.14 kg，减小了26.3%；最大变形量由2.6 μm降至2.4 μm，减小了7.6%；最大应力基本不变；②经拓扑优化后平台底座的动态特性变化为，基频由1432 Hz提高到1591 Hz，提高了11%。

研究结果表明，经拓扑优化后的平台底座，实现了轻量化的目标，结构更趋合理，同时静刚度和基频也有所提高。该方法也可应用到其它产品零件的优化设计中，将大大提高工程效率。