基于2维鲸鱼优化加权的WGG-Otsu算法的钢板表面缺陷图像分割
2020-06-01张东洋杨永辉储茂祥
张东洋,杨永辉,储茂祥,邓 鑫
(辽宁科技大学 电子与信息工程学院,辽宁 鞍山 114051)
随着工业技术的发展,对钢材的质量有更高要求[1],钢的板表面缺陷是影响钢板质量的重要因素.在钢材生产过程中,不同原因使钢材表面出现划痕、裂纹、氧化铁皮等缺陷[2-4].基于机器视觉的表面缺陷检测已成为研究热点,而表面缺陷图像分割是表面缺陷检测过程中的一个重要环节[5].图像分割方法有:阈值分割、区域生长分割、边缘分割方法等,其中阈值分割方法因计算简单、运算效率高、易实现,得到广泛应用.常见的阈值分割算法有:最大熵图像分割[6]、最小误差[7]和Otsu算法[8]等.Otsu算法是一种自适应阈值分割算法,分割效果良好,但其只考虑图像灰度,未考虑像素与邻域像素间的联系,易受噪声影响.文献[9]提出2维灰度级-平均灰度级-Otsu(grayscale-average grayscale-Otsu,简称GAG-Otsu)算法,算法抗噪能力有所提高,但去噪效果不很理想,且计算量大.文献[10]提出2维灰度级-梯度-Otsu(grayscale-gradient-Otsu,简称GG-Otsu)算法,总体上来说算法在分割精度和效率上均有所提高,但对信噪比较小的钢板表面缺陷图像的分割精度仍不高.为进一步提高缺陷分割精度,笔者在2维GG-Otsu算法的基础上,加上权重因子得到2维加权的灰度级-梯度-Otsu(weighted grayscale-gradient-Otsu,简称WGG-Otsu)算法,提高分割精度.将Otsu算法与各种优化算法结合,能提高图像的分割效率. 相比粒子群优化算法[11]、狼群优化算法[12]、遗传算法[13],鲸鱼优化算法收敛速度更快、精度更高[14].因此,笔者拟将鲸鱼优化算法与2维WGG-Otsu算法相结合,构建2维鲸鱼优化加权的灰度级-梯度-Otsu(whale optimized weighted grayscale-gradient-Otsu,简称WOWGG-Otsu)算法,以提高图像分割精度及效率.
1 2维GG-Otsu算法
2维GG-Otsu算法原理如下:假设f(x,y)(1≤x≤M,1≤y≤N)为一幅大小为M×N的图像中像素点的像素值,g(x,y)为高斯平滑后的此图像中像素点的像素值.2幅图像的灰度级均为L.F(i,j)是f(x,y)与|f(x,y)-g(x,y)|构成的2元组,F(i,j)=(f(x,y),|f(x,y)-g(x,y)|).图1为F(i,j)直方图的区域划分.图1中,F(i,j)的2维直方图被(t,s)划分成4个区域.将|f(x,y)-g(x,y)|过大的2,3区域的点视为噪声点,0,1区域作为背景及目标点.因此,在计算最佳分割阈值时,只需计算0,1区域的像素点.
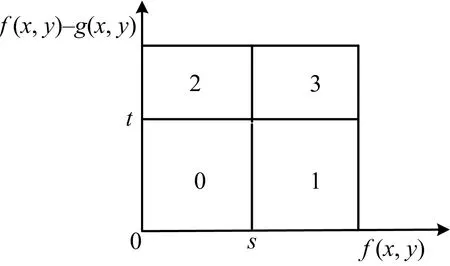
图1 F(i,j)直方图的区域划分
设二元组F(i,j)出现的次数为nij,则对应的联合概率密度Pij为
(1)
假设分割阈值为(t,s),则区域0,1对应的概率分别为
(2)
(3)
区域0,1的均值向量分别为
(4)
(5)
F(i,j)直方图的总均值向量为
(6)
2维GG-Otsu算法钢板表面缺陷图像的类间方差和为
(7)
2 2维WOWGG-Otsu算法
2.1 2维WGG-Otsu算法
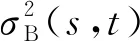
令
ω=1-Pt,Pt=Pt-k+Pt-k+1+…+Pt-1+Pt+Pt+1+…+Pt+k-1+Pt+k,
其中:Pt为阈值在区间(t-k,t+k)的分布概率[15].
基于2维WGG-Otsu算法的钢板表面缺陷图像的类间方差和为
ω{ω0(u0i-uzi)2+ω0(u0j-uzi)2+ω1(u1j-uzi)2+ω1(u1i-uzi)2}.
(8)
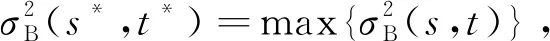
2.2 鲸鱼优化算法
在鲸鱼优化算法中,每头座头鲸的位置代表一个可行解.座头鲸在捕食过程中,以概率Pi进行收缩形式狩猎,以概率(1-Pi)进行螺旋形式狩猎.座头鲸在捕食前期,为寻找更好目标,在鲸群中随机找一头鲸为最优位置更新鲸群位置,以增强全局搜索能力.整个捕食的数学模型如下
(9)
其中
D1=|CX*(t)-X(t)|,Dp=|X*(t)-X(t)|,
(10)
其中:β为(-1,1)中的随机数;α为常数;t为当前迭代次数,Tmax为最大迭代次数;A,C为调整系数;r1,r2是(0,1)中的随机数;a的值随迭代次数t的增加从2线性下降至0.
2.3 2维WOWGG-Otsu算法
笔者将2维WGG-Otsu算法与鲸鱼优化算法结合,得到2维WOWGG-Otsu算法. 2维WOWGG-Otsu算法没有使用穷举法寻找最佳阈值,而是采用座头鲸捕食的方式,尽快找到一组解(s*,t*),使式(8)的值最大.2维WOWGG-Otsu算法步骤为:
步骤1 设鲸的数量为N,最大迭代次数为Tmax,概率Pi为0.5,座头鲸活动范围为[0,255].如果座头鲸位置超出活动范围的最小值Lb,则将座头鲸位置定义为0;如果座头鲸位置超出活动范围的最大值Ub,则将座头鲸位置定义为255.
步骤2 计算个体的适应度,将适应度最大的个体位置作为最优位置Pbest.
步骤3 当P>0.5时,以螺旋形式更新鲸群的位置;当P≤0.5,A≥1时,进行随机搜索,更新鲸群位置,以防陷入局部最优;当P≤0.5,A<1时,以收缩形式更新鲸群位置.
步骤4 若达到最大迭代次数,则输出最佳阈值(s*,t*),否则重复步骤2,3,直至达到最大迭代次数.
3 实验结果及分析
仿真实验用Matlab R2016b编写程序.设置鲸的数量N=15,最大迭代次数tmax=10.式(8)中常量α取1.鲸鱼位置的上界Ub=255,下界Lb=0.变量a随迭代次数的增加,线性递减.
实验使用的钢板表面缺陷图像来自东北大学发布的钢板表面缺陷数据集[16].在该数据集中选择4类钢板表面缺陷图片用于实验.图2为4种算法对带有夹杂、斑块、压入氧化铁皮和划痕4类缺陷图像的分割结果.由图2可知,夹杂、斑块和压入氧化铁皮的颜色相对于背景颜色较暗、灰度值低,分割后钢板表面缺陷呈黑色;划痕颜色相对于背景颜色较亮、灰度值高,分割后划痕呈白色. 对照原图易知,2维WGG-Otsu算法及2维WOWGG-Otsu算法的分割效果比2维GG-Otsu算法及2维最大熵算法的好.

图2 4种算法对图像的分割结果
为了定量比较4种分割算法对4类钢板表面缺陷图像的分割效果,使用Dice相似性系数(DSC)作为评价指标[17],其定义式为
DSC(A,B)=2(A∩B)/(A+B),
(11)
其中:A为标准图像,B为待评价图像.DSC值越大,则图像的分割效果越好,反之越差.
4种算法对钢板表面夹杂缺陷图像的分割性能比较如表1所示.
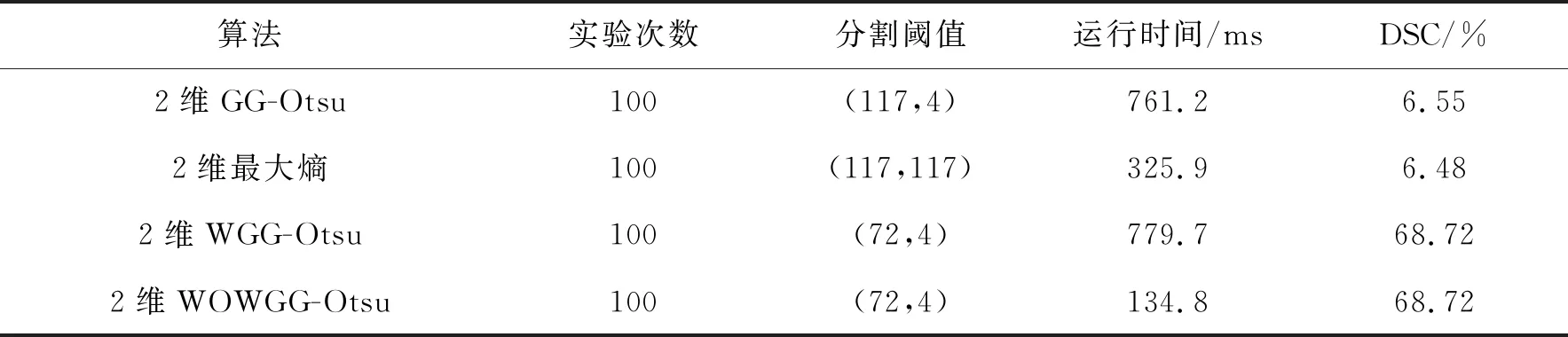
表1 4种算法对夹杂缺陷图像的分割性能比较
从表1的分割阈值可知,相对于2维GG-Otsu算法及2维最大熵算法,2维WGG-Otsu算法及2维WOWGG-Otsu算法的分割精度高.从运行时间可知,2维WOWGG-Otsu算法的分割效率最高.
4种算法对钢板表面斑块缺陷图像的分割性能比较如表2所示.
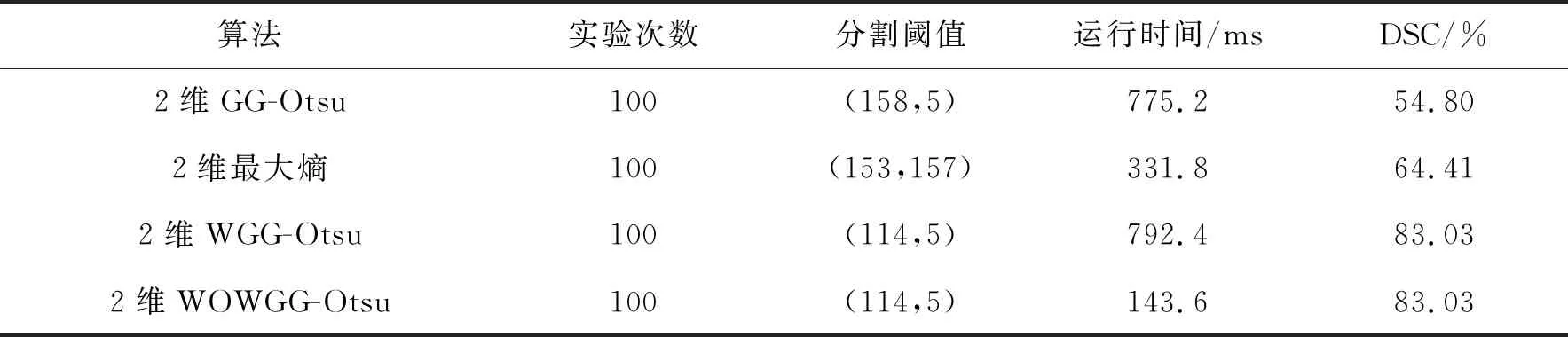
表2 4种算法对斑块缺陷图像的分割性能比较
从表2的分割阈值可知,相对于2维GG-Otsu算法及2维最大熵算法,2维WGG-Otsu算法及2维WOWGG-Otsu算法的分割精度高.从运行时间可知,2维WOWGG-Otsu算法的分割效率最高.
4种算法对钢板表面压入氧化铁皮缺陷图像的分割性能比较如表3所示.
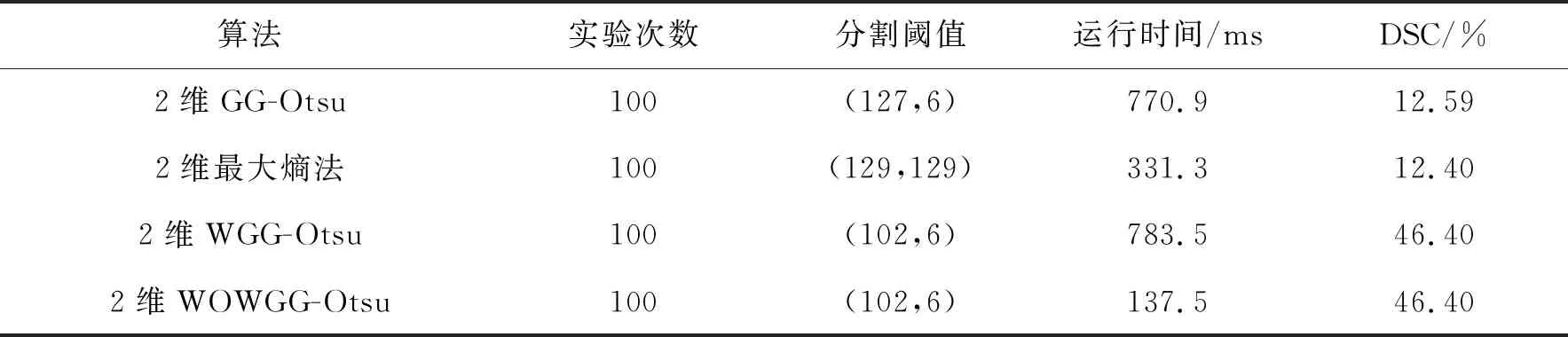
表3 4种算法对压入氧化铁皮缺陷图像的分割性能比较
从表3的分割阈值可知,相对于2维GG-Otsu算法及2维最大熵算法,2维WGG-Otsu算法及2维WOWGG-Otsu算法的分割精度高.从运行时间上可知,2维WOWGG-Otsu算法的分割效率最高.
4种算法对钢板表面划痕缺陷图像的分割性能比较如表4所示.
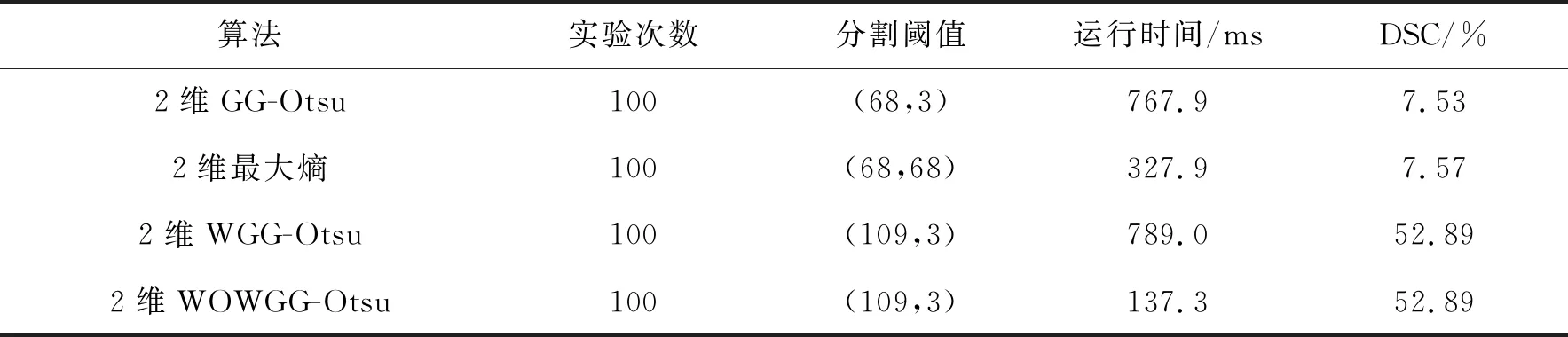
表4 4种算法对划痕缺陷图像的分割性能比较
从表4的分割阈值可知,相对于2维GG-Otsu算法及2维最大熵算法,2维WGG-Otsu算法及2维WOWGG-Otsu算法的分割精度高.从运行时间上可知,2维WOWGG-Otsu算法的分割效率最高.综上所述,可知4种算法中2维WOWGG-Otsu算法对夹杂、斑块、压入氧化铁皮和划痕4种缺陷图像的分割精度及效率均最高.
4 结束语
相对于2维GG-Otsu算法和2维最大熵算法,笔者提出的2维WGG-Otsu算法使得到的分割阈值更接近目标直方图与背景直方图间的波谷处的阈值,从而减少了外界噪声、背景与目标间的差异对分割的影响,提高了分割的精度.将2维WGG-Otsu算法与鲸鱼优化算法相结合,能快速找到最佳分割阈值,缩短了分割时间,从而提高了分割的效率.实验结果表明,相对于其他3种算法2维WOWGG-Otsu算法的分割精度及效率均最高,具有良好的应用前景.
