高超声速滑翔飞行器地形匹配辅助导航方法研究

鲜勇，任乐亮，杨子成，张大巧，李杰

（火箭军工程大学 作战保障学院，西安710025）

高超声速滑翔飞行器通常具有长航程、飞行速度快、突防能力强等特点，可靠且高精度的导航方式将会带来成倍的作战效能［1］。高超声速滑翔飞行器通常以惯性导航系统为主体，而由于惯性器件参数会随时间漂移，在复杂飞行条件下，长时间导航后将产生较大的导航误差，仅采用惯性导航将无法满足精度需求。惯性器件精度提高困难且付出成本高，而采用组合导航方式可以分担惯性器件压力［2］，提高导航精度。

相比于卫星导航系统而言，地形匹配辅助导航系统在可靠性方面更胜一筹［3］，具有较强的抗干扰能力和较好的隐蔽性，在合理设计地形匹配导航系统后，适合作为高超声速滑翔飞行器辅助导航方式。

地形匹配辅助导航方式在亚声速巡航导弹上成功应用，命中精度有大幅度提高［4］，有很多经验可以借鉴。但同时高超声速滑翔飞行器与亚声速巡航导弹有明显不同，如高超声速滑翔飞行器典型弹道方式为“钱学森弹道”和“桑格尔弹道”，飞行高度通常超过30 km［5］，飞行速度在5Ma以上，这些特点对地形匹配辅助导航系统相关仪器提出了更高的要求，并对应用地形匹配可行性提出了更大的挑战。传统的地形匹配辅助导航系统，主要靠雷达高度计和气压高度计获取弹下点地形高程序列［3］，而在30 km以上高度，大气极为稀薄［6］，气压高度计将无法正常使用（具体分析见第1节），为保证地形匹配辅助导航系统正常工作，亟待研究气压高度计失效时的替代方案，而相关研究较少。

惯性系统高度通道发散严重［7-9］，短时精度很高［10］，因此，文献［10］提出了一种无气压高度计的飞机地形匹配辅助导航方案，即由惯性系统提供绝对高度信息，但没有对该方案深入研究，缺少对该方案适应性的分析。同时，高超声速滑翔飞行器与飞机有很大不同，需要结合其弹道特点对可行性进行分析。文献［11-16］对高超声速滑翔飞行器典型弹道进行了较为深入的研究，文献［11-12］考虑地球自转影响，建立了完整的动力学方程，对滑翔弹道进行了优化设计；高精度滑翔弹道解析解在20世纪70年代以后成为研究重点［13］，通过解析解有助于研究滑翔弹道本质规律，文献［13-15］在平衡滑翔假设的基础上，推导了平衡滑翔弹道解析解，对速度、高度和速度倾角之间的关系进行了深入研究，其中，文献［14］进一步对跳跃滑翔弹道特性进行了分析。以上文献为本文研究提供了理论基础。

本文在上述研究成果的基础上，分析了2种气压高度计失效时的替代方案：等高飞行方案和基于惯性系统解算绝对高度方案。为对2种方案进行对比分析，首先，以CAV-H为研究对象，推导了高超声速滑翔飞行器高度变化量与时间的对应关系，分析了典型弹道短时高度变化规律；其次，结合典型弹道特点和捷联惯性导航系统（SINS）误差模型，建立了惯性系统高度通道短时稳定性解析模型。

1 问题分析与方案设计

气压高度计是地形辅助导航系统获取绝对高度的重要仪器［3］，其精度高低将直接影响地形匹配定位精度。高超声速滑翔飞行器弹道与亚声速巡航导弹弹道有明显区别，飞行高度在30 km以上，速度在5Ma以上，这些特点将严重影响传统的气压高度计工作状态。

气压高度计误差可以分为模型误差和传感器测量误差两方面［17-18］。模型误差是由于真实大气模型与标准大气模型不同，造成的测量误差，在测量位置变化不大的情况下，可以认为是常值误差［17］。传感器测量误差主要是压力传感器受到自身器件精度以及受到外界干扰等影响［19-20］，引起测量得到的外界大气压力存在一定的噪声，该部分为动态误差。而在30 km以上高度，传感器测量误差较大。

压力传感器测量范围将决定气压高度计工作范围，而目前电子式气压高度计使用范围在低层大气，如精度较高的BMP180［21］、BMP388［22］型气压高度计最大测量高度为9 km，FA-AP-0002［17］型气压高度计最大测量高度为10 km，远低于高超声速滑翔飞行器滑翔飞行高度。同时，压力传感器分辨率将决定最小可分辨高度差，图1给出了高度h处压强差1 Pa对应的高度差ΔH，可以看出，在40 km以上，1Pa的压强差对应的高度差已经达到了26 m。而1 Pa的分辨率已经达到了目前传感器正常工作时的极限，芬兰VAISALA公司的PTB210气压高度计分辨率在5.6 Pa左右［23］，BMP180超高分辨率下噪声的均方根为2 Pa，BMP388最高分辨率大约为1.2 Pa，MS5611-BA01高分辨率下噪声的均方根为1.5 Pa［24］。随着高度的增大，压力传感器分辨率还会降低［25］。

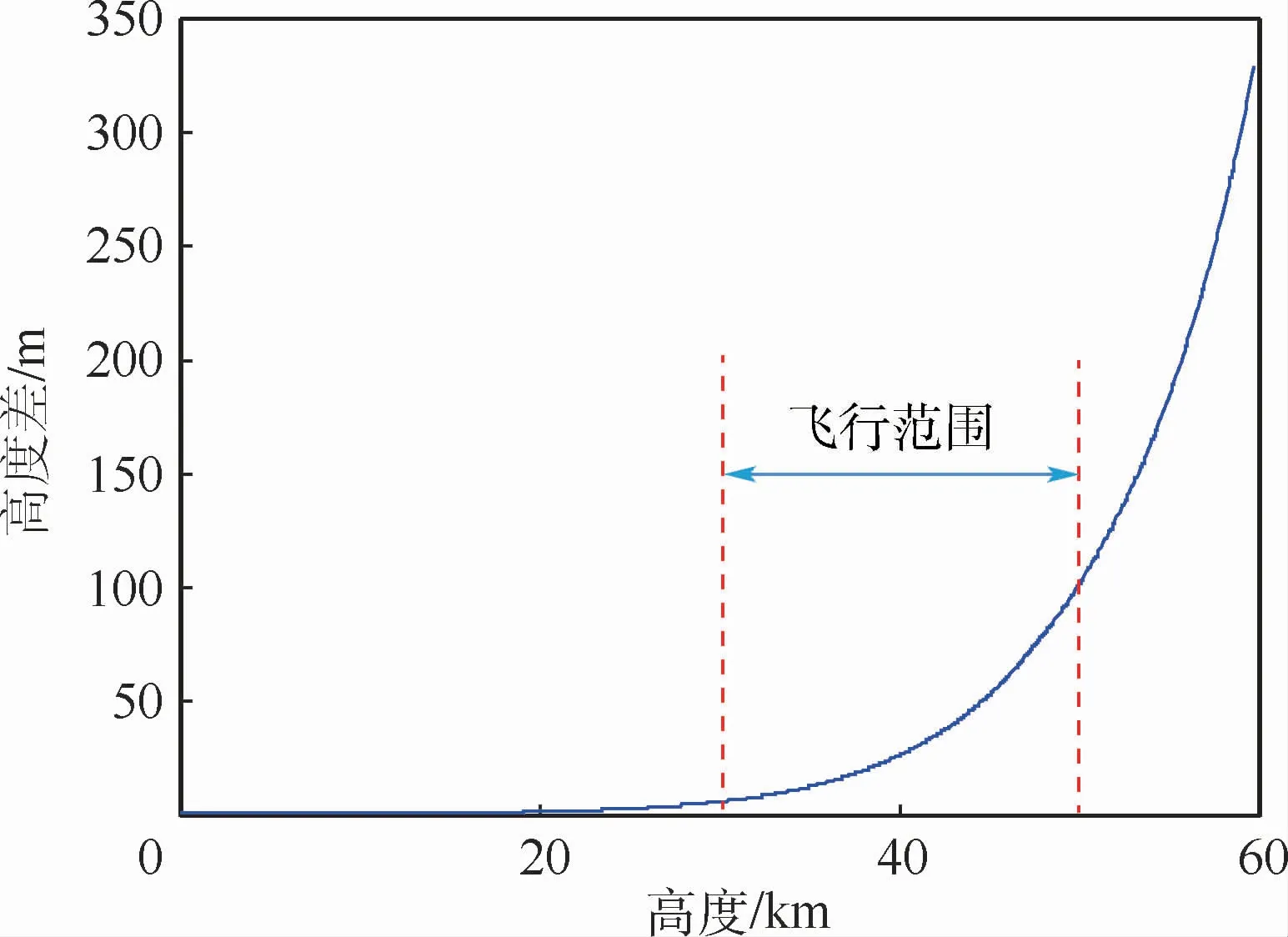
图1 高度h处压强差1 Pa对应的高度差Fig.1 Height difference corresponding to pressure difference of 1 Pa at h height

基于上述分析，在30 km以上高度，传统的气压高度计将无法精确测量绝对高度［20，26］，因此，需要研究可以代替气压高度计的方案，支持高超声速滑翔飞行器在滑翔飞行段完成地形匹配。一种思路是，增加其他高度测量的仪器测量绝对高度，如引力高度表［26］，但是文献［26］指出，这需要极高灵敏度的引力敏感元件，技术水平还未达到；另外一种思路是，在现有测量仪器基础上，结合飞行器弹道以及匹配算法，探索无气压高度计辅助的可行方案。本文基于均方差（MSD）算法对第2种思路进行研究，由MSD算法［3］可得

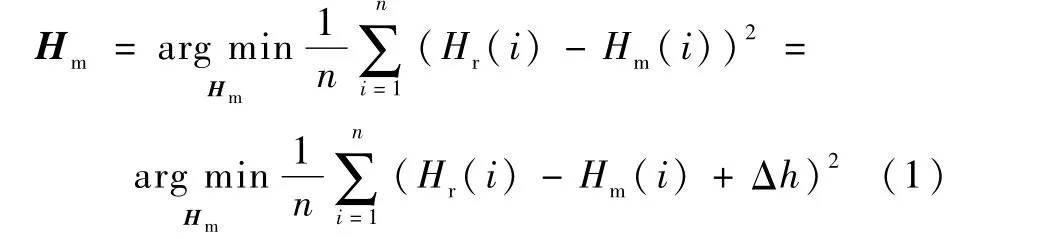
式中：Hm为匹配算法得到的弹下点位置对应的数字地图上的高程序列；Hr为实测高程序列；n为高程序列长度；Δh为常值。

由式（1）可知，实测数据的常值误差对MSD算法精度没有影响。基于此结论，本文对以下2个替代方案进行了分析。

1）等高飞行方案。滑翔段弹道在高程方向起伏较小，在误差允许范围内，短时间内近似为在H高度等高飞行，因此，可以将H认为是实测高程常值误差，仅采用雷达高度计提供的相对高度，即可完成地形匹配。

2）基于惯性系统解算绝对高度方案。可以将惯性导航高度误差看作两部分：一是进入匹配区时的初始导航误差，由长时间导航误差累积得到，该误差项较大；二是在地形匹配区内的短时导航误差，该误差项很小。因此惯性导航高度误差可表示为一个常值系统误差与一个动态误差之和，而MSD算法对系统误差不敏感，因此，当动态误差在允许范围内时，可以代替气压高度计。

2 等高飞行方案

2.1 平衡滑翔条件下高度变化量分析

根据式（9）可以得到平衡滑翔条件下t时刻高度变化量。

1）取ΔT＝1 s，假定初始高度为60 km，升力系数为0.9，升阻比取不同值。高超声速滑翔飞行器飞行2 000 s时，射程已经可以达到10 000 km［14］，因此，以2 000 s为飞行时间上界，得到不同升阻比下δh随时间变化曲线，如图2所示，并记录2 000 s时的δh得到表1。

可以看出，平衡滑翔状态下，同一初始高度，升阻比越小，δh越大，δh与阻力系数紧密相关。

2）取ΔT＝1 s，假定升力系数为0.63，升阻比为3.2，得到不同初始高度H0下δh随时间变化曲线，如图3所示，并记录2000 s时的δh得到表2。

可以看出，同一迎角下（近似为升阻力系数相同），在不同初始高度达到平衡滑翔条件，δh不同，初始高度越小，δh越大。

基于1）和2）的分析，可以得到平衡滑翔状态下，δh在特定飞行条件下较小，可以简化为等高飞行，但会对滑翔段弹道规划带来极大的约束，工程可行性较小，考虑飞行器控制误差后，可行性将进一步下降。

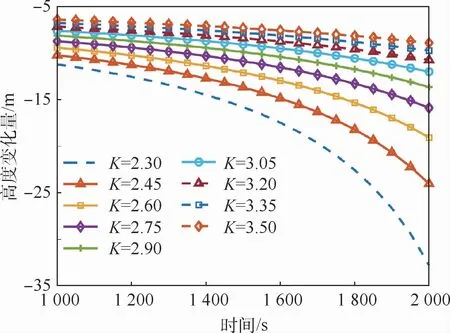
图2 不同升阻比下δh随时间变化曲线Fig.2 Variation curves ofδh with time under different lift-drag ratios

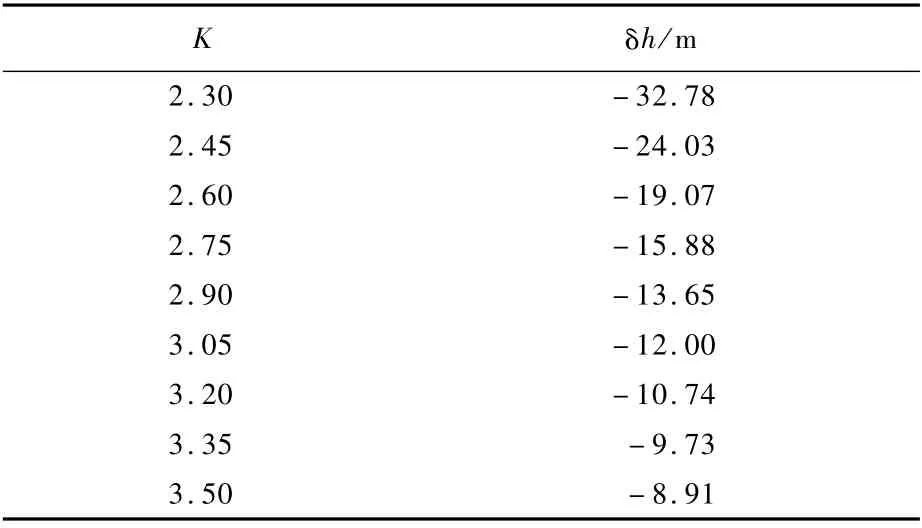
表1 不同升阻比下2000 s时的δhTable 1 δh at 2 000 s w ith different lift-d rag ratios

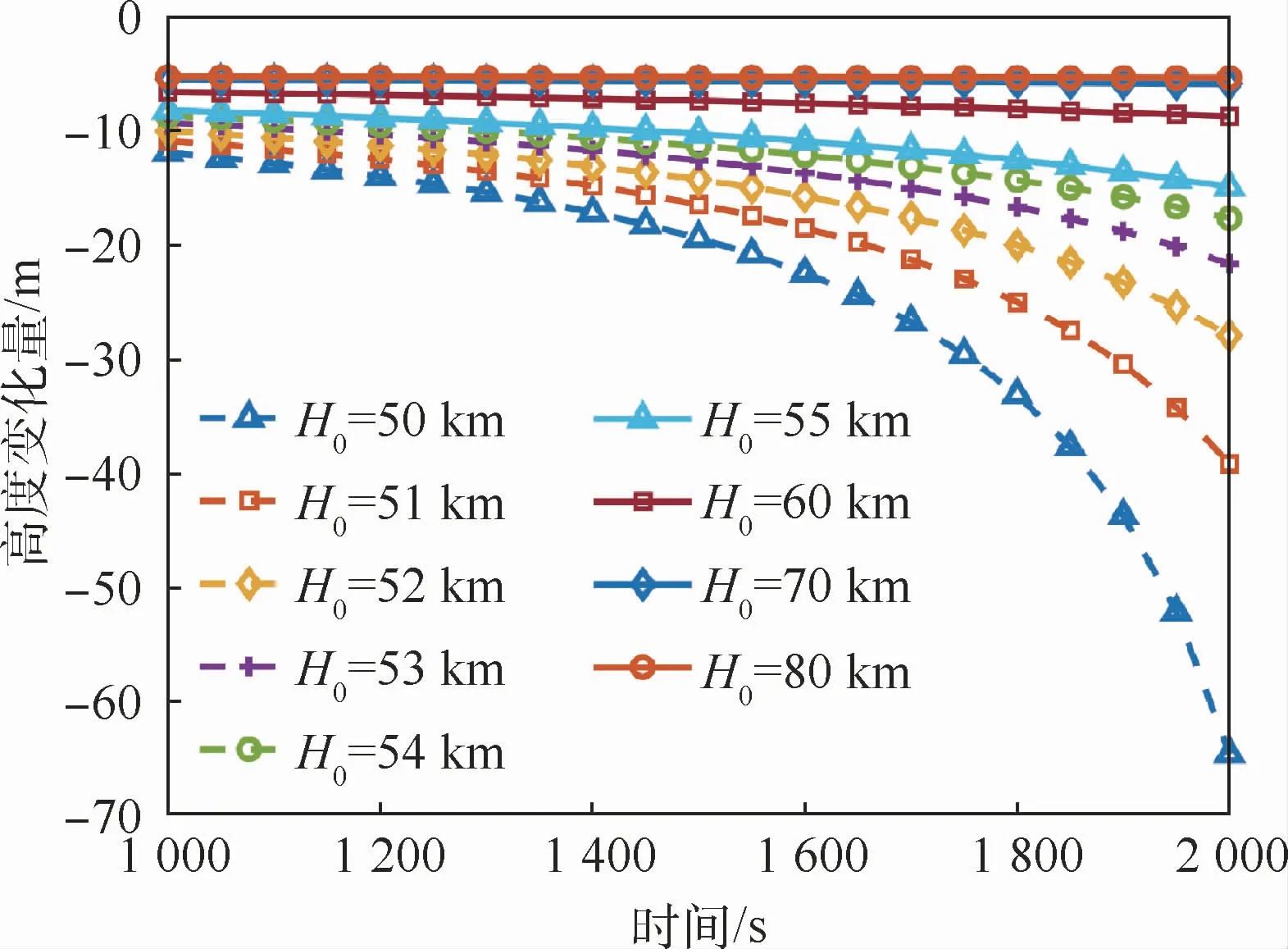
图3 不同初始高度下δh随时间变化曲线Fig.3 Variation curves ofδh with time under different initial heights

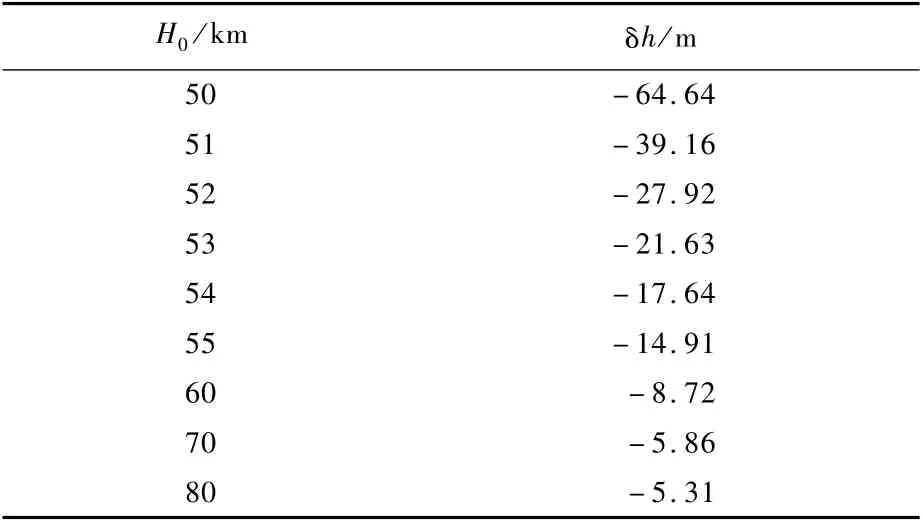
表2 不同初始高度下2 000 s时的δhTab le 2 δh at 2000 s w ith different initial heights

2.2 跳跃滑翔条件下高度变化量分析

将平衡滑翔状态下速度、高度、速度倾角分别记为VEG、HEG和ΘEG，单独改变初始速度V0、初始高度H0、初始速度倾角Θ0，得到跳跃滑翔弹道［14］如图4～图7所示。

由图4可以看出，跳跃滑翔状态下高度变化曲线δhSG在平衡滑翔状态下高度变化曲线δhEG上下跳跃，随着时间的增加，δhSG趋于δhEG。进一步增大初始速度偏差，得到图5。可以看出，初始状态改变量越大，跳跃程度越大。

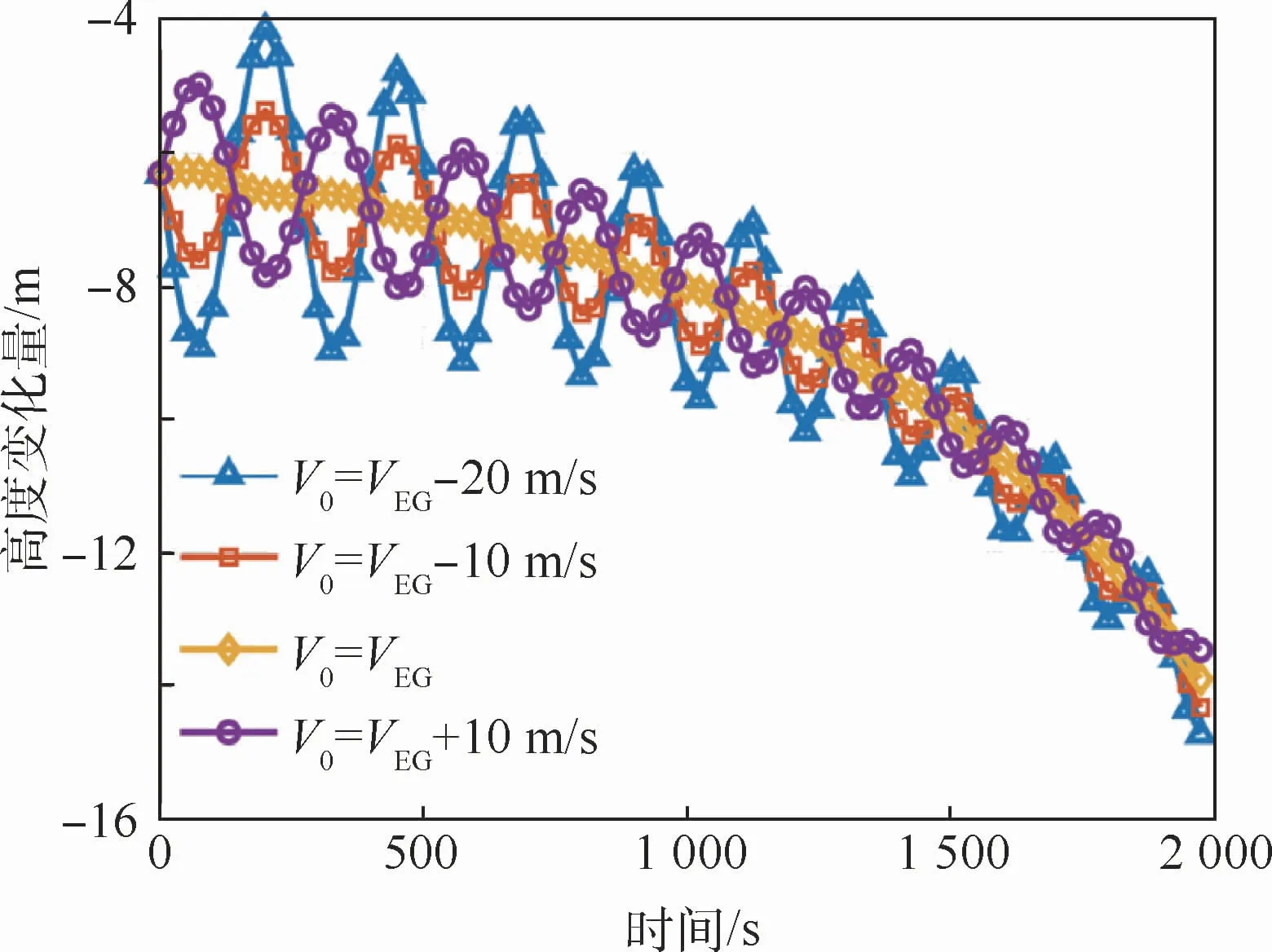
图4 较小初始速度偏差下δh随时间变化曲线Fig.4 Variation curves ofδh with time under smaller initial velocity deviation

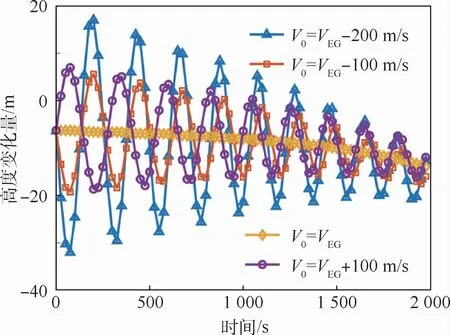
图5 较大初始速度偏差下δh随时间变化曲线Fig.5 Variation curves ofδh with time under larger initial velocity deviation

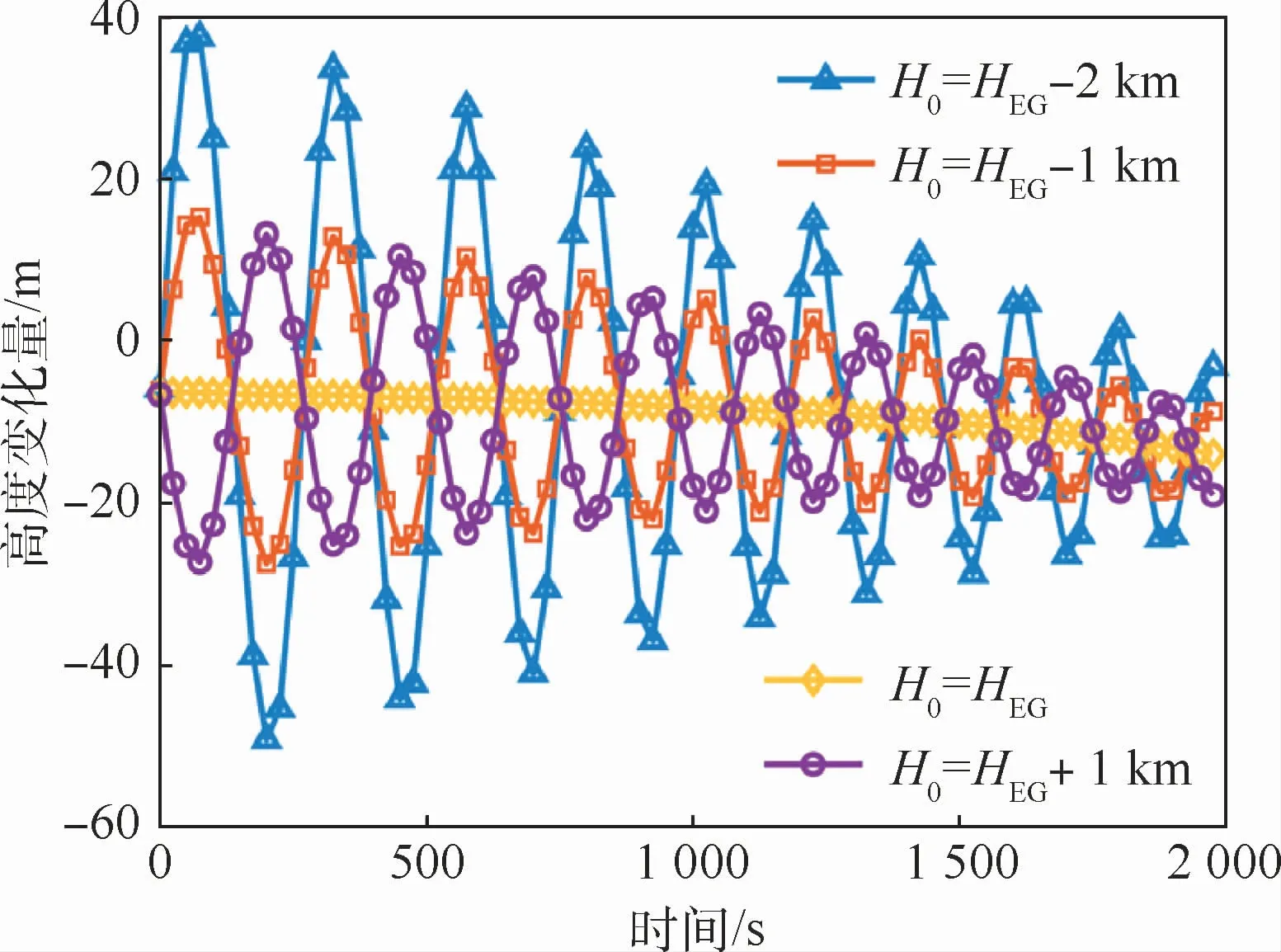
图6 不同初始高度偏差下δh随时间变化曲线Fig.6 Variation curves ofδh with time under different initial height deviations

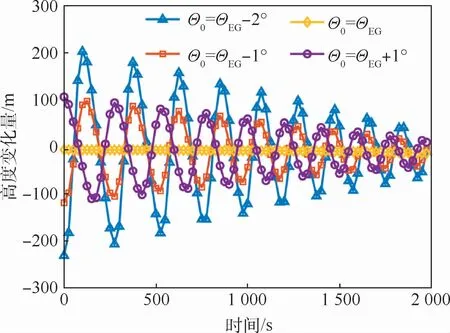
图7 不同初始速度倾角偏差下δh随时间变化曲线Fig.7 Variation curves ofδh with time under different initial flight path angle deviations

图6和图7分别给出了单独改变初始高度以及单独改变初始速度倾角情况，由对应的δhSG曲线可以看出，其变化规律与单独改变初始速度情况类似。

在初始速度倾角偏差为－2°时，δhSG可以达到200m，将无法简化为等高飞行。因此，在跳跃滑翔状态下，会出现δhSG较大的情况，在滑翔飞行前期尤为明显，同时，存在δhSG较小的时刻，但这会给地形匹配区选取带来极大的困难，而且考虑飞行器控制误差后，可行性将进一步降低。

3 基于惯性系统解算绝对高度方案

3.1 惯性系统高度通道短时稳定性解析模型

为方便分析，建立如图8所示的坐标系，坐标原点为飞行器质心O，Oxm沿飞行方向、平行于发射惯性坐标系xy平面且与当地水平面平行，Oym轴过地心且指向天，Ozm与Oxm、Oym构成右手直角坐标系，以下简称m系。图8中，Oe为地心，ω为地球自转角速度矢量，φm为飞行器纵对称轴Ox1与xmOym平面的投影与Oxm轴夹角，在Oxm轴之上为正。

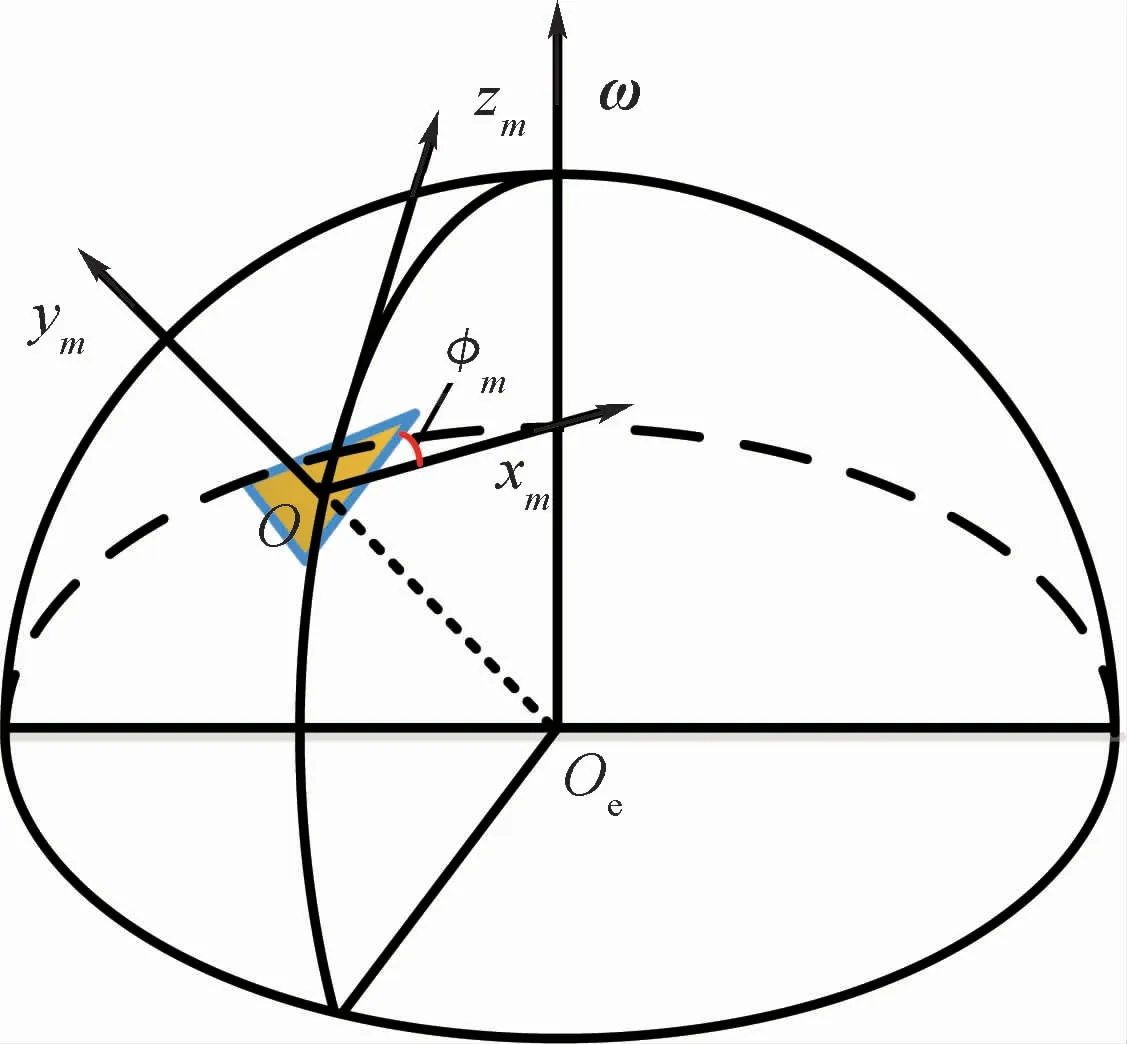
图8 本文定义的m坐标系Fig.8 m coordinate system defined in this paper

根据平衡滑翔条件，作如下假设：

1）滑翔段当地弹道速度倾角很小，即Θ≈0。

2）根据滑翔段弹道特点，飞行器飞行速度快，气动外形升阻比大，平衡滑翔状态下，升力、离心力与引力平衡，Oym方向视加速度要小于1g0（g0为当地重力加速度），Oxm方向视加速度很小。为得到惯性系统解算绝对绝对高度在短时间内漂移量的上界值，进一步假设Oym方向视加速度等于1g0。

3）不考虑飞行器横向机动和地球自转，仅对纵向飞行弹道进行分析，即不考虑惯性系统误差情况下，飞行器在发射惯性坐标系xOy平面飞行。

4）考虑到飞行器采用激光捷联惯性导航方式，滑翔段高度通道发散情况与飞行过程中的迎角紧密相关。为分析发散情况，进一步假设以常值迎角进行飞行。

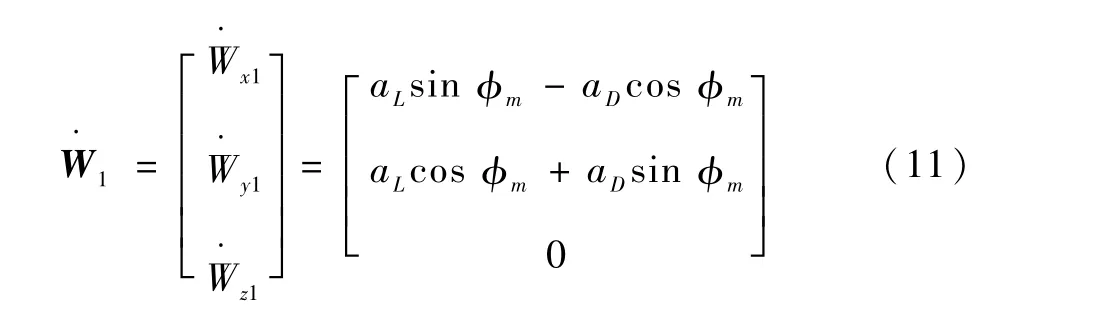
陀螺仪引起的视加速度偏差为

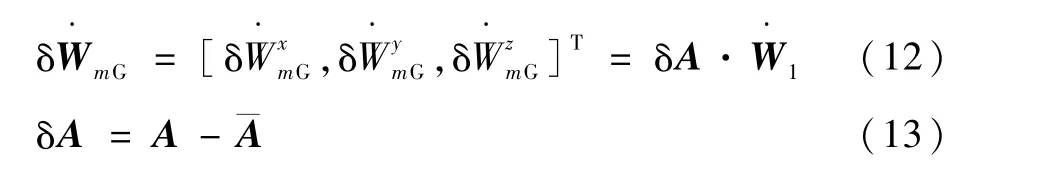
式中：A和¯A分别为存在陀螺仪误差和不存在陀螺仪误差弹体坐标系到m系的旋转矩阵；δA为旋转矩阵偏差，旋转矩阵A为

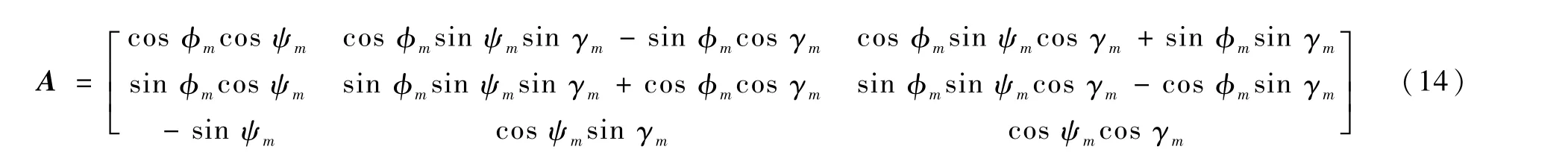
式中：ψm、γm为m系与弹体坐标系之间的夹角；ψm为Ox1与xmOym平面之间的夹角，顺Oxm轴看去，偏左为正；γm为飞行器横轴Oz1与x1Ozm平面之间的夹角，在x1Ozm平面之下为正。

在整个飞行过程中陀螺漂移量并不大，故ψm和γm均为小量，略去二阶小量得

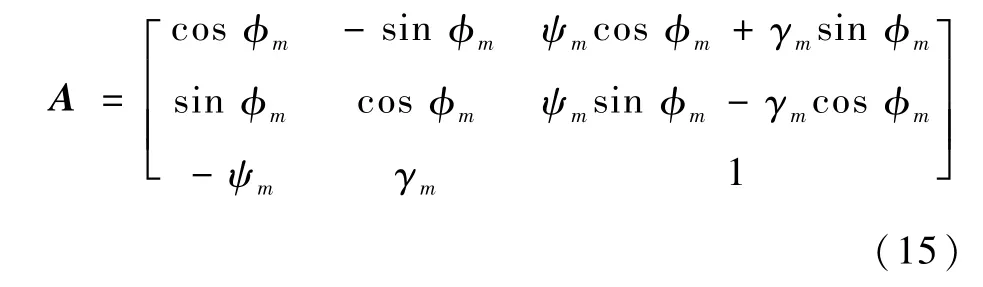
由文献［28］可得弹体坐标系各轴相对m系的旋转角速度ωx1、ωy1、ωz1与φm、ψm、γm欧拉角速度之间的关系为

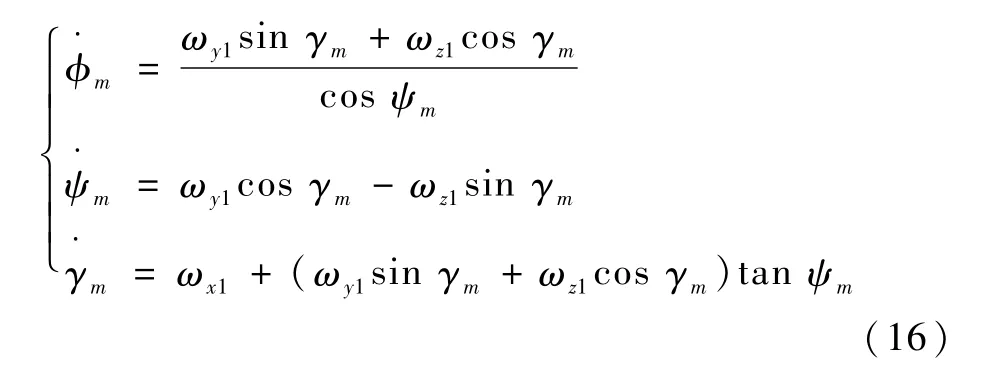
略去二阶小量后

在无陀螺仪测量误差情况下，ωx1、ωy1、ωz1均为0，考虑陀螺仪误差时，采用文献［27］中的误差模型可得

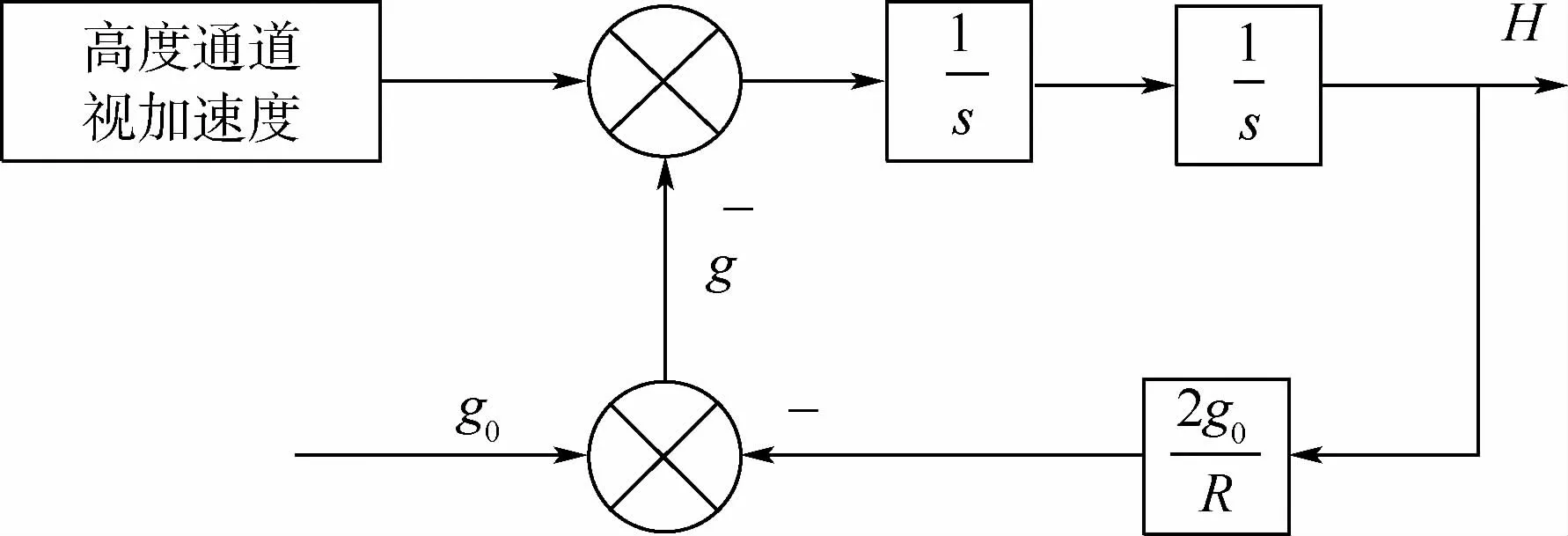
图9 高度通道方块图［7］Fig.9 Block diagram of height channels［7］

将式（25）代入式（26），可得

将式（28）进行拉普拉斯逆变换，合并同类项后得加速度计误差系数偏差紧密相关，因此，需要对纯惯导情况下，基于惯性系统解算绝对高度方案的适应性进行分析。

3.2 惯性系统高度通道短时稳定性影响因素

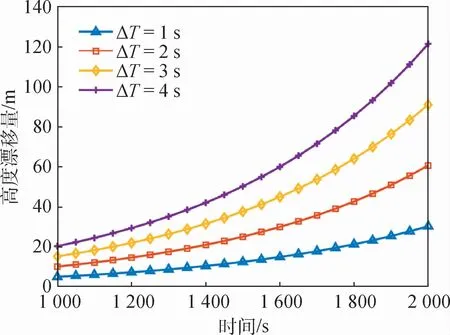
图10 不同ΔT下δh随时间t0 的变化曲线Fig.10 Variation curves ofδh with time t0 under differentΔT

表3 ΔT＝1 s时δh的大小Table 3 Value ofδh whenΔT＝1 s

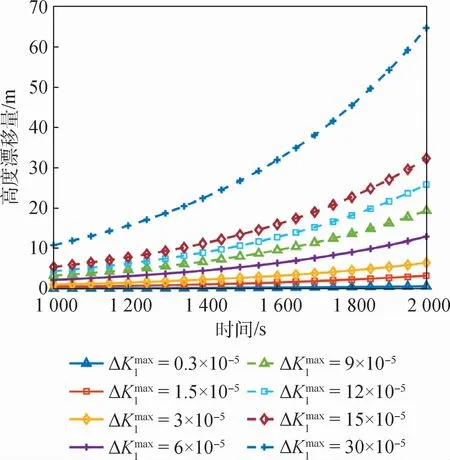
图11 不同加速度计误差系数偏差下δh随时间t0 的变化曲线Fig.11 Variation curves ofδh with time t0 with different deviations of accelerometer error coefficient

表4 不同加速度计误差系数偏差下t0 ＝2 000 s时δh的大小Tab le 4 Value ofδh when t0 ＝2 000 s w ith differen t deviations of accelerom eter error coefficient

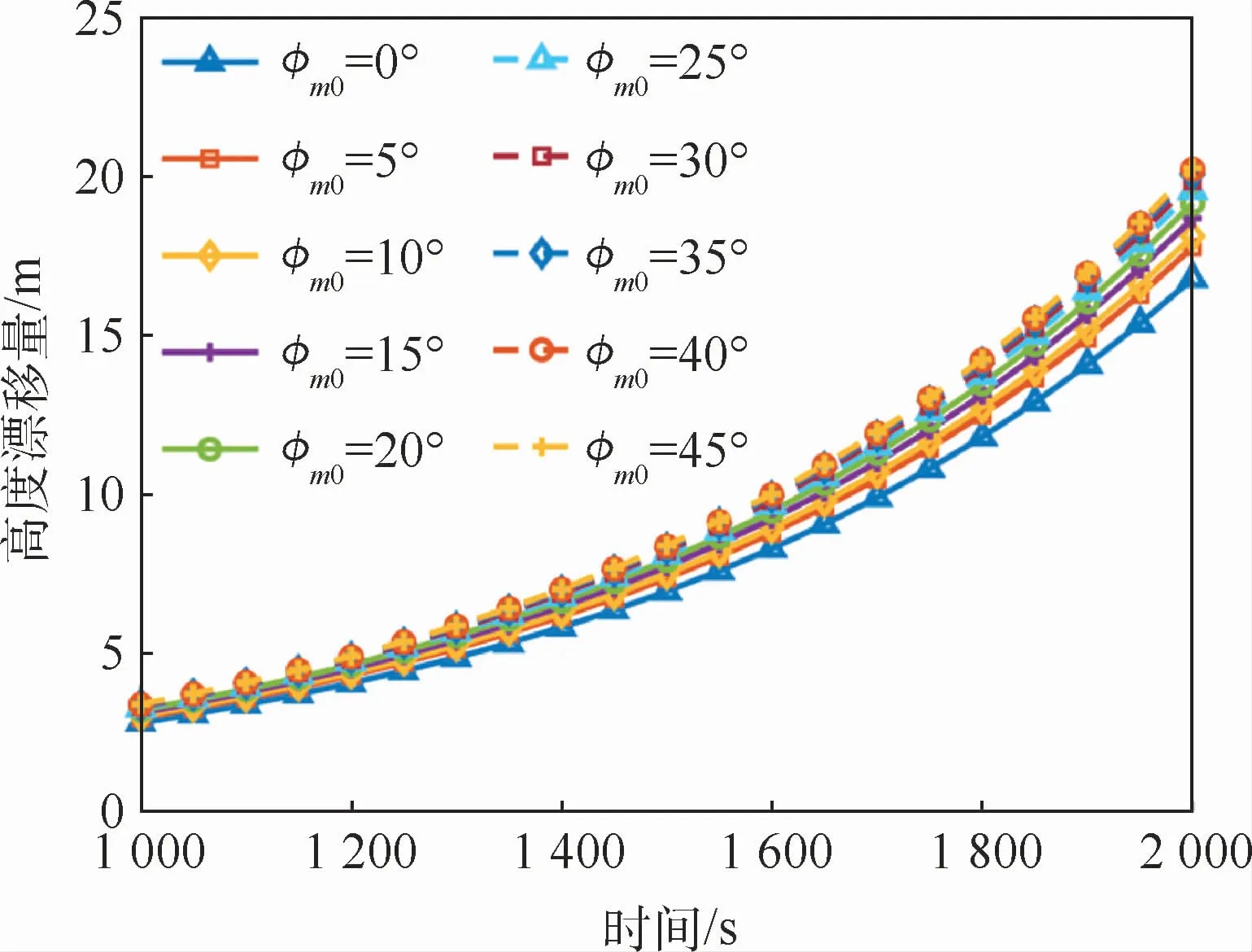
图12 不同φm0下δh随时间t0 的变化曲线Fig.12 Variation curves ofδh with time t0 under differentφm0

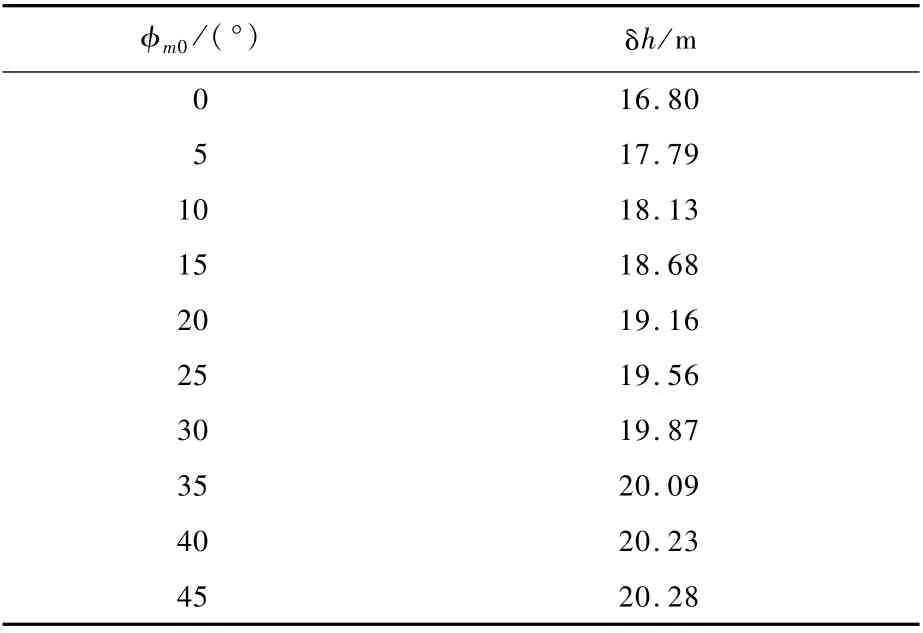
表5 不同φm0下t0 ＝2 000 s时δh的大小Table 5 Value ofδh when t0＝2000 s w ith differentφm0

4 仿真分析

以美国CAV-H为仿真对象，相关参数见文献［30］。为检验基于惯性系统解算绝对高度方案中简化模型的精度，考虑到实际飞行过程中视加速度是不断变化的，因此，不加入加速度计一次项偏差，设定仿真条件如下：ΔD0x＝ΔD0y＝ΔD0z＝0.03（°）／h，ΔK0x＝ΔK0y＝ΔK0z＝9×10－5g0，初始滑翔高度为55 km，根据文献［10］得到对应平衡滑翔初始速度为6 449.19 m／s，速度倾角为－0.05605°，飞行器保持15°迎角进行大升阻比飞行，φm0＝15°。根据动力学模型和惯性系统解算模型得到1 s高度漂移量δh1，弹道积分解算过程考虑柯氏力和牵连惯性力，由式（33）得到简化模型求解的1 s高度漂移量δh2。图13给出了δh1和δh2在2 000 s内大小关系。可以看出，两者差别很小，最大偏差为1.38 m，说明简化模型具有较高的精度，能够对该方案的适应性进行有效分析。该偏差与弹道跳跃程度有关系，速度倾角越小，该偏差越小。

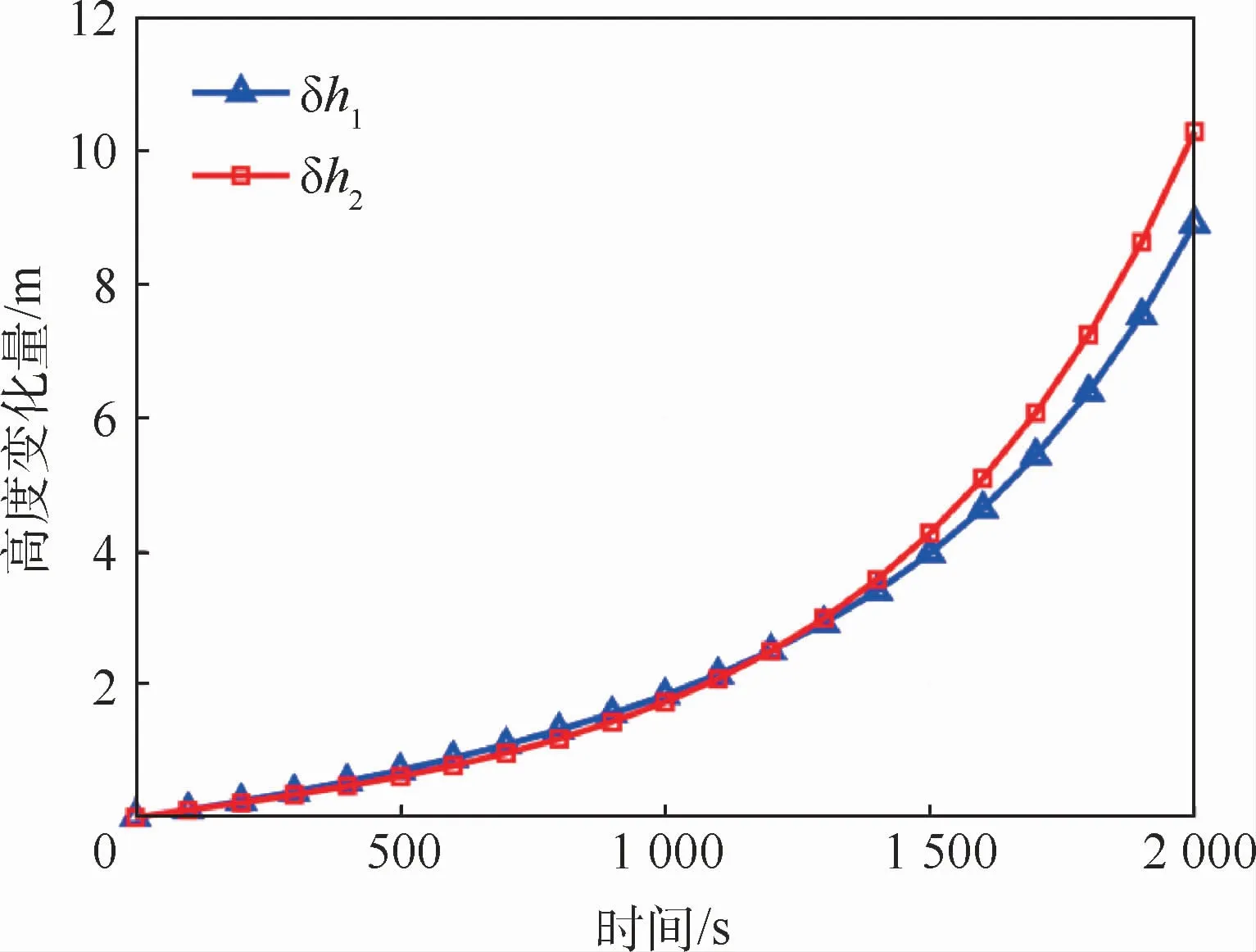
图13 δh1 和δh2 随时间变化曲线Fig.13 Variation curves ofδh1 andδh2 with time

在此基础上，加入加速度计一次项偏差，仿真条件设定如表6所示，采用蒙特卡罗法仿真5 000次，图14给出了滑翔飞行2 000 s过程中高度方向过载以及飞行高度随时间的变化曲线。

每隔100 s计算一次该时刻对应的δh，并统计5000次仿真中t0时刻δh的平均值、最大值、最小值以及标准差，得到图15。可以看出，δh在t0时刻的平均值基本为0，随着飞行时间的增加，δh的最大值不断增大，2 000 s时达到了10.52m，小于通过简化模型得到的上界值18.87m。结合图14可知，造成2种方法结果有差异的主要原因是：飞行器高度方向过载小于1g0。因此，实际飞行过程中δh将小于简化模型推导出的结果，更加说明基于惯性系统解算绝对高度方案具有一定的工程可行性。

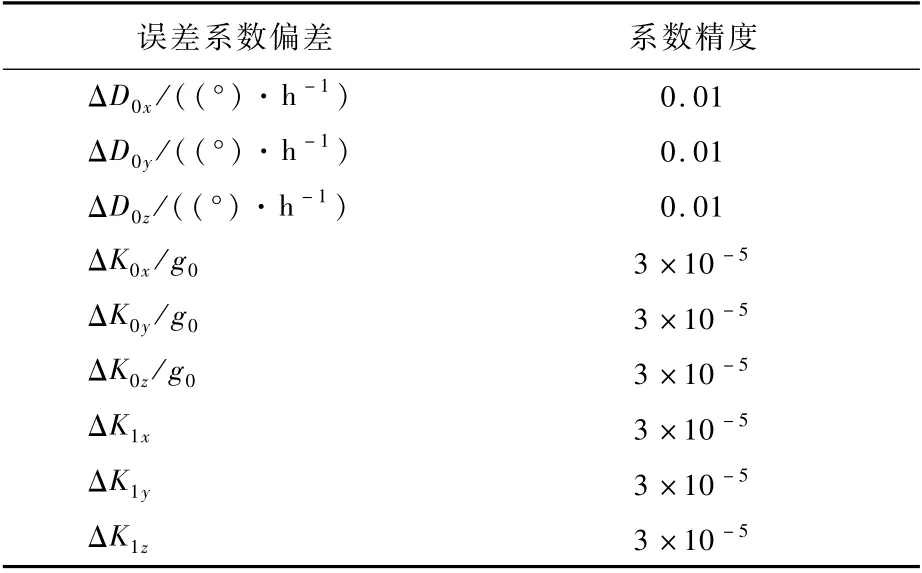
表6 工具误差系数精度Table 6 Instrum ental error coefficient accuracy

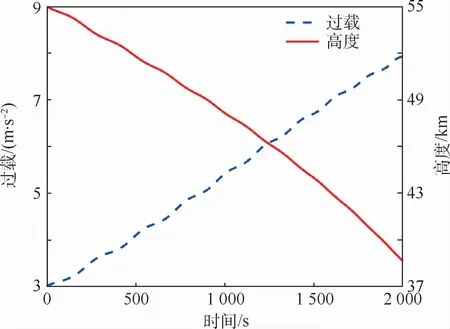
图14 过载和高度随时间变化曲线Fig.14 Variation curves of overload and height with time

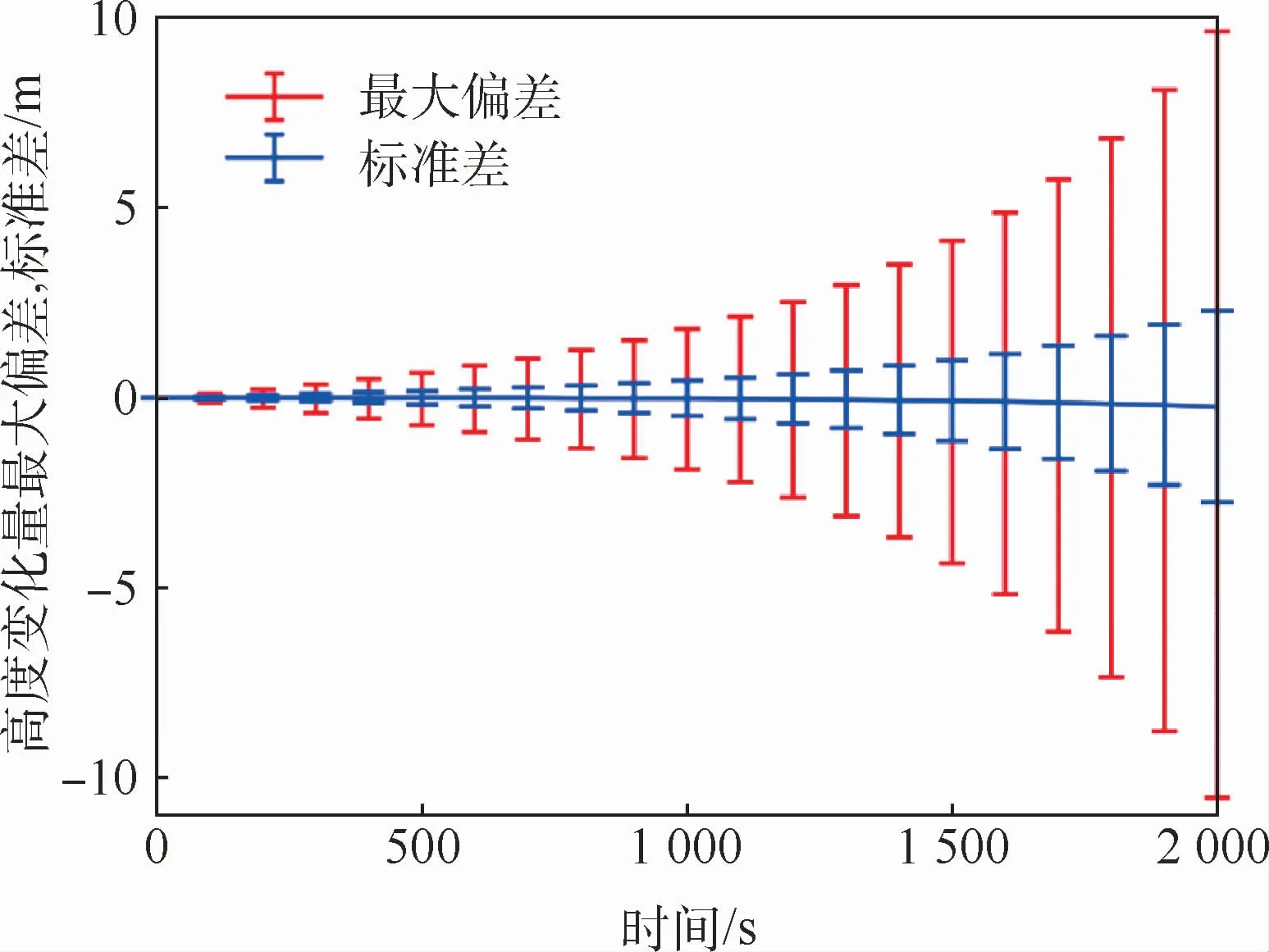
图15 δh随时间变化曲线Fig.15 Variation curves ofδh with time

5 结 论

针对气压高度计无法测量高超声速滑翔飞行器绝对高度问题，对比分析了2种代替方案：等高飞行方案和基于惯性系统解算绝对高度方案，得出：

1）针对平衡滑翔弹道，滑翔飞行2 000 s后，仅特定飞行条件下，单位时间内的高度变化量较小，可以简化为等高飞行，但会对滑翔段弹道规划带来极大的约束，工程可行性较小，且考虑飞行器控制误差后，可行性将进一步下降。

2）针对跳跃滑翔弹道，单位时间内的高度变化量与初始条件偏离平衡滑翔条件程度有关，当初始速度倾角偏差为－2°时，可以达到200m。同时，跳跃滑翔状态下的高度变化曲线围绕平衡滑翔状态下的高度变化曲线上下波动，存在高度变化量较小的时刻，但会极大压缩地形匹配区可选取范围，难以规划出合适的地形匹配区，且飞行器存在一定的控制误差，因此，工程可行性较小。

3）针对基于惯性系统解算绝对高度方案，高度变化量与惯性系统精度相关。在高超声速滑翔飞行器飞行2 000 s前提下，仅有陀螺误差（零次项系数偏差为0.01（°）／h）时，单位时间内高度变化量可忽略不计；再加入加速度计误差（零次项系数偏差为3×10－5g0）时，单位时间内高度变化量不超过10.52m，相对较小，能够满足地形匹配辅助导航系统精度要求，且具有一定的工程可行性。