推进剂贮箱区间干涉时变可靠性分析方法

2020-06-01辛腾达赵继广崔村燕段永胜

北京航空航天大学学报 2020年4期

辛腾达，赵继广，崔村燕，段永胜

推进剂贮箱作为贮存液体推进剂的大型薄壁结构，一旦发生泄漏将造成巨大的经济损失、环境破坏与人员伤亡，因此对推进剂贮箱的可靠性进行分析，对保证航天试验安全具有重大的现实意义。当火箭长期处于代发状态时，由于腐蚀、老化及外界随机载荷等因素的影响，推进剂贮箱的可靠性不再是传统模型下的单一数值，通常表现出时变特性。

结构时变可靠性分析主要基于跨越率的方法［1-2］，但由于其复杂的积分运算，很难在工程实际中进行有效的应用。为提高跨越率的计算效率，Andrieu-Renaud等［3］提出了PHI2方法。然而，对于一些复杂结构，PHI2方法的计算效率也将会大大降低。蒙特卡罗［4-5］、等效随机过程变换［6］、基于交叉熵的自适应采样［7］及应力-强度干涉［8］等基于概率随机过程的方法，也是时变可靠性分析中常用的方法。然而，概率可靠性分析在很大程度上依赖于参数的具体分布，如果由于缺乏数据而主观对分布形式进行假设，所得分析结果难以令人信服［9］。

20世纪90年代，Ben-Haim［10］首次提出基于凸模型理论的结构可靠度概念，将工程结构中的有界不确定参数表示为凸模型的形式。1995年，Elishakoff［11］将应力上界与屈服应力之比定义为非概率安全系数，应用区间理论对非概率安全性进行了分析。2001年，Guo和Lv［12］将不确定参数量化为区间变量，提出将原点到极限状态面的最短距离定义为非概率可靠度的方法。2003年，Qiu和Wang［13］将非概率区间方法与概率方法进行了比较，证明了区间理论与概率理论分析结果的一致性。近年来，非概率可靠性理论处理参数不确定问题的巨大优势，引起了理论界和工程界的广泛关注［14-15］，为推进剂贮箱时变可靠性分析提供了重要参考。

本文基于区间理论与应力-强度干涉理论，提出了一种应用于推进剂贮箱时变可靠性分析的非概率区间干涉时变可靠性分析方法，并结合推进剂贮箱示例参数，与服从正态分布的应力-强度干涉可靠性方法及区间可靠性方法进行了对比分析，验证了本文方法的有效性。

1 推进剂贮箱应力分析

1.1 椭球底圆柱贮箱模型

椭球底圆柱贮箱是贮存液体推进剂的重要结构，主要承受内部增压、轴压及液压的作用。根据椭球底圆柱贮箱的实际受力情况，建立椭球底圆柱贮箱模型，如图1所示。图中：xOy为基准坐标系，δb为椭球下底壁厚，r为参考点到y轴距离，b为椭球底高度，R1和R2分别为椭球下底第一曲率半径和第二曲率半径，φb为R2与y轴夹角，a为贮箱半径，δc为圆柱筒壁厚，hc为圆柱筒高度，h为推进剂液面高度，δr为椭球上底壁厚，R3和R4分别为椭球上底第一曲率半径和第二曲率半径，φr为R4与y轴夹角。

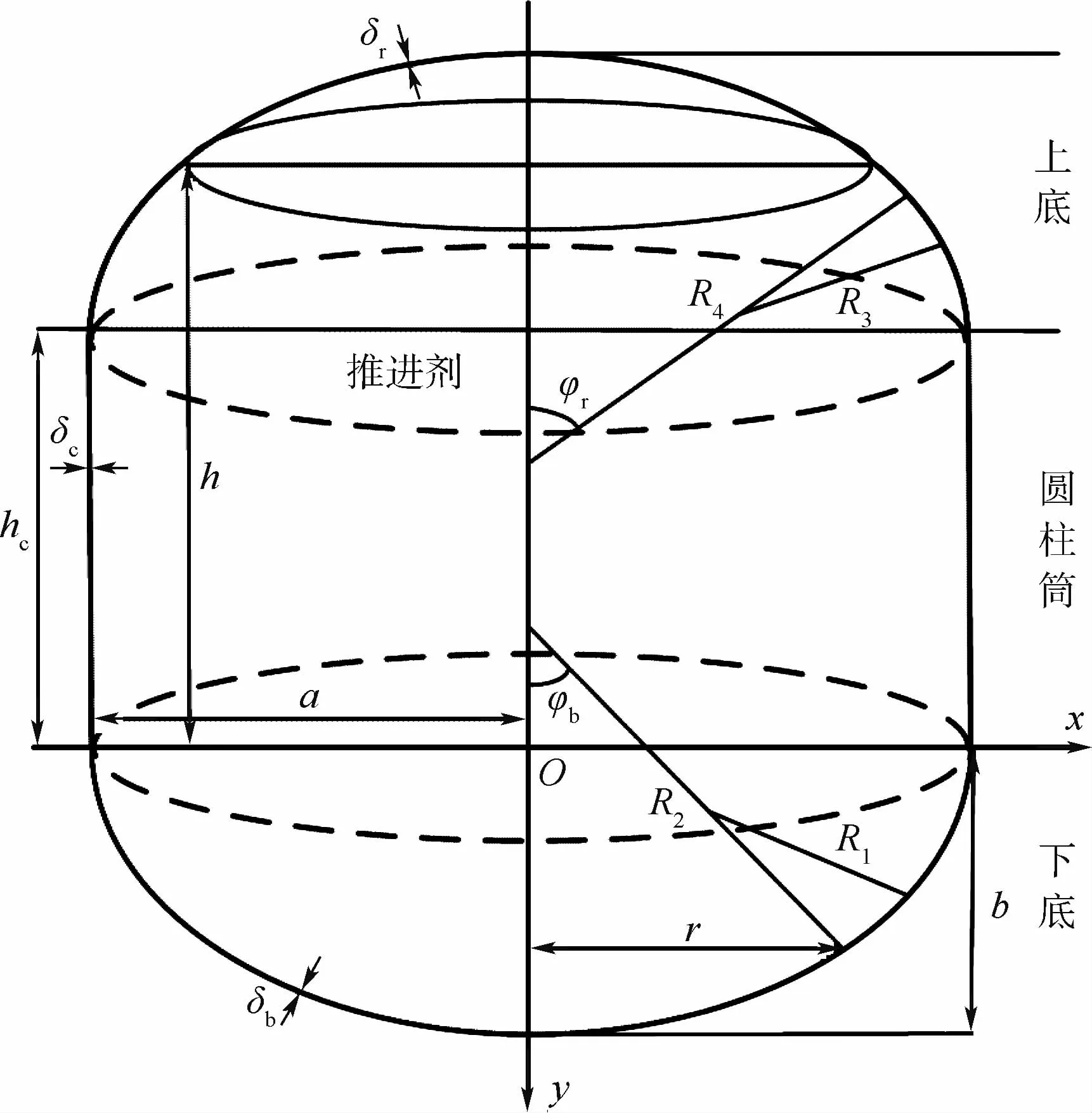
图1 椭球底圆柱贮箱模型Fig.1 Cylindrical tank model with ellipsoid bottom

1.2 椭球下底应力分析

据图1可知，贮箱椭球下底母线的椭圆方程可表示为

椭球模数m定义为贮箱半径a（椭球底母线长半轴）与椭球底高度b（椭球底母线短半轴）之比，即m＝a／b，可得

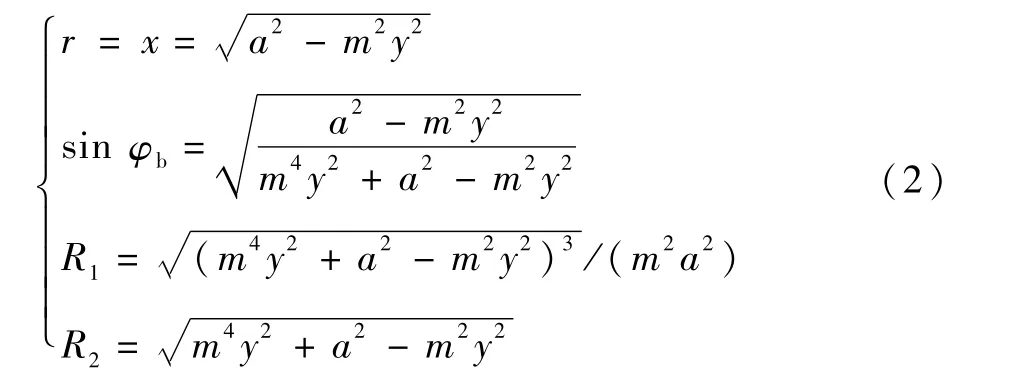
贮箱椭球下底主要承受内部增压与液压的作用，椭球下底参考面上的平衡方程可表示为

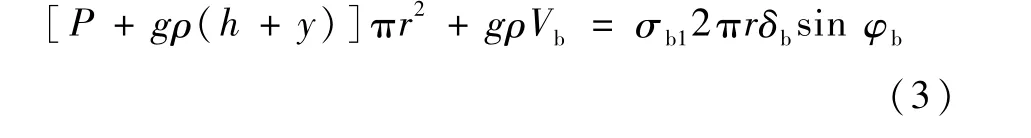
式中：P为内部增压；σb1为椭球下底经向应力；g为重力加速度，取为9.8m／s2；ρ为推进剂密度；Vb为参考面以下的容积，即

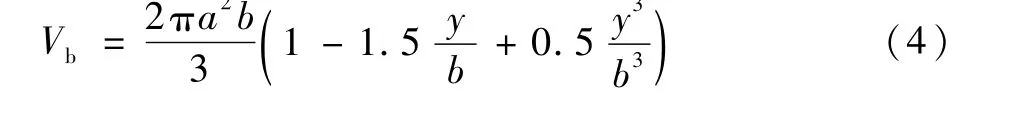
据式（3）可得椭球下底经向应力σb1为

根据旋转薄壳无矩理论，椭球下底任意微元均存在：

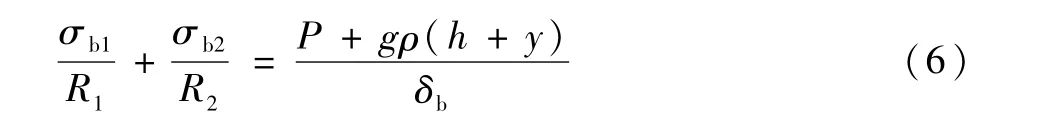
式中：σb2为椭球下底环向应力。

结合式（5）、式（6），可得

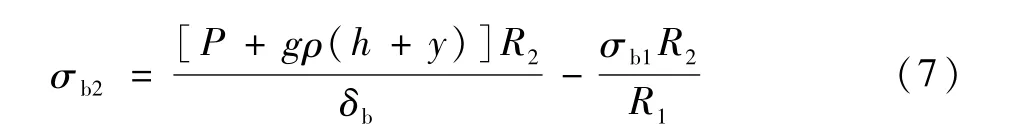
1.3 圆柱筒应力分析

在内部增压与轴压作用下，圆柱筒经向应力σc1为

式中：Z为火箭起飞质量。

在内部增压及推进剂液压的作用下，圆柱筒环向应力σc2为

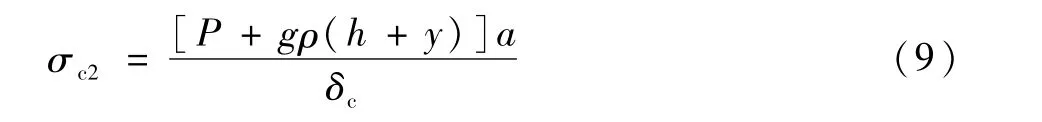
1.4 椭球上底应力分析

贮箱椭球上底（－hc－b≤y＜－hc）与椭球下底结构相同，即R3＝R1，R4＝R2，sinφr＝sinφb。

则贮箱椭球上底母线的椭圆方程为

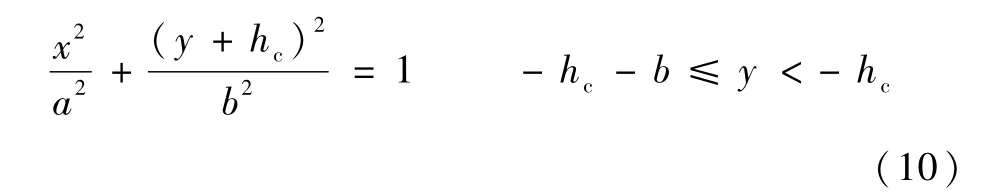
当－h≤y＜－hc时，椭球上底受内部增压与液压作用，椭球上底经向应力σr1与环向应力σr2分别为

1.5 贮箱等效应力分析

通过对贮箱各部分应力的分析，以σ1与σ2分别代表经向应力与环向应力，可知贮箱椭球下底、圆柱筒及椭球上底应力状态主要有3种形式：①σ1＞0与σ2＞0均为拉应力；②σ1≤0为压应力，σ2＞0为拉应力；③σ1＞0为拉应力，σ2≤0为压应力。

根据第三强度理论，等效应力σe可定义为［16］

2 区间干涉时变可靠性分析方法

设T为参考寿命，t∈［0，T］为服役时刻，X＝｛X1，X2，…，Xn｝为与强度R相关的参数集，Y＝｛Y1，Y2，…，Ym｝为与应力S相关的参数集，据应力-强度干涉理论，贮箱的状态函数可表示为基于Schaff幂指数强度退化模型［17］，服役周期内任意时刻贮箱强度可表示为

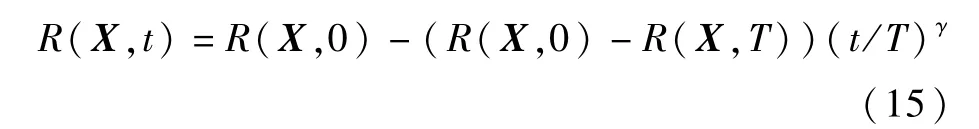
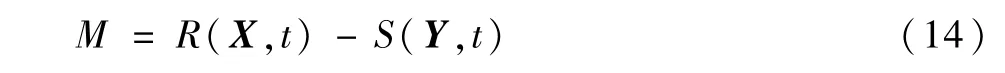
式中：R（X，t）为任意t时刻贮箱强度；R（X，0）为t＝0时刻贮箱强度；R（X，T）为t＝T时刻贮箱强度；γ为与材料相关的衰减系数。

根据区间理论，贮箱强度区间R（X，t）的上下界可分别表示为

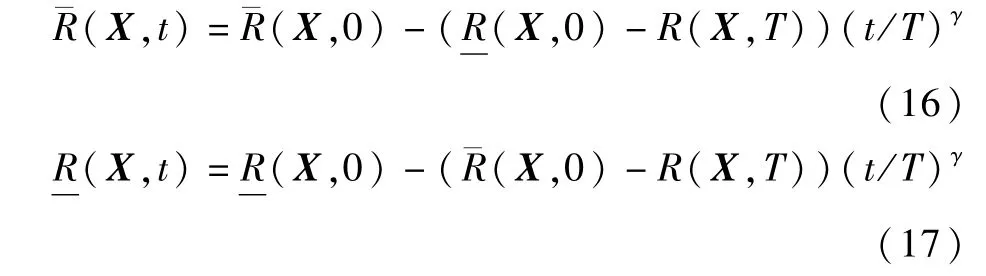
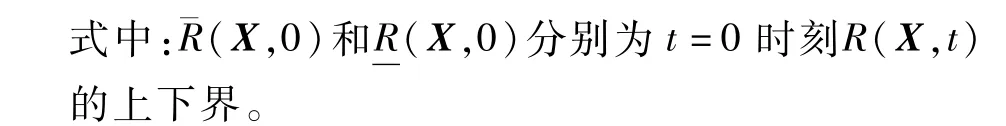
R（X，t）的中值与离差可分别表示为

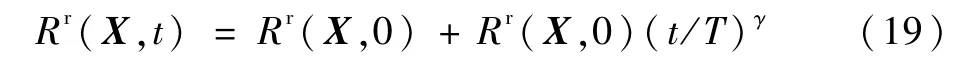
式中：Rc（X，0）和Rr（X，0）分别为t＝0时刻R（X，t）的中值与离差。

将贮箱常载荷应力Sn（Y，t）及不确定载荷应力Su（Y，t）表示为区间变量：

此时，将可靠域面积Ar与标准化区间面积A＝4的比值，定义为任意时刻区间干涉时变可靠性指标η：据式（31）可知η∈（0，1），贮箱处于非完全可靠状态，η表示结构的可靠度。当k＞1，k＝1或0≤k＜1时，任意时刻区间干涉时变可靠性指标η可据式（31）求得。以k＝2，k＝1及k＝1／2为例，随M＝0与标准化区间位置关系的变化，相应的η值如图3所示。

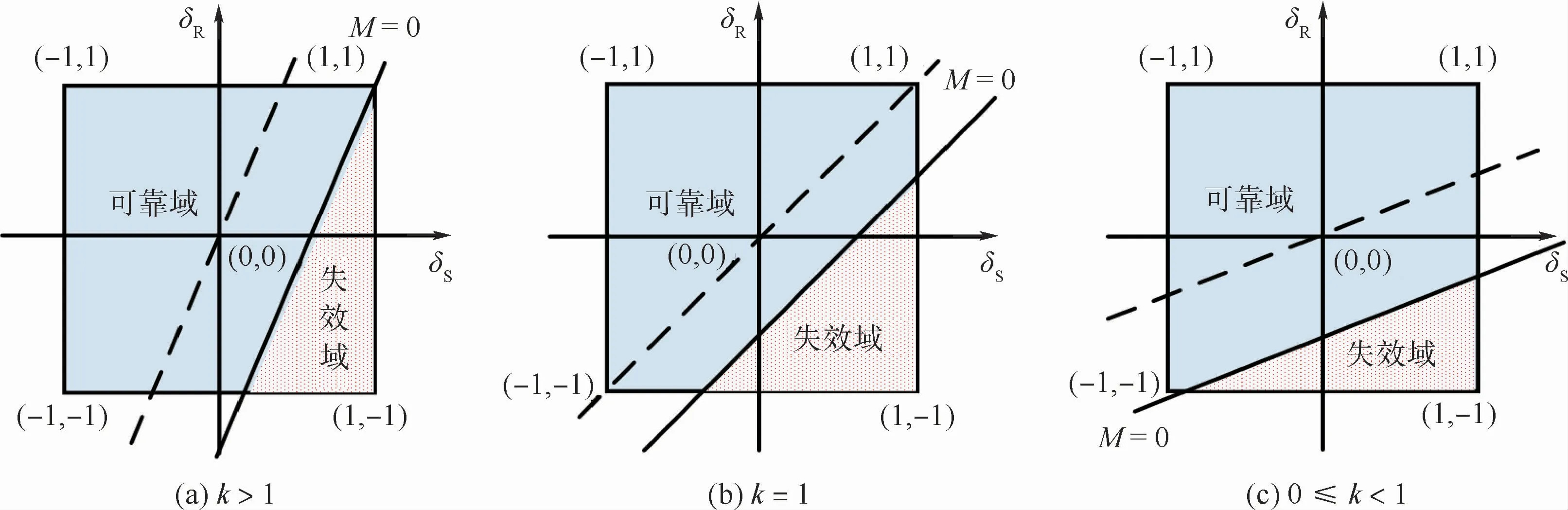
图2 临界状态函数与标准化区间Fig.2 Critical state function and normalized interval

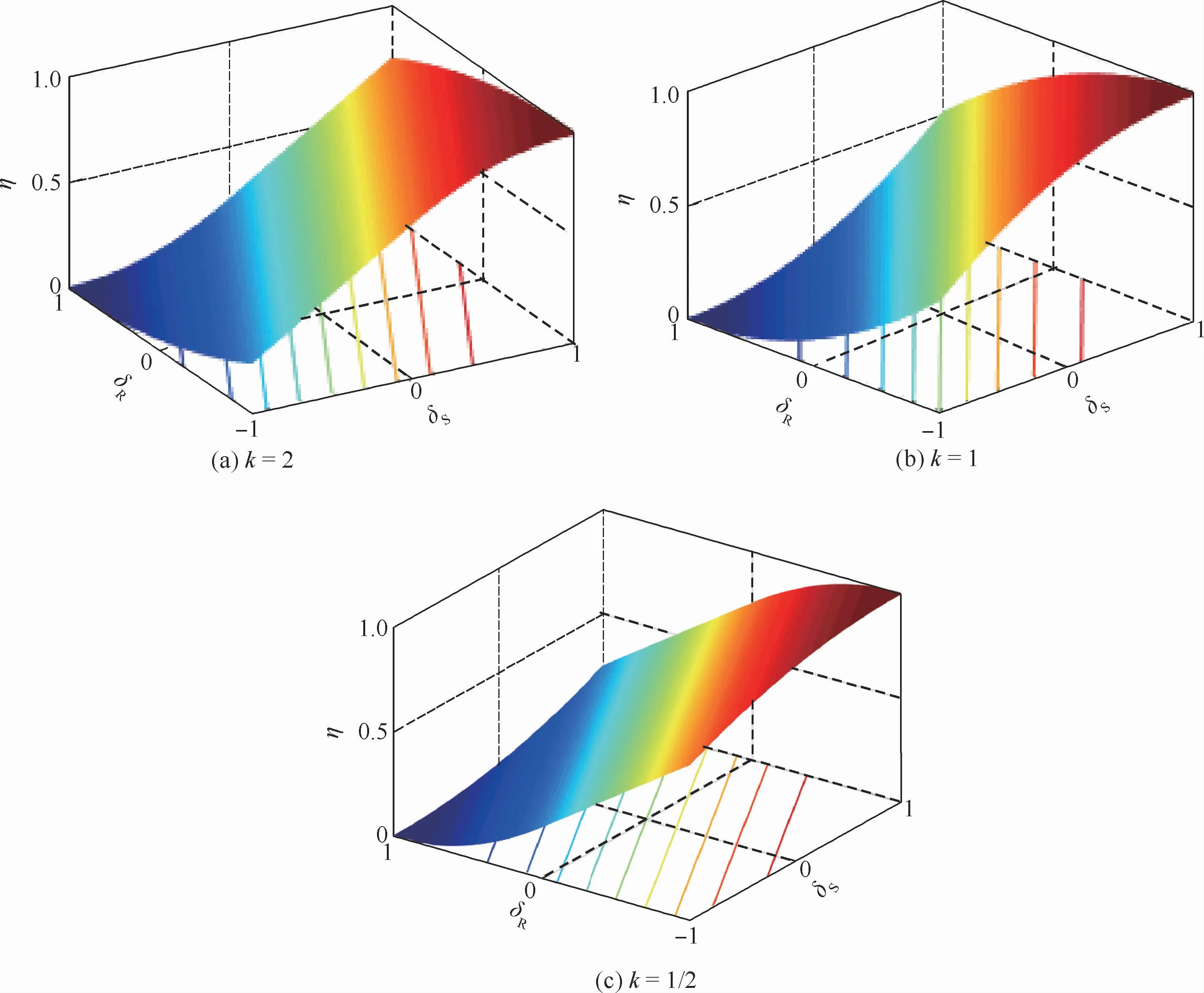
图3 k＝2，k＝1，k＝1／2时可靠性指标Fig.3 Reliability index when k＝2，k＝1 and k＝1／2

3 验证分析

以表1所示参数为例，分别对贮箱椭球下底、圆柱筒及椭球上底的时变可靠性进行分析，并与服从正态分布的应力-强度干涉可靠性方法及区间可靠性方法进行对比分析，验证本文方法的有效性。

不确定载荷应力区间可根据外界随机载荷参数而求得，假设不确定载荷应力区间Su（Y，t）为［0，10］，则据式（22）～式（25）可得贮箱应力区间参数，如表2所示。

服从正态分布的应力-强度干涉可靠性方法是一种常用的概率可靠性分析方法，在参数具体

表1 贮箱示例参数Tab le 1 Sam p le param eters of tank

表2 贮箱应力区间参数Tab le 2 Param eters of tank stress interval MPa

式中：Φ（·）为标准正态分布函数。

区间可靠性方法是一种重要的非概率可靠性分析方法，但其对非完全可靠状态的分析过于保守［19］，任意时刻区间可靠性指标ηi可表示为

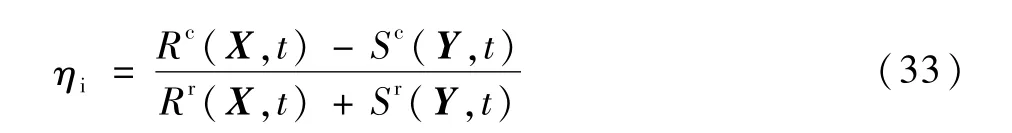
据式（30）～式（33），可得贮箱椭球下底、圆柱筒及椭球上底的可靠性指标ηi、ηn及η，如图4所示。

如图4（a）所示，当0 h≤t≤44 230 h时，存在ηn＝1、1.908≥ηi≥1及1.418≥η≥1，贮箱椭球下底处于完全可靠状态；当44 230 h＜t≤T时，存在1＞ηn≥0.992、1＞η≥0.908及1＞ηi≥0.572，贮箱椭球下底处于非完全可靠状态。

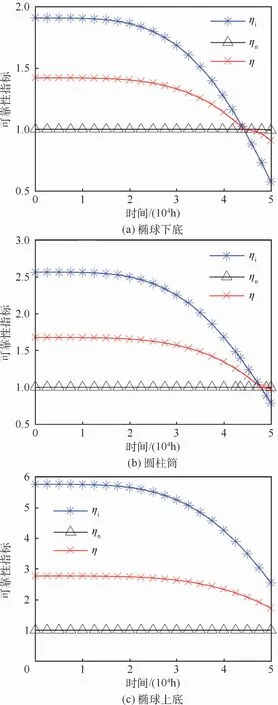
图4 贮箱椭球下底、圆柱筒和椭球上底可靠性指标Fig.4 Reliability indexes of ellipsoid roof，cylinder and ellipsoid bottom

如图4（b）所示，当0 h≤t≤47 830 h时，存在ηn＝1、2.566≥ηi≥1及1.676≥η≥1，贮箱圆柱筒处于完全可靠状态；当47 830 h＜t≤T时，存在1＞ηn≥0.999、1＞ηi≥0.788及1＞η≥0.977，贮箱圆柱筒处于非完全可靠状态。

如图4（c）所示，当0 h≤t≤T时，存在ηn＝1、5.762≥ηi≥2.537及2.765≥η≥1.716，贮箱椭球上底处于完全可靠状态。

综上所述，本文方法的分析结果与服从正态分布的应力-强度干涉可靠性方法及区间可靠性方法分析结果一致，η介于ηn与ηi之间。当椭球下底、圆柱筒及椭球上底处于完全可靠状态时，可靠性指标ηn＝1、ηi≥1及ηn≤η≤ηi，η表示其安全裕度。当椭球下底、圆柱筒及椭球上底处于非完全可靠状态时，可靠性指标0＜ηn＜1、0＜ηi＜1及ηi＜η＜ηn，η表示其可靠度。区间干涉时变可靠性分析方法无须参数的具体分布即可对贮箱的可靠性进行分析，且可有效改善区间可靠性方法对非完全可靠状态分析过于保守的问题。