可重复使用飞行器再入姿态的区间二型自适应模糊滑模控制设计
2020-06-01杨珍书毛奇窦立谦
杨珍书,毛奇,窦立谦
(1.江苏航空职业技术学院 航空工程学院 镇江市无人机应用创新重点实验室,镇江212134;2.天津大学 电气自动化与信息工程学院,天津300072)
为进一步推动空间应用的深入和空间技术的发展,可重复使用飞行器(Reusable Launch Vehicle,RLV)受到了广泛的关注与研究。作为一类新型的天地往返飞行器,RLV兼具航空器与航天器特点,其在军事和民用领域具有广泛的应用前景[1-2]。作为一类多变量系统,RLV具有较强的非线性和强耦合性,且在再入返回过程中易受飞行环境和飞行范围的影响,由此对可重复运载器控制系统设计产生了极大的挑战[3-4]。
为了保证RLV安全且可靠的再入飞行,国内外学者在近年来进行了非常多的研究工作。Groves等[5]基于飞行器的线性化模型,设计了线性二次型调节器控制方法。但由于飞行器模型具有较大的非线性,线性化后的模型与飞行器自身模型存在一定的建模误差。Georgie和Valasek[6]针对再入飞行器提出了非线性动态逆姿态控制策略。然而,当模型存在较大不确定时,此控制策略不能实现非线性项的对消,进而影响飞行器控制性能。Fiorentini等[7]利用反步方法思想针对飞行器设计了非线性鲁棒控制器,但在计算过程中,由于虚拟控制指令被多次求导,易产生微分膨胀问题,从而无法保证飞行器跟踪性能。文献[8-10]针对飞行器模型特点,利用鲁棒自适应控制技术分别设计了控制器,取得了较好的控制效果。
然而,由于RLV在再入飞行阶段动力学参数变化较大,易受到模型参数不确定性和外界干扰的影响,同时飞行器再入模型在转化过程中存在未建模动态项,因此所设计的再入RLV控制策略要具有较强鲁棒性。滑模控制(Sliding Mode Control,SMC)方法是一类具有较强鲁棒性的控制方法,常用于飞行器控制策略的构建。Shtessel等[11-12]针对RLV,基于内外双环结构提出了滑模控制器,进而避免了对姿态角误差的高阶求导问题。Liu等[13]结合状态扩张观测器设计滑模控制策略,取得了良好的跟踪性能。模糊逻辑系统(Fuzzy Logic System,FLS)由于能较好地处理模型不确定性和非线性项问题,因此受到了众多学者关注[14-17]。相比于type-1模糊系统,type-2模糊系统能在Mamdani和Takagi-Sugeno FLS中提供额外的自由度[18-21],尤其是在系统存在大量不确定性的情况下能够提供更好的跟踪逼近性能。Tao等[22]针对飞行器存在测量噪声问题,利用type-2模糊系统设计控制器,使得系统具有较好的跟踪控制性能。
对此,本文考虑RLV在参数不确定性和外界干扰影响下系统姿态跟踪问题,结合区间二型自适应模糊系统和滑模控制技术设计RLV再入姿态跟踪控制策略。首先,基于RLV再入动态模型和反步策略,将飞行器姿态模型分为内外环子系统。接着,将RLV再入动态模型的参数不确定性和外界干扰分别看作内外环子系统非线性项的一部分。然后,设计合适的区间二型模糊系统用于子系统非线性项的估计。同时,利用滑模控制策略和自适应技术构造飞行器的外环子系统的虚拟控制量,进而确定内环子系统的控制律。在姿态角控制策略设计中,引入一阶低通滤波器以处理虚拟控制量。基于Lyapunov方法在理论上证明闭环控制系统的稳定性,且RLV姿态跟踪误差能收敛在原点附近的小邻域中。最后,通过RLV六自由度模型的数值仿真验证了本文所提出控制方法的有效性及跟踪性能。
1 问题描述
1.1 RLV再入动态模型
RLV再入飞行动态过程可由三自由度质心运动的平动方程与三自由度绕质心运动的转动方程完整描述。考虑飞行器在再入过程为无动力飞行(总是正确的),RLV姿态运动方程可以描述为
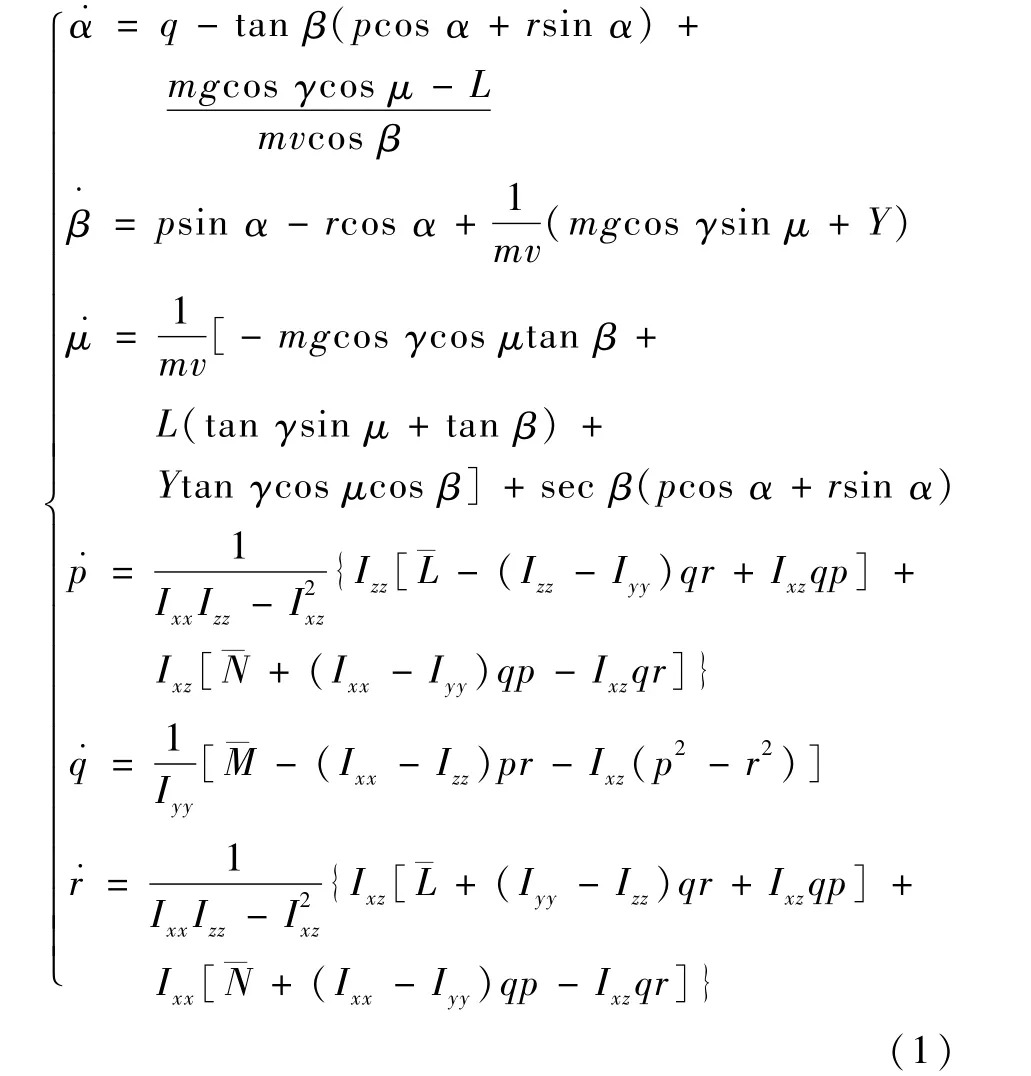
式中:α为飞行器的迎角;β为侧滑角;μ为倾侧角;p为滚转角速率;q为俯仰角速率;r为偏航角速率;¯L为滚转通道控制力矩;¯M为俯仰通道控制力矩;¯N为偏航通道控制力矩;γ为航迹角;m为飞行器质量;v为飞行速度;L为气动升力;Y为侧向力;Ixx、Iyy、Izz、Ixz为飞行器的转动惯量;g为重力加速度。
注1 本文RLV再入动态模型是基于如下假设[1,16]建立的:
假设1 在再入飞行阶段,地球自转速率对飞行器的影响可忽略不计。
假设2 地球大气层视为静止的,且其质量变化忽略不计。
1.2 姿态控制模型
RLV再入动态模型具有多变量耦合、强非线性等特点,使得再入姿态跟制器的设计变得复杂。为便于设计RLV再入姿态控制器,将飞行器模型式(1)转化为如下形式姿态控制模型:

式中:Ω=[α,β,μ]T为飞行器姿态角向量;w=[p,q,r]T为飞行器姿态角速率向量;u=[¯L,¯M,¯N]T为控制输入向量;y=Ω 为输出向量;ΔF=[ΔF1,ΔF2,ΔF3]T为飞行器气动参数摄动引起的参数不确定性项;ΔD=[ΔD1,ΔD2,ΔD3]T为系统外 界 干 扰 综 合 项,ΔD =I-1(ΔD0-ΔI˙w-MΔIw),I和M 为矩阵(其具体表达式在下文给出),ΔI为参数不确定性,ΔD0为外界干扰;FΩ=


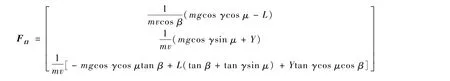

注2 考虑RLV的背景意义和实际飞行情形,假设3和假设4总是合理的。在实际再入姿态控制中,飞行器函数矩阵的上下界并不需要确定得到。同时,假设3和假设4确保了系统函数矩阵的非奇异性。
本文旨在针对RLV再入动态模型式(1)和式(2),给定任意满足假设3的期望指令信号,设计合理的再入姿态控制律,使得RLV能跟踪期望指令信号,且飞行器闭环控制系统的稳定性及姿态跟踪误差的有界性能得以保证。
2 RLV再入姿态控制策略
2.1 区间二型模糊系统
利用单值模糊器、乘积推理机及中心集降阶器,可得到区间一型模糊集输出,该输出可由2个端点yl、yr表示。通过计算和的均值,去模糊化区间集,得到去模糊化的清晰输出为

2.2 再入姿态控制器设计
步骤1 外环姿态角控制器。
定义姿态角跟踪误差为eΩ=Ω-Ωd∈R3×1,其中Ωd=[αd,βd,μd]T为系统给定姿态角跟踪信号,且其导数Ω·d有界。
由飞行器姿态控制模型式(2),得到RLV姿态角跟踪误差动态为
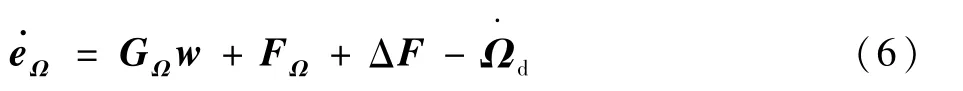
定义姿态角子系统的滑模面为SΩ=DΩeΩ=DΩ(Ω-Ωd),则


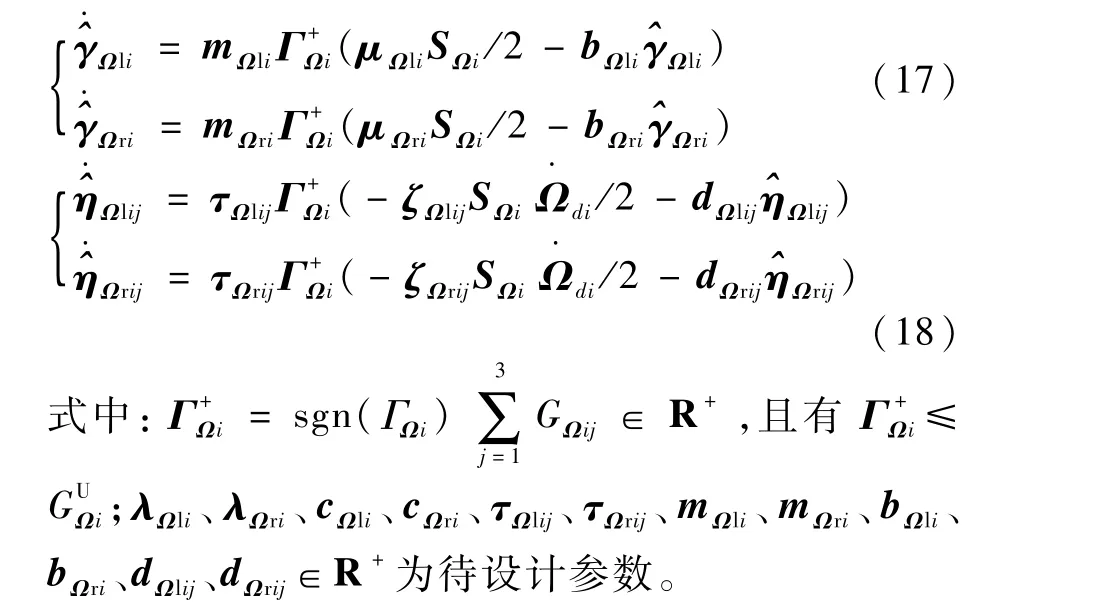
步骤2 内环姿态角速率控制器。
现设计虚拟控制输入wd。定义姿态角速率跟踪误差ew=w-wd∈R3×1,其中wd=[pd,qd,rd]T为期望姿态角速率跟踪信号,且其导数˙wd有界。
基于飞行器控制模型式(2),姿态角速率的跟踪误差方程可表示为

类似地,定义姿态角速率子系统滑模面为Sw=Dwew=Dw(w-wd),可得滑模面动态为


3 稳定性分析
定理1 对于飞行器控制模型式(2),且满足假设3、假设4和引理1,飞行器姿态角和姿态角速率子系统的控制律分别设计为式(13)和式(26),并选取参数向量自适应更新律分别为式(16)、式(18)和式(28)、式(30),则RLV闭环控制系统是半全局一致有界稳定的,且飞行器姿态角跟踪误差能收敛于原点附近的一个小邻域内。
证明 选取Lyapunov函数为
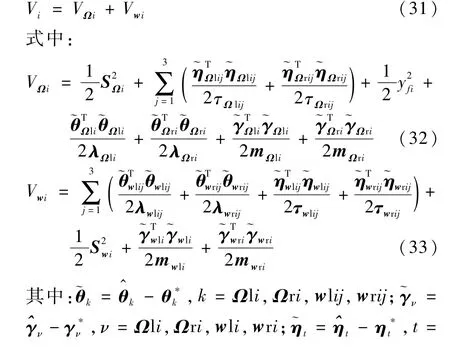


类似地,结合式(28)、式(30)、式(36)和不等式(38)证明,可以得到即

综上,整理式(40)和式(41)可得到
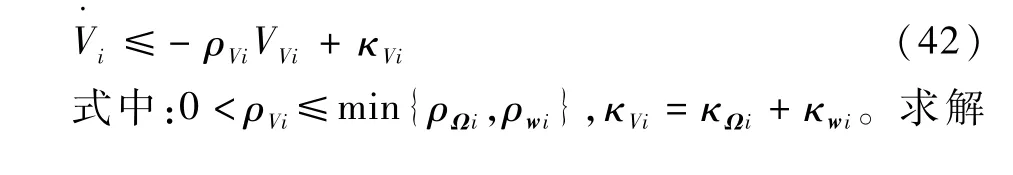
式(42),可得


4 仿真验证
为验证所提控制策略的有效性,应用所提出的控制方法针对RLV再入动态模型进行仿真实验。
4.1 参数设定
再入飞行器转动惯量值分别设定为Ixx=434 270 slug·ft2,,Ixz=17 880 slug· ft2,Iyy=961 200 slug·ft2和Izz=1 131 541 slug·ft2,1 ft=0.304 8m,1 slug·ft2=14.593 9 kg·m2。飞行器其他初始条件如表1所示。
仿真中,选取以高斯型隶属度函数为主设计的区间二型模糊系统。飞行器控制器待设计参数分别设置如下:KΩ1=diag(1,0.8,1),Kw1=18I3×3,KΩ2=diag(1.6,1.4.1.6),Kw2=15I3×3,Kf=0.1I3×3;λΩ1=λΩr=cΩl=cΩr=[1.5,1.2,1.5]T,λwl=λwr=cwl=cwr=[1,1,1;1,1,1;1,1,1],δ=0.001[1,1,1]T;mΩl=mΩr=bΩl=bΩr=[1,1,1.2]T,mwl=mwr=bwl=bwr=[1.1,1,0.9],τΩl=τΩr=dΩl=dΩr=[1.4,1.4,1.2;1.4,1.4,1.2;1.4,1.4,1.2],τwl=τwr=dwl=dwr=[1.2,1.2,1.2;1.2,1.2,1.2;1.2,1.2,1.2]。
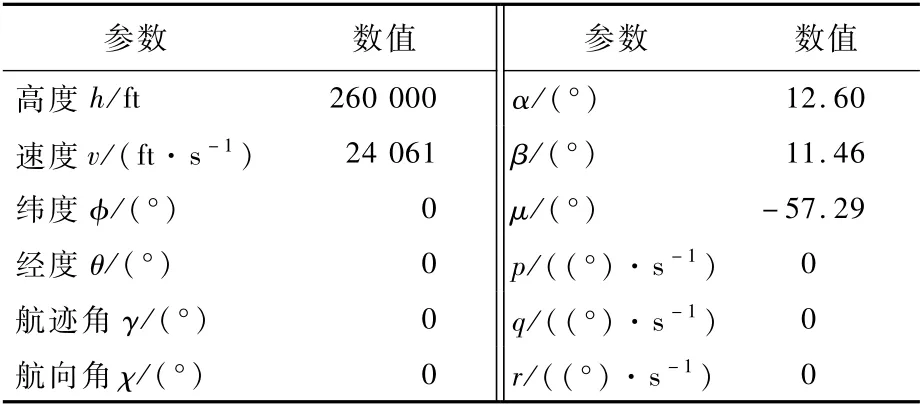
表1 再入RLV初始参数值Tab le 1 Initial param eter values of reentry RLV
此外,为验证RLV再入姿态控制器的鲁棒性能,针对飞行器控制模型式(2)加入参数不确定性ΔF=0.1FΩ和外界干扰为
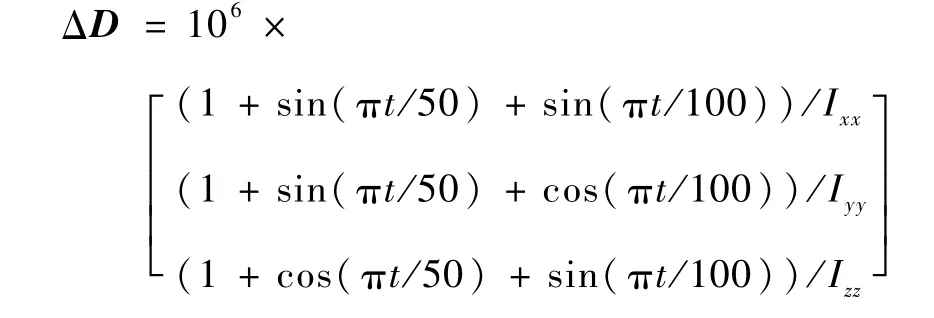
4.2 仿真分析
为了更好地验证本文所设计姿态控制方法的有效性及跟踪性能,在同样的条件(模型和初始情况)下与传统的滑模控制方法进行仿真实验对比。仿真结果如图1~图4所示。
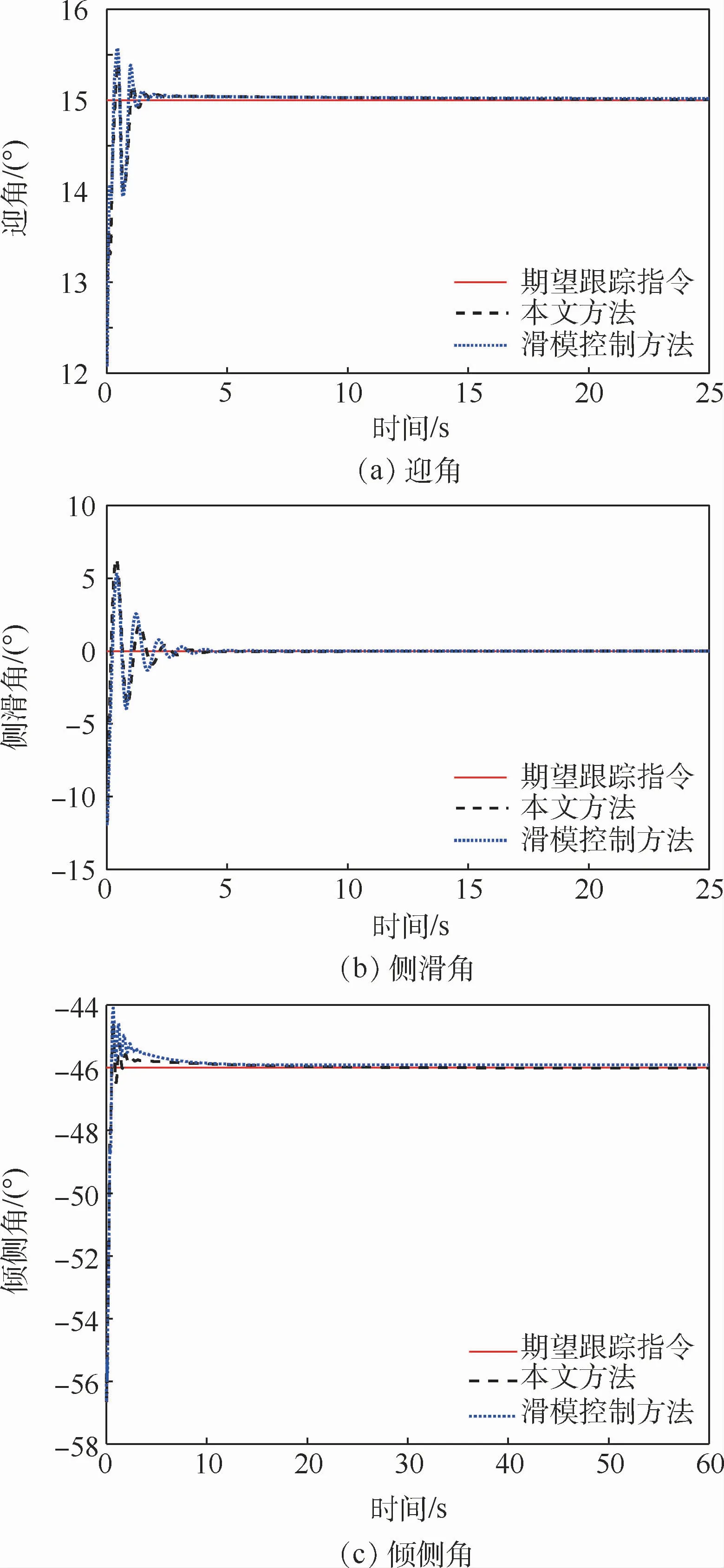
图1 姿态角跟踪响应曲线Fig.1 Attitude angle tracking response curves
图1为迎角、侧滑角和倾侧角跟踪曲线。由图1可以看出,在飞行器模型的参数不确定性和外界干扰的综合影响下,所提出的姿态控制策略能使得再入RLV在很短时间(约2 s)内实现对期望指令的稳定跟踪,且其稳定跟踪时间快于传统滑模控制方法。
图2为迎角、侧滑角和倾侧角跟踪误差变化曲线。图2表明,所提出的控制策略能够以更高的精度对期望指令信号进行跟踪。
图3为滚转角、俯仰角和偏航角速率变化曲线。由图3可知,在所设计控制器作用下,再入飞行器三通道角速率的变化更加平滑。
图4为飞行器的滚转、俯仰和偏航三通道所需力矩响应曲线。由图4可知,相比于传统的滑模控制方法,RLV在所提出的姿态跟踪策略下能产生更加平滑的控制力矩且无抖振现象。
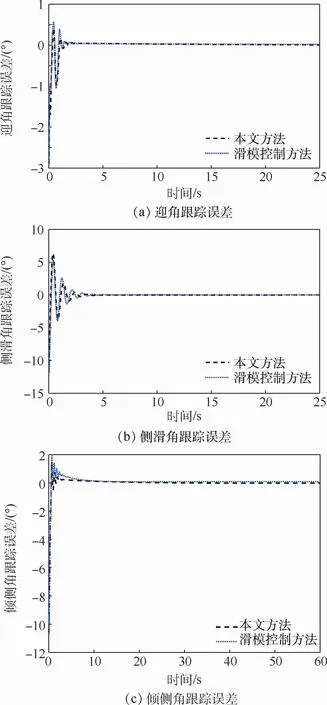
图2 姿态角跟踪误差变化曲线Fig.2 Attitude angle tracking error changing curves
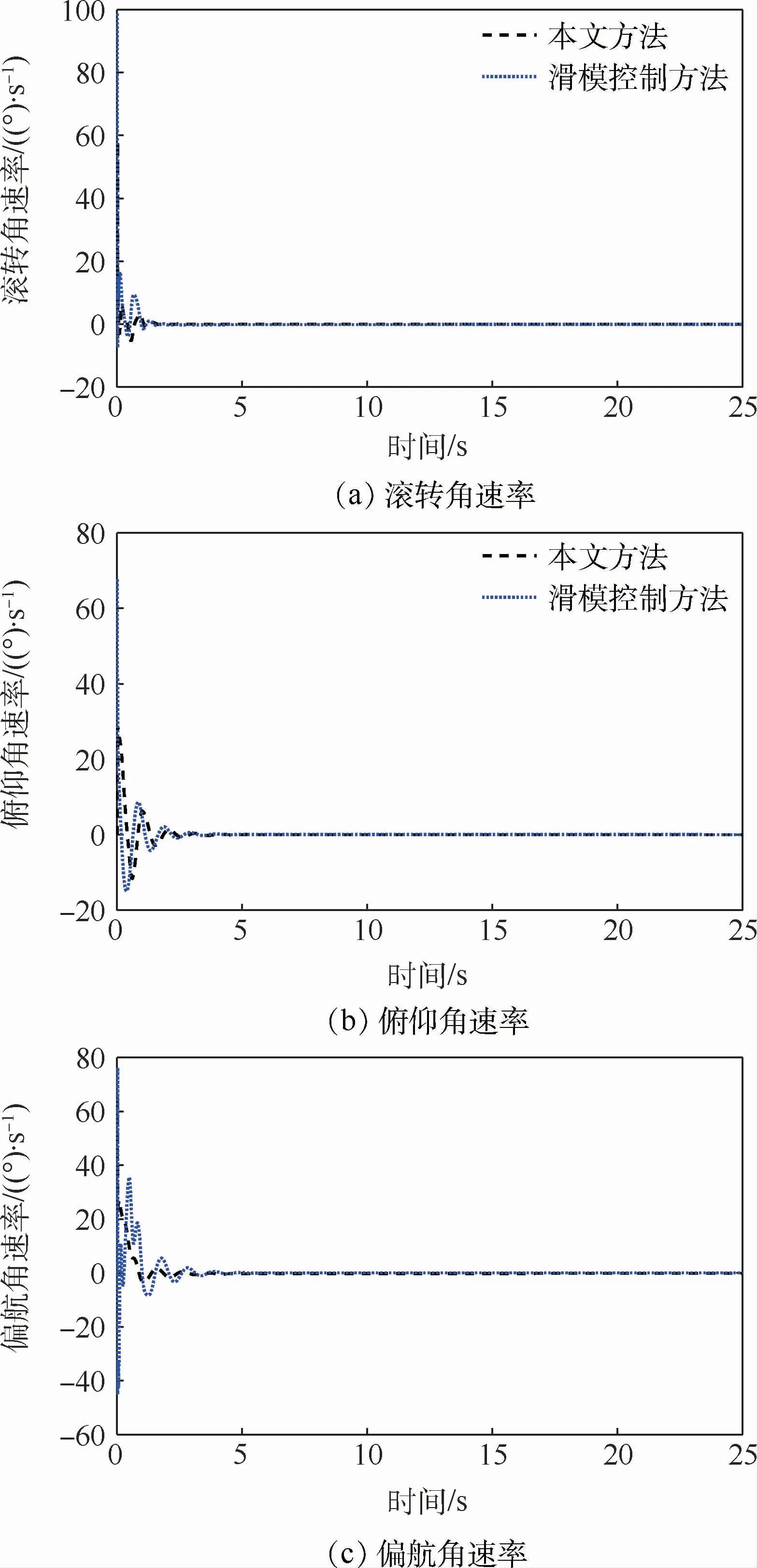
图3 姿态角速率变化曲线Fig.3 Attitude angular rate changing curves
5 结 论
本文针对RLV姿态跟踪控制问题,考虑RLV再入动态模型的参数不确定性和外界干扰情形,基于区间二型自适应模糊技术提出一种再入姿态滑模控制策略。
1)该控制策略引入区间二型模糊系统对飞行器姿态角和角速率子系统非线性项进行逼近,有效地解决了RLV再入动态模型的强非线性问题。
2)结合滑模控制方法及自适应更新律设计,使得所设计控制器具有较强的鲁棒性。同时,利用Lyapunov方法在理论上严格证明了RLV闭环控制系统的稳定性。
3)通过对飞行器再入模型的仿真对比验证,所设计的再入姿态控制器在RLV再入动态模型参数不确定性和外界干扰的影响下,能够有效地实现对期望指令信号稳定且快速地跟踪,且相比于传统滑模控制方法具有更好的跟踪控制性能。
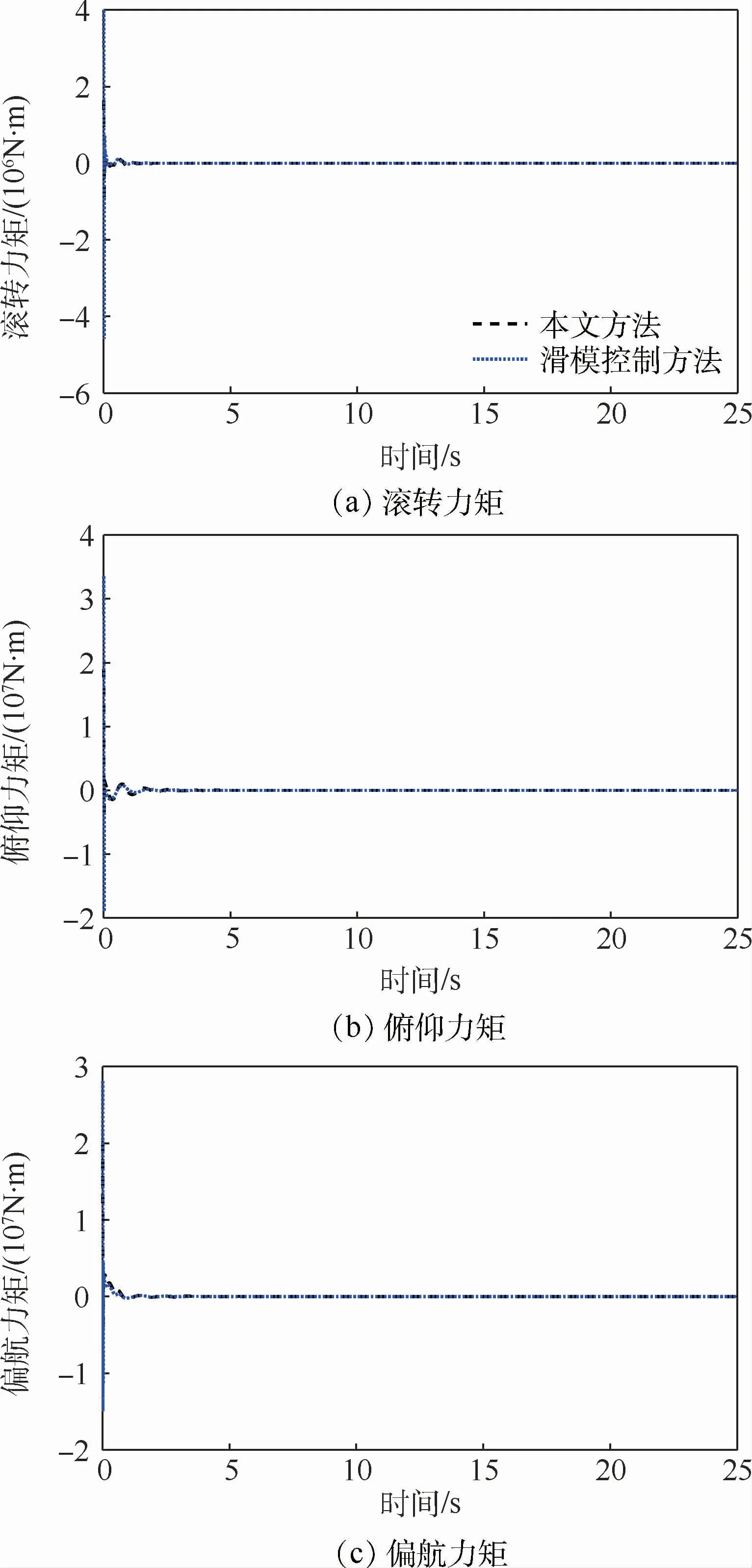
图4 RLV力矩响应曲线Fig.4 Torque response curves of RLV
