考虑壁面效应的摆动翼推进特性数值模拟

2020-05-31李永成陈纪军

船舶与海洋工程 2020年2期

李永成，王健，陈纪军

（中国船舶科学研究中心, 江苏无锡 214082）

0 引言

自然界中的很多生物经过亿万年的进化以后，具备了较强的运动能力，如快速性、操纵性和推进性能等。空中飞行的鸟类和水中游动的鱼类很有代表性，其快捷、高效的运动特性主要源于其附体（翼或尾巴）的摆动运动[1]。鉴于此，国内外专家学者开展了大量以海洋生物胸鳍和尾鳍为原型的仿生摆动翼推进特性研究。例如：PETRO等[2]采用任意拉格朗日-欧拉方法对不同运动参数下的二维摆动水翼进行数值模拟研究，提出一个无量纲参数，用于衡量摆动翼的推进效率；PAN等[3]通过在摆动翼的上游布置振荡D型圆柱，采用数值模拟方法模拟复杂流场下摆动翼的推进特性，计算结果表明，相位差的改变会对后置摆动翼的推进效率产生极大的影响，且存在最优相位差对应最大推进效率。

上述研究主要集中在摆动翼推进特性水动力学分析方面，且流场均为无界流场，未考虑有限流场中摆动翼推进特性的差异。事实上，在自然界中，无论是空中飞行的鸟类还是水中游动的鱼类，其附体（翅膀或鱼尾）的摆动运动都不是独立完成的，都与自身的主体结构相连接或相接近。因此，很有必要研究壁面效应对摆动翼推进特性的影响。

本文主要基于重叠网格技术对考虑壁面效应的摆动翼的推进特性进行数值模拟研究，从机理上阐述海洋生物游动的高机动性和高效性，以便于设计出具有优越的推进性能、机动性能和低噪声特性的仿生摆动翼，为新型自主式水下潜器（Autonomous Underwater Vehicle, AUV）的研发提供一定的参考。

1 计算模型和运动方程

本文选取二维的NACA0012翼型作为计算模型，弦长为0.1m，记为特征长度C。水翼放置在2个平行的壁面中间，水翼中心线与下壁面之间的距离设为d。相应的边界条件设置为：入口和上边界设置为速度入口边界条件；出口设置为无回流边界条件；下边界设置为壁面条件。图1为计算模型和边界条件。

水翼以其弦向最大厚度处（距离头部约1/4弦长）为中心作俯仰摆动运动，运动方程为

式(1)中：θ0为摆动运动幅值；f为摆动频率；t为时间。

2 数值模拟方法及其精度验证

本文所述水翼摆动运动问题属于典型的黏性不可压缩流场求解问题，因此需求解N-S方程。控制方程为

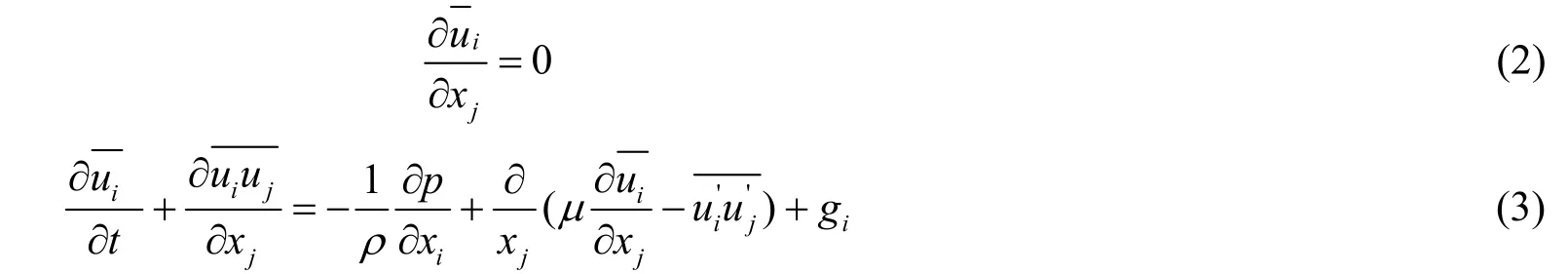
式(2)和式(3)中：xi和xj分别为坐标系的水平方向和垂直方向；ui和uj分别为水平方向和垂直方向的速度分量；分别为水平方向和垂直方向的时均速度分量；ρ为流体密度；μ为分子黏性系数；gi为外部体积力在xi方向上的分量；t为时间；p为时均压力；为脉动速度分量；为雷诺应力张量。

本文采用重叠网格技术对水翼的摆动运动进行数值模拟。重叠网格技术的优势在于能避免网格的重新生成，能解除对摆动翼大幅度运动的限制[4]。本文主要借助商业软件ANSYS Fluent中的重叠网格功能采用2套网格对摆动翼的流场进行数值模拟。为保证数值计算的精度，均采用结构化网格进行计算。取水翼弦长C为特征长度，二维计算区域的大小为40C× 25C。水翼周围第一层网格的高度为1（即y+= 1），确保第一层网格位于黏性底层区域。在经过网格无关性验证之后，选取的重叠网格与背景网格组合，此时网格数量约为12万个。该数值模拟方法的精度验证可参考文献[5]。

3 结果与讨论

下面针对摆动翼模型，采用商业软件ANSYS Fluent 对不同壁面距离下的摆动翼的流场进行数值模拟，并系统地考察摆动翼的各运动参数对推进特性的影响。由于本文研究的摆动翼无垂向的升沉运动，因此传统的无量纲频率斯特哈尔数无法引入，这里重新定义一个新的无量纲频率*f，用于对摆动翼的推进特性进行分析，其表达式为

式(4)中：f为摆动频率；C为弦长；U0为来流速度。

计算工况见表1，其中：工况1～工况5主要考察俯仰振幅对推进特性的影响；工况6～工况10主要考察无量纲频率对推进特性的影响。

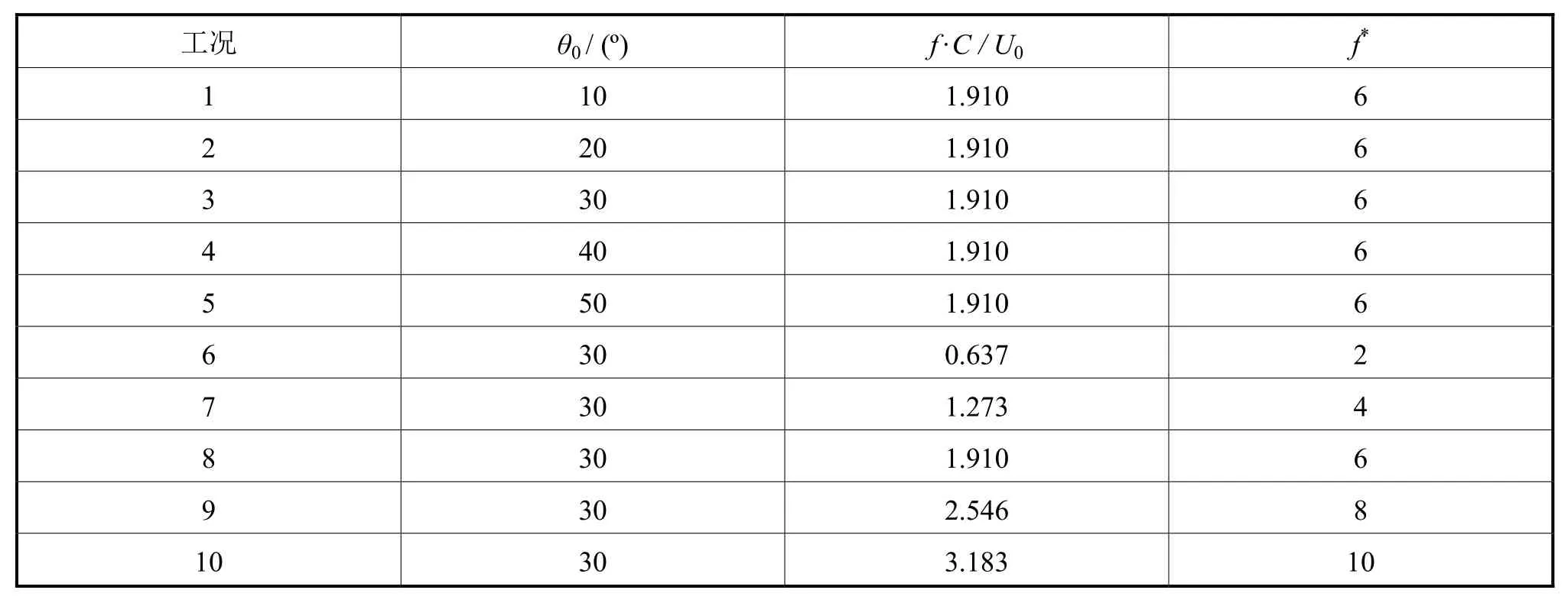
表1 计算工况

在正式计算之前，首先确定一个边界壁面距离d∞。当壁面距离d超过该距离时，可认为壁面对摆动翼的影响可忽略，可近似认为摆动翼处于无界流场中。表2为不同壁面距离下摆动翼平均阻力系数值。其他运动参数设置为：θ0= 30°；f= 1.0 Hz。CD-Mean和CL-Mean分别为平均阻力系数和平均升力系数；CD为阻力系数。CD-Mean和CL-Mean的表达式为

式(5)和式(6)中：D和L分别为摆动翼在水平方向和垂直方向上受到的阻力和升力；ρ为水的密度；v为来流速度；C为摆动翼的弦长。

表2 不同壁面距离下摆动翼平均阻力系数值

从表2中可看出：随着壁面距离的增大，摆动翼平均阻力系数值逐渐趋于平稳；当壁面距离大于2.0C之后，对应的CD-Mean不再发生变化。因此，可认为边界壁面距离d∞= 2.0C。在接下来的计算中，可认为当壁面距离等于2.0C时，摆动翼处于无界流场中。

图2 摆动翼升力系数和阻力系数随时间的变化曲线

图2为摆动翼升力系数和阻力系数随时间的变化曲线。由图2可知，摆动翼的升力系数和阻力系数均随时间呈周期性变化，且阻力系数的变化周期为摆动翼运动周期的 1/2，升力系数的变化周期与摆动翼运动周期一致。该结论与毕晓波[6]得到的结论一致，从侧面验证了本文计算方法的可靠性。

3.1 俯仰运动幅值对摆动翼推进特性的影响

图3为不同壁面距离下摆动翼推力系数和推进效率随俯仰振幅的变化曲线，壁面距离的变化范围为 0.5C～2.0C，俯仰振幅的变化范围为θ0= 10°～50°，其他参数保持不变，分别为：推力系数CT和推进效率η的定义为

式(7)和式(8)中：T为摆动翼在水平方向上受到的推力；M(t)为任意时刻摆动翼受到的力矩；v为来流速度。

从图3中可看出：不同壁面距离下摆动翼的推力系数和推进效率随俯仰振幅的变化趋势一致；推力系数先随着俯仰振幅增大到极值，再逐渐减小，且存在最佳俯仰振幅对应最大推力系数。在不同壁面距离下，该最佳俯仰振幅近乎不变，约为 30°；推进效率随着俯仰振幅的增大呈增长趋势，这一结论与文献[7]中的结论一致。

此外，从图3中还可看出：随着壁面距离的减小，摆动翼推力系数和推进效率均呈现出逐渐增大的趋势。不同之处在于：摆动翼产生的推力随壁面距离的逐渐减小而持续增大，即认为壁面距离越小，摆动翼的推力越大；摆动翼的推进效率随壁面距离的不断减小呈现出先增大后减小的趋势，且当d= 0.80C时达到最大值。因此，壁面的存在可有效提高摆动翼的推进特性。

图3 不同壁面距离下摆动翼推力系数和推进效率随俯仰振幅的变化曲线

3.2 无量纲频率 *f对摆动翼推进特性的影响

类似地，给出不同壁面距离下摆动翼推力系数和推进效率随无量纲频率f*的变化曲线（见图 4），壁面距离的变化范围不变，f*的变化范围为 2 ～ 10，θ0=30°。

图4 不同壁面距离下摆动翼推力系数和推进效率随无量纲频率f *的变化曲线

从图4中可看出：在同一壁面距离下，摆动翼的推力系数和推进效率随壁面距离的变化趋势相同；推力系数随着的增加近乎呈线性增大的趋势；推进效率先随增大到极值，再逐渐减小，且存在最佳f*对应最大推进效率；在不同壁面距离下，最佳f*近乎不变，约为0.3。

此外，不同f*下摆动翼的推力系数和推进效率随壁面距离的变化趋势与不同俯仰振幅下的变化趋势类似，即摆动翼产生的推力随着壁面距离的减小呈现出持续增大的规律，而推进效率在d= 0.80C时达到最大值。该结论与第3.1节中的结论相吻合，再次说明当壁面距离为0.80C时，摆动翼可获得最佳推进性能。

3.3 摆动翼周围的流场结构

考虑到摆动翼的推进性能与其周围的流场结构密切相关，对摆动翼周围的流场结构进行展示，从水动力学机理的角度揭示摆动翼可获得良好推进性能的原因。

图5为不同壁面距离下摆动翼流场涡量分布图，相关运动参数设置为：v= 0.1 m/s；θ0=30°；f=1.0 Hz。本文选择Wz涡量判断准则，其表达式为其中u和v分别为摆动翼水平方向和垂直方向的速度分量。

图5 不同壁面距离下摆动翼流场涡量分布图

从图5中可看出：在不同壁面距离下，摆动翼的运动伴随着涡环的形成。具体来说，摆动翼上表面前缘的诱导涡沿着水翼上表面向后运动至尾缘处脱落（相对于摆动翼平衡位置而言，位于中线下方），接着在水翼的头部出现新的脱落涡；同时，水翼下表面的脱落涡沿着水翼下表面向后运动至尾缘处脱落（位于中线上方），如此循环往复。在摆动翼持续运动的同时，上下表面的分离涡脱落，此时摆动翼的尾部流场中形成上下错列分布的涡环。上表面脱落形成的涡环向下方（相对于摆动翼平衡位置而言）流动，顺时针旋转；下表面脱落形成的涡环向上方流动，逆时针旋转。如此，二者之间便形成了典型的反卡门涡街，提供摆动翼前进的动力。

然而，由于底壁面的存在，不同壁面距离下摆动翼的涡流场结构亦存在一定的差别。当壁面距离较大时（d=1.5C），壁面的存在对涡流场的影响较小，近似等于无界流场；随着壁面距离的减小，摆动翼的流场逐渐受到下壁面的影响。摆动翼脱落的涡环逐渐被“压扁”，与壁面之间形成夹角，且壁面距离越小，对应的夹角越小。由于涡环的脱落伴随着能量的释放，且该能量可分解为水平方向的能量和垂直方向的能量，其水平方向的能量与摆动翼的运动方向一致，用于推动摆动翼。涡环夹角越小，意味着水平方向的能量分量越大，摆动翼的推进性能越优。因此，可解释上述计算结果，即壁面距离的存在有助于提高摆动翼的推进特性。